古代インドが数学で世界を変えた5つの方法
(MENAFN - The Conversation) It should come as no surprise that the first recorded use of the number zero, to be made as early as the 3rd or 4th century, happened in India. Mathematics on the Indian subcontinent has a rich history and thrived for centuries before similar advances were made in Europe, with its influence meanwhile spreading to China and the Middle East.
As well as giving us the concept of zero, Indian mathematicians made seminal contributions to the study of . Perhaps most significantly, the decimal system that we still employ worldwide today was first seen in India.
The number system
As far back as 1200 BC, mathematical knowledge was being written down as part of a large body of knowledge known as . In these texts, numbers were commonly expressed as . For example, 365 might be expressed as three hundreds (3x10²), six tens (6x10¹) and five units (5x10⁰), though each power of ten was represented with a name rather than a set of symbols. It is that this representation using powers of ten played a crucial role in the development of the decimal-place value system in India.
Brahmi numerals.
From the , we also have written evidence of the , the precursors to the modern, Indian or Hindu-Arabic numeral system that most of the world uses today. Once zero was introduced, almost all of the mathematical mechanics would be in place to enable ancient Indians to study higher mathematics.
The concept of zero
Zero itself has a much longer history. The , in what is known as the Bakhshali manuscript, were simple placeholders – a tool to distinguish 100 from 10. Similar marks had already been seen in the and arguably in .
But only in India did the placeholder symbol for nothing progress to become a . The advent of the concept of zero allowed numbers to be written efficiently and reliably. In turn, this allowed for effective record-keeping that meant important financial calculations could be checked retroactively, ensuring the honest actions of all involved. Zero was a significant step on the route to the .
No abacus needed. Shutterstock
These accessible mechanical tools for working with mathematical concepts, in combination with a strong and open scholastic and scientific culture, meant that, by around 600AD, all the ingredients were in place for an explosion of mathematical discoveries in India. In comparison, these sorts of tools were not popularised in the West until the early 13th century, though .
Solutions of quadratic equations
In the seventh century, the first written evidence of the rules for working with zero were formalised in the . In his seminal text, the astronomer introduced rules for solving quadratic equations (so beloved of secondary school mathematics students) and for computing square roots.
Rules for negative numbers
Brahmagupta also demonstrated rules for working with negative numbers. He referred to . He wrote down rules that have been interpreted by translators as: 'A fortune subtracted from zero is a debt,' and 'a debt subtracted from zero is a fortune'.
This latter statement is the same as the rule we learn in school, that if you subtract a negative number, it is the same as adding a positive number. Brahmagupta also knew that 'The product of a debt and a fortune is a debt' – a positive number multiplied by a negative is a negative.
Negative cows. Shutterstock
For the large part, European mathematicians were reluctant to accept negative numbers as meaningful. Many took the view that . They reasoned that numbers were developed for counting and questioned what you could count with negative numbers. Indian and Chinese mathematicians recognised early on that one answer to this question was debts.
For example, in a primitive farming context, if one farmer owes another farmer 7 cows, then effectively the first farmer has -7 cows. If the first farmer goes out to buy some animals to repay his debt, he has to buy 7 cows and give them to the second farmer in order to bring his cow tally back to 0. From then on, every cow he buys goes to his positive total.
Basis for calculus
This reluctance to adopt negative numbers, and indeed zero, held European mathematics back for many years. Gottfried Wilhelm Leibniz was one of the first Europeans to use zero and the negatives in a systematic way in his in the late 17th century. Calculus is used to measure rates of changes and is important in almost every branch of science, notably underpinning many key discoveries in modern physics.
Leibniz: Beaten to it by 500 years.
But had already discovered many of Leibniz's ideas . Bhāskara, also made major contributions to algebra, arithmetic, geometry and trigonometry. He provided many results, for example on the solutions of certain 'Doiphantine' equations, that .
, founded by in the 1300s, was responsible for many firsts in mathematics, including the use of mathematical induction and some early calculus-related results. Although no systematic rules for calculus were developed by the Kerala school, its proponents first conceived of many of the results that would including Taylor series expansions, infinitessimals and differentiation.
The leap, made in India, that transformed zero from a simple placeholder to a number in its own right indicates the mathematically enlightened culture that was flourishing on the subcontinent at a time when Europe was stuck in the dark ages. Although its reputation , the subcontinent has a strong mathematical heritage, which it continues into the 21st century by .
とても興味深く読みました:
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 380: What is the zero?\\
(2017.8.21)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
}
\date{\today}
\maketitle
\section{What is the zero?}
The zero $0$ as the complex number or real number is given clearly by the axions by the complex number field and real number field.
For this fundamental idea, we should consider the {\bf Yamada field} containing the division by zero. The Yamada field and the division by zero calculus will arrange our mathematics, beautifully and completely; this will be our natural and complete mathematics.
\medskip
\section{ Double natures of the zero $z=0$}
The zero point $z=0$ represents the double natures; one is the origin at the starting point and another one is a representation of the point at infinity. One typical and simple example is given by $e^0 = 1,0$, two values. {\bf God loves two}.
\section{Standard value}
\medskip
The zero is a center and stand point (or bases, a standard value) of the coordinates - here we will consider our situation on the complex or real 2 dimensional spaces. By stereographic
projection mapping or the Yamada field, the point at infinity $1/0$ is represented by zero. The origin of the coordinates and the point at infinity correspond each other.
As the standard value, for the point $\omega_n = \exp \left(\frac{\pi}{n}i\right)$ on the unit circle $|z|=1$ on the complex $z$-plane is, for $n = 0$:
\begin{equation}
\omega_0 = \exp \left(\frac{\pi}{0}i\right)=1, \quad \frac{\pi}{0} =0.
\end{equation}
For the mean value
$$
M_n = \frac{x_1 + x_2 +... + x_n}{n},
$$
we have
$$
M_0 = 0 = \frac{0}{0}.
$$
\medskip
\section{ Fruitful world}
\medskip
For example, for very and very general partial differential equations, if the coefficients or terms are zero, then we have some simple differential equations and the extreme case is all the terms are zero; that is, we have trivial equations $0=0$; then its solution is zero. When we consider the converse, we see that the zero world is a fruitful one and it means some vanishing world. Recall Yamane phenomena (\cite{kmsy}), the vanishing result is very simple zero, however, it is the result from some fruitful world. Sometimes, zero means void or nothing world, however, it will show {\bf some changes} as in the Yamane phenomena.
\section{From $0$ to $0$; $0$ means all and all are $0$}
\medskip
As we see from our life figure (\cite{osm}), a story starts from the zero and ends with the zero. This will mean that $0$ means all and all are $0$. The zero is a {\bf mother} or an {\bf origin} of all.
\medskip
\section{ Impossibility}
\medskip
As the solution of the simplest equation
\begin{equation}
ax =b
\end{equation}
we have $x=0$ for $a=0, b\ne 0$ as the standard value, or the Moore-Penrose generalized inverse. This will mean in a sense, the solution does not exist; to solve the equation (6.1) is impossible.
We saw for different parallel lines or different parallel planes, their common points are the origin. Certainly they have the common points of the point at infinity and the point at infinity is represented by zero. However, we can understand also that they have no solutions, no common points, because the point at infinity is an ideal point.
Of course. we can consider the equation (6.1) even the case $a=b=0$ and then we have the solution $x=0$ as we stated.
We will consider the simple differential equation
\begin{equation}
m\frac{d^2x}{dt^2} =0, m\frac{d^2y}{dt^2} =-mg
\end{equation}
with the initial conditions, at $t =0$
\begin{equation}
\frac{dx}{dt} = v_0 \cos \alpha , \frac{d^2x}{dt^2} = \frac{d^2y}{dt^2}=0.
\end{equation}
Then, the highest high $h$, arriving time $t$, the distance $d$ from the starting point at the origin to the point $y(2t) =0$ are given by
\begin{equation}
h = \frac{v_0 \sin^2 \alpha}{2g}, d= \frac{v_0\sin \alpha}{g}
\end{equation}
and
\begin{equation}
t= \frac{v_0 \sin \alpha}{g}.
\end{equation}
For the case $g=0$, we have $h=d =t=0$. We considered the case that they are the infinity; however, our mathematics means zero, which shows impossibility.
These phenomena were looked many cases on the universe; it seems that {\bf God does not like the infinity}.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msy}
H. Michiwaki, S. Saitoh, and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{ms}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$, Advances in Linear Algebra
\& Matrix Theory, 6 (2016), 51-58. http://dx.doi.org/10.4236/alamt.2016.62007 http://www.scirp.org/journal/alamt
\bibitem{mos}
H. Michiwaki, H. Okumura, and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces.
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), 1(2017), 70-77.
\bibitem{romig}
H. G. Romig, Discussions: Early History of Division by Zero,
American Mathematical Monthly, Vol. 31, No. 8. (Oct., 1924), pp. 387-389.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182 (Springer).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\bibitem{ann179}
Announcement 179 (2014.8.30): Division by zero is clear as z/0=0 and it is fundamental in mathematics.
\bibitem{ann185}
Announcement 185 (2014.10.22): The importance of the division by zero $z/0=0$.
\bibitem{ann237}
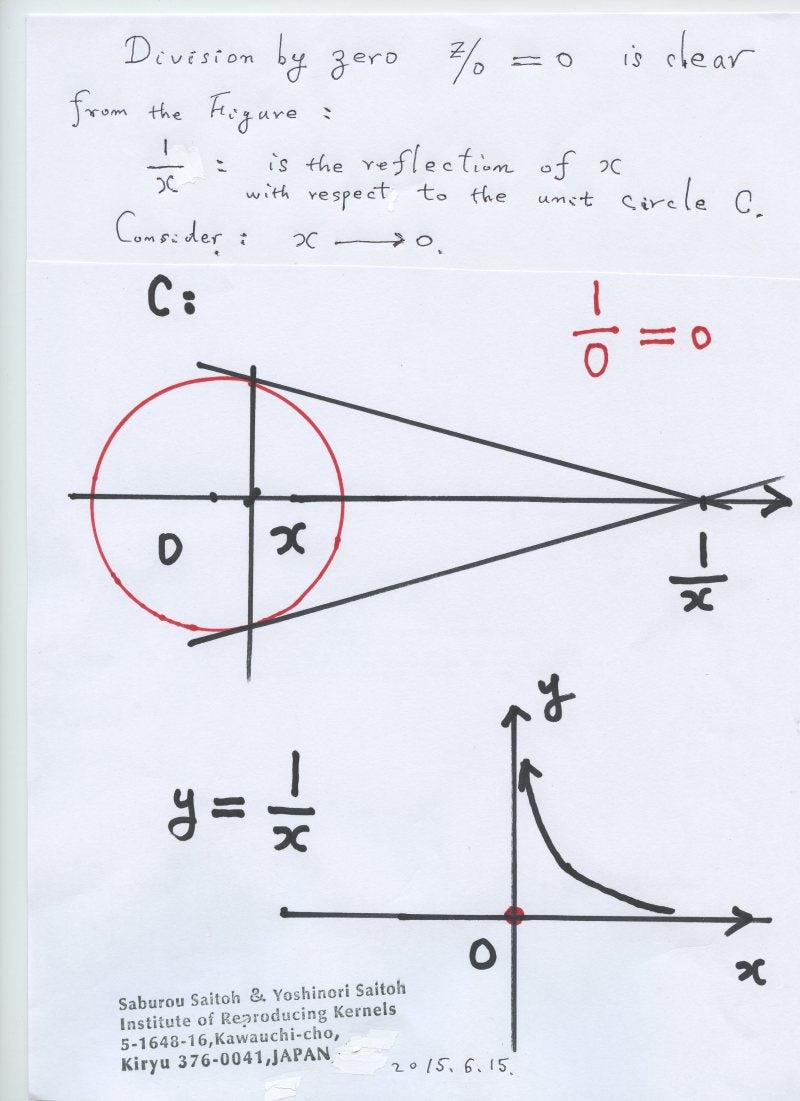
Announcement 237 (2015.6.18): A reality of the division by zero $z/0=0$ by geometrical optics.
\bibitem{ann246}
Announcement 246 (2015.9.17): An interpretation of the division by zero $1/0=0$ by the gradients of lines.
\bibitem{ann247}
Announcement 247 (2015.9.22): The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$.
\bibitem{ann250}
Announcement 250 (2015.10.20): What are numbers? - the Yamada field containing the division by zero $z/0=0$.
\bibitem{ann252}
Announcement 252 (2015.11.1): Circles and
curvature - an interpretation by Mr.
Hiroshi Michiwaki of the division by
zero $r/0 = 0$.
\bibitem{ann281}
Announcement 281 (2016.2.1): The importance of the division by zero $z/0=0$.
\bibitem{ann282}
Announcement 282 (2016.2.2): The Division by Zero $z/0=0$ on the Second Birthday.
\bibitem{ann293}
Announcement 293 (2016.3.27): Parallel lines on the Euclidean plane from the viewpoint of division by zero 1/0=0.
\bibitem{ann300}
Announcement 300 (2016.05.22): New challenges on the division by zero z/0=0.
\bibitem{ann326}
Announcement 326 (2016.10.17): The division by zero z/0=0 - its impact to human beings through education and research.
\bibitem{ann352}
Announcement 352(2017.2.2): On the third birthday of the division by zero z/0=0.
\bibitem{ann354}
Announcement 354(2017.2.8): What are $n = 2,1,0$ regular polygons inscribed in a disc? -- relations of $0$ and infinity.
\bibitem{362}
Announcement 362(2017.5.5): Discovery of the division by zero as
$0/0=1/0=z/0=0$.
\end{thebibliography}
\end{document}
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1
-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi
http://okmr.yamatoblog.net/
Relations of 0 and infinity
Hiroshi Okumura, Saburou Saitoh and Tsutomu Matsuura:
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…
https://sites.google.com/site/sandrapinelas/icddea-2017
2017.8.21.06:37






















































































0 件のコメント:
コメントを投稿