蔡论意谈数学与艺术
作者:蔡论意/翻译:蒋迅

蔡论意和他的画室
译者注:蔡论意先生是一位为了追求绘画艺术而学数学的美国华裔学者。我和王淑红教授在《数学都知道》第一册第九章里专门介绍了他的事迹。现在这里是他的访谈。图片均来自他的个人网站。
1. 什么是你的第一个数学经验?
我的第一个数学经验是象婴儿那样的爬行。这是我们每个人开始了解如何接近的概念。就是说,经过一系列有限的运动序列去达到的是近的概念。而象月亮,不能以这样的方式取得的东西是远的概念。庞加莱在“科学与假设”中谈过这一点。这样的早期现实映射现在还继续在我们大家中继续著。而我们没有意识到我们在不断地映射现实的原因是,它已成为完全自动的,因此没有意识到。我把这个映射过程作为艺术尝试是一个抽象的过程。
但首先,最根本的的数学经验是时间的经验。序列自然地产生于这个最基本的经验。每一刻,似乎被另一个时刻所取代;我们看到每一个逝去的一刻,同时看到新时刻的产生。但是,这个对时间的经验也有一个连续的质量,这使我们得到了富有成果的概念─ 极限。
但是让我用一个更加标准的的方式回答这个问题。我第一次对数学产生深刻印象是当我10或11岁时在纽约市的联合国际学校 (United Nations International School) Chesnay夫人的课上。我记得学的是素数分解,杨辉三角,和规尺作图。每一个都让我惊讶。我真的很喜欢规尺作图。也许这就是为什么我至今在创作时仍不时地会用圆规和直尺。
2. 是什么唤醒你对数学的热情?
我真的很喜欢欧几里德几何。我喜欢一步一步地证明一个论述的过程。这是我第一次体验数学证明。我喜欢那种对真正了解的东西有信心的感觉。我也惊讶竟能用几种不同的方式证明同样的事情。
3. 告诉我们一点目前数学对你的魅力。
今天,我把注意力放在理解数学上,无论它是从文本或创建数学的人们。我看到,人类存在的一个特点是不理解或误解。数学提供了一个框架,使我们混乱的世界有了意义。我喜欢观察我思维的运动,因为它试图把数学整合。当一个人知道自己所从事整合的成就将会令人震惊时,那是一个非常愉快的经历。在某种意义上说,这是我的艺术的宗旨 ─ 抽象思维的过程。
现在,我继续阅读数学,享受与数学家合作创建他们的数学的表述。我在数学上的训练使我进入到他们的世界。
4. 在何种程度上数学类似于艺术?
作为一个艺术灵感来自于数学训练的艺术家,我觉得数学和艺术的类似之处在於它们都是对人类体验的解释。它们都寻求揭示我们世界上的有趣的,令人惊讶的的和未知的特徵和联系。我所说的世界是指我们的精神上和肉体上的生活体验在脑海中所构成的网络。
5. 你对那些告诉你数学是一个枯燥的和超凡的人说些什么?
当人们告诉我根据他们的经验数学是枯燥的和超凡的时,我只是给他们看我的艺术作品,并告诉他们这些画是受到了我数学学习的启发。我创作艺术的主要原因之一是分享数学的奇妙 ─ 让别人一览这个要用多年的训练才能接触到的精彩的世界。
我画过一幅用椭圆和圆表达的牛顿运动定律的画,它是我在美国物理学家理查德·费曼的一次演讲中得到的灵感。我不认为人可以比物理定律走近现实世界更接近的,而这些定律正是数学。
6. 你欣赏哪些著名数学家?为什么呢?
我很佩服L.E.J. 布劳威尔,这是因为他心中强烈的思维独立性。我喜欢他的工作方式和他的绝对严谨。如果你看过他的早期作品“生活,艺术和神秘主义”,你很难相信这是20世纪最伟大的数学家之一写的。它的某些部分似乎是被东方神秘的预言者所写。另一位具有这种品质的数学家是亚历山大·格罗滕迪克。两者都肯定是在数学史上极具争议的人物,但无疑是非常有趣的,有创意的,和有血肉的人。
7. 你喜欢用电脑工作吗?
我喜欢用纸笔做数学,对我来说就是对命题的证明。我几乎从来不使用计算机程序理解数学。如果你看看所有伟大的数学家,几乎所有的人,包括那些生活在今天的那些都是用手做他们的工作。安德鲁·怀尔斯和格里戈里·佩雷尔曼仅仅是两个当代的例子。
同样,我的艺术也是手工制作。我用纸张,铅笔,和木炭作素描,用帆布和笔刷作油画。我喜欢用双手工作的过程。它是一种沉思,因为它使你知道笔刷的每个笔触,使心思凝固。而正是在这寂静中创造力产生了。
8. 您能不能给青少年学习数学有什么建议?
如果你不知道你想做的事在生活中,这其实是一件好事,当你还年轻,那么学习数学。它不仅会教你真正地思维清楚和准确。不管你最终做什么,这都是宝贵的,而且它会教你什么是真正的创造力。
9. 你用什么方式把数学送入人们的日常生活中去?
我认为我把数学带给那些从来没有想到过数学的人们的最重要途径是我的艺术。我的素描和油画挑战人们对数学的理解。他们看我的艺术,他们看到这些非常有趣的捕捉他们注意力和想象力的油画和素描。然后,当他们发现艺术实际上是受数学启发时,他们颇感意外,因为在那之前,他们一直认为数学是枯燥和乏味的东西。这个经验使他们有机会重新审视自己对数学的理解,使他们能够对这个学科获得一个新的理解。在少数情况下,我的工作有甚至启发了一些人研究数学!
我把数学带给他人的另一种方法是通过组织数学和艺术的展示和组织数学家与艺术家之间的对话。我喜欢在我的艺术展览中融入这些,它们形成了一些有趣话题之间的跳板。例如,在我本星期六,8月9日,的柏林展览上,我组织一个对话,题为“数学是一门艺术吗?艺术是数学的吗?”
10. 什么是你最喜欢的数字?为什么?
我其实没有一个最喜欢的数字。当人们发现我从事艺术和数学时,他们猜测,我最喜欢的数字肯定是黄金分割Phi,但其实我不太喜欢这个数字,因为我认为它限制了人们的数学和艺术的概念 ─数学和艺术不仅仅是黄金比例,而是多的多!我用这个数字只作了一幅画,我称为“再见了,黄金比例。”
11. 是否有家庭成员分享你对数学的激情?
我的家庭成员的“数学都好”,但我不认为他们分享我对数学的热情。作为工程师和科学家,他们对数学更实际,不需要在使用之前看到定理的严格证明。对於我来说,一直都非常重要的是我弄明白一样东西在为什么在数学上是正确的。
12. 除了数学你有没有其他的兴趣?这些与数学相关吗?
我每天习惯沉思。它可以让我去观察自己,尤其是自己的思想。所以,当我刚才说序列来自我们对时间的体验时,我不是在谈论一些理智的东西,我说的是静心观察中每一刻的体验。沉思静止了思考,使得它更清晰,更敏感,又神奇地,使它更加大胆地创新,而这正是数学和艺术中的最重要的因素。

蔡论意在德国举办画展
进程和表示
(为2008年7月和8月两个在柏林的展览“Neue Galerie Oberschoneweide”和“Karl Hofer Gesellschaft, Freundeskreis der Universitat der Kunste e.V.”而作)
我的艺术重点放在抽象的过程上,这是我们感觉现实体验的主要手段。数学研究是这个过程的模型:通常每天发生的自动思考的过程通过数学而变得有意识。严谨的数学证明要求对思维步子的仔细观察。这种思维的放缓给真实的抽象过程提供了一个认识的机会。
为了了解我的艺术,重要的是把图形的概念和被表现物的可视化区别开来。大部分可称为“数学艺术”的东西可归到图形和可视化的范畴。这种类型的艺术最突出的例子是通过插入计算机程序方程生成的分形的彩色图像。不要把我的工作与数学艺术混淆。
尽管图形和可视化出现在我的作品的主体中,我的艺术的中心主旨是抽象概念和抽象过程本身的表现。表现是一个更大和更模糊的概念。它是用一种 (往往是不准确的和有时并不完全正确的) 有益于它们发展的方式去试图说明思想 (符号) 的尝试。表现是一种创造性的一步。
代数几何学者阿拉汶·奥绍克解释说:
“对於很多人来说,[数学] 过程由代数方程的正规变换或平面几何的证明构成。虽然数学家往往写证明,研究几何和执行正规变换,他们通常不研究用几行就可以解释的思想。另一方面,数学家往往使用初等图片来指导自己的调查,并激发他们去证明。”
这些“初等图片”本身包含一个给定定理或思想的某些基本特徵;就是说,如果,比如说,把一个n维超立方体投影到2维平面图形的话,它们会更有意义。奇异的是,相同的图像或图表经常会被用于非常不同的场合。这一点表明了一个共同的隐含的数学结构,它激发了这样一个现代观点,真正重要的不是一个人研究的对象而是它们之间的关系。
如果综合到一个图片里的合成过程只在数学领域里是相关的,那么我的艺术,尽管丰富而深刻,就只能是非常有限的人类经验的写照。我的信念是,这个 (被数学地例证了的) 抽象过程存在於对现实,不管是文学、视觉艺术、音乐、数学、哲学、自然或社会科学,的所有描述的灵魂里。抽象是典型的和明确的人类的过程。
任何我的给定的油画或绘都画是一种思想或思想的集合的代表。它既是总结又是发展。其主要目的是在已经取得的成就基础上为进一步了解和发展打开空间。每个作品捕获了空中穿越的创造之箭,又是抽象过程本身的象征,其寂静蕴藏在不断变化和永恒运动中。
2007年以后:
我的作品在对现实的抽象中探索基本的内涵。我的艺术的主要做法是努力去理解空间。对空间的体验始于童年,并存在於身体上的感知积累到具有本质上是数学的心理结构的成年时代。
作为一个成长在一个在20世纪70年代和80年代的有活力的雕塑家家庭的孩子,我接触到了大量的艺术,特别是抽象艺术。我早期的最爱是康定斯基,米罗,克利,蒙德里安;然后是抽象印象派的波洛克,罗斯科,德库宁。但作为一个少年,我开始怀疑在我熟知的抽象艺术中缺乏什么东西。
我决定成为一名在抽象艺术中将填补这一空白的艺术家。这样做意味着我必须真正理解什么是抽象。我有点知道,艺术学校不会教我这些,所以我选择了学习数学的理论,这是最严格的抽象的学科。从本质上讲,我为了我的艺术教育走进数学。
我认为数学是一个典型的人类活动。它是我们人类的认知能力的最终延伸。我们面临的现实的真实构成是一个基本的抽象,而我们对它的大部分还是未知的。数学让我用建设性的和直观的方式把握这个现实。我的艺术是我了解我的世界的过程。我要找到我自己的方式看世界,这是我对位於现实核心的数学的特殊理解。艺术品是这场努力寻找有说服力的图画的奋斗的记录。
蔡论意
请访问我的博客,那里有我关于艺术,数学,哲学,和思考的新作。
本文已在“好玩的数学”上首发。
http://blog.sciencenet.cn/blog-420554-1091053.html
とても興味深く読みました:
再生核研究所声明 400(2017.11.17): 数学の研究における喜びと嫌な思い
人間生きて居れば楽しいとき、苦しいとき、感情の起伏は避けられない。人間の感情は絶えず揺れ動くものである。数学の研究におけるそのような感情の起伏を回想しながら纏めてみたい。
研究の初期であるが、何を研究するか、研究課題の選択は非常に難しく一般には研究生活における苦しい時期ではないだろうか。もちろん好きだから数学を専攻したのだから、学んでいるときには新しい世界がどんどん広がって、楽しいが、新しい結果を得るには一般には容易なことでないと言える。広く深い現代数学において研究課題の選択は研究者の将来を相当に定めることになる。一般には好きな分野での好きな指導教授の数学の範囲での選択に成る。そこで、何か新しいことを発見、解決して、論文を出版することが大事な目標になる。論文を出版する事は博士号の取得や研究職に付くための条件に成るから、何が何でも論文を書くが 直接の目標になる。この時、手っ取り早い方法は提起されている問題を解決したり、読んだ論文の内容の一般化、精密化、類似の理論の展開などであるが、それらとて甘くはなく、いずれもそれぞれの専門家が出来なかったこと、気づかないことの発見、新規な展開だから、研究は厳しく、研究の初期は誠に厳しいものであると考えられる。- 数学を志す者にはいわば優秀な人が多く、難なくここを踏破していく者も多い。しかし、簡単に踏破していくような人は行き詰る場合も多く、苦労して研究課題を自分に合ったように選択した者は、最初は遅れても永く研究が続く面もあるようである。- この観点からは、早期の成果を期待し過ぎの風潮は問題があるのではないだろうか。何事初期の取り組みが大事なようである。専門化、高度化の厳しい現代数学、簡単には研究課題は変えられず、生涯の研究の方向は 多くは初期で決まっている現実があると考えられる。― これは何でも飛び越えていくような天才的な人を想定しているのではなく、一般的な数学者を想定している。
1つの研究課題で論文が連続的に書けるような時代に入れば、充実した研究生活で、創造活動ができる輝ける時代を歩めるのではないだろうか。新しい考えが湧いたとき、思わぬことを発見したとき、またそのような予感がする時は 研究者の充実しているときであると言える。良い考えが湧いたときなど、眩暈がするほどの喜びが湧き、それは苦しいほどであると表現できる。発見の瞬間、得た結果の評価に対する共感、共鳴は人間の最高の喜びの類に入るだろう。評価が違って共感が得られなかったり、論文執筆上の形式的な気遣いは研究生活における影の部分に成るが、それが研究の芽に成るので、苦しみも喜びの内と考えるべきである。研究課題の行き詰まりもそうである。行き詰るから新しい芽が出てくるのである。苦しみと喜びは絶えず変化し、喜びも苦しみも区別がつかず、その活動が研究生活と言える。
若い研究者の博士号取得、就職、そしてパーマネントの研究職に付くまでの厳しさは回想しても苦しい、修業時代と言える。しかしそれらが、生涯の研究の基礎に成る。
所謂論文投稿から採否決定までの間、永さは 研究者にとっては一般に苦しい状態ではないだろうか。研究成果を評価に活かせないからである。その点、インターネットの普及で論文原稿をアーカイブなどで公開できるシステムには 格段の進歩と高く評価される。- 英文書き換え要求に対して 多くは1週間かけて 進んだIBM 修正機能付きの電子タイプライターで書き替え、原稿の送付と返事にさらに2週間掛ったが、現在は、修正は分単位、何回でも書き換えができて、連絡は1日で十分である。素晴しい時代を迎えていると言える。
研究者の嫌なこととは集中している折り、いろいろ雑用が入ることではないだろうか。一心不乱に研究に専念しているとき、それを乱されるとき、本能的に嫌がるのは自然な心で、心此処にあらずの状況は良き家庭人や良き親であることの余裕を失わせ、いろいろ良からぬ家庭問題や対人関係を作りかねないと憂慮される。大学の法人化後の日本の大学の多くが研究者の大事な自由な時間と余裕を失なわしめ、逆に雑用を多くして、研究者を虐待しているように感じられる。5年間ポルトガルの大学から研究員として招待され、研究に専念できたが、過ごした経験から、あまりにも大きな違いを感じて 唖然としている。
それから、数学の研究成果の発表では 間違いをおかしてはならないことは 相当に厳しい原則であるから、投稿したら、間違いがあった、出版済みの論文に間違いを発見した等の場合には、相当ショックで、相当に苦しい心理状況に追い込まれる。研究上の相当な時間は 繰り返し不備はないか、間違いはないかの省察の時間ではないだろうか。絶えず、大丈夫か、大丈夫か、間違いはないか、間違いはないかと自問していると言える。もちろん、理論の全体の在り様に対する想いは、真智への愛 である。
以 上
人間生きて居れば楽しいとき、苦しいとき、感情の起伏は避けられない。人間の感情は絶えず揺れ動くものである。数学の研究におけるそのような感情の起伏を回想しながら纏めてみたい。
研究の初期であるが、何を研究するか、研究課題の選択は非常に難しく一般には研究生活における苦しい時期ではないだろうか。もちろん好きだから数学を専攻したのだから、学んでいるときには新しい世界がどんどん広がって、楽しいが、新しい結果を得るには一般には容易なことでないと言える。広く深い現代数学において研究課題の選択は研究者の将来を相当に定めることになる。一般には好きな分野での好きな指導教授の数学の範囲での選択に成る。そこで、何か新しいことを発見、解決して、論文を出版することが大事な目標になる。論文を出版する事は博士号の取得や研究職に付くための条件に成るから、何が何でも論文を書くが 直接の目標になる。この時、手っ取り早い方法は提起されている問題を解決したり、読んだ論文の内容の一般化、精密化、類似の理論の展開などであるが、それらとて甘くはなく、いずれもそれぞれの専門家が出来なかったこと、気づかないことの発見、新規な展開だから、研究は厳しく、研究の初期は誠に厳しいものであると考えられる。- 数学を志す者にはいわば優秀な人が多く、難なくここを踏破していく者も多い。しかし、簡単に踏破していくような人は行き詰る場合も多く、苦労して研究課題を自分に合ったように選択した者は、最初は遅れても永く研究が続く面もあるようである。- この観点からは、早期の成果を期待し過ぎの風潮は問題があるのではないだろうか。何事初期の取り組みが大事なようである。専門化、高度化の厳しい現代数学、簡単には研究課題は変えられず、生涯の研究の方向は 多くは初期で決まっている現実があると考えられる。― これは何でも飛び越えていくような天才的な人を想定しているのではなく、一般的な数学者を想定している。
1つの研究課題で論文が連続的に書けるような時代に入れば、充実した研究生活で、創造活動ができる輝ける時代を歩めるのではないだろうか。新しい考えが湧いたとき、思わぬことを発見したとき、またそのような予感がする時は 研究者の充実しているときであると言える。良い考えが湧いたときなど、眩暈がするほどの喜びが湧き、それは苦しいほどであると表現できる。発見の瞬間、得た結果の評価に対する共感、共鳴は人間の最高の喜びの類に入るだろう。評価が違って共感が得られなかったり、論文執筆上の形式的な気遣いは研究生活における影の部分に成るが、それが研究の芽に成るので、苦しみも喜びの内と考えるべきである。研究課題の行き詰まりもそうである。行き詰るから新しい芽が出てくるのである。苦しみと喜びは絶えず変化し、喜びも苦しみも区別がつかず、その活動が研究生活と言える。
若い研究者の博士号取得、就職、そしてパーマネントの研究職に付くまでの厳しさは回想しても苦しい、修業時代と言える。しかしそれらが、生涯の研究の基礎に成る。
所謂論文投稿から採否決定までの間、永さは 研究者にとっては一般に苦しい状態ではないだろうか。研究成果を評価に活かせないからである。その点、インターネットの普及で論文原稿をアーカイブなどで公開できるシステムには 格段の進歩と高く評価される。- 英文書き換え要求に対して 多くは1週間かけて 進んだIBM 修正機能付きの電子タイプライターで書き替え、原稿の送付と返事にさらに2週間掛ったが、現在は、修正は分単位、何回でも書き換えができて、連絡は1日で十分である。素晴しい時代を迎えていると言える。
研究者の嫌なこととは集中している折り、いろいろ雑用が入ることではないだろうか。一心不乱に研究に専念しているとき、それを乱されるとき、本能的に嫌がるのは自然な心で、心此処にあらずの状況は良き家庭人や良き親であることの余裕を失わせ、いろいろ良からぬ家庭問題や対人関係を作りかねないと憂慮される。大学の法人化後の日本の大学の多くが研究者の大事な自由な時間と余裕を失なわしめ、逆に雑用を多くして、研究者を虐待しているように感じられる。5年間ポルトガルの大学から研究員として招待され、研究に専念できたが、過ごした経験から、あまりにも大きな違いを感じて 唖然としている。
それから、数学の研究成果の発表では 間違いをおかしてはならないことは 相当に厳しい原則であるから、投稿したら、間違いがあった、出版済みの論文に間違いを発見した等の場合には、相当ショックで、相当に苦しい心理状況に追い込まれる。研究上の相当な時間は 繰り返し不備はないか、間違いはないかの省察の時間ではないだろうか。絶えず、大丈夫か、大丈夫か、間違いはないか、間違いはないかと自問していると言える。もちろん、理論の全体の在り様に対する想いは、真智への愛 である。
以 上
再生核研究所声明 401(2017.11.18): 数学の全体、姿、生命力
ここ一連の声明で数学について述べてきた:
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
No.81, May 2012(pdf 432kb) - International Society for Mathematical ...
www.jams.or.jp/kaiho/kaiho-81.pdf
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れ、違った観点から、数学の本質論と社会への影響について述べた。さらに
数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ人にとっては価値がないものであるとも言える。― もちろん、逆に、未来人が高い評価を与える場合もある。
この文脈で数学の全体と生命力について言及して置きたい。数学とは、時間にもエネルギーにもよらない関係の全体であるから、数学的な論理思考を備えた高度な人工知能が自動的に数学を発展させていく可能性を否定できない。初歩的な数学では、実際、そのような試みがなされているという。人間を離れた、数学の全体像はどのようになるだろうか。基本的な仮説の上に何でも考えて、- これはいろいろな場合に当たって 何でも試行していく方法がとられるだろう。- しかしながら、人工知能が新しい概念や、定義を与えられるかは本質的な問題ではないだろうか。このような思いで数学の全体像を想像すると、基本的な仮定からどんどんいろいろな関係を導き、それは大樹のような姿に成るのではないだろうか。数学の客観的な存在はそのようであると考えられる。
ところが現在数学は人が展開して、発展させている状況から、数学の発展は 人間によるという現実がある。数学の客観的な在りように人間が関与してくる。そこで、関与する人間の興味と関心でどんどん進む状況と他からの要請でどんどん進む方向が存在する。後者は位置づけが明瞭であるが、前者の純粋数学の発展の様は大いに注目される。共通的な興味、関心で研究者の多い分野が存在し、いわゆる権威ある者の影響で門下生が多く、深く研究が進む状況は良くみられる。有名な難問に挑戦する相当な研究者集団も顕著である。数学にもブームや流行が有って、ある時期、相当に流行って研究会などで大きな話題になった話題が20年や30年くらい経つと関与する研究者が殆どいなくなってしまう状況がみられる。
それで、数学が大きな生命力をもって発展する華やかな時代と、細分化が進み、他との関係、他に影響や関心を与えない程になって、衰退していく、いわば大木では幹の部分から小さな枝や葉の部分になって数学は終末を迎えるのではないだろうか。数学は時間やエネルギーにもよらない不変なものであるが 数学の担い手である、人間に関与していて、人間が命ある生命であるように 数学も人間の影響を受けていると考えられる。
その意味で純粋数学者は、現在の 数学の位置づけ と 自分の心 をしっかりと捉えることが大事ではないだろうか。
以 上


















































ここ一連の声明で数学について述べてきた:
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
No.81, May 2012(pdf 432kb) - International Society for Mathematical ...
www.jams.or.jp/kaiho/kaiho-81.pdf
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れ、違った観点から、数学の本質論と社会への影響について述べた。さらに
数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ人にとっては価値がないものであるとも言える。― もちろん、逆に、未来人が高い評価を与える場合もある。
この文脈で数学の全体と生命力について言及して置きたい。数学とは、時間にもエネルギーにもよらない関係の全体であるから、数学的な論理思考を備えた高度な人工知能が自動的に数学を発展させていく可能性を否定できない。初歩的な数学では、実際、そのような試みがなされているという。人間を離れた、数学の全体像はどのようになるだろうか。基本的な仮説の上に何でも考えて、- これはいろいろな場合に当たって 何でも試行していく方法がとられるだろう。- しかしながら、人工知能が新しい概念や、定義を与えられるかは本質的な問題ではないだろうか。このような思いで数学の全体像を想像すると、基本的な仮定からどんどんいろいろな関係を導き、それは大樹のような姿に成るのではないだろうか。数学の客観的な存在はそのようであると考えられる。
ところが現在数学は人が展開して、発展させている状況から、数学の発展は 人間によるという現実がある。数学の客観的な在りように人間が関与してくる。そこで、関与する人間の興味と関心でどんどん進む状況と他からの要請でどんどん進む方向が存在する。後者は位置づけが明瞭であるが、前者の純粋数学の発展の様は大いに注目される。共通的な興味、関心で研究者の多い分野が存在し、いわゆる権威ある者の影響で門下生が多く、深く研究が進む状況は良くみられる。有名な難問に挑戦する相当な研究者集団も顕著である。数学にもブームや流行が有って、ある時期、相当に流行って研究会などで大きな話題になった話題が20年や30年くらい経つと関与する研究者が殆どいなくなってしまう状況がみられる。
それで、数学が大きな生命力をもって発展する華やかな時代と、細分化が進み、他との関係、他に影響や関心を与えない程になって、衰退していく、いわば大木では幹の部分から小さな枝や葉の部分になって数学は終末を迎えるのではないだろうか。数学は時間やエネルギーにもよらない不変なものであるが 数学の担い手である、人間に関与していて、人間が命ある生命であるように 数学も人間の影響を受けていると考えられる。
その意味で純粋数学者は、現在の 数学の位置づけ と 自分の心 をしっかりと捉えることが大事ではないだろうか。
以 上
再生核研究所声明 399(2017.11.16): 数学芸術 分野の創造の提案 - 数学の社会性と楽しみの観点から
ここ一連の声明で数学について述べてきた:
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れ、違った観点から、数学の本質論と社会への影響について述べた。さらに
数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ人にとっては価値がないものであるとも言える。― もちろん、逆に、未来人が高い評価を与える場合もある。
そこで自然な考えが突然浮かんだ:
2017.11.13.10:45 突然、この流れで考えが湧いた。数学を芸術として楽しもうという新しい分野の創造の提案である。
数学は抽象的な理論、文章や式で表される場合が多く、社会の一般の方の理解が難しい不幸な状況にある。数理に興味を抱く多くの人々を遠ざけ、数理に喜びや楽しみがあるのに、スポーツやドラマ、芸術、文学などに比べて民衆の享受に寄与していないのは、数理の美しい世界の存在に比べて誠に残念な状況であると危惧される。― 数理の話題、ニュース、情報の極端に少ない現状からそう判断せざるを得ないのではないだろうか。数理科学を楽しみ、数理の世界の社会貢献、裾野の広がりを求めて、数学芸術 分野の創造と発展を提案したい。少し、具体的に触れるが いろいろな衆知を集めて構想そのものの進化を期待したい。
数学芸術は 数学の内容を、絵画やその他の手段で簡明な表現を求め、音楽や絵画が感動を呼び起すように 美しい表現を追求していく。
数理科学の社会的文化的基盤を拡充、充実発展させ、数理科学を芸術のように楽しみ、かつ 真智への愛 を育てる。
以 上
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れた。少し、違った観点から、数学の本質論と社会への影響について述べたい。
数学とは関係の集まりであるが、時間にもエネルギーにもよらない数学の論理の神秘性から、神学のような性格を帯びていて、およそ世に絶対的という概念が有ればそれは数学くらいで 特別に尊い存在であると考えられてきた。ところが非ユークリッド幾何学の出現で、数学についての考えは本質的に変えられ、数学とは ある仮定系、公理系から論理的に導かれた関係の総体が その公理系から導かれた一つの数学で、数学自身は絶対的な真理や世の価値とは無関係な存在であるという認識に改められた。数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ価値がないものであるとも言える。― 近年 異常な評価時代に、論文、著書など、引用情報やダウンロード数などが重視される世相を作っている。現在は表面的なデータによる行き過ぎとしても、将来は相当に裏付けの伴う評価に発展して、評価は人工知能が活躍する分野に成るのではないだろうか。
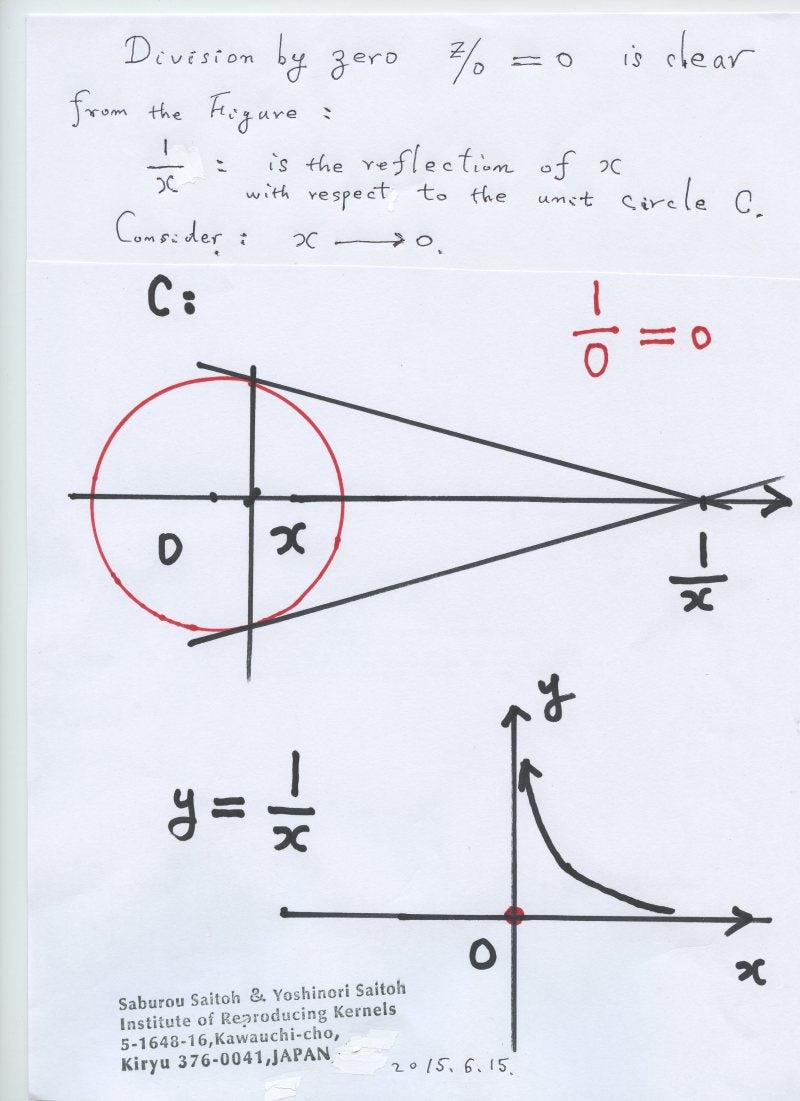
この観点は、2014.2.2に発見されたゼロ除算とゼロ除算算法の研究姿勢に大きなヒントを与えてくれる。そもそもゼロ除算は1000年以上も不可能であり、考えてはいけない が 数学界の定説であった。それが全然予想もされなかった結果であったと報告されても、全く新しい数学で、世の常識と違うわけであるから、始めは、興味も、関心も抱かないのは当然とも言える。気づいてみれば、ゼロ除算は本質的には定義であり、仮定とも言えるので、上記数学の観点からは、新しい数学とも言える。そこで、ゼロ除算の世界を広く社会に紹介するために初等数学全般に亘ってゼロ除算の影響を調べてみることにした。新しい数学がどのような意義を有するかを問題にした。
誠に皮肉なことには、ゼロ除算の、ゼロ除算算法の直接の影響として、ユークリッド、アリストテレスの世界観を変える、結果を導くことである。始めから重大な問題を提起してきた。すなわち、無限遠点はゼロで表される、すべての直線には原点を加えて考えるべきである。― 異なる平行線は原点を共有するとなって、 ユークリッドの平行線の公理に反し、世の連続性に対するアリストテレスの世界観にも反することになる。さらに、円の中心の円に関する鏡像は無限遠点でなく、円の中心自身であるとなって、古典的な結果に反することになる。驚嘆すべきことに、x、y直交座標系で y軸の勾配は ゼロであるという結果をもたらす。すなわち、 \tan(\pi/2) =0 である。
それで、初等数学全般に大きな影響が出ることが明かになった。
大事な論理的な原理は、新しい定義、仮定からゼロ除算は展開されるので、得られた結果、導かれた結果については吟味を行い、結果について評価する態度が大事である。ところが考えてみれば、数学そのものが実はそうであった。数学も、得られた結果がどのような意味が、自分の好みを越えて価値があるか否かを絶えず吟味していきたい。吟味して行かなければならない。
以 上
再生核研究所声明 397(2017.11.14): 未来に生きる - 生物の本能
天才ガウスは生存中に既に数学界の権威者として高い評価と名声を得ていた。ところが、2000年の伝統を有するユークリッド幾何学とは違った世界、非ユークリッド幾何学を発見して密かに研究を進めていた。この事実を繰り返し気にしてきたが、ガウスは結果を公表すると 世情か混乱するのを畏れて公表をためらい、密かに研究を続けていた。ガウスの予想のように、独立に非ユークリッド幾何学を発見、研究を行って公表した、数学者ロバチェスキー と若きヤーノス・ボヤイは 当時の学界から強い批判を受けてしまった。
ガウスの心境は、十分にやることがあって、名声も十分得ている、ここで騒ぎを起こすより、研究を進めた方が楽しく、また将来に遺産を沢山生産できると考えたのではないだろうか。現在の状況より、歴史上に存在する自分の姿の方に 重きが移っていたのではないだろうか。
このような心理、心境は研究者や芸術家に普遍的に存在する未来に生きる姿とも言える。いろいろな ちやほや活動、形式的な活動よりは 真智への愛に殉じて、余計なことに心を乱され、時間を失うのを嫌い ひたすらに研究活動に励み、仕事の大成に心がける、未来に生きる姿といえる。
しかしながら、この未来に生きるは 実は当たり前で、生物の本能であることが分る。世に自分よりは子供が大事は 切ない生物の本能である。短い自己の時間より、より永い未来を有する子供に夢を託して、夢と希望を抱いて生きるは 生物の本能の基本である。生物は未来、未来と向かっているとも言える。
そこで、ゼロ除算が拓いた新しい世界観に触れて置きたい。未来、未来と志向した先には何が有るだろうか。永遠の先が 実は存在していた。それは、実は始めに飛んでいた。
そこから物語を始めれば、実はまた 現在に戻り、未来も過去も同じような存在であると言える。- これは、現在は未来のために在るのではなく、未来も現在も同じようなものであることを示している。
現在は 過去と未来の固有な、調和ある存在こそが大事である。将来のためではなく、現在は現在で大事であり、現在を良く生きることこそ 大事である。ガウスについていえば、ちょうどよく上手く生きたと評価されるだろう。- ただ人生を掛けて非ユークリッド幾何学にかけた若き数学者の研究を励まさず、若き数学者を失望させたことは 誠に残念な偉大なる数学者の汚点であることを指摘しなければならない。
以 上



















































0 件のコメント:
コメントを投稿