2017年12月27日水曜日

文字を持たなかったインカ帝国で記録用に使われた結び目つきのひも「キープ」の解読に大学生が成功

13世紀から16世紀にかけて南アメリカに存在したインカ帝国は、文字を持たない文明だったため、その歴史についてわかっていることは限られています。しかし、結び目を使って出来事などを記録する「khipus(キープ)」と呼ばれるひもをインカ文明で使っていたことがわかっており、この「意味」の解読作業が続けられています。そんな中、ハーバード大学の学生が春休みを利用してキープの解読作業に着手し、それまでわかっていなかった秘密を探り当てることに成功しています。

The College Student Who Decoded the Data Hidden in Inca Knots - Atlas Obscura
https://www.atlasobscura.com/articles/khipus-inca-empire-harvard-university-colonialism

インカ帝国では文字を使っていなかったため、文明に関する記録はほとんど残っていません。マチュ・ピチュのような壮大な建造物が現代にも残されているのとは対照的に、インカ帝国に関してわかっていることは、もっぱらインカ帝国を征服したスペイン人が残した記録ばかり。しかし、これらのインカ帝国史はあくまでも侵略者側から見た見解であり、インカ文明を正確に反映したものではないという考えの考古学者は多く、そのためインカ人が記録用に使用したひも「キープ」の解読作業が世界中で行われています。

ハーバード大学の1年生だったマニー・メドラノさんは、たまたま受講したゲイリー・ウルトン教授の考古学の授業で、インカ帝国で使われていたキープの存在を知りました。ウルトン教授自身もキープの解読作業を進めていますが、講義の中で「興味のある学生はまとまった時間のある春休みに記録の解読作業をしてみてはどうか」と学生たちに話したところ、メドラノさんは強く興味を引きつけられました。「過去の秘密を見つけたい、という思いがどこから来たかはわかりませんが、私の中に確かに芽生えました」とメドラノさんは講義中に受けた衝動について述べています。

メドラノさんの志願を受けてウルトン教授は6本のキープを提供して、インカ式簿記の解読作業が始まりました。この6本のキープについてウルトン教授は、偶然にも同じSanta Valley地域の同じ時代に記録されたスペインの国勢調査文書を見つけていました。この国勢調査記録とキープを照らし合わせることで、メドラノさんはキープに記録された内容の解読作業を行いました。

メドラノさんはウルトン教授から提供された資料をもとに、Microsoft Excelのスプレッドシートにデータを入力し、一部のデータはグラフ化してパターンを探ったとのこと。メキシコ系アメリカ人の家庭に生まれたメドラノさんは、スペイン語の読み書きができたためスペイン語で書かれた国勢調査の読解にはまったく支障がありませんでした。また、経済学を専攻していたため数字やデータを取り扱うことにも問題はなし。さらにパズルや数独を解くのが大好きなメドラノさんにとって、キープの解読作業はこれらのゲームよりもはるかに深遠な行為に感じたそうで、キープという大きな読解作業にとってメドラノさんはうってつけの資質を備えていたようです。

メドラノさんは解読作業によって、各キープの結び目の方式が国勢調査に記録された132人の社会的地位にあまりにも強すぎる相関関係があることを発見。春休みが終わってすぐにウルトン教授にコードに関する理論を明かしました。「なんてことだ! この青年は確かにやり遂げた、と私はかなり興奮したことを覚えています」とそのときの衝撃についてウルトン教授は述懐しています。

その後もメドラノさんとウルトン教授によるキープの共同解読作業が続けられました。ウルトン教授いわく「何かを指摘すると1、2週間後にはさらに深い何かを理解する」というメドラノさんのすさまじい読解能力によって、「ペンダントコードがトップのコードに結びつく様式が、個人が所属する社会的グループを示している」という事実を突き止めることに成功しました。これはもちろん世界初の発見であり、この研究成果は科学誌Ethnohistoryに査読を経た後、2018年1月に論文として掲載される予定です。この論文ではメドラノさんが第一著者を務めており、メドラノさんの貢献度の高さがうかがわれます。

この研究成果についてセントアンドリュース大学でアンデス人類学を研究するサビン・ハイランド博士は、「メドラノさんの発見は世界で初めての内容で、スリリングなものです」と高く評価しています。ウルトン教授によると、今回の発見を足がかりに、さらに多くの発見がもたらされることが期待できるとのこと。征服者による歴史から離れて、インカの歴史をその土地の観点から理解できる可能性について、メドラノさんとウルトン教授は興奮しているそうです。

https://gigazine.net/news/20171226-inca-khipus-decode/

とても興味深く読みました：考古学に興味があります：

Announcement 213: An interpretation of the identity $ 0.999999...... =1$

カテゴリ：カテゴリ未分類

\documentclass[12pt]{article}

\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}

\numberwithin{equation}{section}

\begin{document}

\title{\bf Announcement 213: An interpretation of the identity $ 0.999999...... =1$

}

\author{{\it Institute of Reproducing Kernels}\\

Kawauchi-cho, 5-1648-16,\\

Kiryu 376-0041, Japan\\

E-mail: kbdmm360@yahoo.co.jp\\

}

\date{}

\maketitle

{\bf Abstract: } In this announcement, we shall give a very simple interpretation for the identity: $ 0.999999......=1$.

\bigskip

\section{ Introduction}

On January 8, 2008, Yuusuke Maede, 8 years old boy, asked the question, at Gunma University, that (Announcement 9(2007/9/1): Education for genius boys and girls):

What does it mean by the identity:

0.999999......=1?

at the same time, he said: I am most interesting in the structure of large prime numbers. Then, a teacher answered for the question by the popular reason based on the convergence of the series: $0.9, 0.99, 0.999,... $. Its answer seems to be not suitable for the 8 years old boy with his parents (not mathematicians). Our answer seems to have a general interest, and after then, such our answer has not been heard from many mathematicians, indeed.

This is why writting this announcement.

\medskip

\bigskip

\section{An interpretation}

\medskip

In order to see the essence, we shall consider the simplist case:

\begin{equation}

\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + ... = 1.

\end{equation}

Imagine a tape of one meter length, we will give its half tape: that is,

\begin{equation}

\frac{1}{2}.

\end{equation}

Next, we will give its (the rest's half) half tape; that is, $\frac{1}{2}\cdot \frac{1}{2} = \frac{1}{2^2}$, then you have, altogether

\begin{equation}

\frac{1}{2} + \frac{1}{2^2} .

\end{equation}

Next, we will give the last one's half (the rest's half); that is, $\frac{1}{2}\cdot \frac{1}{2} \cdot \frac{1}{2}= \frac{1}{2^3}$,

then, you have, altogether

\begin{equation}

\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3}.

\end{equation}

By this procedure, you will be able to obtain the small tapes endressly. Imagine all the sum as in the left hand side of (2.1). However, we will see that this sum is just the division of the one meter tape. Therefore, we will be able to confim the identity (2.1), clearly.

The question proposed by Y. Maede is just the small change the ratio $\frac{1}{2}$ by $\frac{9}{10}$.

\bigskip

\section{ Conclusion}

Y. Maede asked the true sense of the limit in the series:

0.999999.....

that is, this series is approaching to 1; however, is it equal or not ? The above interpretation means that the infinite series equals to one and it is just the infinite division of one. By this inverse approarch, the question will make clear.

\medskip

\bigskip

\section{Remarks}

Y. Maede stated a conjecture that for any prime number $p$ $( p \geqq 7)$, for $1$ of $ - 1$

\begin{equation}

11111111111

\end{equation}

may be divided by $p$ (2011.2.6.12:00 at University of Aveiro, by skype)

\medskip

(No.81, May 2012(pdf 432kb)

www.jams.or.jp/kaiho/kaiho-81.pdf).

\medskip

This conjecture was proved by Professors L. Castro and Y. Sawano,

independently. Y. Maede gave later an interesting interpretation for his conjecture.

\medskip

(2015.2.26)

\end{document}

\title{\bf Announcement 214: Surprising mathematical feelings of a 7 years old girl

}

\author{{\it Institute of Reproducing Kernels}\\

Kawauchi-cho, 5-1648-16,\\

Kiryu 376-0041, Japan\\

E-mail: kbdmm360@yahoo.co.jp\\

}

\date{}

\maketitle

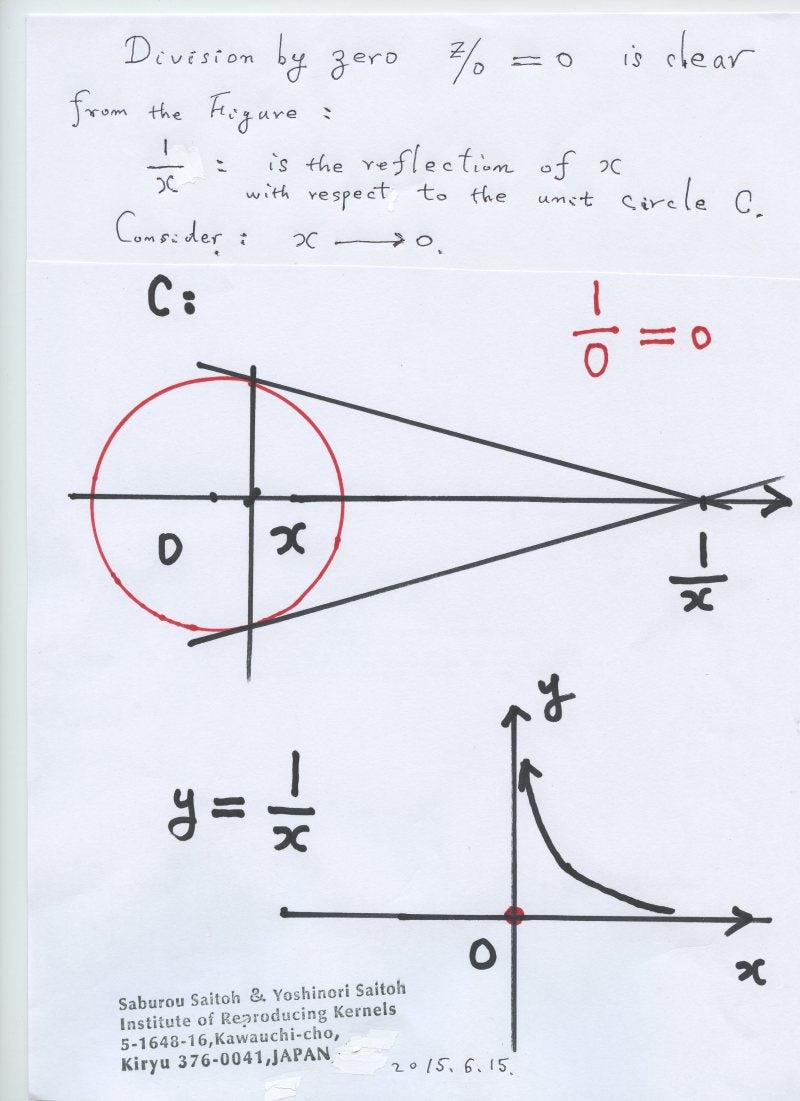
{\bf Abstract: } In this announcement, we shall give the two surprising mathematical feelings of 7 years old girl Eko Michiwaki who stated the division by 3 of any angle and the division by zero $100/0=0$ as clear and trivial ones. As well-known, these famous problems are historical, and her results will be quite original.

\bigskip

\section{ Introduction}

We had met, 7 years old girl, Eko Michiwaki on November 23, 2014 at Tokyo Institute of Technology and August 23, 2014 at Kusatu Seminor House, with our colleagues. She, surprisingly enough, stated there repeatedly the division by 3 of any angle and the division by zero $100/0=0$ as clear and trivial ones. As well-known, these famous problems are historical and her results will be quite original.

\section{The division of any angle by 3}

\medskip

Eko Michiwaki said:

divide a given angle with 4 equal angles; this is simly done. Next, we divide one divided angle

with 4 equal angles similarly and the three angles add to other 3 angles. By continuing this procedure, we will be able to obtain the division by 3 of any angle. Her idea may be stated mathematically as follows:

\frac{1}{4} + \frac{1}{4^2} + \frac{1}{4^3} + ... ...= \frac{1}{3}.

However, her idea seems to be more clear than the above mathematical formula. For this sentence, see \cite{ann3} for the sense of the limit.

\bigskip

\section{The division by zero $100/0=0$}

\medskip

As we stated in \cite{ann1}, she stated that division by zero $100/0=0$ is clear and trivial for our recent results \cite{cs,kmsy,s,ttk}. The basic important viewpoint is that division and product are different concepts and the division by zero $100/0=0$ is clear and trivial from the own sense of the division, independently of product \cite{ann1}. From the viewpoint, our colleagues stated as follows:

\medskip

On July 11, 2014, Seiichi Koshiba and Masami Yamane said at

Gunma University:

The idea for the division of Hiroshi Michiwaki and Eko Michiwaki (6 years

old daughter) is that division and product are different concepts and they

were calculated independently for long old years, by repeated addition and

subtraction, respectively. Mathematicians made the serious mistake for very

long years that the division by zero is impossible by considering that division

is the inverse operation of product. The division by zero was, however, clear

and trivial, as z/0=0, from the own nature of division.

\medskip

On February 21, 2015, Seiichi Koshiba and Masami Yamane visited our Institute and we confirmed this meaning of these sentences and the basic idea on the division by zero.

\medskip

(2015.2.27)

\bigskip

\bibliographystyle{plain}

\begin{thebibliography}{10}

\bibitem{cs}

L. P. Castro and S.Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.

\bibitem{kmsy}

M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,

New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,

Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.

\bibitem{s}

S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances inLinear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95.http://www.scirp.org/journal/ALAMT/

\bibitem{ttk}

S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics (in press).

\bibitem{ann1}

Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics,

Institute of Reproducing Kernels, 2014.10.22.

\bibitem{ann2}

Announcement 185: The importance of the division by zero $z/0=0$, Institute of Reproducing Kernels, 2014.11.28.

\bibitem{ann3}

Announcement 213: An interpretation of the identity $ 0.999999...... =1$, Institute of Reproducing Kernels, 2015.2.26.

\end{thebibliography}

\end{document}