今週の本棚:村上陽一郎・評 『フィボナッチ-アラビア数学から西洋中世数学へ』=三浦伸夫・著
毎日新聞 2016年06月12日 11時24分
(現代数学社・3024円)
今、私たちは、数学というと、ひどく難解な定理だの、公理だのを議論する、浮世離れした学問のように考えていないでしょうか。高校生が自分の将来を考える際にも、まず数学への親しみがあ…http://mainichi.jp/auth/guide.php?url=%2Farticles%2F20160612%2Fddm%2F015%2F070%2F003000c
物理学・数学は1600年代に急激に発展したというグラフ
Tuesday, October 13, 2015, 12:00 PM
10/13 晴 10時 浅草での空間線量は18ベクレル/立法メートル
「数学記号の誕生」(ジョセフ・メイザー著 松浦俊輔訳 河出書房新社 2014)
数学史の本では昨年出版された新しい本です。
体育の日はこれを読んでいました。
これは現代私たちが高校時代に悩まされた、あの忌まわしい(笑)微分積分記号や二次方程式とか、それよりもアラビア数字(0,1,2,3,4,5・・・)がどのように世界に定着していったのかを記した本です。
2500円もしますが、その価値はあるなあ。
最初は訳が固すぎて頭に入りませんが、世界史と数学史を一緒に勉強できるのでお得です(笑)
だいたいこのアラビア数字というやつはアラビア発祥ではありません。
ヒンドュー教のサンスクリット文字とペルシャ地方の文字が商業で用いるために発生したのが、現代のアラビア数字の原型です。
アラブを旅行した方はおわかりですが、中近東ではアラビア数字はほとんど目にしません。
空港で両替したお札から、バスや電車の時刻表はすべてアラビア<語>の数字です。なじみのない数字の記法なので「世界の歩き方(アラブ編)」の解説をひとときも離さずに、ひたすら解読するはめになります。
コインがいくらするのもわからないので、適当にコインを渡したらボーイが宙返りするような勢いで喜んでました。
あとで知ったのですが、最高額だったらしく(当時で500円ほど)、日当にあたるほどなんだとか。以後注意して渡すようにしました。
アラビア数字は本来ならばインド数字と呼称すべきなのですけども、インドとイスラム圏の交易で使われたためにアラビア数字と商人で使われたのが、呼称の始まりなのでいたしかたないかもしれません。
1200年頃になってアラビア数字はヨーロッパでも使われ出した
ローマ数字(Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ・・・)は計算には不便で、またゼロもないので商取引でははなはだ不便です。
そこでゼロという<位取りの記号>を用いた記述がヨーロッパの商人も使い出したのです。
この便利な数字をヨーロッパに紹介したのが、フィボナッチ(1170-1250頃)というイタリアの数学者がリベル・アバチという書籍で紹介して広く知られるようになりました。
フィボナッチというと、ウサギのつがいが毎月子供を産んでいくと一年後には何匹になるかというよく知られた算術問題で有名です。高校でもフィボナッチ数列という名前で教科書に載っていますね。
フィボナッチさんはイタリア商人の息子なので、貿易で使われる数字になじみがあったのですね。インド数学には10進数で位取りには0をつけるだけで良いために、筆記計算に適していることを認めて紹介したのです。
ギリシャやローマでは百千万という数詞が日本と同様にあり、そろばんでは良くても大きな数字を計算には手間がかかって不便だったからです。じっさいに0を使わないで、筆算すると、そのめんどくささは実感できるでしょう。
さあ、ヨーロッパに数字を使った解決方法(代数という数字だけの算術方式)が導入されると、爆発的に数学が進歩しました。
それまでは幾何学(天文学)という図形、つまり定規とコンパスだけで解くことが数学の能力であったし、それはキリスト教聖職者たちの秘技でもありました。
「異端の数 ゼロ 数学・物理学が恐れるもっとも危険な概念」(林大(はやしまさる)訳 早川書房 2003) ではゼロと無限という概念はキリスト教では考えてはいけないという考えであったので、インドで0が使われてもヨーロッパでは300年も使われずにいたのです。
1400年までは「+-×÷√」という算術記号はなかった
数学者といっても数式をだらだら書くことはなく、文章で書いてます。
だから数学者は神学者でもあり文学者でもあったのです。
数学が嫌いになる理由が数学記号と数字ばかりの字面だと思います。
なぜなら私も大嫌いでしたし、吐き気とめまいを覚えましたから。
ただ学生時代に同級生が、ナビエストークス方程式などを眺めてつぶやいた一言が「・・・美しい」でしたから、文学的な要素が多分にあることは認めますし、数学を専攻する人は式に芸術性を求める傾向が強いのだとか。
1400年以前に生まれていたら、きっと理系科目の数学や物理が好きになれたのにと思います。
機械時計の発明が物理学・天文学・航海術を飛躍させた
1675年に機械式時計がオランダの天文学者、ホイヘンスによって発案されたことが物理学を発展させたのです。
それまでの物理や数学は、幾何学(図形を用いた解決法)と代数学(数式を用いた解決法)です。
そこに時間という概念が加わって、物理運動(地球や太陽、月などの運行)がだんだんわかってきました。
それまでは時刻は月の満ち欠きと日の出日の入りで測るしかなかったからです。
ところが月の周期も日照時間も一定ではありません。農業ではこれでも良かったのでしょうが、測る物差しにはなり得なかったのです。
天文観測で不可欠な時間計測ができるようになって、運動の解析が1600年代後半から飛躍的に発展しました。
ゼロや無限に限りなく近い「極限」という概念が物理学を生み出した
ニュートンとライプニッツが微分積分という算術を発案して、これがすごい成果を生み出していきます。
ゼロであってゼロじゃない、無限であって無限でないが、とにかく果てしない先の値という<ごまかし>でゼロ/無限を忌むキリスト教会を騙して(なだめて)、あらたな微分積分という<宗教>概念を発表していきます。
ええ、微分積分はキリスト教の新宗派だったのです。無限とゼロに神が宿ると半分本気でニュートンは考えたのではないでしょうか。
1600年1700年あたりの科学知識が、我々が中学、高校で習った覚えのある数学や物理です。
そして意外と私を悩ました数学や物理は、中世以降で急激に発達した学問であることがわかります。
「数学記号の誕生」(ジョセフ・メイザー著 松浦俊輔訳 河出書房新社 2014)からグラフを掲載しておきます。
このグラフを眺めると、発展の度合いが冪状(べきじょう:急激に立ち上がるグラフ)であることがわかります。
ゼロが使われ出して、数式での計算が一般化すると(それまではすべて文章で記述されていた)、連立方程式やら、その解で小数点やマイナス、虚数という概念が生まれ、数字自体でも無理数(分数や有限な小数で表せない数、例では円周率π)の研究が進みました。
この急激な数学の発展にはワオと声を上げずにはいられませんね。
鎖国下の日本でも<なぜか>この潮流に追随するかのように数学は発展した!?
この先には先のノーベル賞を受賞した素粒子、ニュートリノの世界があるのです。 異端の数 ゼロ 数学・物理学が恐れるもっとも危険な概念 (2)
Tuesday, October 6, 2015, 03:05 PM
10/6 晴 10時 浅草での空間線量は33ベクレル/立法メートル
「異端の数 ゼロ」(林大 早川書房 2003)を読了しました。
前半はゼロが中世になって西洋キリスト教圏に受入れられるまでの過程とその後
後半は現代物理学・天文学においてもアインシュタインらがゼロという特異点に苦しんだ過程です。
西暦1500年あたりまでは、ローマおよび周辺キリスト教国ではゼロは触れてはならない数であったのです。
古代エジプトから発生した幾何学(測量や建築、暦)はギリシャに広がりましたがゼロは生まれませんでした。
バビロニア地方(ペルシャ、今の紛争が絶えない中近東)にはそろばんの空の桁を表す表記はありました。
マヤ人は日時がゼロから始まる独自の暦を持っていました。21世紀の最初の年は2000年なのか2001年なのかという大論争がありましたが、この暦であればそんな問題もなかったのです。
不幸なことに現代の暦はゼロのないエジプト人そしてローマ人がつくったものです。
ギリシャ人はその宇宙観からとことんゼロを嫌った
なぜならギリシャ教の神は「比率」だったからです。いわゆる黄金比などと呼ばれている比が奥義です。ギリシャ教の指導者はご存じピタゴラス!
急進で過激な思想家です。エジプトの幾何学から形に神の意志があると信じ、数学と図形は同じ意味とされていました。
だから定規とコンパスで計算することが奥義とされていましたし、宇宙も幾何学的な構造をもつと信じられていました。弦の振動や黄金比といったものが真理であったのです。
だからゼロという概念がないという宇宙観がギリシャ哲学であったのです。
ギリシャとペルシャで戦争が起こり、ペルシャ数学がギリシャにも伝わると、ギリシャ哲学者は頭を悩ますことになります。
たとえばゼノンの「アキレスと亀(アキレスのパラドックス)」・・・極限というゼロに近づける概念です。
やがてアルキメデスがギリシャに誕生し、王冠を壊さずに金がまがい物を知る方法や、細分割して放物線の面積を求める方法などを発見していきますが、不幸にも侵攻したローマ兵に殺されてしまいました。
こうしてローマはゼロを受入れることなく、時が流れてしまいました。
それではゼロはどちらに向ったかというと、西のヨーロッパではなく、東に流れ、インドやアラブ世界で大活躍します。
ヒンデゥー教では「無」は重要な概念です。アラブではアラビア数字となり、古代ユダヤ教においては数字に意味があるという神秘主義であり、ゼロも意味ある数と受入れられました。
時が流れて、キリスト教圏もイスラム圏と貿易をする上でゼロは欠かせなくなります。イタリア商人らが計算に便利なアラビア数字を使い出したのが1200年頃、そして実用的なので教会は反対しつつも、アラビア数字はヨーロッパで受入れられていきます。
ゼロを異端とするカトリックとルネサンスで花咲く数学・美術
ヨーロッパの哲学論争には「無」と「無限」が論争の種となりました。
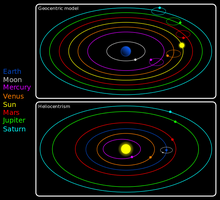
美術では遠近法(無限遠は一点に集まるという手法)、天文学ではアリストテレスの天動説からプトレマイオスの地動説へ、そしてコペルニクスの現代の太陽系モデルの提唱、そしてケプラー、ニュートンといった修道士たちがぞくぞくとカトリックの宇宙観へ反旗を翻していきます。
無と無限を否定するイエズス会にもデカルトが座標を用いることで幾何学が代数に融合できることを発見します。
ニュートン、ライプニッツが「微小」の概念を取り入れて微分積分という強力な概念を構築します。
フランス革命頃になると、果てしなく永遠と続く式も考えられるようになります。級数という概念ですね。
微分積分という新しくて強力な道具を手に入れた数学者達は、どんどん不可侵と思われていた領域へ斬込んでいきます。
18世紀にはマクローリン、テイラーというイギリスの数学者は無限に続く式も、収束するという概念を確立します。
19世紀にはガウスが虚数という概念を用いると、多次元の式でも解を求めることができることを発表します。デカルト座標が複素平面という不思議な面へと数字の世界が拡大していきます。
デカルト平面では直線でも、複素平面では円となります。さらに3次元の複素空間では球となります。
直線の運動も複素数の世界では球面の動きになる
リーマンはゼロと無限とは複素数の世界では、ちょうど地球儀の極点となることに気づきます。
こうして19世紀あたりで数学者達はゼロと無限の概念を掴みつつありました。
このゼロと無限の概念は物理学へと移り、ブラックホール理論やビッグバンという宇宙の構造をしらべる手段へと進化していくのです。
どちらも「ゼロ」という特異点、ブラックホールは重力が一点に集まったら、ビッグバンは宇宙の始まりのゼロ秒はどうであったのかを考え抜いた末の概念です。
ブラックホールの存在は確認されていますが、ビッグバンは調べようがありません。
宇宙が膨張しているという説は最近では揺れ動いています。
このように本書は非常に壮大なゼロの物語です、そして残念ながらまだ未完です。
これからもゼロに注目していきましょう。生きているうちに新たな発見がされるかもしれません。
過去ログ:異端の数 ゼロ 数学・物理学が恐れるもっとも危険な概念 (1) http://www.rokujo-radium.com/blog/?entry=entry151013-120049
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 300: New challenges on the division by zero z/0=0\\
(2016.05.22)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
%\date{\today}
\maketitle
{\bf Abstract: } In this announcement, for its importance we would like to state the
situation on the division by zero and propose basic new challenges.
\bigskip
\section{Introduction}
%\label{sect1}
By a {\bf natural extension} of the fractions
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, we found the simple and beautiful result, for any complex number $b$
\begin{equation}
\frac{b}{0}=0,
\end{equation}
incidentally in \cite{s} by the Tikhonov regularization for the Hadamard product inversions for matrices and we discussed their properties and gave several physical interpretations on the general fractions in \cite{kmsy} for the case of real numbers.
The division by zero has a long and mysterious story over the world (see, for example, Google site with the division by zero) with its physical viewpoints since the document of zero in India on AD 628, however,
Sin-Ei Takahasi (\cite{kmsy}) established a simple and decisive interpretation (1.2) by analyzing the extensions of fractions and by showing the complete characterization for the property (1.2):
\bigskip
{\bf Proposition 1. }{\it Let F be a function from ${\bf C }\times {\bf C }$ to ${\bf C }$ satisfying
$$
F (b, a)F (c, d)= F (bc, ad)
$$
for all
$$
a, b, c, d \in {\bf C }
$$
and
$$
F (b, a) = \frac {b}{a }, \quad a, b \in {\bf C }, a \ne 0.
$$
Then, we obtain, for any $b \in {\bf C } $
$$
F (b, 0) = 0.
$$
}
Note that the complete proof of this proposition is simply given by 2 or 3 lines.
\medskip
We thus should consider, for any complex number $b$, as (1.2);
that is, for the mapping
\begin{equation}
w = \frac{1}{z},
\end{equation}
the image of $z=0$ is $w=0$ ({\bf should be defined}). This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere. Therefore, the division by zero will give great impacts to complex analysis and to our ideas for the space and universe.
However, the division by zero (1.2) is now clear, indeed, for the introduction of (1.2), we have several independent approaches as in:
\medskip
1) by the generalization of the fractions by the Tikhonov regularization or by the Moore-Penrose generalized inverse,
\medskip
2) by the intuitive meaning of the fractions (division) by H. Michiwaki,
\medskip
3) by the unique extension of the fractions by S. Takahasi, as in the above,
\medskip
4) by the extension of the fundamental function $W = 1/z$ from ${\bf C} \setminus \{0\}$ into ${\bf C}$ such that $W =1/z$ is a one to one and onto mapping from $ {\bf C} \setminus \{0\} $ onto ${\bf C} \setminus \{0\}$ and the division by zero $1/0=0$ is a one to one and onto mapping extension of the function $W =1/z $ from ${\bf C}$ onto ${\bf C}$,
\medskip
and
\medskip
5) by considering the values of functions with the mean values of functions.
\medskip
Furthermore, in (\cite{msy}) we gave the results in order to show the reality of the division by zero in our world:
\medskip
\medskip
A) a field structure containing the division by zero --- the Yamada field ${\bf Y}$,
\medskip
B) by the gradient of the $y$ axis on the $(x,y)$ plane --- $\tan \frac{\pi}{2} =0$,
\medskip
C) by the reflection $W =1/\overline{z}$ of $W= z$ with respect to the unit circle with center at the origin on the complex $z$ plane --- the reflection point of zero is zero,
\medskip
and
\medskip
D) by considering rotation of a right circular cone having some very interesting
phenomenon from some practical and physical problem.
\medskip
In (\cite{mos}), many division by zero results in Euclidean spaces are given and the basic idea at the point at infinity should be changed. In (\cite{ms}), we gave beautiful geometrical interpretations of determinants from the viewpoint of the division by zero. The results show that the division by zero is our basic and elementary mathematics in our world.
\medskip
See J. A. Bergstra, Y. Hirshfeld and J. V. Tucker \cite{bht} for the relationship between fields and the division by zero, and the importance of the division by zero for computer science. It seems that the relationship of the division by zero and field structures are abstract in their paper.
Meanwhile, J. P. Barukcic and I. Barukcic (\cite{bb}) discussed recently the relation between the divisions $0/0$, $1/0$ and special relative theory of Einstein. However, their logic seems to be curious and their results contradict with ours.
Furthermore, T. S. Reis and J.A.D.W. Anderson (\cite{ra,ra2}) extend the system of the real numbers by introducing an ideal number for the division by zero $0/0$.
Meanwhile, we should refer to up-to-date information:
{\it Riemann Hypothesis Addendum - Breakthrough
Kurt Arbenz
https://www.researchgate.net/publication/272022137 Riemann Hypothesis Addendum - Breakthrough.}
\medskip
Here, we recall Albert Einstein's words on mathematics:
Blackholes are where God divided by zero.
I don't believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} [1]:
1. Gamow, G., My World Line (Viking, New York). p 44, 1970.
For our ideas on the division by zero, see the survey style announcements 179,185,237,246,247,250 and 252 of the Institute of Reproducing Kernels (\cite{ann179,ann185,ann237,ann246,ann247,ann250,ann252,ann293}).
\section{On mathematics}
Apparently, the division by zero is a great missing in our mathematics and the result (1.2) is definitely determined as our basic mathematics, as we see from Proposition 1. Note its very general assumptions and many fundamental evidences in our world in (\cite{kmsy,msy,mos}). The results will give great impacts on Euclidean spaces, analytic geometry, calculus, differential equations, complex analysis and physical problems. See our announcements for the details.
The mysterious history of the division by zero over one thousand years is a great shame of mathematicians and human race on the world history, like the Ptolemaic system (geocentric theory). The division by zero will become a typical symbol of foolish human race with long and unceasing struggles. Future people will realize this fact as a definite common sense.
We should check and fill our mathematics, globally and beautifully, from the viewpoint of the division by zero. Our mathematics will be more perfect and beautiful, and will give great impacts to our basic ideas on the universe.
\section{Albert Einstein's biggest blunder}
The division by zero is directly related to the Einstein's theory and various
physical problems
containing the division by zero. Now we should check the theory and the problems by the concept of the RIGHT and DEFINITE division by zero. Now is the best time since 100 years from Albert Einstein. It seems that the background knowledge is timely fruitful.
\section{Computer systems}
The above Professors listed are wishing the contributions in order to avoid the zero division trouble in computers. Now, we should arrange new computer systems in order not to meet the division by zero trouble in computer systems.
\section{General ideas on the universe}
The division by zero may be related to religion, philosophy and the ideas on the universe, and it will creat a new world. Look the new world.
\bigskip
We are standing on a new generation and in front of the new world, as in the discovery of the Americas.
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{bb}
J. P. Barukcic and I. Barukcic, Anti Aristotle—The Division of Zero by Zero. Journal of Applied Mathematics and Physics, {\bf 4}(2016), 749-761.
doi: 10.4236/jamp.2016.44085.
\bibitem{bht}
J. A. Bergstra, Y. Hirshfeld and J. V. Tucker,
Meadows and the equational specification of division (arXiv:0901.0823v1[math.RA] 7 Jan 2009).
\bibitem{cs}
L. P. Castro and S. Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ms}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$,
Linear Algebra \& Matrix Theory (ALAMT)(to appear).
\bibitem{msy}
H. Michiwaki, S. Saitoh, and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{mos}
H. Michiwaki, H. Okumura, and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces.
International Journal of Mathematics and Computation
(in press).
\bibitem{ra}
T. S. Reis and J.A.D.W. Anderson,
Transdifferential and Transintegral Calculus,
Proceedings of the World Congress on Engineering and Computer Science 2014 Vol I
WCECS 2014, 22-24 October, 2014, San Francisco, USA
\bibitem{ra2}
T. S. Reis and J.A.D.W. Anderson,
Transreal Calculus,
IAENG International J. of Applied Math., {\bf 45}(2015): IJAM 45 1 06.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\bibitem{ann179}
Announcement 179 (2014.8.30): Division by zero is clear as z/0=0 and it is fundamental in mathematics.
\bibitem{ann185}
Announcement 185 (2014.10.22): The importance of the division by zero $z/0=0$.
\bibitem{ann237}
Announcement 237 (2015.6.18): A reality of the division by zero $z/0=0$ by geometrical optics.
\bibitem{ann246}
Announcement 246 (2015.9.17): An interpretation of the division by zero $1/0=0$ by the gradients of lines.
\bibitem{ann247}
Announcement 247 (2015.9.22): The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$.
\bibitem{ann250}
Announcement 250 (2015.10.20): What are numbers? - the Yamada field containing the division by zero $z/0=0$.
\bibitem{ann252}
Announcement 252 (2015.11.1): Circles and
curvature - an interpretation by Mr.
Hiroshi Michiwaki of the division by
zero $r/0 = 0$.
\bibitem{ann281}
Announcement 281(2016.2.1): The importance of the division by zero $z/0=0$.
\bibitem{ann282}
Announcement 282(2016.2.2): The Division by Zero $z/0=0$ on the Second Birthday.
\bibitem{ann293}
Announcement 293(2016.3.27): Parallel lines on the Euclidean plane from the viewpoint of division by zero 1/0=0.
\end{thebibliography}
\end{document}







毎日新聞 2016年06月12日 11時24分
(現代数学社・3024円)
今、私たちは、数学というと、ひどく難解な定理だの、公理だのを議論する、浮世離れした学問のように考えていないでしょうか。高校生が自分の将来を考える際にも、まず数学への親しみがあ…http://mainichi.jp/auth/guide.php?url=%2Farticles%2F20160612%2Fddm%2F015%2F070%2F003000c
物理学・数学は1600年代に急激に発展したというグラフ
Tuesday, October 13, 2015, 12:00 PM
10/13 晴 10時 浅草での空間線量は18ベクレル/立法メートル
「数学記号の誕生」(ジョセフ・メイザー著 松浦俊輔訳 河出書房新社 2014)
数学史の本では昨年出版された新しい本です。
体育の日はこれを読んでいました。
これは現代私たちが高校時代に悩まされた、あの忌まわしい(笑)微分積分記号や二次方程式とか、それよりもアラビア数字(0,1,2,3,4,5・・・)がどのように世界に定着していったのかを記した本です。
2500円もしますが、その価値はあるなあ。
最初は訳が固すぎて頭に入りませんが、世界史と数学史を一緒に勉強できるのでお得です(笑)
だいたいこのアラビア数字というやつはアラビア発祥ではありません。
ヒンドュー教のサンスクリット文字とペルシャ地方の文字が商業で用いるために発生したのが、現代のアラビア数字の原型です。
アラブを旅行した方はおわかりですが、中近東ではアラビア数字はほとんど目にしません。
空港で両替したお札から、バスや電車の時刻表はすべてアラビア<語>の数字です。なじみのない数字の記法なので「世界の歩き方(アラブ編)」の解説をひとときも離さずに、ひたすら解読するはめになります。
コインがいくらするのもわからないので、適当にコインを渡したらボーイが宙返りするような勢いで喜んでました。
あとで知ったのですが、最高額だったらしく(当時で500円ほど)、日当にあたるほどなんだとか。以後注意して渡すようにしました。
アラビア数字は本来ならばインド数字と呼称すべきなのですけども、インドとイスラム圏の交易で使われたためにアラビア数字と商人で使われたのが、呼称の始まりなのでいたしかたないかもしれません。
1200年頃になってアラビア数字はヨーロッパでも使われ出した
ローマ数字(Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ・・・)は計算には不便で、またゼロもないので商取引でははなはだ不便です。
そこでゼロという<位取りの記号>を用いた記述がヨーロッパの商人も使い出したのです。
この便利な数字をヨーロッパに紹介したのが、フィボナッチ(1170-1250頃)というイタリアの数学者がリベル・アバチという書籍で紹介して広く知られるようになりました。
フィボナッチというと、ウサギのつがいが毎月子供を産んでいくと一年後には何匹になるかというよく知られた算術問題で有名です。高校でもフィボナッチ数列という名前で教科書に載っていますね。
フィボナッチさんはイタリア商人の息子なので、貿易で使われる数字になじみがあったのですね。インド数学には10進数で位取りには0をつけるだけで良いために、筆記計算に適していることを認めて紹介したのです。
ギリシャやローマでは百千万という数詞が日本と同様にあり、そろばんでは良くても大きな数字を計算には手間がかかって不便だったからです。じっさいに0を使わないで、筆算すると、そのめんどくささは実感できるでしょう。
さあ、ヨーロッパに数字を使った解決方法(代数という数字だけの算術方式)が導入されると、爆発的に数学が進歩しました。
それまでは幾何学(天文学)という図形、つまり定規とコンパスだけで解くことが数学の能力であったし、それはキリスト教聖職者たちの秘技でもありました。
「異端の数 ゼロ 数学・物理学が恐れるもっとも危険な概念」(林大(はやしまさる)訳 早川書房 2003) ではゼロと無限という概念はキリスト教では考えてはいけないという考えであったので、インドで0が使われてもヨーロッパでは300年も使われずにいたのです。
1400年までは「+-×÷√」という算術記号はなかった
数学者といっても数式をだらだら書くことはなく、文章で書いてます。
だから数学者は神学者でもあり文学者でもあったのです。
数学が嫌いになる理由が数学記号と数字ばかりの字面だと思います。
なぜなら私も大嫌いでしたし、吐き気とめまいを覚えましたから。
ただ学生時代に同級生が、ナビエストークス方程式などを眺めてつぶやいた一言が「・・・美しい」でしたから、文学的な要素が多分にあることは認めますし、数学を専攻する人は式に芸術性を求める傾向が強いのだとか。
1400年以前に生まれていたら、きっと理系科目の数学や物理が好きになれたのにと思います。
機械時計の発明が物理学・天文学・航海術を飛躍させた
1675年に機械式時計がオランダの天文学者、ホイヘンスによって発案されたことが物理学を発展させたのです。
それまでの物理や数学は、幾何学(図形を用いた解決法)と代数学(数式を用いた解決法)です。
そこに時間という概念が加わって、物理運動(地球や太陽、月などの運行)がだんだんわかってきました。
それまでは時刻は月の満ち欠きと日の出日の入りで測るしかなかったからです。
ところが月の周期も日照時間も一定ではありません。農業ではこれでも良かったのでしょうが、測る物差しにはなり得なかったのです。
天文観測で不可欠な時間計測ができるようになって、運動の解析が1600年代後半から飛躍的に発展しました。
ゼロや無限に限りなく近い「極限」という概念が物理学を生み出した
ニュートンとライプニッツが微分積分という算術を発案して、これがすごい成果を生み出していきます。
ゼロであってゼロじゃない、無限であって無限でないが、とにかく果てしない先の値という<ごまかし>でゼロ/無限を忌むキリスト教会を騙して(なだめて)、あらたな微分積分という<宗教>概念を発表していきます。
ええ、微分積分はキリスト教の新宗派だったのです。無限とゼロに神が宿ると半分本気でニュートンは考えたのではないでしょうか。
1600年1700年あたりの科学知識が、我々が中学、高校で習った覚えのある数学や物理です。
そして意外と私を悩ました数学や物理は、中世以降で急激に発達した学問であることがわかります。
「数学記号の誕生」(ジョセフ・メイザー著 松浦俊輔訳 河出書房新社 2014)からグラフを掲載しておきます。
このグラフを眺めると、発展の度合いが冪状(べきじょう:急激に立ち上がるグラフ)であることがわかります。
ゼロが使われ出して、数式での計算が一般化すると(それまではすべて文章で記述されていた)、連立方程式やら、その解で小数点やマイナス、虚数という概念が生まれ、数字自体でも無理数(分数や有限な小数で表せない数、例では円周率π)の研究が進みました。
この急激な数学の発展にはワオと声を上げずにはいられませんね。
鎖国下の日本でも<なぜか>この潮流に追随するかのように数学は発展した!?
この先には先のノーベル賞を受賞した素粒子、ニュートリノの世界があるのです。 異端の数 ゼロ 数学・物理学が恐れるもっとも危険な概念 (2)
Tuesday, October 6, 2015, 03:05 PM
10/6 晴 10時 浅草での空間線量は33ベクレル/立法メートル
「異端の数 ゼロ」(林大 早川書房 2003)を読了しました。
前半はゼロが中世になって西洋キリスト教圏に受入れられるまでの過程とその後
後半は現代物理学・天文学においてもアインシュタインらがゼロという特異点に苦しんだ過程です。
西暦1500年あたりまでは、ローマおよび周辺キリスト教国ではゼロは触れてはならない数であったのです。
古代エジプトから発生した幾何学(測量や建築、暦)はギリシャに広がりましたがゼロは生まれませんでした。
バビロニア地方(ペルシャ、今の紛争が絶えない中近東)にはそろばんの空の桁を表す表記はありました。
マヤ人は日時がゼロから始まる独自の暦を持っていました。21世紀の最初の年は2000年なのか2001年なのかという大論争がありましたが、この暦であればそんな問題もなかったのです。
不幸なことに現代の暦はゼロのないエジプト人そしてローマ人がつくったものです。
ギリシャ人はその宇宙観からとことんゼロを嫌った
なぜならギリシャ教の神は「比率」だったからです。いわゆる黄金比などと呼ばれている比が奥義です。ギリシャ教の指導者はご存じピタゴラス!
急進で過激な思想家です。エジプトの幾何学から形に神の意志があると信じ、数学と図形は同じ意味とされていました。
だから定規とコンパスで計算することが奥義とされていましたし、宇宙も幾何学的な構造をもつと信じられていました。弦の振動や黄金比といったものが真理であったのです。
だからゼロという概念がないという宇宙観がギリシャ哲学であったのです。
ギリシャとペルシャで戦争が起こり、ペルシャ数学がギリシャにも伝わると、ギリシャ哲学者は頭を悩ますことになります。
たとえばゼノンの「アキレスと亀(アキレスのパラドックス)」・・・極限というゼロに近づける概念です。
やがてアルキメデスがギリシャに誕生し、王冠を壊さずに金がまがい物を知る方法や、細分割して放物線の面積を求める方法などを発見していきますが、不幸にも侵攻したローマ兵に殺されてしまいました。
こうしてローマはゼロを受入れることなく、時が流れてしまいました。
それではゼロはどちらに向ったかというと、西のヨーロッパではなく、東に流れ、インドやアラブ世界で大活躍します。
ヒンデゥー教では「無」は重要な概念です。アラブではアラビア数字となり、古代ユダヤ教においては数字に意味があるという神秘主義であり、ゼロも意味ある数と受入れられました。
時が流れて、キリスト教圏もイスラム圏と貿易をする上でゼロは欠かせなくなります。イタリア商人らが計算に便利なアラビア数字を使い出したのが1200年頃、そして実用的なので教会は反対しつつも、アラビア数字はヨーロッパで受入れられていきます。
ゼロを異端とするカトリックとルネサンスで花咲く数学・美術
ヨーロッパの哲学論争には「無」と「無限」が論争の種となりました。
美術では遠近法(無限遠は一点に集まるという手法)、天文学ではアリストテレスの天動説からプトレマイオスの地動説へ、そしてコペルニクスの現代の太陽系モデルの提唱、そしてケプラー、ニュートンといった修道士たちがぞくぞくとカトリックの宇宙観へ反旗を翻していきます。
無と無限を否定するイエズス会にもデカルトが座標を用いることで幾何学が代数に融合できることを発見します。
ニュートン、ライプニッツが「微小」の概念を取り入れて微分積分という強力な概念を構築します。
フランス革命頃になると、果てしなく永遠と続く式も考えられるようになります。級数という概念ですね。
微分積分という新しくて強力な道具を手に入れた数学者達は、どんどん不可侵と思われていた領域へ斬込んでいきます。
18世紀にはマクローリン、テイラーというイギリスの数学者は無限に続く式も、収束するという概念を確立します。
19世紀にはガウスが虚数という概念を用いると、多次元の式でも解を求めることができることを発表します。デカルト座標が複素平面という不思議な面へと数字の世界が拡大していきます。
デカルト平面では直線でも、複素平面では円となります。さらに3次元の複素空間では球となります。
直線の運動も複素数の世界では球面の動きになる
リーマンはゼロと無限とは複素数の世界では、ちょうど地球儀の極点となることに気づきます。
こうして19世紀あたりで数学者達はゼロと無限の概念を掴みつつありました。
このゼロと無限の概念は物理学へと移り、ブラックホール理論やビッグバンという宇宙の構造をしらべる手段へと進化していくのです。
どちらも「ゼロ」という特異点、ブラックホールは重力が一点に集まったら、ビッグバンは宇宙の始まりのゼロ秒はどうであったのかを考え抜いた末の概念です。
ブラックホールの存在は確認されていますが、ビッグバンは調べようがありません。
宇宙が膨張しているという説は最近では揺れ動いています。
このように本書は非常に壮大なゼロの物語です、そして残念ながらまだ未完です。
これからもゼロに注目していきましょう。生きているうちに新たな発見がされるかもしれません。
過去ログ:異端の数 ゼロ 数学・物理学が恐れるもっとも危険な概念 (1) http://www.rokujo-radium.com/blog/?entry=entry151013-120049
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 300: New challenges on the division by zero z/0=0\\
(2016.05.22)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
%\date{\today}
\maketitle
{\bf Abstract: } In this announcement, for its importance we would like to state the
situation on the division by zero and propose basic new challenges.
\bigskip
\section{Introduction}
%\label{sect1}
By a {\bf natural extension} of the fractions
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, we found the simple and beautiful result, for any complex number $b$
\begin{equation}
\frac{b}{0}=0,
\end{equation}
incidentally in \cite{s} by the Tikhonov regularization for the Hadamard product inversions for matrices and we discussed their properties and gave several physical interpretations on the general fractions in \cite{kmsy} for the case of real numbers.
The division by zero has a long and mysterious story over the world (see, for example, Google site with the division by zero) with its physical viewpoints since the document of zero in India on AD 628, however,
Sin-Ei Takahasi (\cite{kmsy}) established a simple and decisive interpretation (1.2) by analyzing the extensions of fractions and by showing the complete characterization for the property (1.2):
\bigskip
{\bf Proposition 1. }{\it Let F be a function from ${\bf C }\times {\bf C }$ to ${\bf C }$ satisfying
$$
F (b, a)F (c, d)= F (bc, ad)
$$
for all
$$
a, b, c, d \in {\bf C }
$$
and
$$
F (b, a) = \frac {b}{a }, \quad a, b \in {\bf C }, a \ne 0.
$$
Then, we obtain, for any $b \in {\bf C } $
$$
F (b, 0) = 0.
$$
}
Note that the complete proof of this proposition is simply given by 2 or 3 lines.
\medskip
We thus should consider, for any complex number $b$, as (1.2);
that is, for the mapping
\begin{equation}
w = \frac{1}{z},
\end{equation}
the image of $z=0$ is $w=0$ ({\bf should be defined}). This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere. Therefore, the division by zero will give great impacts to complex analysis and to our ideas for the space and universe.
However, the division by zero (1.2) is now clear, indeed, for the introduction of (1.2), we have several independent approaches as in:
\medskip
1) by the generalization of the fractions by the Tikhonov regularization or by the Moore-Penrose generalized inverse,
\medskip
2) by the intuitive meaning of the fractions (division) by H. Michiwaki,
\medskip
3) by the unique extension of the fractions by S. Takahasi, as in the above,
\medskip
4) by the extension of the fundamental function $W = 1/z$ from ${\bf C} \setminus \{0\}$ into ${\bf C}$ such that $W =1/z$ is a one to one and onto mapping from $ {\bf C} \setminus \{0\} $ onto ${\bf C} \setminus \{0\}$ and the division by zero $1/0=0$ is a one to one and onto mapping extension of the function $W =1/z $ from ${\bf C}$ onto ${\bf C}$,
\medskip
and
\medskip
5) by considering the values of functions with the mean values of functions.
\medskip
Furthermore, in (\cite{msy}) we gave the results in order to show the reality of the division by zero in our world:
\medskip
\medskip
A) a field structure containing the division by zero --- the Yamada field ${\bf Y}$,
\medskip
B) by the gradient of the $y$ axis on the $(x,y)$ plane --- $\tan \frac{\pi}{2} =0$,
\medskip
C) by the reflection $W =1/\overline{z}$ of $W= z$ with respect to the unit circle with center at the origin on the complex $z$ plane --- the reflection point of zero is zero,
\medskip
and
\medskip
D) by considering rotation of a right circular cone having some very interesting
phenomenon from some practical and physical problem.
\medskip
In (\cite{mos}), many division by zero results in Euclidean spaces are given and the basic idea at the point at infinity should be changed. In (\cite{ms}), we gave beautiful geometrical interpretations of determinants from the viewpoint of the division by zero. The results show that the division by zero is our basic and elementary mathematics in our world.
\medskip
See J. A. Bergstra, Y. Hirshfeld and J. V. Tucker \cite{bht} for the relationship between fields and the division by zero, and the importance of the division by zero for computer science. It seems that the relationship of the division by zero and field structures are abstract in their paper.
Meanwhile, J. P. Barukcic and I. Barukcic (\cite{bb}) discussed recently the relation between the divisions $0/0$, $1/0$ and special relative theory of Einstein. However, their logic seems to be curious and their results contradict with ours.
Furthermore, T. S. Reis and J.A.D.W. Anderson (\cite{ra,ra2}) extend the system of the real numbers by introducing an ideal number for the division by zero $0/0$.
Meanwhile, we should refer to up-to-date information:
{\it Riemann Hypothesis Addendum - Breakthrough
Kurt Arbenz
https://www.researchgate.net/publication/272022137 Riemann Hypothesis Addendum - Breakthrough.}
\medskip
Here, we recall Albert Einstein's words on mathematics:
Blackholes are where God divided by zero.
I don't believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} [1]:
1. Gamow, G., My World Line (Viking, New York). p 44, 1970.
For our ideas on the division by zero, see the survey style announcements 179,185,237,246,247,250 and 252 of the Institute of Reproducing Kernels (\cite{ann179,ann185,ann237,ann246,ann247,ann250,ann252,ann293}).
\section{On mathematics}
Apparently, the division by zero is a great missing in our mathematics and the result (1.2) is definitely determined as our basic mathematics, as we see from Proposition 1. Note its very general assumptions and many fundamental evidences in our world in (\cite{kmsy,msy,mos}). The results will give great impacts on Euclidean spaces, analytic geometry, calculus, differential equations, complex analysis and physical problems. See our announcements for the details.
The mysterious history of the division by zero over one thousand years is a great shame of mathematicians and human race on the world history, like the Ptolemaic system (geocentric theory). The division by zero will become a typical symbol of foolish human race with long and unceasing struggles. Future people will realize this fact as a definite common sense.
We should check and fill our mathematics, globally and beautifully, from the viewpoint of the division by zero. Our mathematics will be more perfect and beautiful, and will give great impacts to our basic ideas on the universe.
\section{Albert Einstein's biggest blunder}
The division by zero is directly related to the Einstein's theory and various
physical problems
containing the division by zero. Now we should check the theory and the problems by the concept of the RIGHT and DEFINITE division by zero. Now is the best time since 100 years from Albert Einstein. It seems that the background knowledge is timely fruitful.
\section{Computer systems}
The above Professors listed are wishing the contributions in order to avoid the zero division trouble in computers. Now, we should arrange new computer systems in order not to meet the division by zero trouble in computer systems.
\section{General ideas on the universe}
The division by zero may be related to religion, philosophy and the ideas on the universe, and it will creat a new world. Look the new world.
\bigskip
We are standing on a new generation and in front of the new world, as in the discovery of the Americas.
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{bb}
J. P. Barukcic and I. Barukcic, Anti Aristotle—The Division of Zero by Zero. Journal of Applied Mathematics and Physics, {\bf 4}(2016), 749-761.
doi: 10.4236/jamp.2016.44085.
\bibitem{bht}
J. A. Bergstra, Y. Hirshfeld and J. V. Tucker,
Meadows and the equational specification of division (arXiv:0901.0823v1[math.RA] 7 Jan 2009).
\bibitem{cs}
L. P. Castro and S. Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ms}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$,
Linear Algebra \& Matrix Theory (ALAMT)(to appear).
\bibitem{msy}
H. Michiwaki, S. Saitoh, and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{mos}
H. Michiwaki, H. Okumura, and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces.
International Journal of Mathematics and Computation
(in press).
\bibitem{ra}
T. S. Reis and J.A.D.W. Anderson,
Transdifferential and Transintegral Calculus,
Proceedings of the World Congress on Engineering and Computer Science 2014 Vol I
WCECS 2014, 22-24 October, 2014, San Francisco, USA
\bibitem{ra2}
T. S. Reis and J.A.D.W. Anderson,
Transreal Calculus,
IAENG International J. of Applied Math., {\bf 45}(2015): IJAM 45 1 06.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\bibitem{ann179}
Announcement 179 (2014.8.30): Division by zero is clear as z/0=0 and it is fundamental in mathematics.
\bibitem{ann185}
Announcement 185 (2014.10.22): The importance of the division by zero $z/0=0$.
\bibitem{ann237}
Announcement 237 (2015.6.18): A reality of the division by zero $z/0=0$ by geometrical optics.
\bibitem{ann246}
Announcement 246 (2015.9.17): An interpretation of the division by zero $1/0=0$ by the gradients of lines.
\bibitem{ann247}
Announcement 247 (2015.9.22): The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$.
\bibitem{ann250}
Announcement 250 (2015.10.20): What are numbers? - the Yamada field containing the division by zero $z/0=0$.
\bibitem{ann252}
Announcement 252 (2015.11.1): Circles and
curvature - an interpretation by Mr.
Hiroshi Michiwaki of the division by
zero $r/0 = 0$.
\bibitem{ann281}
Announcement 281(2016.2.1): The importance of the division by zero $z/0=0$.
\bibitem{ann282}
Announcement 282(2016.2.2): The Division by Zero $z/0=0$ on the Second Birthday.
\bibitem{ann293}
Announcement 293(2016.3.27): Parallel lines on the Euclidean plane from the viewpoint of division by zero 1/0=0.
\end{thebibliography}
\end{document}








0 件のコメント:
コメントを投稿