再生核研究所声明 466 (2019.1.2): 不完全な 現代初等数学、数学の基礎
そもそも数学とは、算術の四則演算を基礎に 組み立てられていると言える。なるほど
世界最初の本格的な学術書ユークリッド原論では厳格に四則演算が確立され、展開されていたとは言えないが ピタゴラスの定理、比の重要な概念やユークリッド互除法、アルキメデスの放物線で囲まれた面積の求積などから 数の認識は相当に 深いと言える。ところが既にユークリッドの先人、アリストテレスは 物理的な概念から、ゼロで割ることは不可能であると主張され、現代でもギリシャ文化の強い影響を受けている、欧米の文化圏では 相当にゼロを嫌い、ゼロ除算に拒否反応が 強い。
他方、ゼロを発見して 算術の法則を確立した インドのBrahmagupta (598 -668?) はその際に 既にゼロ除算0/0=0 を正しく述べ、その後数百年に亘って、インドではゼロ除算 1/0 を問題にして、何と現在でも世界で10人くらいが追究している数学愛好者、数物、計算機関係の研究者たちが存在する。1/0 について、奇怪な数を考えたり、それらを含める理論体系を模索している状況すら存在する。
ゼロ除算でまず、触れるべきことは、ゼロ除算は不可能である という、数学界の永い間の定説と、アインシュタインの言葉に代表されるように、ゼロ除算は、物理学上の懸案の問題である という状況である。すなわち、ゼロ除算を普通の除算のように 掛け算の逆で考えれば、ゼロ除算が不可能であることは 直ちに証明されてしまうので、数学的に議論の余地は 無くなってしまう。 他方、物理学などでは 分数で公式が表現される基本法則が数多く存在するが、それらの公式で 分母がゼロの場合の意味づけが問われ、ゼロ除算が本質的な問題を引き起こす。 - ブラックホールは 神がゼロで割ったところに存在するなどと、神秘的な表現が出回っている。
ところが、ゼロ除算は意外な展開を見せた。1/0 の意味が問題であった と言える。1/0 そのものは意味がないから、関数f(z)= 1/z で z がゼロに近づいた先に定義されると 人は理解して、殆どの人々は今でもそう考えて、結果として 無限、あるいは 無限のようなもの であると考えている。実数の世界で、考えれば プラス、マイナス無限大と考えるだろう。ところが、拡張分数や代数的構造、一意性の概念、自然性からその基本関数の原点での値は ゼロとすべきことが、沢山の実例から発見された。数学的に表現すれば、解析関数f(z)のz=0での値を 近くでの近づく値、極限の考えで考えてきたが、特異点z=0 での値は、不連続的に 値0 を取っているという発見である。 そもそも数学では、特異点自身では 考えず、 何時も特異点を除いた近傍で 解析関数を考えて来たという事実である。原点で特異性を許す 原点での近傍で解析的な関数F(z)に対して、 関数F(z)/z の原点での値が 何時でも有限確定値として定まるという、ゼロ除算算法 が発見された。それが我々の発見した、ゼロで割れるという、我々の意味である。従来考えない 考えてはならない 特異点での関数値が考えられる というのであるから、この考えは 全く新しい世界、数学である と言える。- 特異点の周りではなく、特異点そのもので 我々は数学が考えられる。 その意味で、特異点で考えない数学は、不完全であり 一部の世界を論じているに過ぎない と言える。この意味で、未だ数学は不完全である と言える。
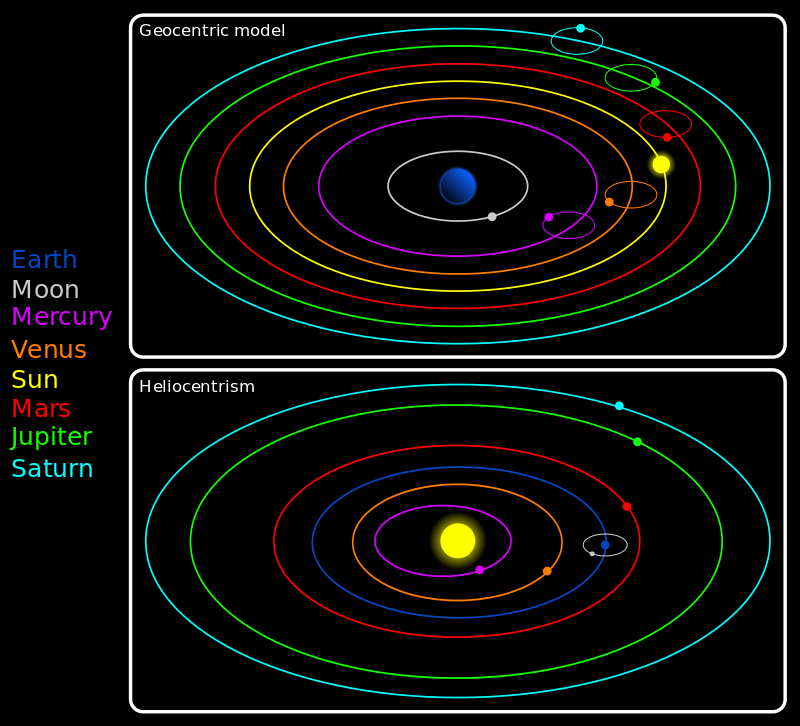
今まで考えなかった、ゼロで割る問題は、明確な意味で ゼロで割れて、初等数学全般に広範な影響を与え、ゼロ除算の知見は 現在900件を超え、ユークリッド幾何学、解析幾何学、微積分学、微分方程式論、複素解析学 など 初等数学全般に及んでいる。典型的な例として、無限遠点がゼロで表されること、\tan(\pi/2) =0, いわゆるy軸の勾配はゼロであり, \exp(1/z) は 原点で、ピカールの除外値 1の値を取っていることが挙げられる。直線の性質、三角形、三角関数の公式、円や2次曲線諭などにも 沢山の欠陥が発見された。勾配の概念や微分法の概念すら不完全である と言える。初等数学全般の修正、補充は 美しい数学の体系には避けられない。関係学術書は言わば穴だらけで、欠陥に満ちている と言える。 ゼロ除算算法は、ゼロと無限の関係を明らかにして、単に数学を超えて 天動説の変更や進化論のように 世界観の変更を齎し、新たな夜明け、時代を招くだろう。
以 上





























































0 件のコメント:
コメントを投稿