「興味のある科学の分野に関するアンケート」実施、子どもが科学分野に興味をもったきっかけは「実物を見て」
アクトインディが企画運営する子どもとお出かけ情報サイト「いこーよ」は、12歳以下の子どもを持つ保護者247名を対象に実施した、「興味のある科学の分野に関するアンケート」の結果を9月25日に発表した。
「興味のある科学の分野に関するアンケート」は、全国の12歳以下の子どもを持つ保護者を対象に9月3日~18日の期間に実施され、247名から有効回答を得ている。
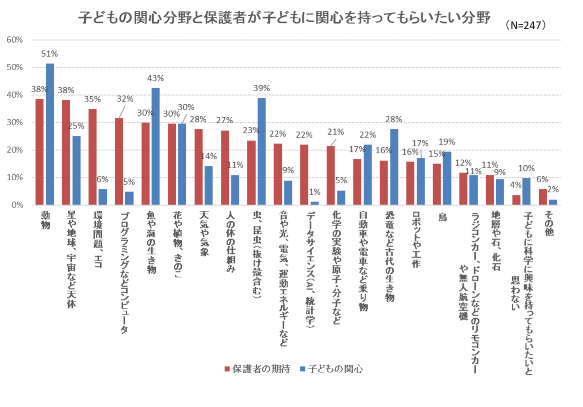
子どもの科学に対する関心分野を尋ねたところ、上位5位までが生き物に関する分野となった。一方で、「プログラミング」や「AIなどのデータサイエンス」といった新しい分野は、調査対象が12歳以下だったこともあり、それほど関心は高くない。
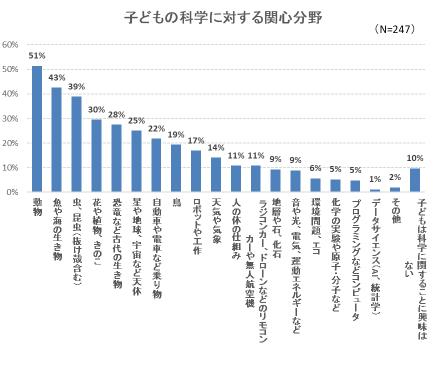
男女別では、「鳥」や「動物」では差がほぼないものの、「花や植物」は女の子、「虫、昆虫」「魚や海の生き物」は男の子の関心が高い。また、「恐竜など古代の生き物」「自動車や電車など乗り物」「ロボットや工作」「ラジコンカー、ドローンなどのリモコンカーや無人航空機」の分野は女の子はそれほどでもないが、男の子の関心は際立って高かった。
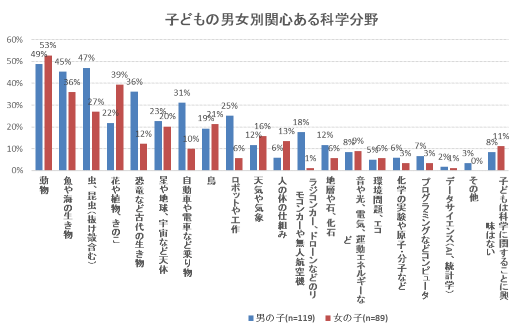
現在関心のある科学分野に興味をもったきっかけを尋ねた質問では、「動物園や水族館、博物館などで実物を見て」「公園、海、山などの外遊びを通して」などが上位となっており、自然体験や実物を見られる施設での体験を通して、多くの実物に触れさせることが、科学への関心を深める最初の一歩となっていることがわかる。また、「テレビ番組を見て」も上位になっており、画像や動画が豊富に使われ、親しみやすく解説されたテレビ番組が、科学への関心を高めることに一役買っているといえる。
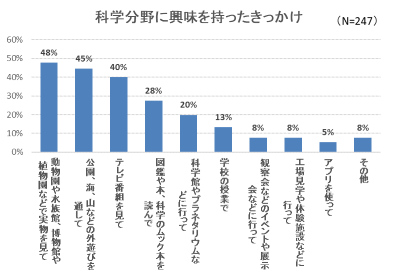
科学に触れるイベントや施設へ行ったことがあるかを尋ねたところ、行ったことがある子どもの方が行かない子どもよりも科学分野に関する関心が高く、「行かない」子どもの18%は「科学に関することに興味はない」と答えている。
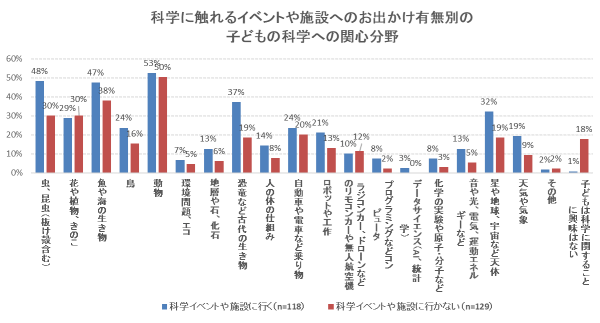
保護者に対して関心のある科学分野を尋ねた質問では、子どもの関心が生き物分野に寄っているのに対して、「天体」「天気や気象」「人体」「環境問題、エコ」など多岐にわたる。
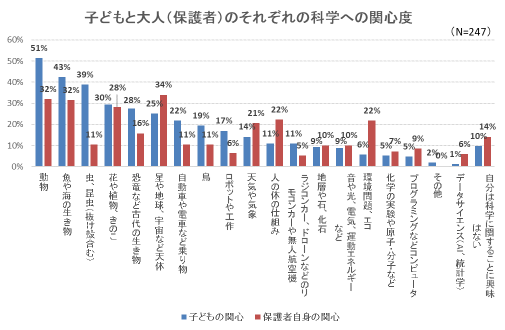
保護者が子どもに関心を持ってもらいたいと思っている科学分野としては、「環境問題、エコ」(3位)、「プログラミング」(4位)が上位になったほか、AIなどデータサイエンスも非常に多かった。一方で、ドローンなどは世間で話題になっているにも関わらず、低い結果となっている。
ゼロ除算の発見は日本です:
∞???
∞は定まった数ではない・
人工知能はゼロ除算ができるでしょうか:
とても興味深く読みました:2014年2月2日 4周年を超えました:
ゼロ除算の発見と重要性を指摘した:日本、再生核研究所
ゼロ除算関係論文・本
再生核研究所声明 452 (2018.9.27): 世界を変えた書物展 - 上野の森美術館
(2018年9月8日―24日 )
2018.9.17. 展示書籍などを拝見させて頂きました。大変賑わっていて関心の大きさが感じられました。時間の関係で じっくり、詳しくとは行きませんでしたが、全体の案内(知の連鎖ゾーン)で、初期、初めにアリストテレスとユークリッドが 在って、中間くらいにニュートン、最後がアインシュタインで 世界史を壮観する想いがしました。 数学では 非ユークリッド幾何学の扱いにおけるガウスの記述、資料の欠落と算術の発見、ゼロの発見の Brahmagupta (598 -668 ?) の欠落は 残念に思われました。書籍など無くても大事な事実と思いますので、 大きく取り上げて欲しかった。
この世界史年表で凄いことに気づいて興奮して後にしました。
ゼロ除算がこれらで基本的な関与があるからです。
まず、ゼロ除算は、ユークリッド幾何学の変更を求め、連続性のアリストテレスの世界観に反して、強力な不連続性の世界を示しています。ゼロ除算はアインシュタインの人生最大の関心事であったとされ、今でもなお、ゼロ除算とアインシュタインの相対性理論との関係が議論され、ブラックホールは 神がゼロで割ったところに存在するなどと 神秘的な問題を提供しているからです。
もちろん、Brahmaguptaは ゼロ除算を議論していて、その後、1300年に亘って、世界史で議論されてきて、 ニユートン力学でも基本的な問題を提起している。 当然、非ユークリッド幾何学とも関係していて、それらの空間とも違う全く新しい幾何学を提案している。このように考えると、検討中の Division by Zero Calculus の著書(出版契約済み)は 世界史上で大きな扱いになるだろうと発想して、大変興奮して、展示会を後にしました。
広く世界に意見を求め、この著書の出版計画を進めたい。 そのためにも途中経過も公表して行きたい。
ところで、 展示会の名称には 世界を変えた科学の書物展示会などと、 科学などの言葉を加える必要があるのではないでしょうか。 そうでなければ、 バイブル、法華経、コーラン、論語などが並ぶことになるのでは ないでしょうか。
尚、ゼロ除算については、一般向きには
http://www.mirun.sctv.jp/~suugaku/
○ 堪らなく楽しい数学-ゼロで割ることを考える
○ 堪らなく楽しい数学-ゼロで割ることを考える
で4年間を越えて解説を続けています。
最後に素晴らしい展示会を企画され、そのために努力された人たちに 敬意と感謝の気持ちを表明したい。
以 上
再生核研究所声明 401(2017.11.18): 数学の全体、姿、生命力ここ一連の声明で数学について述べてきた:
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
No.81, May 2012(pdf 432kb) - International Society for Mathematical ...
www.jams.or.jp/kaiho/kaiho-81.pdf
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れ、違った観点から、数学の本質論と社会への影響について述べた。さらに
数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ人にとっては価値がないものであるとも言える。― もちろん、逆に、未来人が高い評価を与える場合もある。
この文脈で数学の全体と生命力について言及して置きたい。数学とは、時間にもエネルギーにもよらない関係の全体であるから、数学的な論理思考を備えた高度な人工知能が自動的に数学を発展させていく可能性を否定できない。初歩的な数学では、実際、そのような試みがなされているという。人間を離れた、数学の全体像はどのようになるだろうか。基本的な仮説の上に何でも考えて、- これはいろいろな場合に当たって 何でも試行していく方法がとられるだろう。- しかしながら、人工知能が新しい概念や、定義を与えられるかは本質的な問題ではないだろうか。このような思いで数学の全体像を想像すると、基本的な仮定からどんどんいろいろな関係を導き、それは大樹のような姿に成るのではないだろうか。数学の客観的な存在はそのようであると考えられる。
ところが現在数学は人が展開して、発展させている状況から、数学の発展は 人間によるという現実がある。数学の客観的な在りように人間が関与してくる。そこで、関与する人間の興味と関心でどんどん進む状況と他からの要請でどんどん進む方向が存在する。後者は位置づけが明瞭であるが、前者の純粋数学の発展の様は大いに注目される。共通的な興味、関心で研究者の多い分野が存在し、いわゆる権威ある者の影響で門下生が多く、深く研究が進む状況は良くみられる。有名な難問に挑戦する相当な研究者集団も顕著である。数学にもブームや流行が有って、ある時期、相当に流行って研究会などで大きな話題になった話題が20年や30年くらい経つと関与する研究者が殆どいなくなってしまう状況がみられる。
それで、数学が大きな生命力をもって発展する華やかな時代と、細分化が進み、他との関係、他に影響や関心を与えない程になって、衰退していく、いわば大木では幹の部分から小さな枝や葉の部分になって数学は終末を迎えるのではないだろうか。数学は時間やエネルギーにもよらない不変なものであるが 数学の担い手である、人間に関与していて、人間が命ある生命であるように 数学も人間の影響を受けていると考えられる。
その意味で純粋数学者は、現在の 数学の位置づけ と 自分の心 をしっかりと捉えることが大事ではないだろうか。
以 上
再生核研究所声明 400(2017.11.17): 数学の研究における喜びと嫌な思い
人間生きて居れば楽しいとき、苦しいとき、感情の起伏は避けられない。人間の感情は絶えず揺れ動くものである。数学の研究におけるそのような感情の起伏を回想しながら纏めてみたい。
研究の初期であるが、何を研究するか、研究課題の選択は非常に難しく一般には研究生活における苦しい時期ではないだろうか。もちろん好きだから数学を専攻したのだから、学んでいるときには新しい世界がどんどん広がって、楽しいが、新しい結果を得るには一般には容易なことでないと言える。広く深い現代数学において研究課題の選択は研究者の将来を相当に定めることになる。一般には好きな分野での好きな指導教授の数学の範囲での選択に成る。そこで、何か新しいことを発見、解決して、論文を出版することが大事な目標になる。論文を出版する事は博士号の取得や研究職に付くための条件に成るから、何が何でも論文を書くが 直接の目標になる。この時、手っ取り早い方法は提起されている問題を解決したり、読んだ論文の内容の一般化、精密化、類似の理論の展開などであるが、それらとて甘くはなく、いずれもそれぞれの専門家が出来なかったこと、気づかないことの発見、新規な展開だから、研究は厳しく、研究の初期は誠に厳しいものであると考えられる。- 数学を志す者にはいわば優秀な人が多く、難なくここを踏破していく者も多い。しかし、簡単に踏破していくような人は行き詰る場合も多く、苦労して研究課題を自分に合ったように選択した者は、最初は遅れても永く研究が続く面もあるようである。- この観点からは、早期の成果を期待し過ぎの風潮は問題があるのではないだろうか。何事初期の取り組みが大事なようである。専門化、高度化の厳しい現代数学、簡単には研究課題は変えられず、生涯の研究の方向は 多くは初期で決まっている現実があると考えられる。― これは何でも飛び越えていくような天才的な人を想定しているのではなく、一般的な数学者を想定している。
1つの研究課題で論文が連続的に書けるような時代に入れば、充実した研究生活で、創造活動ができる輝ける時代を歩めるのではないだろうか。新しい考えが湧いたとき、思わぬことを発見したとき、またそのような予感がする時は 研究者の充実しているときであると言える。良い考えが湧いたときなど、眩暈がするほどの喜びが湧き、それは苦しいほどであると表現できる。発見の瞬間、得た結果の評価に対する共感、共鳴は人間の最高の喜びの類に入るだろう。評価が違って共感が得られなかったり、論文執筆上の形式的な気遣いは研究生活における影の部分に成るが、それが研究の芽に成るので、苦しみも喜びの内と考えるべきである。研究課題の行き詰まりもそうである。行き詰るから新しい芽が出てくるのである。苦しみと喜びは絶えず変化し、喜びも苦しみも区別がつかず、その活動が研究生活と言える。
若い研究者の博士号取得、就職、そしてパーマネントの研究職に付くまでの厳しさは回想しても苦しい、修業時代と言える。しかしそれらが、生涯の研究の基礎に成る。
所謂論文投稿から採否決定までの間、永さは 研究者にとっては一般に苦しい状態ではないだろうか。研究成果を評価に活かせないからである。その点、インターネットの普及で論文原稿をアーカイブなどで公開できるシステムには 格段の進歩と高く評価される。- 英文書き換え要求に対して 多くは1週間かけて 進んだIBM 修正機能付きの電子タイプライターで書き替え、原稿の送付と返事にさらに2週間掛ったが、現在は、修正は分単位、何回でも書き換えができて、連絡は1日で十分である。素晴しい時代を迎えていると言える。
研究者の嫌なこととは集中している折り、いろいろ雑用が入ることではないだろうか。一心不乱に研究に専念しているとき、それを乱されるとき、本能的に嫌がるのは自然な心で、心此処にあらずの状況は良き家庭人や良き親であることの余裕を失わせ、いろいろ良からぬ家庭問題や対人関係を作りかねないと憂慮される。大学の法人化後の日本の大学の多くが研究者の大事な自由な時間と余裕を失なわしめ、逆に雑用を多くして、研究者を虐待しているように感じられる。5年間ポルトガルの大学から研究員として招待され、研究に専念できたが、過ごした経験から、あまりにも大きな違いを感じて 唖然としている。
それから、数学の研究成果の発表では 間違いをおかしてはならないことは 相当に厳しい原則であるから、投稿したら、間違いがあった、出版済みの論文に間違いを発見した等の場合には、相当ショックで、相当に苦しい心理状況に追い込まれる。研究上の相当な時間は 繰り返し不備はないか、間違いはないかの省察の時間ではないだろうか。絶えず、大丈夫か、大丈夫か、間違いはないか、間違いはないかと自問していると言える。もちろん、理論の全体の在り様に対する想いは、真智への愛 である。
以 上
再生核研究所声明 399(2017.11.16): 数学芸術 分野の創造の提案 - 数学の社会性と楽しみの観点から
ここ一連の声明で数学について述べてきた:
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れ、違った観点から、数学の本質論と社会への影響について述べた。さらに
数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ人にとっては価値がないものであるとも言える。― もちろん、逆に、未来人が高い評価を与える場合もある。
そこで自然な考えが突然浮かんだ:
2017.11.13.10:45 突然、この流れで考えが湧いた。数学を芸術として楽しもうという新しい分野の創造の提案である。
数学は抽象的な理論、文章や式で表される場合が多く、社会の一般の方の理解が難しい不幸な状況にある。数理に興味を抱く多くの人々を遠ざけ、数理に喜びや楽しみがあるのに、スポーツやドラマ、芸術、文学などに比べて民衆の享受に寄与していないのは、数理の美しい世界の存在に比べて誠に残念な状況であると危惧される。― 数理の話題、ニュース、情報の極端に少ない現状からそう判断せざるを得ないのではないだろうか。数理科学を楽しみ、数理の世界の社会貢献、裾野の広がりを求めて、数学芸術 分野の創造と発展を提案したい。少し、具体的に触れるが いろいろな衆知を集めて構想そのものの進化を期待したい。
数学芸術は 数学の内容を、絵画やその他の手段で簡明な表現を求め、音楽や絵画が感動を呼び起すように 美しい表現を追求していく。
数理科学の社会的文化的基盤を拡充、充実発展させ、数理科学を芸術のように楽しみ、かつ 真智への愛 を育てる。
以 上
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
数学、数学の本質論については 次で相当深く触れた:
また数学の社会性の観点からは、
再生核研究所声明 392(2017.11.2): 数学者の世界外からみた数学 ― 数学界の在り様について
で触れた。少し、違った観点から、数学の本質論と社会への影響について述べたい。
数学とは関係の集まりであるが、時間にもエネルギーにもよらない数学の論理の神秘性から、神学のような性格を帯びていて、およそ世に絶対的という概念が有ればそれは数学くらいで 特別に尊い存在であると考えられてきた。ところが非ユークリッド幾何学の出現で、数学についての考えは本質的に変えられ、数学とは ある仮定系、公理系から論理的に導かれた関係の総体が その公理系から導かれた一つの数学で、数学自身は絶対的な真理や世の価値とは無関係な存在であるという認識に改められた。数学とは基本的に、ある仮定の下に導かれる全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになるが、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ価値がないものであるとも言える。― 近年 異常な評価時代に、論文、著書など、引用情報やダウンロード数などが重視される世相を作っている。現在は表面的なデータによる行き過ぎとしても、将来は相当に裏付けの伴う評価に発展して、評価は人工知能が活躍する分野に成るのではないだろうか。
この観点は、2014.2.2に発見されたゼロ除算とゼロ除算算法の研究姿勢に大きなヒントを与えてくれる。そもそもゼロ除算は1000年以上も不可能であり、考えてはいけない が 数学界の定説であった。それが全然予想もされなかった結果であったと報告されても、全く新しい数学で、世の常識と違うわけであるから、始めは、興味も、関心も抱かないのは当然とも言える。気づいてみれば、ゼロ除算は本質的には定義であり、仮定とも言えるので、上記数学の観点からは、新しい数学とも言える。そこで、ゼロ除算の世界を広く社会に紹介するために初等数学全般に亘ってゼロ除算の影響を調べてみることにした。新しい数学がどのような意義を有するかを問題にした。
誠に皮肉なことには、ゼロ除算の、ゼロ除算算法の直接の影響として、ユークリッド、アリストテレスの世界観を変える、結果を導くことである。始めから重大な問題を提起してきた。すなわち、無限遠点はゼロで表される、すべての直線には原点を加えて考えるべきである。― 異なる平行線は原点を共有するとなって、 ユークリッドの平行線の公理に反し、世の連続性に対するアリストテレスの世界観にも反することになる。さらに、円の中心の円に関する鏡像は無限遠点でなく、円の中心自身であるとなって、古典的な結果に反することになる。驚嘆すべきことに、x、y直交座標系で y軸の勾配は ゼロであるという結果をもたらす。すなわち、 \tan(\pi/2) =0 である。
それで、初等数学全般に大きな影響が出ることが明かになった。
大事な論理的な原理は、新しい定義、仮定からゼロ除算は展開されるので、得られた結果、導かれた結果については吟味を行い、結果について評価する態度が大事である。ところが考えてみれば、数学そのものが実はそうであった。数学も、得られた結果がどのような意味が、自分の好みを越えて価値があるか否かを絶えず吟味していきたい。吟味して行かなければならない。
以 上
再生核研究所声明 402(2017.11.19): 研究進めるべきか否か - 数学の発展
ここ一連の声明で数学について述べてきた:
再生核研究所声明 397(2017.11.14): 未来に生きる - 生物の本能
再生核研究所声明 398(2017.11.15): 数学の本質論と社会への影響の観点から - ゼロ除算算法の出現の視点から
再生核研究所声明 399(2017.11.16): 数学芸術 分野の創造の提案 - 数学の社会性と楽しみの観点から
再生核研究所声明 400(2017.11.17): 数学の研究における喜びと嫌な思い
再生核研究所声明 401(2017.11.18): 数学の全体、姿、生命力
数学の本質論については 次で相当深く触れた:
ここでは、現実の問題から、研究姿勢、路線について具体的に考察したい。
数学とは基本的に、ある仮定の下に導かれる関係の全体である。関与する数学者にとっては、その体系に魅せられ関係を追求していくことになる. しかし、他の人にとっては、あるいは社会的には、それらがどのような意味、影響を与えてくれるかが 人が興味、関心を抱くか否かが大事な問題であると言える。他からみれば、興味、関心、影響を与えないようなものは 存在していないようなものであるから、それだけ人にとっては価値がないものであるとも言える。― もちろん、未来人が高い評価を与える場合もある。また、
デカルトの円定理:
定理は3つの外接する円に対して、それらに内接する円と外接する円の半径を、3つの円の半径で表わす公式を与えたものであるが、その公式は美しい形を有している。ところで、円の半径がゼロならば、点円、半径が無限大ならば、直線になると考えられる。後者の解釈については、ゼロ除算算法の導入で、直線とは中心が原点、半径ゼロの円と見なせるという知見をもたらした。点も直線も円の1種であるという考えから、それではデカルトの美しい定理で、円を直線や点の場合にも成り立つかと考えた。ゼロ除算算法で、2つが円で1つが点以外は、そのまま成り立つことが確認され、この例外である場合に、驚嘆すべきことが分った。3つの円が接しているとき、デカルトの定理は成り立っている。そこで、1つを点に近づけ、点に成ったときにデカルトの定理がどうなるかを調べた。点のときは内接円も外接円も存在しないから、デカルトの定理は成り立たないと考えられる。ところが、点に成ったとき、ゼロ除算算法で解析すると、その点は3つの場合に突然、変化する現象が現れた。点以外に、美しい円が2つ現れる。これらの円について、デカルトの定理を成り立たせる解釈が存在することが分った。― 点が変化して、変化した円で、デカルトの定理が成り立っている。専門家 奥村博博士と論文を執筆中である(2017.11.5.6.57)。この予稿版は2017.11.14に公刊された:https://arxiv.org/abs/1711.04961
そこで、次の研究課題として、如何に進めるべきかを考えている。当面研究課題が無い場合には、課題を探すことになる。しかし今回の場合には、次々と研究課題が存在することが分る。まずは、デカルトの円定理、外接する3つの円が、2つ交わった場合、3つ交わった場合どうなるかの問題が存在する。さらに、今回考えたように、その円の幾つかが、点や直線になった場合にはどうなるかの問題がある。それらの研究内容は今回の論文の6倍から、12倍以上の内容が存在することが予想される。数学の常道である多次元化を考えれば、それらはそれらの研究課題は20倍を超える世界で、挑戦すれば、1冊の著書と生涯の仕事に成り得ると考えられる。そこで如何に進むべきかと思案することになる。論文を出版する事が要求されている場合など、特に他に挑戦する課題が無い場合には、とりあえず、それらの大きな計画の最初の2,3歩を歩み出したいと考えるだろう。より良い課題を持っていれば、その課題に当面挑戦したいと成るだろう。その時の価値判断は 純粋な個人の思いと社会的な影響や共同研究者の意見、希望等が影響するものと考えられる。純粋な個人の価値判断と対社会的な反響に影響されることになる。このとき、その個人の数学観、人生観、価値観などが影響を与え、そのような経緯がその個人の数学を発展させていく原理になる。
今回の場合には、ユークリッド幾何学の世界は、やれば何でもできるので もはや興味も、関心もないという考えが基礎にあるが、全く新奇な現象が出ると分かれば、新規な現象になれるまでは、研究を続行したくなるだろう。人間の心とは極めて微妙で やればできるとなれば、大きな魅力は失われ、予想できない難しい分野に心が向く、真智への愛 が目覚めてくる。創造とは何か、生命とは何か、人工知能の発展とともに絶えず問われることになるだろう。人間にとって真に価値あるものとは何か。人間はどのようなものに感動を覚えるか。絶えず問うていくことになる。
以 上





























0 件のコメント:
コメントを投稿