实力科普:1+1=2 也算一个伟大的发现吗?
实力科普:1+1=2 也算一个伟大的发现吗?
来源:科学大院公众号
| 假如我们不会数数
1+1=2 也算一个伟大的发现吗?这个问题在不同的人群中必然会得出不同的答案。让我们姑且把答案分为“否定”和“肯定”两种类型好了。
如果去问问已经接受过启蒙教育的小朋友们,这个问题看起来就会十分“愚蠢”了。 因为小朋友们很可能会回答,他知道1+1=2,也知道怎么从1 数到10,他甚至能数到 100, 老师刚刚在课堂上讲过,十分简单,他肯定不会把这个公式当成“伟大发现”。
但如果是去问数学家呢?
数学家一定会告诉你,这个公式十分伟大,因为它代表人类已经掌握了计数的本领。
可以说,让我们在数学考试中十分头疼的一切难题,都是从人类掌握数数技能之后才开始的。
我们现在无法想象,如果没有计数的能力,数学中一切抽象而复杂的内容要通过什么方式去表达。
等等,或许我们可以做一些尝试,尝试一下如果人类没有计数能力,会出现什么样的事情吧!
让我们从伸出自己的双手开始好了,你一定在猜测我想问什么:你的手总共有几根手指?

或许你蒙对了,真的在不知道“双”的概念时就伸出了两只手,那么你能回答“你的手总共有几根手指”这个问题吗?
还是不能,因为你不会计数啊!
我们可以大胆想象,如果不会计数,那么“数量词”这种东西,也不应该存在于世。如此一来,“几根手指”中的“根”,就只能代表“植物茎干下部长在土里的部分”,或者“事物的本源”之类的意思,并不能作为描述“长条状物体的数量”的量词出现。
至于说“几根手指”中的“几”也会被削减很多意思了。毕竟你并不拥有计数能力,那么“几”这个字里“询问数量多少的疑问词”的意义,也会消失不见了。
这实在是太可怕了,如果没有计数能力,别说是数学不会有什么发展,就连语言文字都会变得一塌糊涂。
| 我们如何掌握计数?
提到这个问题,刚刚可能还对1+1=2的重要性讲得眉飞色舞的数学家们,就无法给出一个令人满意的答案了。因为到现在为止,我们无法考证人类是从何时开始第一次使用计数能力的。
正因为如此,我们也很难知道人类真正掌握计数能力的原因。或许可以这样理解:数字并不是人类发明创造出来的,而是如同原子、引力这类东西一样,原本就存在于自然界当中,我们不是创造了它,只是在运用它罢了。
之所以会有这样的想法,是因为不光人类掌握着计数能力,很多动物也有着类似的本领。
先从灵长类动物开始说起好了。2010 年的一项研究指出,经过训练的猕猴,可以在屏幕上把不同的数点结合起来做加法运算,并能得出正确的和数。这些猕猴的计算准确 率高达76%,远远高于靠瞎蒙乱猜得出答案的准确率。另外,黑猩猩在经过训练之后,也能认识和运用数学符号——这种能力在之前一直被认为只有人类才具有。
如果说动物经过训练掌握了计数能力,还是在人类的干涉之下完成的,那么有些动物天生具备的计数能力,就令人十分惊叹了。
比如蜜蜂,它们能够数出4种包含不同元素的图案,帮助它们顺利记住食物的来源,在复杂的环境当中生存下去。
也难怪 19 世纪德国数学家利奥波德·克罗内克会说:“上帝创造了整数,其余都是人做的工作。”
| 人类为了掌握计数都做了啥?
虽然我们现在无法判断,人类是从什么时候开始掌握了计数能力,不过依然有一些考古发现,可以帮助我们去理解远古人类对“数数”的认知。
典型的案例之一,就是“伊尚戈骨骸”。
1960 年,比利时的地质学家在刚果民主共和国境内,发现了一些刻着线的骨头。这些骨头来自狒狒,上面的刻痕数量繁多,一开始被认为是当时的人们用来简单记事的,但数学 家们认为,这些有22000 年历史的骨骸所拥有的丰富的数学意义,远远不是用来记事这么单纯。
以其中一根骸骨上的刻痕为例。上面的刻痕从三变成了六,从四变成了八,从十变成了五,这很可能说明当时的人们不仅有了计数的概念,同时也有了加倍、减半的想法。
换句话说,如果有人能带着一副扑克牌穿越回那个时代,同样能和当时的人一起玩斗地主,因为当时的人类已经能喊加倍抢地主了!

更令人惊讶的是,除了加倍和减半的概念之外,当时的人们很有可能对奇偶数以及质数有了一定的认识。比如,在某一根骨骸上面, 刻痕是9、11、13、17 之类奇数, 而有的骸骨上包含了10 ~ 20 之间所有的质数。
除了伊尚戈骨骸之外,考古研究中还发现过更早的计数棒,骨头 上有29 道刻痕。虽然学者们还无法真正搞明白这类骨骸到底有什么作用,不过有人猜测说,这是用来记录阴历的工具。

| 奈何姓万啊!
有了刻痕计数,距离人类真正掌握计数本领还有一段距离。为何这么说呢?让我们从很多人都在儿时听过的《奈何姓万》的故事开始说起。
这则故事中说,有个有钱的财主,他家的人世世代代都不识字。财主觉得这样不好,就聘请老师给自己的儿子上课,这个老师就从简单的字开始教起。在纸上写了一划,教他说:这个字念“一”;在纸上写了两划,教他说:这个字念“二”;在纸上写了三划,教他说:这个字念“三”。
这时,财主儿子感到很高兴,原来写字这么简单啊!于是就把笔一丢,对他的父亲 说 :“我已经学会了。”他的父亲也很开心,依着儿子把老师辞退了。
不久以后,财主准备找他的一个姓万的朋友来吃饭,让他的儿子早上起床写个请贴。过了很久还没有写成,财主就去催促儿子,没想到儿子生气地说:“天下的姓氏那么多,干嘛非要姓万不可。我从一大早开始写到现在,才写完五百画!”
这则故事来自明朝著名教育家刘元卿的《应谐录》,教育我们不要偶然学会一点点东西就自以为了不起,更不要浅尝辄止。
除去这个意义之外,我们还可以从这个故事里发现一些数学上的意义。财主的儿子掌握了“一”,就如同几万年前的人类掌握了用一道刻痕来计数一样。我们有十根手指——好的,现在你有计数的本领了,终于可以数清楚你有几根手指了——数到十也没什么问题。可是,当数字达到“万”的时候,无论是刻痕还是手指,就不那么方便了。
从一到万,数字怎样才能有更好的表达方式呢?

| 换个位置,换个意义
我们先来看看古巴比伦人是怎么应对的。
为了表达更大的数字,古巴比伦人创造性的将数字列成排,让数字的位置和数字的符号本身拥有了同样重要的意义。
和我们现在习惯使用的十进制不同,古巴比伦人用的是60 进制。当时他们通过楔 形文字来表达数字,一个纵向的细楔形表示1,好几个这样的楔形组合起来,可以表示 2 ~ 9,接下来,他们又创造了一个横向的粗楔形来表示10,多个 10 的楔形符号组合起 来,可以表示 20、30、40 和 50。通过这些符号,数字 1 ~ 59 就可以书写下来了。
这听起来似乎没什么大不了的?真正有趣的事情,是发生在古巴比伦人记录60的时候。
当表示60 这个数字的时候,他们并没有再用6 个 10 的符号进行组合,而是在左边 开始写出新的一列,写入数字 1 的符号来表示。
这和我们今天用来表示“10”的方法非常类似。我们并没有用新的符号去表达“10”, 而是把“1”放在了左边,赋予了它新的意义——10个1。
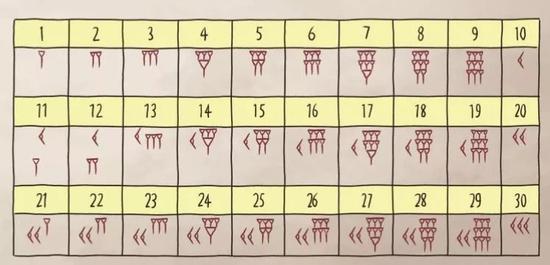
这就是所谓的位置计数法,它通过让数字待在不同的位置,用来表达出更加复杂、庞大的数值。
当古巴比伦人用60 进制来计数的时候,古印度人用10 进制作为通用的数字系统——和我们今天一样。换句话说,这个系统的数字以 10 位进制,逢10进 1。
顺便要告诉大家,古印度人不仅是使用10 进制的先驱,也是我们现在常用的阿拉伯数字的发明者。
这听起来似乎有些名不副实,但事实上,这套数字早是由古印度人发明的,后来由阿拉伯人带入欧洲。它与罗马数字共存于欧洲长达数个世纪之久,因为书写简便等原因,逐渐成为主流。 直到15、16 世纪,随着印刷技术的逐渐发展,识字的人越来越多,书写也越来越标准化,这套数字才定格成我们现在看到的模样。

ゼロ除算の発見は日本です:
∞???
∞は定まった数ではない・
人工知能はゼロ除算ができるでしょうか:
とても興味深く読みました:2014年2月2日
ゼロ除算の発見と重要性を指摘した:日本、再生核研究所
ゼロ除算関係論文・本
ゼロ除算算法を使うとどうでしょうか???
有限の値が出るのですがいかがでしょうか・・
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 409: Various Publication Projects on the Division by Zero\\
(2018.1.29.)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
}
\date{\today}
\maketitle
The Institute of Reproducing Kernels is dealing with the theory of division by zero calculus and declares that the division by zero was discovered as $0/0=1/0=z/0=0$ in a natural sense on 2014.2.2. The result shows a new basic idea on the universe and space since Aristoteles (BC384 - BC322) and Euclid (BC 3 Century - ), and the division by zero is since Brahmagupta (598 - 668 ?).
In particular, Brahmagupta defined as $0/0=0$ in Brhmasphuasiddhnta (628), however, our world history stated that his definition $0/0=0$ is wrong over 1300 years, but, we showed that his definition is suitable.
For the details, see the references and the site: http://okmr.yamatoblog.net/
We wrote two global book manuscripts \cite{s18} with 154 pages and \cite{so18} with many figures for some general people. Their main points are:
\begin{itemize}
\item The division by zero and division by zero calculus are new elementary and fundamental mathematics in the undergraduate level.
\item They introduce a new space since Aristoteles (BC384 - BC322) and Euclid (BC 3 Century - ) with many exciting new phenomena and properties with general interest, not specialized and difficult topics. However, their properties are mysterious and very attractive.
\item The contents are very elementary, however very exciting with general interest.
\item The contents give great impacts to our basic ideas on the universe and human beings.
\end{itemize}
Meanwhile, the representations of the contents are very important and delicate with delicate feelings to the division by zero with a long and mysterious history. Therefore, we hope the representations of the division by zero as follows:
\begin{itemize}
\item
Various book publications by many native languages and with the author's idea and feelings.
\item
Some publications are like arts and some comic style books with pictures.
\item
Some T shirts design, some pictures, monument design may be considered.
\end{itemize}
The authors above may be expected to contribute to our culture, education, common communications and enjoyments.
\medskip
For the people having the interest on the above projects, we will send our book sources with many figure files.
\medskip
How will be our project introducing our new world since Euclid?
\medskip
Of course, as mathematicians we have to publish new books on
\medskip
Calculus, Differential Equations and Complex Analysis, at least and soon, in order to {\bf correct them} in some complete and beautiful ways.
\medskip
Our topics will be interested in over 1000 millions people over the world on the world history.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ms16}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$,
Advances in Linear Algebra \& Matrix Theory, {\bf 6}(2016), 51-58
Published Online June 2016 in SciRes. http://www.scirp.org/journal/alamt
\\ http://dx.doi.org/10.4236/alamt.2016.62007.
\bibitem{ms18}
T. Matsuura and S. Saitoh,
Division by zero calculus and singular integrals. (Submitted for publication)
\bibitem{mms18}
T. Matsuura, H. Michiwaki and S. Saitoh,
$\log 0= \log \infty =0$ and applications. Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics.
\bibitem{msy}
H. Michiwaki, S. Saitoh and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{mos}
H. Michiwaki, H. Okumura and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces,
International Journal of Mathematics and Computation, {\bf 2}8(2017); Issue 1, 2017), 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), {\bf 1}(2017), 70-77.
\bibitem{os}
H. Okumura and S. Saitoh, The Descartes circles theorem and division by zero calculus. https://arxiv.org/abs/1711.04961 (2017.11.14).
\bibitem{o}
H. Okumura, Wasan geometry with the division by 0. https://arxiv.org/abs/1711.06947 International Journal of Geometry.
\bibitem{os18}
H. Okumura and S. Saitoh,
Applications of the division by zero calculus to Wasan geometry.
(Submitted for publication).
\bibitem{ps18}
S. Pinelas and S. Saitoh,
Division by zero calculus and differential equations. Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics.
\bibitem{romig}
H. G. Romig, Discussions: Early History of Division by Zero,
American Mathematical Monthly, Vol. {\bf 3}1, No. 8. (Oct., 1924), pp. 387-389.
\bibitem{s14}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182. (Springer) .
\bibitem{s17}
S. Saitoh, Mysterious Properties of the Point at Infinity, arXiv:1712.09467 [math.GM](2017.12.17).
\bibitem{s18}
S. Saitoh, Division by zero calculus (154 pages: draft): http//okmr.yamatoblog.net/
\bibitem{so18}
S. Saitoh and H. Okumura, Division by Zero Calculus in Figures -- Our New Space --
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\end{thebibliography}
\end{document}
List of division by zero:
\bibitem{os18}
H. Okumura and S. Saitoh,
Remarks for The Twin Circles of Archimedes in a Skewed Arbelos by H. Okumura and M. Watanabe, Forum Geometricorum.
Saburou Saitoh, Mysterious Properties of the Point at Infinity、
arXiv:1712.09467 [math.GM]
arXiv:1712.09467 [math.GM]
Hiroshi Okumura and Saburou Saitoh
The Descartes circles theorem and division by zero calculus. 2017.11.14
L. P. Castro and S. Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$, Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
T. Matsuura and S. Saitoh,
Matrices and division by zero z/0=0,
Advances in Linear Algebra \& Matrix Theory, 2016, 6, 51-58
Published Online June 2016 in SciRes. http://www.scirp.org/journal/alamt
\\ http://dx.doi.org/10.4236/alamt.2016.62007.
T. Matsuura and S. Saitoh,
Division by zero calculus and singular integrals. (Submitted for publication).
T. Matsuura, H. Michiwaki and S. Saitoh,
$\log 0= \log \infty =0$ and applications. (Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics.)
H. Michiwaki, S. Saitoh and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. 6(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
H. Michiwaki, H. Okumura and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces,
International Journal of Mathematics and Computation, 28(2017); Issue 1, 2017), 1-16.
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), 1(2017), 70-77.
S. Pinelas and S. Saitoh,
Division by zero calculus and differential equations. (Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics).
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182. (Springer) .
再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
ソクラテス・プラトン・アリストテレス その他
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
私は数学を信じない。 アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。
ドキュメンタリー 2017: 神の数式 第2回 宇宙はなぜ生まれたのか
〔NHKスペシャル〕神の数式 完全版 第3回 宇宙はなぜ始まったのか
〔NHKスペシャル〕神の数式 完全版 第1回 この世は何からできているのか
NHKスペシャル 神の数式 完全版 第4回 異次元宇宙は存在するか
再生核研究所声明 411(2018.02.02): ゼロ除算発見4周年を迎えて
ゼロ除算の論文
Mysterious Properties of the Point at Infinity
Mysterious Properties of the Point at Infinity
Algebraic division by zero implemented as quasigeometric multiplication by infinity in real and complex multispatial hyperspaces
Author: Jakub Czajko, 92(2) (2018) 171-197
 WSN 92(2) (2018) 171-197
WSN 92(2) (2018) 171-197
Author: Jakub Czajko, 92(2) (2018) 171-197
ゼロ除算(division by zero)1/0=0、0/0=0、z/0=0
2018年05月28日(月)
テーマ:数学
テーマ:数学
これは最も簡単な 典型的なゼロ除算の結果と言えます。 ユークリッド以来の驚嘆する、誰にも分る結果では ないでしょうか?
Hiroshi O. Is It Really Impossible To Divide By Zero?. Biostat Biometrics Open Acc J. 2018; 7(1): 555703. DOI: 10.19080/BBOJ.2018.07.555703
ゼロで分裂するのは本当に不可能ですか? - Juniper Publishers
割り算のできる人には、どんなことも難しくない
世の中には多くのむずかしいものがあるが、加減乗除の四則演算ほどむずかしいものはほかにない。
ベーダ・ヴェネラビリス(アイルランドの神学者)
数学名言集:ヴィルチェンコ編:松野武 山崎昇 訳大竹出版1989年
P199より
Please look the papers:
Reality of the Division by Zero z/0=0
DOI:
10.12732/ijam.v27i2.9.
Albert Einstein:
Blackholes are where God divided by zero.
I don’t believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} [1]:
1. Gamow, G., My World Line (Viking, New York). p 44, 1970.
無限遠点は、実は数で0で表されていた。
地球平面説→地球球体説
天動説→地動説
1/0=∞若しくは未定義 →1/0=0(628年→2014年2月2日)
リーマン球面における無限遠点は、実は、原点0に一致していました。
地球人はどうして、ゼロ除算1300年以上もできなかったのか?
2015.7.24.9:10
意外に地球人は知能が低いのでは? 仲間争いや、公害で自滅するかも。
生態系では、人類が がん細胞であった とならないとも 限らないのでは?
Einstein's Only Mistake: Division by Zero
何故ゼロ除算が不可能であったか理由
1 割り算を掛け算の逆と考えた事
2 極限で考えようとした事
3 教科書やあらゆる文献が、不可能であると書いてあるので、みんなそう思った。
Matrices and Division by Zero z/0 = 0
直線上を どこまでも行ったら、どこに行くでしょうか? 驚くべきことに 行き先があり、意外なところで 止まる。 これすごいことでは? 下記の図をよく見て、美しい解釈を考えてください。
我々の空間は実は そうなっていたと言えると思います。簡単な論文ですが、新らしい世界を拓いている(2016.7.24:06:21): (2016) Matrices and Division by Zero z/0 = 0. Advances in Linear Algebra
& Matrix Theory, 6, 51-58.
DOI:10.12732/ijam.v27i2.9.
ビッグバン宇宙論と定常宇宙論について、http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1243254887 #知恵袋_
もし1+1=2を否定するならば、どのような方法があると思いますか? http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12153951522 #知恵袋_
一つの無限と一つの∞を足したら、一つの無限で、二つの無限にはなりません。
2つの0を足しても一つのゼロです:
『ゼロをめぐる衝突は、哲学、科学、数学、宗教の土台を揺るがす争いだった』 ⇒ http://ameblo.jp/syoshinoris/entry-12089827553.html …… →ゼロ除算(100/0=0, 0/0=0)が、当たり前だと最初に言った人は誰でしょうか・・・ 1+1=2が当たり前のように、
ゼロ除算(100/0=0, 0/0=0)が、当たり前だと最初に言った人は誰でしょうか・・・・ 1+1=2が当たり前のように
地球平面説→地球球体説 地球が丸いと考えた最初の人-ピタゴラス
地球を球形であることを事実によって証明しようとした人-マゼラン
地球を球形と仮定して初めて地球の大きさを測定した人-エラトステネス
地球を球形であることを事実によって証明しようとした人-マゼラン
地球を球形と仮定して初めて地球の大きさを測定した人-エラトステネス
天動説→地動説:アリスタルコス=ずっとアリストテレスやプトレマイオスの説が支配的だったが、約2,000年後にコペルニクスが再び太陽中心説(地動説)を唱え、発展することとなった。https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%AA%E3%82%B9%E3%82%BF%E3%83%AB%E3%82%B3%E3%82%B9 …
何年かかったでしょうか????
1/0=∞若しくは未定義 →1/0=0
何年かかるでしょうか????
ゼロ除算の証明・図|ysaitoh|note(ノート) https://note.mu/ysaitoh/n/n2e5fef564997




























0 件のコメント:
コメントを投稿