(CNN) 地球からはるか120億光年離れたクエーサー(准恒星状天体)に、地球上の海水の100兆倍の水が存在することが、科学者らの研究で明らかになった。
地球の340億倍の質量を持つこのクエーサーを分析していたコロラド大学ボルダー校のジェーソン・グレン准教授らが、数百光年の範囲に広がる大量の水蒸気を発見した。カリフォルニア工科大学がハワイ島マウナケア山に設置している天体望遠鏡で、分光器を使って観測された。
120億光年離れた天体を観測すると、見えるのは120億年前の姿だ。宇宙は136億年前のビッグバンで誕生したと考えられているが、その16億年後にはすでに水が存在していたことになる。
これほどの量の水が見つかったのは観測史上初めて。銀河系内で数光年の範囲に分布する水を全部合わせても、同クエーサーに比べれば4000分の1にすぎないという。
研究には両大学のほか、航空宇宙局(NASA)のジェット推進研究所、カーネギー天文台、ペンシルベニア大学や日本の宇宙科学研究所(ISAS)が参加している。https://www.cnn.co.jp/fringe/30003490.html
とても興味深く読みました:
再生核研究所声明150(2014.3.18) 大宇宙論、宇宙など小さい、小さい、the universe について
(この声明は、最近の特異点解明: 100/0=0, 0/0=0 の研究の進展に伴って 自然に湧いた構想である)
この声明の趣旨は、いわゆる物理学者が考えている宇宙、― 宇宙はビッグバンによって、誕生したという宇宙論を ニュートン力学と同様、幼き断片論と位置づけ、はるかに大きな the universe を志向し、アインシュタインを越えた世界、さらに 古代から続いてきた暗い人類の歴史に 明るい光を灯し、夜明けを迎える時代を切り拓きたいということである。 既に裏付ける思想は 一連の再生核研究所声明で確立していると考える。 ニュ-トン、アインシュタイン、数学の天才たちも、特異点の基本的な性質さえ捉えていなかったことは、明らかである。
簡単な基本、100/0=0,0/0=0 を発見した、精神、魂からすれば、新しい世界史を開拓する思想を語る資格があることの、十分な証拠になると考える。 実際、 - 古来から 続いてきた、人生、世界の難問、人生の意義、生と死の問題、人間社会の在り様の根本問題、基本概念 愛の定義、また、世界の宗教を統一すべく 神の定義さえ きちんと与えている。
The universe について語るとき、最も大事な精神は、神の概念を きちんと理解することである:
そもそも神とは何だろうか、人間とは何だろうか。 動物たちが美しい月をぼんやりと眺めている。 意識はもうろうとしていて、ほんにぼんやりとしか とらえられない。 自らの存在や、ものごとの存在すら明瞭ではない。
人間も、殆ど 同じような存在ではないだろうか。 人類よ、人間の能力など 殆ど動物たちと変わらず、 ぼんやりと世界を眺めているような存在ではないだろうか。 神も、一切の存在も観えず、ただかすかに感じているような存在である。 それゆえに、人間は あらゆる生物たちのレべルに戻って 生物たちから学び、 また原始人に戻って、また子供たちのように 存在すれば 良いと言えるのではないだろうか(再生核研究所声明 122: 神の存在と究極の信仰 - 人間よ 想い煩うことはない。 神は存在して、一切の存在と非存在を しっかりと支えられておられる、 人は必要なときに必要なだけ、 念じるだけで良い; 再生核研究所声明 132 神を如何に感じるか - 神を如何に観るか)。
すなわち、人間よ おごるなかれ、人類の知能など 大したことはなく、内乱や環境汚染で自滅するだろう、と危惧される。
昨年は 数学の存在と物理学が矛盾し、数学とは何かと問うてきた。
数学とは何か ― 数学と人間について
国際数理科学協会会報、No. 81/2012.5, 7―15
No.81, May 2012(pdf 432kb)
に公刊したが、そこで触れた、数学の神秘性については さらにその存念を深め、次のように問うている:
誰が数学を作ったのか? (再生核研究所声明 128: 数学の危機、末期数学について)
時間にもよらず、エネルギーにもよらない世界、それは、宇宙があるとき始まったという考えに 矛盾するものである。 無から世界が創造されたということも 受け入れがたい言明であろう。さらに、the universe には、物理学が未だに近づけない、生命や生命活動、人間の精神活動も歴然として有ることは 否定できない。音楽、芸術に感動している人間の精神は the universe の中に歴然と有るではないか。
ビッグバンで ゼロから、正の量と負の量が生じたとしても、どうしてビッグバンが生じたのか、何が生じせしめたかは 大きな課題として残っている。 数学の多くの等式は 数学を越えて、the universe で論じる場合には、その意味を,解釈をきちんとする必要がある。 The universe には 情報や精神など、まだまだ未知のものが多く存在しているのは当然で、それらが、我々の知らない法則で ものや、エネルギーを動かしているのは 当然である。
そこで、100/0=0,0/0=0 の発見を期に、今やガリレオ・ガリレイの時代、天動説が 地動説に代わる新しい時代に入ったと宣言している。The universe は 知らないことばかりで、満ちている。
以 上
(この声明は、最近の特異点解明: 100/0=0, 0/0=0 の研究の進展に伴って 自然に湧いた構想である)
この声明の趣旨は、いわゆる物理学者が考えている宇宙、― 宇宙はビッグバンによって、誕生したという宇宙論を ニュートン力学と同様、幼き断片論と位置づけ、はるかに大きな the universe を志向し、アインシュタインを越えた世界、さらに 古代から続いてきた暗い人類の歴史に 明るい光を灯し、夜明けを迎える時代を切り拓きたいということである。 既に裏付ける思想は 一連の再生核研究所声明で確立していると考える。 ニュ-トン、アインシュタイン、数学の天才たちも、特異点の基本的な性質さえ捉えていなかったことは、明らかである。
簡単な基本、100/0=0,0/0=0 を発見した、精神、魂からすれば、新しい世界史を開拓する思想を語る資格があることの、十分な証拠になると考える。 実際、 - 古来から 続いてきた、人生、世界の難問、人生の意義、生と死の問題、人間社会の在り様の根本問題、基本概念 愛の定義、また、世界の宗教を統一すべく 神の定義さえ きちんと与えている。
The universe について語るとき、最も大事な精神は、神の概念を きちんと理解することである:
そもそも神とは何だろうか、人間とは何だろうか。 動物たちが美しい月をぼんやりと眺めている。 意識はもうろうとしていて、ほんにぼんやりとしか とらえられない。 自らの存在や、ものごとの存在すら明瞭ではない。
人間も、殆ど 同じような存在ではないだろうか。 人類よ、人間の能力など 殆ど動物たちと変わらず、 ぼんやりと世界を眺めているような存在ではないだろうか。 神も、一切の存在も観えず、ただかすかに感じているような存在である。 それゆえに、人間は あらゆる生物たちのレべルに戻って 生物たちから学び、 また原始人に戻って、また子供たちのように 存在すれば 良いと言えるのではないだろうか(再生核研究所声明 122: 神の存在と究極の信仰 - 人間よ 想い煩うことはない。 神は存在して、一切の存在と非存在を しっかりと支えられておられる、 人は必要なときに必要なだけ、 念じるだけで良い; 再生核研究所声明 132 神を如何に感じるか - 神を如何に観るか)。
すなわち、人間よ おごるなかれ、人類の知能など 大したことはなく、内乱や環境汚染で自滅するだろう、と危惧される。
昨年は 数学の存在と物理学が矛盾し、数学とは何かと問うてきた。
数学とは何か ― 数学と人間について
国際数理科学協会会報、No. 81/2012.5, 7―15
No.81, May 2012(pdf 432kb)
に公刊したが、そこで触れた、数学の神秘性については さらにその存念を深め、次のように問うている:
誰が数学を作ったのか? (再生核研究所声明 128: 数学の危機、末期数学について)
時間にもよらず、エネルギーにもよらない世界、それは、宇宙があるとき始まったという考えに 矛盾するものである。 無から世界が創造されたということも 受け入れがたい言明であろう。さらに、the universe には、物理学が未だに近づけない、生命や生命活動、人間の精神活動も歴然として有ることは 否定できない。音楽、芸術に感動している人間の精神は the universe の中に歴然と有るではないか。
ビッグバンで ゼロから、正の量と負の量が生じたとしても、どうしてビッグバンが生じたのか、何が生じせしめたかは 大きな課題として残っている。 数学の多くの等式は 数学を越えて、the universe で論じる場合には、その意味を,解釈をきちんとする必要がある。 The universe には 情報や精神など、まだまだ未知のものが多く存在しているのは当然で、それらが、我々の知らない法則で ものや、エネルギーを動かしているのは 当然である。
そこで、100/0=0,0/0=0 の発見を期に、今やガリレオ・ガリレイの時代、天動説が 地動説に代わる新しい時代に入ったと宣言している。The universe は 知らないことばかりで、満ちている。
以 上
ゼロの発見には大きく分けると二つの事が在ると言われています。
一つは数学的に、位取りが出来るということ。今一つは、哲学的に無い状態が在るという事実を知ること。http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1462816269
もし1+1=2を否定するならば、どのような方法があると思いますか? http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12153951522 #知恵袋_
一つの無限と一つの∞を足したら、一つの無限で、二つの無限にはなりません。
天動説・・・・・・∞
地動説・・・・・・0
地球平面説→地球球体説
天動説→地動説
何年かかったでしょうか????
1/0=∞若しくは未定義 →1/0=0
何年かかるでしょうか????
割り算のできる人には、どんなことも難しくない
世の中には多くのむずかしいものがあるが、加減乗除の四則演算ほどむずかしいものはほかにない。
ベーダ・ヴェネラビリス
数学名言集:ヴィルチェンコ編:松野武 山崎昇 訳大竹出版1989年
1÷0=0 1÷0=∞・・・・数ではない 1÷0=不定・未定義・・・・狭い考え方をすれば、できない人にはできないが、できる人にはできる。
数学で「A÷0」(ゼロで割る)がダメな理由を教えてください。 http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1411588849 #知恵袋_
割り算を掛け算の逆だと定義した人は、誰でしょう???
multiplication・・・・・増える 掛け算(×) 1より小さい数を掛けたら小さくなる。 大きくなるとは限らない。
0×0=0・・・・・・・・・だから0で割れないと考えた。
唯根拠もなしに、出鱈目に言っている人は世に多い。
ゼロ除算(100/0=0, 0/0=0)が、当たり前だと最初に言った人は誰でしょうか・・・・
1+1=2が当たり前のように
ゼロ除算の証明・図|ysaitoh|note(ノート) https://note.mu/ysaitoh/n/n2e5fef564997
Q)ピラミッドの高さを無限に高くしたら体積はどうなるでしょうか??? A)答えは何と0です。 ゼロ除算の結果です。
ゼロ除算は1+1より優しいです。 何でも0で割れば、0ですから、簡単で美しいです。 1+1=2は 変なのが出てくるので難しいですね。
∞÷0はいくつですか・・・・・・・
∞とはなんですか・・・・・・・・
分からないものは考えられません・・・・・
宇宙消滅説:宇宙が、どんどんドン 拡大を続けると やがて 突然初めの段階 すなわち 0に戻るのではないだろうか。 ゼロ除算は、そのような事を言っているように思われる。 2015年12月3日 10:38
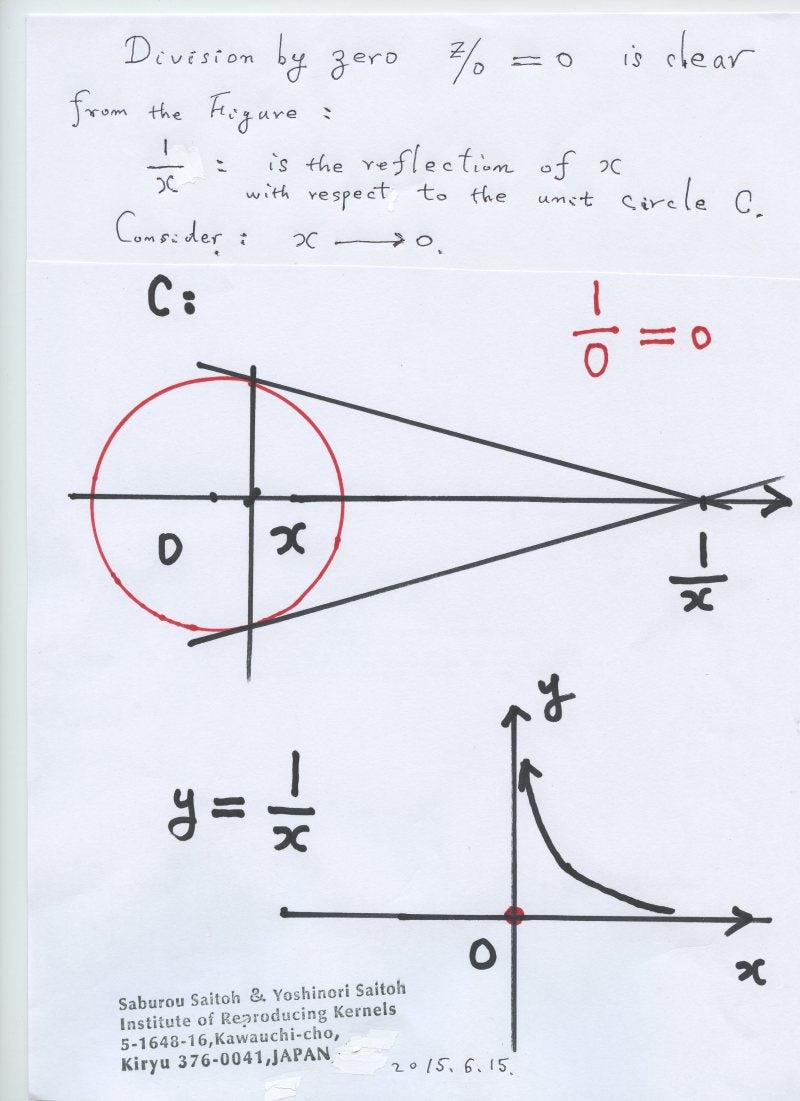
Reality of the Division by Zero z/0 = 0
Mathematics is the alphabet with which God has written the Universe.
数学は神が宇宙を書いたアルファベットだ
Mathematics is the key and door to the sciences.
数学は、科学へとつながる鍵とドアである
This book is written in the mathematical language, and the symbols are triangles, circles and other geometrical figures, without whose help it is impossible to comprehend a single word of it; without which one wanders in vain through a dark labyrinth.
宇宙は数学という言語で書かれている。そしてその文字は三角形であり、円であり、その他の幾何学図形である。これがなかったら、宇宙の言葉は人間にはひとことも理解できない。これがなかったら、人は暗い迷路をたださまようばかりである
ガリレオ・ガリレイさんの名言・格言・英語 一覧リスト
再生核研究所声明 116(2013.5.1): 宇宙空間、星間交流から人間を考える
(1200光年先にようやく生物の存在可能な天体が3つ見つかったという。孤独な地球。かけがいの地球。そこで、何とか地球外生物と交信したいものである。どうしたら、できるだろうか。2013.4.20.16:20 その方法に気づく。慎重に検討して、いずれ提案したい。)
まず、広い宇宙空間において、地球だけが例外で、生物や人間のような知的な生物が存在すると考えるのは 無理があるのではないだろうか。広い宇宙には 人間を越えた知的な生物が存在すると考える。そう感じる。
しかしながら、現代物理学の定説によれば、光より 電波より、早く伝達する手段は無いから、地球上の生物が 人間存在の原理に基づいて(再生核研究所声明 32 : 夜明け ― ノアの方舟)、宇宙空間に進出し、人間の存在領域を拡大しようとしても 広大な宇宙からみれば、それは限られ、地球外生物との直接的な交信、交流は当分、厳しい状況にあると言える。
そこで、発想を逆転させ、宇宙空間交流を意図するには、宇宙空間全体を この地球上に実現すればよいということになる。すなわち あらゆる生命の原理を究明し、一般原理、普遍原理によって、あらゆる可能性を究明して、対応することが出来ると考える。
地球は 宇宙の小さな部分であるが、しかしながら、地球は宇宙全体を 人間の知的な活動によって 包み込むことができると考える。これは一つも矛盾ではなく、部分が全体に等価であるは、数学の世界でも 無限な世界や、解析関数の概念にも存在する。― すなわち、 解析関数の全体の情報は、解析的な どんな点の小さな部分にも、反映されていて、そこから、全体の情報を取り出すことも出来る と なっている。また、エルゴート性の概念も同じような思想になっていると考えられる。
そもそも、対話、交流、愛とは何か と問えば、世界とは、自己の世界に映ったすべて であるとも言い得る。さらに、個々の人間の話題、知識、認識は 狭く限られ、実際多くの考えられるすべての対話は、この地球上に生存する、生物、何十億の人間との対話で、十分可能であると考えられる。さらに、論理的な思考を働かせれば、普遍的な原理によって 人間のあらゆる対話に対する反響は、宇宙空間に問うまでもなく、十分な反響を得ることが出来るだろう。そもそも対話とは、自問自答であるとも言える。実際、自己の内部も 広大な宇宙と同じように無限に広がり、それは全宇宙さえも包み込む存在であるとも考えられる。人間の存在とは、内なる広大な世界と 外なる広大な世界のはざまに存在する、ふらふらした曖昧な 心に代表されるような存在であると言える。
それ故に、この地球上に 生体系を豊かにして、個性を 重んじた多様な世界を築くことによって、実際には 宇宙空間における交流の困難性は 克服できると考える。
結論は、あらゆる生命の存在と存在の可能性を明らかにすることによって この地球上に宇宙を取り組むことによって、宇宙空間交流は 実現できると考える。
そのとき、宇宙間交流の手段とは、もはや光でも電波でもなく、時間にも、空間にも、宇宙にも、エネルギーにも無関係な 数学である と言える。数学こそが 生命の客観的な表現であると言える ― (数学とは何か ― 数学と人間について 国際数理科学協会会報、No. 81/2012.5, 7―15  No.81, May 2012(pdf 432kb))。
No.81, May 2012(pdf 432kb))。
以 上
再生核研究所声明255 (2015.11.3) 神は、平均値として関数値を認識する
(2015.10.30.07:40
朝食後 散歩中突然考えが閃いて、懸案の問題が解決した:
どうして、ゼロ除算では、ローラン展開の正則部の値が 極の値になるのか?
そして、一般に関数値とは何か 想いを巡らしていた。
解決は、驚く程 自分の愚かさを示していると呆れる。 解は 神は、平均値として関数値を認識すると纏められる。実際、解析関数の場合、上記孤立特異点での関数値は、正則の時と全く同じく コ-シーの積分表示で表されている。 解析関数ではコ-シーの積分表示で定義すれば、それは平均値になっており、この意味で考えれば、解析関数は孤立特異点でも 関数値は 拡張されることになる ― 原稿には書いてあるが、認識していなかった。
連続関数などでも関数値の定義は そのまま成り立つ。平均値が定義されない場合には、いろいろな意味での平均値を考えれば良いとなる。解析関数の場合の微分値も同じように重み付き平均値の意味で、統一的に定義でき、拡張される。 いわゆるくりこみ理論で無限値(部)を避けて有限値を捉える操作は、この一般的な原理で捉えられるのではないだろうか。2015.10.30.08:25)
上記のようにメモを取ったのであるが、基本的な概念、関数値とは何かと問うたのである。関数値とは、関数の値のことで、数に数を対応させるとき、その対応を与えるのが関数でよく f 等で表され x 座標の点 x をy 座標の点 yに対応させるのが関数 y = f(x) で、放物線を表す2次関数 y=x^2, 直角双曲線を表す分数関数 y=1/x 等が典型的な例である。ここでは 関数の値 f(x) とは何かと問うたものである。結論を端的に表現するために、関数y=1/xの原点x=0における値を問題にしよう。 このグラフを思い出して、多くの人は困惑するだろう。なぜならば、x が正の方からゼロに近づけば 正の無限に発散し、xが負の方からゼロに近づけば負の無限大に発散するからである。最近発見されたゼロ除算、ゼロで割ることは、その関数値をゼロと解釈すれば良いという簡単なことを言っていて、ゼロ除算はそれを定義とすれば、ゼロ除算は 現代数学の中で未知の世界を拓くと述べてきた。しかし、これは誰でも直感するように、値ゼロは、 原点の周りの値の平均値であることを知り、この定義は自然なものであると 発見初期から認識されてきた。ところが、他方、極めて具体的な解析関数 W = e^{1/z} = 1 + 1/z + 1/2!z^2 + 1/3!z^3 +……. の点 z=0 における値がゼロ除算の結果1であるという結果に接して、人は驚嘆したものと考えられる。複素解析学では、無限位数の極、無限遠点の値を取ると考えられてきたからである。しかしながら、上記の考え、平均値で考えれば、値1をとることが 明確に分かる。実際、原点のコーシー積分表示をこの関数に適用すれば、値1が出てくることが簡単に分かる。そもそも、コーシー積分表示とは 関数の積分路上(簡単に点の周りの円周上での、 小さな円の取り方によらずに定まる)で平均値を取っていることに気づけば良い。
そこで、一般に関数値とは、考えている点の周りの平均値で定義するという原理を考える。
解析関数では 平均値が上手く定義できるから、孤立特異点で、逆に平均値で定義して、関数を拡張できる。しかし、解析的に延長されているとは言えないことに注意して置きたい。 連続関数などは 平均値が定義できるので、関数値の概念は 今までの関数値と同じ意味を有する。関数族では 平均値が上手く定義できない場合もあるが、そのような場合には、平均値のいろいろな考え方によって、関数値の意味が異なると考えよう。この先に、各論の問題が派生する。
以 上
Reality of the Division by Zero $z/0=0$
再生核研究所声明 391(2017.11.1): いろいろな数学者、数学者の心
数学者とはどんな人たちだろうか。回想しながら、感じを表現してみたい。まず、一般に思い浮かぶのは いわゆる世情の表現で、優秀で数学の感覚が発達していて、特にいわゆる数学の理解が早く、問題解きが 得意であるなどではないだろうか。学校でそのような優秀性が現れて、どんどん数学が好きになり、数学の研究者にまでになり、その優秀性を世界的にも示したいと考える数学者は 相当いるのではないだろうか。典型的な発想として、世の難問に挑戦して解決、自己承認を求めた偉大な数学者は多いと言える。始めから優秀ゆえその才能を活かして、数学者の道をひたすらに歩んでいる。その心は意外に純粋、単純で、天才ニュートンとライプニッツの微積分の先取性を生涯争った事実、ニュートンの株投資の失敗、ガロアの決闘、数学の王ガウスの非ユークリッド幾何学の発見者 若きボヤイに対するいわば冷たい対応など結構 想い出される。優秀さゆえに弟子たちに対する冷たい対応なども見られる。結構競争意識が強く、それが碁や将棋の趣味にも通じてもいる原因とみられる。
ところで、どうしても数学を志したい気持ちの本質は 何だろうか。上記才能の他、数理論が好きである、意外に社会、人間関係が好きではない、自分の世界を大事にしたいが あるのではないだろうか。また、数学の絶対性、永遠性に対するあこがれは ギリシャ以来の伝統として有るのではないだろうか。この辺は、そうは才能が無くても、数学好き、数学を趣味として研究している者の精神にあるのでは ないだろうか。
市井の数学愛好者、多田健夫氏について書いてきた
フォームの始まり
フォームの終わり
https://blogs.yahoo.co.jp/kbdmm360/66172415.html
が、別にやることが無くて、別に報いを求めることもなく、数学に集中して人生を終えた者がいる。その心を推察すると、いろいろ考えることが好き、社会生活、人間関係はそうは好きでなく、特別な趣味ややりたいことがない、そして大事なことは 人生に何か記念碑を残したい、できれば、 世の承認 ― あれこれをやったということを認められ、残したいということではないだろうか。このような心は 相当な数学者の基本的な心と言えるのではないだろうか。良い定理を発見して残したい、良い論文を書きたい、著書を出版したい等。
数学者、数学の研究といえば、抽象的で専門化が進み、細分化、深く成りすぎて、お互いに理解が困難に陥ってしまい、孤独で、閉じこもりがちになっているのが憂慮される。しっかりとした動機や目標もなく、ただ先人の理論の先を調べ、調査しているような研究が純粋数学のほとんどであると言えるのではないだろうか。ただ盲目的な研究である。現代のように世知辛い評価時代、あるいは競争の激しい時代になると、しっかりとした方向性、創造性に基づいた研究よりも評価され易い、確立した数理論の先を改善した方が手っ取り早いと、改善型の研究がはびこりかねない。
少し、時間が経てば、当時の流行で見るべきものは無かったと、雑情報、雑論文の溢れていた時代と評価されるだろう。
その様な時、数学者の存在は社会からは、変な社会の人たちに見られてしまうのではないだろうか。
数学者については 下記は素直に全貌が表されている:
再生核研究所声明285(2016.02.10) 数学者の性格、素性について
また、数学の細分化などについては次を参照:
再生核研究所声明 128(2013.8.27): 数学の危機、末期数学について
以 上







































































0 件のコメント:
コメントを投稿