Cybertech TelAviv 2018 レポート(2) 脅威との付き合い方を日常で学ぶイスラエルの教育
講演2日目(1月31日)も、午前中は政府や民間企業の要人から様々な視点でのスピーチが続いた
この中で特に印象の深かったのが、イスラエル教育大臣のMr. Naftali Bennett氏の講演であった。

Bennett氏は、大臣であると同時にサイバーセキュリティのビジネスで大きな成功を成し遂げた起業家でもある。彼は、特にスライド等は使わず、非常に穏やかな語り口でイスラエルの教育の特徴を語った。
最初に彼が紹介したのは、約10日前にハイファのモールに車で行った時のとても印象的なセキュリティ・ガードとのやり取りである。通常であればセキュリティ・ガードは、訪問者にIDを提示させたり、車のトランクを開けさせたりするが、彼はたったひとつのごくシンプルな質問をしただけだったという。
What is your favorite song ?
もし、大臣がテロリストであれば、想定外の質問であることとイスラエルで流行っている歌を思い出すために、答えるのに少し間が必要であったろう。一方、普通の市民同士であれば、なんということもなく答えられる質問である。
IDを提示させたり、車のトランクを開けて中を見たり、金属探知機でチェックすれば、1台あたり2、3分は必要となる。しかし、たったひとつの質問と回答で、数秒で彼は必要十分な仕事をした。余計な時間を費やさず、Quality of Lifeとのバランスを実現したこのプロの仕事に大臣は大きな感銘を受けたそうである。そして、これこそがサイバーセキュリティの分野で我々が最も追求しなければならないポイントである、と指摘した。
この「バランス」を実現するためには三つの要素がある、"Talent" "Living with it" "Serendipity"だそうだ。
最も重要なのは、高度なセキュリティを生み出す優れた才能であり、イスラエルにはこのような才能を生み出すためのエコシステムがあると説明した。特に重視しているのは数学の才能で、過去3年間で18,000人に上る優れた数学人材を生み出したという。
次に重要なのが、子供たちに日常の中でチャレンジ経験をさせることである。例えば、16歳の中学生が、12歳の小学生40人を連れて2日間のハイキングに行く、といった活動を頻繁に行うそうである。このような活動を通して、16歳は40名の子供たち一人ひとりに気を配り、チームをまとめるリーダーシップを学び、12歳の子供たちもチームワークとはどんなものかを実践で学ぶ。子供たち自身が、日常生活の中で「挑戦」を経験し、カウンセラーとなる能力を身につけるそうである。
最後に、セレンディピティ(偶然)の重要性である。いくら人材や組織が優れていても、「計画的にイノベーションを生み出す」ことができるわけではない。ただし、イノベーションを生み出す「チャンスを増やす」環境を作り上げることはできる。この環境の例として、ベエル・シェバに作られたCyberParkを挙げることができる。
座学や記憶が中心の日本の教育、官庁の予算を業界団体に出すことで「産官学共同」を狙う日本のエコシステムとは、大きな違いがあることを感じさせられる。イスラエルを訪れたことのない多くの日本人は「危なくないの?」という質問をし、実際に行ったことのある人間は、私も含めて「危ないことはないよ」と答える。しかし、大臣に言わせれば、イスラエルの人々は「脅威とどのように付き合えばよいかを日常生活の中で知っている」からこそ誰も不安な顔をしていないのである。Living with itを子供の頃から実践している、ということであろう。これがセキュリティ分野での彼等の「厚み」の秘密のひとつなのだ。https://wirelesswire.jp/2018/02/63743/
とても興味深く読みました:
再生核研究所声明325(2016.10.14) ゼロ除算の状況について ー 研究・教育活動への参加を求めて
アリストテレス以来、あるいは西暦628年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題 ゼロ除算は、本質的に新しい局面を迎え、数学における初歩的な部分の欠落が明瞭になってきた。ここ70年を越えても教科書や学術書における数学の初歩的な部分の期待される変更は かつて無かった事である。ユークリッドの考えた空間と解析幾何学などで述べられる我々の空間は実は違っていた。いわゆる非ユークリッド空間とも違う空間が現れた。不思議な飛び、ワープ現象が起きている世界である。ゼロと無限の不思議な関係を述べている。これが我々の空間であると考えられる。
そこで、最近の成果を基に現状における学術書、教科書の変更すべき大勢を外観して置きたい。特に、大学学部までの初等数学において、日本人の寄与は皆無であると言えるから、ゼロ除算の教育、研究は日本人が数学の基礎に貢献できる稀なる好機にもなるので、数学者、教育者など関係者の協力、参加をお願いしたい。
先ず、数学の基礎である四則演算において ゼロでは割れない との世の定説を改め、自然に拡張された分数、割り算で、いつでも四則演算は例外なく、可能であるとする。数学はより美しく、完全であった。さらに、数学の奥深い世界を示している。ゼロ除算を含む体の構造、山田体が確立している。その考えは、殆ど当たり前の従来の演算の修正であるが、分数における考え方に新規で重要、面白い、概念がある。その際、小学生から割り算や分数の定義を除算の意味で 繰り返し減法(道脇方式)で定義し、ゼロ除算は自明であるとし 計算機が割り算を行うような算法で 計算方法も指導する。― この方法は割り算の簡明な算法として児童・生徒たちにも歓迎されるだろう。
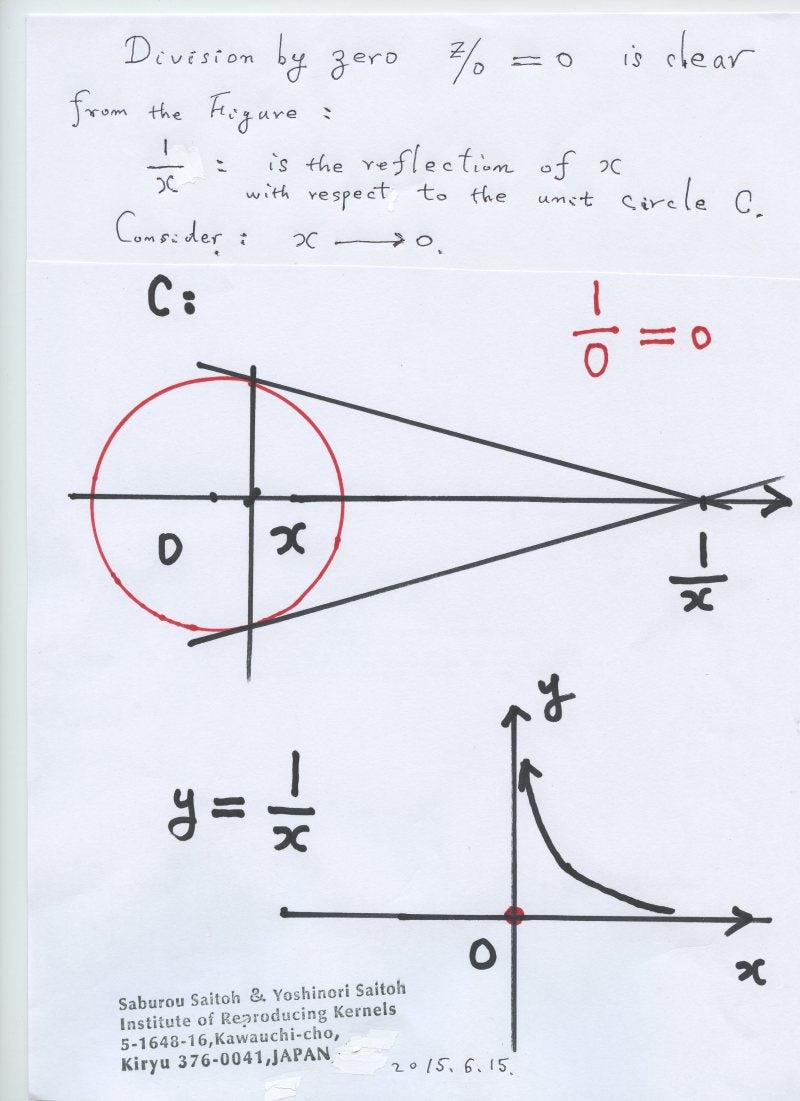
反比例の法則や関数y=1/xの出現の際には、その原点での値はゼロであると 定義する。その広範な応用は 学習過程の進展に従って どんどん触れて行くこととする。応用する。
いわゆるユークリッド幾何学の学習においては、立体射影の概念に早期に触れ、ゼロ除算が拓いた新しい空間像を指導する。無限、無限の彼方の概念、平行線の概念、勾配の概念を変える必要がある。どのように、如何に、カリキュラムに取り組むかは、もちろん、慎重な検討が必要で、数学界、教育界などの関係者による国家的取り組み、協議が必要である。重要項目は、直交座標系で y軸の勾配はゼロであること。真無限における破壊現象、接線などの新しい性質、解析幾何学との美しい関係と調和。すべての直線が原点を代数的に通り、平行な2直線は原点で代数的に交わっていること。行列式と破壊現象の美しい関係など。三角関数や初等関数でも考え方を修正、補充する。直線とは、そもそも、従来の直線に原点を加えたもので、平行線の公理は実は成り立たず、我々の世界は、ユークリッド空間でも、いわゆる非ユークリッド幾何学でもない、新しい空間である。原点は、あらゆる直線の中心になっている。
大学レベルになれば、微積分、線形代数、微分方程式、複素解析をゼロ除算の発展の成果で修正、補充して行く。複素解析学におけるローラン展開の学習以前でも形式的なローラン展開(負べき項を含む展開)の中心の値をゼロ除算で定義し ― ゼロ除算算法、広範な応用を展開する。最も顕著な例は、tan 90度 の値がゼロであることで、いろいろ幾何学的な説明は、我々の空間の認識を変えるのに教育的で楽しい題材である。特に微分係数が正や負の無限大に収束(発散)する時、微分係数をゼロと修正することによって、微分法の多くの公式や定理の表現が簡素化され、教科書の結構な記述の変更が要求される。媒介変数を含む多くの関数族は、ゼロ除算 算法で統一的な視点が与えられる。多くの公式の記述が簡単になり、修正される。新しい、関数の素性が見えてくる。
複素解析学において 無限遠点はゼロで表現されると、コペルニクス的変更(無限とされていたのが実はゼロだった)を行い、極の概念を次のように変更する。極、特異点の定義は そのままであるが、それらの点の近傍で、限りなく無限の値に近づく値を位数まで込めて取るが、特異点自身では、ゼロ除算に言う、有限確定値をとるとする。その有限確定値のいろいろ幾何学的な意味を学ぶ。古典的な鏡像の定説;原点の 原点を中心とする円に関する鏡像は無限遠点であるは、誤りであり、修正し、ゼロであると いろいろな根拠によって説明する。これら、無限遠点の考え方の修正は、ユークリッド以来、我々の空間に対する認識の世界史上における大きな変更であり、数学を越えた世界観の変更を意味している。これはアリストテレスの世界の連続性の概念を変えるもので強力な不連続性を示している。 ― この文脈では天動説が地動説に変わった歴史上の事件が想起される。
ゼロ除算は 物理学を始め、広く自然科学や計算機科学への大きな影響があり、さらに哲学、宗教、文化への大きな影響がある。しかしながら、ゼロ除算の研究成果を教科書、学術書に遅滞なく取り入れていくことは、真智への愛、真理の追究の表現であり、四則演算が自由にできないとなれば、数学者ばかりではなく、人類の名誉にも関わることである。実際、ゼロ除算の歴史は 止むことのない闘争の歴史とともに人類の恥ずべき人類の愚かさの象徴となるだろう。世間ではゼロ除算について不適切な情報が溢れていて 今尚奇怪で抽象的な議論によって混乱していると言える。― 美しい世界が拓けているのに、誰がそれを閉ざそうと、隠したいと、無視したいと考えられるだろうか。我々は間違いを含む、不適切な数学を教えていると言える: ― 再生核研究所声明 41: 世界史、大義、評価、神、最後の審判 ―。
地動説のように真実は、実体は既に明らかである。 ― 研究と研究成果の活用の推進を 大きな夢を懐きながら 要請したい。 研究課題は基礎的で関与する分野は広い、いろいろな方の研究・教育活動への参加を求めたい。素人でも数学の研究に参加できる新しい初歩的な数学を沢山含んでいる。ゼロ除算は発展中の世界史上の事件、問題であると言える。
以 上
追記:
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf DOI:10.12732/ijam.v27i2.9.
*156 Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and
Applications -Plenary Lectures: Isaac 2015, Macau, China.
(Springer Proceedings in Mathematics and Statistics, Vol. 177) Sep. 2016 305 pp. (Springer)
Paper:Division by Zero z/0 = 0 in Euclidean Spaces
Dear Prof. Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
With reference to above, The Editor-in-Chief IJMC (Prof. Haydar Akca) accepted the your paper after getting positive and supporting respond from the reviewer.
Now, we inform you that your paper is accepted for next issue of International Journal of Mathematics and Computation 9 Vol. 28; Issue 1, 2017),
数学基礎学力研究会のホームページ
URLは
再生核研究所声明331(2016.11.04) 提案 ― ゼロ除算の研究は、学部卒論や修士論文の題材に適切
(雨上がり 山間部の散歩で考えが湧いた。ゼロ除算の下記論文は、新しい数学の研究課題で、学部4年生の卒論ゼミの課題、修士論文の研究課題に適切である:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications -Plenary Lectures: Isaac 2015, Macau, China. (Springer Proceedings in Mathematics and Statistics, Vol. 177) Sep. 2016 305 pp. (Springer)
Paper:Division by Zero z/0 = 0 in Euclidean Spaces
Dear Prof. Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
With reference to above, The Editor-in-Chief IJMC (Prof. Haydar Akca) accepted the your paper after getting positive and supporting respond from the reviewer.
Now, we inform you that your paper is accepted for next issue of International Journal of Mathematics and Computation 9 Vol. 28; Issue 1, 2017),
数学基礎学力研究会のホームページ
URLは
簡単に理由を纏めて置きたい。
1) 基礎知識が学部3年生程度で十分で、基本的な結果を議論でき、新しい結果を導ける余地が十分に存在する。新規で、多くの人が興味を持つ課題で国際的にも広く交流できる。
2) 内容は、永い歴史を有する世界史の問題に関わり、空間の考え、勾配、微分、接線、連続性、無限など数学の基礎概念に関与している。相対性理論、ブラックホール、ビッグバン、計算機障害などにも関係している。
3) もともと歴史的な大問題で、ゼロ除算として永い歴史と文化に関わり、広い視点が発展中の生きた数学の中に持てる。
4) 論理には厳格性、精密性、創造性が要求され、数学の精神の涵養に適切である。予断と偏見、思い込みの深さなどについて人間を知ることが出来る。
5) 基礎数学の広範な修正構想に参画でき、物理学など広い研究課題への応用が展望でき、ゼロ除算算法のような新規で基礎数学の新しい手段を身に付けることが出来る。
6) 現在数学は高度化、細分化して、永い学習期間を経て創造的な仕事に取り掛かれるのが普通であるが、ゼロ除算の研究課題では初期段階から、新しい先端の研究に取り掛かれる基礎的な広い研究領域が存在する。ゼロ除算の研究課題は、世にも稀なる夢のある研究課題であると考えられる。― アリストテレス以来、あるいは西暦628年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題 ゼロ除算は、本質的に新しい局面を迎え、数学における初歩的な部分の欠落が明瞭になってきた。ここ70年を越えても教科書や学術書における数学の初歩的な部分の期待される変更は かつて無かった事である。ユークリッドの考えた空間と解析幾何学などで述べられる我々の空間は実は違っていた。いわゆる非ユークリッド空間とも違う空間が現れた。不思議な飛び、ワープ現象が起きている世界である。ゼロと無限の不思議な関係を述べている。これが我々の空間であると考えられる(再生核研究所声明325(2016.10.14) ゼロ除算の状況について ー 研究・教育活動への参加を求めて)。
偉大なる研究は 2段階の発展でなされる という考えによれば、ゼロ除算には何か画期的な発見が大いに期待できるのではないだろうか。 その意味では 天才や超秀才による本格的な研究が期待される。純粋数学として、新しい空間の意義、ワープ現象の解明が、さらには相対性理論との関係、ゼロ除算計算機障害問題の回避など、本質的で重要な問題が存在する。 他方、新しい空間について、ユークリッド幾何学の見直し、世のいろいろな現象におけるゼロ除算の発見など、数学愛好者の趣味の研究にも良いのではないだろうか。 ゼロ除算の研究課題は、理系の多くの人が驚いて楽しめる普遍的な課題で、論文は多くの人に愛される論文と考えられる。
以 上
再生核研究所声明 415(2018.2.19): 数学の進化は単調か、進化と衰退
数学とは ある仮定系を基礎(公理系)に論理的に導かれる関係達の集まりである(No.81, May 2012 (pdf 432kb) www.jams.or.jp/kaiho/kaiho-81.pdf)。数学者はそれゆえに導かれている結果、関係から、新しい関係を導く活動を 研究と称して行っていると言える。分かり易い問題意識は、提起された予想や問題を解決することであるが、それらさえ関係をキチンと確立させることであると表現される。
例えばリーマン予想やフェルマー予想等は歴史的に有名であり、 ピタゴラスの定理やオイラーの公式は基本的で美しい関係式として有名である。数学を進化させる原動力であるが、命題、定理の一般化や精密化なども分かり易い数学の研究姿勢である。 今までの定理を含むような結果は進化した結果であり、知られている関係の詳しい関係の発見も分かり易い数学の進化である。しかしながら、ある分科で一般化、精密化が極端に進めば、理解できる者は限られ、興味関心を抱く者も極端に少なくなり、世の中との関係も薄くなってしまい、 それらの意味は どれほどかと問われる程に成る。 それらの分科から少しずれた人たちは興味も関心も抱かず、 得られたり 論じている世界さえ理解できなくなってしまう。 多くの人は、そのような理論には、興味も関心もないと思ってしまう。そうなれば、数学のそのような状態は衰退した末期的状況と言えるだろう。
その様な数学の姿は 生物の生体のように、誕生の鮮やかさ、成長期のみずみずしさ、衰退期などと同じようにみられる。
人生70年くらいのスパンで見れば、 ある分野の数学の華やかさと衰退そしてほとんど関心がもたれなくなる姿を見ることになる。そのような観点から、永い時代愛されてきた結果は 基本的で衰退することはなく、本質的な結果として時代を超えて存在し、愛されるものになるだろう。それらを表現する言葉は、基本的である、美しい、影響力のある結果であると纏められよう。
数学の質の高い研究として 概念の創造、関係そのものの定義について触れて置こう。微分の概念、積分の概念、勾配の概念、群の概念、位相の概念などなどである。それらの概念の発見は、既に新しい数学の始めであるから、数学の芽のようなもので、基本であればそれだけ価値あるものになる。多くの場合、物理や自然現象からそのような概念が生まれた経緯に注目して置きたい。概念の分かり易い表現は名付けることである。子供が誕生したり、新しい星や島を発見したら命名するようにである。
声明の表題の趣旨は 何事成長の様は単調ではなく、大きな視野を持って研究の状況の判断を行うことの重要性を指摘し、絶えず新しい芽を探し、待つ心のゆとりが大事であることを指摘することである。成果主義の煽りで、成果を急ぎ過ぎて形式的な抹消の研究に囚われ過ぎてしまう危険な世相の時代ではないだろうか。 形式的な評価、数値の量に囚われた実の無い研究の空しい時代の観がしないだろうか。 研究には余裕、楽しみ、本質を求める精神が大事ではないだろうか。 最近 岡潔氏の話題が多いが、岡氏のようには 普通はなれず、そのようには研究者としては生きていけないから、まねることは良くなく、何事ほどほどが大事で、いろいろな在りようも尊重されるべきである。しかしながら、岡氏のよう人物も大事に育てる文化を持つことも 大事ではないだろうか。天才の育成も、平凡な数学者も、数学愛好者の育成もそれぞれに大事ではないだろうか。 高い山は、大きな裾野が広がってこそ有り得る。多様な世界は偉大なる世界であり、人間存在の価値を高める原理である。
ところで、衰退であるが、国家が衰退したり、生物が病的に衰退するように、もともとの発祥の動機、育成のみずみずしさを失い、それらの周辺におかしな在りようが蔓延して 本末転倒なような状況が増大すれば、学問の在り様などもおかしくなって急激に衰退するのではないだろうか。 大学は何をするところかと問うた言葉が想起させられる。何の為の数学か、何のための数学教育かと絶えず自戒して行きたい。疑問を抱いたり、疑ったり、考えたりしてはいけない、と教育の場で指導された生徒の不満の声も結構多い世相はないだろうか。この観点から、
しかしながら、1300年以上に亘って、算術の創始者が0/0は0であると定義していたものを それは間違いであると言ってきた世界の数学界は 相当おかしく、世界の数学界の恥ではないだろうか。
と 繰り返し述べてきた。 数学界のゼロ除算思考停止は 数学界がマインドコントロールされているように現在でも世界の大勢である状況にあると言える。
そこで、我々のゼロ除算についての考えは真実か否か、広く内外の関係者に意見を求めている。関係情報はどんどん公開している。次も参照:
再生核研究所声明 402(2017.11.19): 研究進めるべきか否か - 数学の発展
再生核研究所声明 408(2018.1.25): 数学を越えて ― 価値あるものとは
以 上
再生核研究所声明 416(2018.2.20): ゼロ除算をやってどういう意味が有りますか。何か意味が有りますか。何になるのですか - 回答
ゼロ除算とは例えば、100割るゼロを考えることです。普通に考えると、それは考えられない(不可能)となるのですが、それが分かることが まず第1歩です。この意味が分かるまでは、 次には進めませんので、興味があれば、 次で解説されている最初の方を参照してください:
ゼロ除算の研究状況は、数学基礎学力研究会 サイトで解説が続けられています: http://www.mirun.sctv.jp/~suugaku/
できない(不可能である)と言われれば、何とかできるようにしたくなるのは相当に人間的な素性です。いろいろな冒険者や挑戦者を想い出します。ゼロ除算も子供の頃からできるようにしたいと考えた愛すべき人が結構多く世界にいたり、その問題に人生の大部分を費やして来ている物理学者や計算機科学者たちもいます。現在、ゼロ除算に強い興味を抱いて交流しているのは我々以外でも海外で 大体20名くらいです。ある歴史家の分析によれば、ゼロ除算の物理的な意味を論じ、ゼロ除算は不可能であると最初に述べたのはアリストテレス(BC 384-322) だということです。
また、アインシュタインの人生最大の懸案の問題だったと言われています。実際、物理学には、形式的にゼロ分のが 出て来る公式が沢山有って、分母がゼロの場合が 問題になるからです。いま華やかな宇宙論などでブラックホールや宇宙誕生などと関係があるとされ、ゼロ除算の歴史は 神秘的です。
ところが、ゼロを数学的に厳密に扱い、算術の法則を発見したインドのBrahmagupta (598 -668 ?) は 何と1300年も前に、0/0 はゼロであると定義していたというのです。それ以来1300年を超えてそれは間違いであるとされて来ました。1/0 等は無限大だろうと人は考えて来ました。関数 y=1/x を考えて、 原点の近くで考えれば、限りなく正の無限や負の無限に発散するので人は当然そのように考えるでしょう。天才たちもみんなそうだと考えて、現代に至っています。
ところが偶然4年前に 驚嘆すべき事実を発見しました。 関数 y=1/x の原点の値をゼロとすべきだという結果です。聞いただけで顔色を変える数学者は多く、数年経っても理解できない人は多いのですが、素人がそれは美しい、分かったと喜ぶ人も多いです。算術の創始者Brahmaguptaの考え、結果も 実は 適当であった。正しかったとなります。― 正しいことを間違っているとして来た世界史は 恥ずかしいのではないでしょうか。
この結果、無限の彼方(無限遠点)、無限が 実はゼロ(ゼロで表される)だったとなり、ユークリッド、アリストテレス以来の我々の空間の考えを変える必要が出て来ました。案内の上記サイトで詳しく解説されていますが、私たちの世界観や初等数学全般に大きな影響を与えます。どんどん全く新しい結果、現象が発見されますので、何といっても驚嘆します。 内容レベルが高校生にも十分分かることも驚きです。例えば、y軸の勾配がゼロで、tan (\pi/2) =0 だという驚きの結果です。数学というと人は難しくて分からないだろうと思うのが普通ではないでしょうか。そこで、面白く堪らなく楽しい研究になります。 現在、簡単な図を沢山入れてみんなで見て楽しんで頂けるような本を出版したいと計画を進めています。
内容は上記サイトで、相当素人向きに丁寧に述べているので、興味のある方は解説の最初の方を参考にして下さい。
以 上






































0 件のコメント:
コメントを投稿