「カーリングのストーンはなぜ曲がるのか？」という何百年も続いた謎を研究者らが解明

by Ralf Roletschek

「カーリングのストーンはなぜ曲がるのか？」という問題は、実は何百年にわたって科学的に解き明かされていない謎として存在してきました。そんな中、この謎を数学的に解き明かし、物理的に説明した研究者らが登場しています。

First principles pivot-slide model of the motion of a curling rock: Qualitative and quantitative predictions - ScienceDirect
https://www.sciencedirect.com/science/article/pii/S0165232X17302975

'Eureka': Alberta researcher puts new spin on curling conundrum - Edmonton - CBC News
http://www.cbc.ca/news/canada/edmonton/edmonton-researcher-spin-curling-rock-science-1.4435849

Winter Olympics 2018: Age-Old Curling Question Answered at Last | Inverse
https://www.inverse.com/article/41383-winter-olympics-2018-researchers-answered-curling-question

カナダ・アルバータ大学で熱力学と機械工学を研究するEdward Lozowski博士は「なぜカーリングのストーンは曲がるのか？」ということを、4年間にわたって考え続けた人物。当初は「1年以内には解き明かせるだろう」と考えていたそうですが、カーリングのストーン問題は非常に難しかったとのこと。しかし、2017年のある日、Lozowski博士が朝早くに目覚めると突然、謎を解く数式が頭に浮かんだそうです。そして、すぐに数式を使って計算を行った結果、カーリングのストーンの正しい総旋回時間を導けたといいます。

これまで、「カーリングのストーンはなぜ曲がるのか？」問題は「氷とストーンの間の摩擦の問題」というシンプルな説明しか行われていませんでした。しかし、氷の摩擦ではストーンの軌道が変わる「カール」の大きさを説明できないとLozowski博士は気づきました。そこで、Lozowski博士はノーザン・ブリティッシュ・コロンビア大学の理論物理学者であるMark Shegelski博士と共に、「ストーンが小さな氷の『小石』にくっついた一瞬で回転軸が生じ、それがストーンが曲がるという現象を引き起こしている」ことについて研究を行いました。

カーリングのレーンは「完璧に平ら」にはなっていません。試合前にはアイス・メーカーと呼ばれる製氷技術者がレーンに水をまくため、氷の表面には「小石」のようなものができます。ストーンが放たれたときに音が響くのはこの小石が原因とのこと。

ストーンがこの小石と接触すると、ほんの一瞬だけストーンが小石にくっつき、わずかにストーンの方向が変わります。これは電気丸のこの刃の動きを無理やり止めたことを想像するとわかりやすいのですが、刃の動きを止められた電気丸のこは、今度は機械全体が回りだします。これと同じことがストーンにも起こり、ストーンがすべりながら何千回もこのような方向転換が繰り返されることで、大きなカールが生まれるわけです。

by Benson Kua

これまで行われてきた多くの研究とは違い、Lozowski博士とShegelski氏はストーンが曲がる距離を数式を使って計算しました。2人の数式は、ストーンの半径やストーン下部につけられたリングのきめ細かさ、選手の走り、氷の固さと弾性、ストーンの速度、ストーンがレーンに着地するまでの時間、そして氷の小石のサイズと密度などを考慮したもの。2人の数式は「ぴったりと正しい」というわけではないそうですが、これらの要素の推定の値を数式に当てはめれば、観測しているストーンのカールと近い数字が算出されるといいます。

2人の研究者らの発表によって、カーリングが物理の上に成り立っており、戦略・技巧・体力によって成立する驚異のスポーツであることが示されたわけです。https://gigazine.net/news/20180219-curling-stone-science/

とても興味深く読みました：ゼロ除算の発見は日本　4周年超えました：

再生核研究所声明 415(2018.2.19): 　

数学の進化は単調か、進化と衰退

数学とは　ある仮定系を基礎（公理系）に論理的に導かれる関係達の集まりである（No.81, May 2012　(pdf 432kb)　www.jams.or.jp/kaiho/kaiho-81.pdf）。数学者はそれゆえに導かれている結果、関係から、新しい関係を導く活動を　研究と称して行っていると言える。分かり易い問題意識は、提起された予想や問題を解決することであるが、それらさえ関係をキチンと確立させることであると表現される。

例えばリーマン予想やフェルマー予想等は歴史的に有名であり、　ピタゴラスの定理やオイラーの公式は基本的で美しい関係式として有名である。数学を進化させる原動力であるが、命題、定理の一般化や精密化なども分かり易い数学の研究姿勢である。　今までの定理を含むような結果は進化した結果であり、知られている関係の詳しい関係の発見も分かり易い数学の進化である。しかしながら、ある分科で一般化、精密化が極端に進めば、理解できる者は限られ、興味関心を抱く者も極端に少なくなり、世の中との関係も薄くなってしまい、　それらの意味は　どれほどかと問われる程に成る。　それらの分科から少しずれた人たちは興味も関心も抱かず、　得られたり　論じている世界さえ理解できなくなってしまう。　多くの人は、そのような理論には、興味も関心もないと思ってしまう。そうなれば、数学のそのような状態は衰退した末期的状況と言えるだろう。

その様な数学の姿は　生物の生体のように、誕生の鮮やかさ、成長期のみずみずしさ、衰退期などと同じようにみられる。

人生７０年くらいのスパンで見れば、　ある分野の数学の華やかさと衰退そしてほとんど関心がもたれなくなる姿を見ることになる。そのような観点から、永い時代愛されてきた結果は　基本的で衰退することはなく、本質的な結果として時代を超えて存在し、愛されるものになるだろう。それらを表現する言葉は、基本的である、美しい、影響力のある結果であると纏められよう。

数学の質の高い研究として　概念の創造、関係そのものの定義について触れて置こう。微分の概念、積分の概念、勾配の概念、群の概念、位相の概念などなどである。それらの概念の発見は、既に新しい数学の始めであるから、数学の芽のようなもので、基本であればそれだけ価値あるものになる。多くの場合、物理や自然現象からそのような概念が生まれた経緯に注目して置きたい。概念の分かり易い表現は名付けることである。子供が誕生したり、新しい星や島を発見したら命名するようにである。

声明の表題の趣旨は　何事成長の様は単調ではなく、大きな視野を持って研究の状況の判断を行うことの重要性を指摘し、絶えず新しい芽を探し、待つ心のゆとりが大事であることを指摘することである。成果主義の煽りで、成果を急ぎ過ぎて形式的な抹消の研究に囚われ過ぎてしまう危険な世相の時代ではないだろうか。　形式的な評価、数値の量に囚われた実の無い研究の空しい時代の観がしないだろうか。　研究には余裕、楽しみ、本質を求める精神が大事ではないだろうか。　最近　岡潔氏の話題が多いが、岡氏のようには　普通はなれず、そのようには研究者としては生きていけないから、まねることは良くなく、何事ほどほどが大事で、いろいろな在りようも尊重されるべきである。しかしながら、岡氏のよう人物も大事に育てる文化を持つことも　大事ではないだろうか。天才の育成も、平凡な数学者も、数学愛好者の育成もそれぞれに大事ではないだろうか。　高い山は、大きな裾野が広がってこそ有り得る。多様な世界は偉大なる世界であり、人間存在の価値を高める原理である。

ところで、衰退であるが、国家が衰退したり、生物が病的に衰退するように、もともとの発祥の動機、育成のみずみずしさを失い、それらの周辺におかしな在りようが蔓延して　本末転倒なような状況が増大すれば、学問の在り様などもおかしくなって急激に衰退するのではないだろうか。　大学は何をするところかと問うた言葉が想起させられる。何の為の数学か、何のための数学教育かと絶えず自戒して行きたい。疑問を抱いたり、疑ったり、考えたりしてはいけない、と教育の場で指導された生徒の不満の声も結構多い世相はないだろうか。この観点から、

しかしながら、１３００年以上に亘って、算術の創始者が0/0は0であると定義していたものを　それは間違いであると言ってきた世界の数学界は　相当おかしく、世界の数学界の恥ではないだろうか。

と　繰り返し述べてきた。　数学界のゼロ除算思考停止は　数学界がマインドコントロールされているように現在でも世界の大勢である状況にあると言える。

そこで、我々のゼロ除算についての考えは真実か否か、広く内外の関係者に意見を求めている。関係情報はどんどん公開している。次も参照：

再生核研究所声明 402(2017.11.19): 研究進めるべきか否か　－　数学の発展

再生核研究所声明 408(2018.1.25): 　数学を越えて　―　価値あるものとは

以　上

再生核研究所声明296(2016.05.06)　　　ゼロ除算の混乱

ゼロ除算の研究を進めているが、誠に奇妙な状況と言える。簡潔に焦点を述べておきたい。

ゼロ除算はゼロで割ることを考えることであるが、物理学的にはアリストテレス、ニュートン、アンシュタインの相当に深刻な問題として、問題にされてきた。他方、数学界では６２８年にインドで四則演算の算術の法則の確立、記録とともに永年問題とされてきたが、オイラー、アーベル、リーマン達による、不可能であるという考えと、極限値で考えて無限遠点とする定説が永く定着してきている。

ところが数学界の定説には満足せず、今尚熱い話題、問題として、議論されている。理由は、ゼロで割れないという例外がどうして存在するのかという、素朴な疑問とともに、積極的に、計算機がゼロ除算に出会うと混乱を起こす具体的な懸案問題を解消したいという明確な動機があること、他の動機としてはアインシュタインの相対性理論の上手い解釈を求めることである。これにはアインシュタインが直接言及しているように、ゼロ除算はブラックホールに関係していて、ブラックホールの解明を意図している面もある。偶然、アインシュタイン以後１００年　実に面白い事件が起きていると言える。偶然、２０年以上も考えて解明できたとの著書さえ出版された。―　これは、初めから、間違いであると理由を付けて質問を送っているが、納得させる回答が無い。実名を上げず、具体的に　状況を客観的に述べたい。尚、ゼロ除算はリーマン仮説に密接に関係があるとの情報があるが　詳しいことは分からない。

１：　ゼロ除算回避を目指して、新しい代数的な構造を研究しているグループ、相当な積み重ねのある理論を、体や環の構造で研究している。例えて言うと、ゼロ除算は沢山存在するという、考え方と言える。―　そのような抽象的な理論は不要であると主張している。

２：同じくゼロ除算回避を志向して　何と0/0　を想像上の数として導入し、正、負無限大とともに数として導入して、新しい数の体系と演算の法則を考え、展開している。相当なグループを作っているという。BBCでも報じられたが、数学界の評判は良くないようである。―　そのような抽象的な理論は不要であると主張している。

３：最近、アインシュタインの理論の専門家達が　アインシュタインの理論から、0/0=1, 1/0=無限が出て、ゼロ除算は解決したと報告している。―　しかし、これについては、論理的な間違いがあると具体的に指摘している。結果も我々の結果と違っている。

４：数学界の永い定説では、1/0　は不可能もしくは、極限の考え方で、無限遠点を対応させる. 0/0　は不定、解は何でも良いとなっている。―　数学に基本的な欠落があって、ゼロ除算を導入しなければ数学は不完全であると主張し、新しい世界観を提起している。

ここ２年間の研究で、ゼロ除算は　何時でもゼロz/0=0であるとして、　上記の全ての立場を否定して、新しい理論の建設を進めている。z/0 は　普通の分数ではなく、拡張された意味でと初期から説明しているが、今でも誤解していて、混乱している人は多い、これは真面目に論文を読まず、初めから、問題にしていない証拠であると言える。

上記、関係者たちと交流、討論しているが、中々理解されず、自分たちの建設している理論に固執しているさまがよく現れていて、数学なのに、心情の問題のように感じられる微妙で、奇妙な状況である。

我々のゼロ除算の理論的な簡潔な説明、それを裏付ける具体的な証拠に当たる結果を沢山提示しているが、中々理解されない状況である。

数学界でも永い間の定説で、初めから、問題にしない人は多い状況である。ゼロ除算は算数、ユークリッド幾何学、解析幾何学など、数学の基本に関わることなので、この問題を究明、明確にして頂きたいと要請している：

再生核研究所声明 277(2016.01.26)：アインシュタインの数学不信　―　数学の欠陥

再生核研究所声明 278(2016.01.27)：面白いゼロ除算の混乱と話題

再生核研究所声明279(2016.01.28) ：ゼロ除算の意義

再生核研究所声明280(2016.01.29) : ゼロ除算の公認、認知を求める

我々のゼロ除算について８歳の少女が３週間くらいで、当たり前であると理解し、高校の先生たちも、簡単に理解されている数学、それを数学の専門家や、ゼロ除算の専門家が２年を超えても、誤解したり、受け入れられない状況は誠に奇妙で、アリストテレスの２０００年を超える世の連続性についての固定した世界観や、上記天才数学者たちの足跡、数学界の定説に　まるで全く嵌っている状況に感じられる。

以　上

考えてはいけないことが、考えられるようになった。

説明できないことが説明できることになった。

Matrices and Division by Zero z/0 = 0

http://file.scirp.org/pdf/ALAMT_2016061413593686.pdf

再生核研究所声明316（2016.08.19）　ゼロ除算における誤解

（２０１６年８月１６日夜，風呂で、ゼロ除算の理解の遅れについて　理由を纏める考えが独りでに湧いた。）

６歳の道脇愛羽さんたち親娘が３週間くらいで　ゼロ除算は自明であるとの理解を示したのに、近い人や指導的な数学者たちが１年や２年を経過してもスッキリ理解できない状況は　世にも稀なる事件であると考えられる。ゼロ除算の理解を進めるために　その原因について、掘り下げて纏めて置きたい。

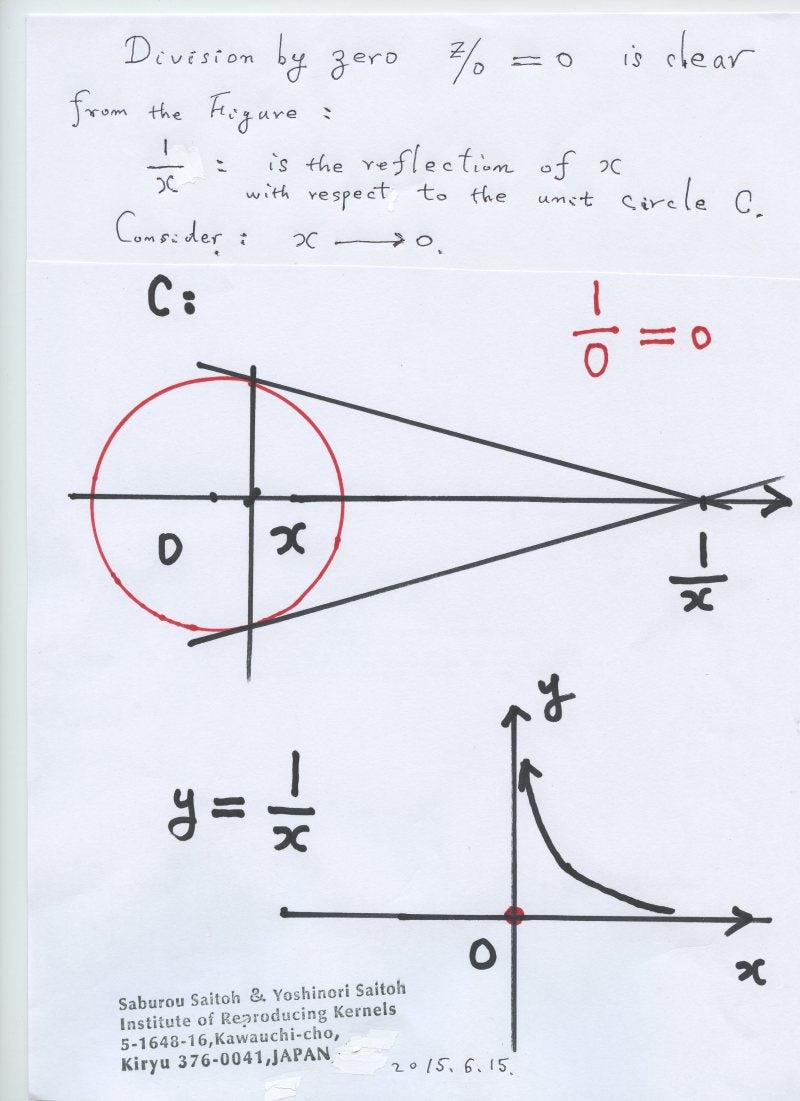
まず、結果を聞いて、とても信じられないと発想する人は極めて多い。割り算の意味を自然に拡張すると1/0=0/0=z/0　となる、関数y=1/xの原点における値がゼロであると結果を表現するのであるが、これらは信じられない、このような結果はダメだと始めから拒否する理由である。

先ずは、ゼロでは割れない、割ったことがない、は全ての人の経験で、ゼロの記録Brahmagupta(598– 668?)　以来の定説である。しかも、ゼロ除算について天才、オイラーの1/0を無限大とする間違いや、不可能性についてはライプニッツ、ハルナックなどの言明があり、厳格な近代数学において確立した定説である。さらに、ゼロ除算についてはアインシュタインが最も深く受け止めていたと言える：（George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} ：Gamow, G., My World Line (Viking, New York). p 44, 1970.）。

一様に思われるのは、割り算は掛け算の逆であり、直ぐに不可能性が証明されてしまうことである。ところが、上記道脇親娘は　割り算と掛け算は別であり、割り算は、等分の考えから、掛け算ではなく、引き算の繰り返し、除算で定義されるという、考えで、このような発想から良き理解に達したと言える。

ゼロで割ったためしがないので、ゼロ除算は興味も、関心もないと言明される人も多い。

また、割り算の（分数の）拡張として得られた。この意味は結構難しく、何と、1/0=0/0=z/0　の正確な意味は分からないというのが　真実である。論文ではこの辺の記述は大事なので、注意して書いているが　真面目に論文を読む者は多いとは言えないないから、とんでもない誤解をして、矛盾だと言ってきている。1/0=0/0=z/0　らが、普通の分数のように掛け算に結びつけると矛盾は直ぐに得られてしまう。したがって、定義された経緯、意味を正確に理解するのが　大事である。数学では、定義をしっかりさせる事は基本である。―　ゼロ除算について、情熱をかけて研究している者で、ゼロ除算の定義をしっかりさせないで混乱している者が多い。

次に関数y=1/xの原点における値がゼロである　は　実は定義であるが、それについて、面白い見解は世に多い。アリストテレス（Aristotelēs、前384年 - 前322年 3月7日）の世界観の強い影響である。ゼロ除算の歴史を詳しく調べている研究者の意見では、ゼロ除算を初めて考えたのはアリストテレスで真空、ゼロの比を考え、それは考えられないとしているという。ゼロ除算の不可能性を述べ、アリストテレスは　真空、ゼロと無限の存在を嫌い、物理的な世界は連続であると考えたという。西欧では　アリストテレスの影響は大きく、聖書にも反映し、ゼロ除算ばかりではなく、ゼロ自身も受け入れるのに１０００年以上もかかったという、歴史解説書がある。ゼロ除算について、始めから国際的に議論しているが、ゼロ除算について異様な様子の背景にはこのようなところにあると考えられる。関数y=1/xの原点における値が無限に行くと考えるのは自然であるが、それがx=0で突然ゼロであるという、強力な不連続性が、感覚的に受け入れられない状況である。解析学における基本概念は　極限の概念であり、連続性の概念である。ゼロ除算は新規な現象であり、なかなか受け入れられない。

ゼロ除算について初期から交流、意見を交わしてきた２０年来の友人との交流から、極めて基本的な誤解がある事が、２年半を越えて判明した。勿論、繰り返して述べてきたことである。ゼロ除算の運用、応用についての注意である。

具体例で注意したい。例えば簡単な関数 y=x/(x -1) において x=1　の値は　形式的にそれを代入して 1/0=0　と考えがちであるが、そのような考えは良くなく、y = 1 + 1/(x -1)　からx=1　の値は1であると考える。関数にゼロ除算を適用するときは注意が必要で、ゼロ除算算法に従う必要があるということである。分子がゼロでなくて、分母がゼロである場合でも意味のある広い世界が現れてきた。現在、ゼロ除算算法は広い分野で意味のある算法を提起しているが、詳しい解説はここでは述べないことにしたい。注意だけを指摘して置きたい。

ゼロ除算は　アリストテレス以来、あるいは西暦６２８年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題　ゼロ除算は、本質的に新しい局面を迎え、数学における基礎的な部分の欠落が明瞭になってきた。ここ７０年を越えても教科書や学術書における数学の基礎的な部分の変更は　かつて無かった事である。と述べ、大きな数学の改革を提案している：

再生核研究所声明312（2016.07.14）　ゼロ除算による　平成の数学改革を提案する

以　上

file:///C:/Users/saito%20saburo/Downloads/P1-Division.pdf

再生核研究所声明 411(2018.02.02): 　ゼロ除算発見4周年を迎えて

ゼロ除算100/0=0を発見して、４周年を迎える。　相当夢中でひたすらに　その真相を求めてきたが、一応の全貌が見渡せ、その基礎と展開、相当先も展望できる状況になった。論文や日本数学会、全体講演者として招待された大きな国際会議などでも発表、著書原案１５４ページも纏め（http://okmr.yamatoblog.net/）基礎はしっかりと確立していると考える。数学の基礎はすっかり当たり前で、具体例は７００件を超え、初等数学全般への影響は思いもよらない程に甚大であると考える：　空間、初等幾何学は　ユークリッド以来の基本的な変更で、無限の彼方や無限が絡む数学は全般的な修正が求められる。何とユークリッドの平行線の公理は成り立たず、すべての直線は原点を通るというが我々の数学、世界であった。y軸の勾配はゼロであり、\tan(\pi/2) =0　である。　初等数学全般の修正が求められている。

数学は、人間を超えたしっかりとした論理で組み立てられており、数学が確立しているのに今でもおかしな議論が世に横行し、世の常識が間違っているにも拘わらず、論文発表や研究がおかしな方向で行われているのは　誠に奇妙な現象であると言える。ゼロ除算から見ると数学は相当おかしく、年々間違った数学やおかしな数学が教育されている現状を思うと、研究者として良心の呵責さえ覚える。

複素解析学では、無限遠点はゼロで表されること、円の中心の鏡像は無限遠点では　なくて中心自身であること、ローラン展開は孤立特異点で意味のある、有限確定値を取ることなど、基本的な間違いが存在する。微分方程式などは欠陥だらけで、誠に恥ずかしい教科書であふれていると言える。　超古典的な高木貞治氏の解析概論にも確かな欠陥が出てきた。勾配や曲率、ローラン展開、コーシーの平均値定理さえ進化できる。

ゼロ除算の歴史は、数学界の避けられない世界史上の汚点に成るばかりか、人類の愚かさの典型的な事実として、世界史上に記録されるだろう。この自覚によって、人類は大きく進化できるのではないだろうか。

そこで、我々は、これらの認知、真相の究明によって、数学界の汚点を解消、世界の文化への貢献を期待したい。

ゼロ除算の真相を明らかにして、基礎数学全般の修正を行い、ここから、人類への教育を進め、世界に貢献することを願っている。

ゼロ除算の発展には　世界史がかかっており、数学界の、社会への対応をも　世界史は見ていると感じられる。　恥の上塗りは世に多いが、数学界がそのような汚点を繰り返さないように願っている。

人の生きるは、真智への愛にある、すなわち、事実を知りたい、本当のことを知りたい、高級に言えば神の意志を知りたいということである。そこで、我々のゼロ除算についての考えは真実か否か、広く内外の関係者に意見を求めている。関係情報はどんどん公開している。

４周年、思えば、世の理解の遅れも反映して、大丈夫か、大丈夫かと自らに問い、ゼロ除算の発展よりも基礎に、基礎にと向かい、基礎固めに集中してきたと言える。それで、著書原案ができたことは、楽しく充実した時代であったと喜びに満ちて回想される。

以　上

List of division by zero:

\bibitem{os18}

H. Okumura and S. Saitoh,

Remarks for The Twin Circles of Archimedes in a Skewed Arbelos by H. Okumura and M. Watanabe, Forum Geometricorum.

Saburou Saitoh, Mysterious Properties of the Point at Infinity、
arXiv:1712.09467 [math.GM]

Hiroshi Okumura and Saburou Saitoh

The Descartes circles theorem and division by zero calculus.　２０１７．１１．１４

https://arxiv.org/abs/1711.04961

L. P. Castro and S. Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.

M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,

New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,　Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.

T. Matsuura and S. Saitoh,

Matrices and division by zero　z/0=0,

Advances in Linear Algebra \& Matrix Theory, 2016, 6, 51-58

Published Online June 2016 in SciRes. http://www.scirp.org/journal/alamt

\\ http://dx.doi.org/10.4236/alamt.2016.62007.

T. Matsuura and S. Saitoh,

Division by zero calculus and singular integrals. (Submitted for publication).

T. Matsuura, H. Michiwaki and S. Saitoh,

$\log 0= \log \infty =0$ and applications. (Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics.)

H. Michiwaki, S. Saitoh and M.Yamada,

Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. 6(2015), 1--8. http://www.ijapm.org/show-63-504-1.html

H. Michiwaki, H. Okumura and S. Saitoh,

Division by Zero $z/0 = 0$ in Euclidean Spaces,

International Journal of Mathematics and Computation, 28(2017); Issue 1, 2017), 1-16.

H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,

Journal of Technology and Social Science (JTSS), 1(2017), 70-77.

S. Pinelas and S. Saitoh,

Division by zero calculus and differential equations. (Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics).

S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/

S. Saitoh, A reproducing kernel theory with some general applications,

Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182. (Springer) .