與現代人日常生活息息相關的數目字,包含阿拉伯世界使用的數字與世界通用的「阿拉伯數字」,是眾所皆知的阿拉伯智慧。
現在阿拉伯世界使用的數字,可溯源至公元七世紀印度數學暨天文學家婆羅摩笈多(Brahmagupta)在628年所作的名為《Brahma原理》(Brāhmasphutasiddhānta)的天文學與數學書籍,書中內容包含九個數字的運用,但是當時印度並未有統一的數字寫法。公元八世紀印度天文學家出使艾巴斯宮廷時,攜帶此書贈予當時艾巴斯的哈里發曼舒爾。曼舒爾哈里發命人翻譯此書,並委任當時的天文學家法撒里(al-Fazārī)參考此書,著作《永恆》(As-Sind Hind)。
九世紀穆斯林科學家花剌子密(al-Khwārizmī or Algoritmi)將此書中的印度數字應用在星曆表上,並於825年著作印度數字十進位制的論文,傳至歐洲。但是歐洲一直到十六世紀才完全使用這套阿拉伯數字。其過程可能是在十一、十二世紀有兩位英國人到安達陸斯學習阿拉伯科學,並將花剌子密的作品翻譯成英文,歐洲人才認識了阿拉伯數字。
穆斯林因為花剌子密的研究而認識數目字。在此之前,阿拉伯人計算時使用字母來代表數字,每一個字母代表一個數字,二十八個阿拉伯字母代表1到10,接著是20、30、40…100,然後是200、300、400…1000。由於當時印度數字有許多型態,阿拉伯人選擇其中一組,並加以調整,成為今日使用於大部分阿拉伯地區,如大敘利亞、伊拉克、阿拉伯海灣國家的數字,阿拉伯人稱之為「印度阿拉伯數字」或「東阿拉伯數字」。
花剌子密根據角度的數目,制定數字的形態。譬如數字1有一個角,2有兩個角,一直到9有九個角。
阿拉伯人在公元873年創造了「0」,不含任何角度。印度人鑑於0會與數目字5(٥)混淆,而於876年以一點(٠)來代表零。今日在大部分阿拉伯地區便使用這套印度數字(١٢٣٤٥٦٧٨٩٠)。而阿拉伯人創造的數字,則由阿拉伯人統治的安達陸斯傳到歐洲,變成世界通用的「阿拉伯數字」,阿拉伯人稱它為「西阿拉伯數字」。https://www.gvm.com.tw/article.html?id=40658
とても興味深く読みました:
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 380: What is the zero?\\
(2017.8.21)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
}
\date{\today}
\maketitle
\section{What is the zero?}
The zero $0$ as the complex number or real number is given clearly by the axions by the complex number field and real number field.
For this fundamental idea, we should consider the {\bf Yamada field} containing the division by zero. The Yamada field and the division by zero calculus will arrange our mathematics, beautifully and completely; this will be our natural and complete mathematics.
\medskip
\section{ Double natures of the zero $z=0$}
The zero point $z=0$ represents the double natures; one is the origin at the starting point and another one is a representation of the point at infinity. One typical and simple example is given by $e^0 = 1,0$, two values. {\bf God loves two}.
\section{Standard value}
\medskip
The zero is a center and stand point (or bases, a standard value) of the coordinates - here we will consider our situation on the complex or real 2 dimensional spaces. By stereographic
projection mapping or the Yamada field, the point at infinity $1/0$ is represented by zero. The origin of the coordinates and the point at infinity correspond each other.
As the standard value, for the point $\omega_n = \exp \left(\frac{\pi}{n}i\right)$ on the unit circle $|z|=1$ on the complex $z$-plane is, for $n = 0$:
\begin{equation}
\omega_0 = \exp \left(\frac{\pi}{0}i\right)=1, \quad \frac{\pi}{0} =0.
\end{equation}
For the mean value
$$
M_n = \frac{x_1 + x_2 +... + x_n}{n},
$$
we have
$$
M_0 = 0 = \frac{0}{0}.
$$
\medskip
\section{ Fruitful world}
\medskip
For example, for very and very general partial differential equations, if the coefficients or terms are zero, then we have some simple differential equations and the extreme case is all the terms are zero; that is, we have trivial equations $0=0$; then its solution is zero. When we consider the converse, we see that the zero world is a fruitful one and it means some vanishing world. Recall Yamane phenomena (\cite{kmsy}), the vanishing result is very simple zero, however, it is the result from some fruitful world. Sometimes, zero means void or nothing world, however, it will show {\bf some changes} as in the Yamane phenomena.
\section{From $0$ to $0$; $0$ means all and all are $0$}
\medskip
As we see from our life figure (\cite{osm}), a story starts from the zero and ends with the zero. This will mean that $0$ means all and all are $0$. The zero is a {\bf mother} or an {\bf origin} of all.
\medskip
\section{ Impossibility}
\medskip
As the solution of the simplest equation
\begin{equation}
ax =b
\end{equation}
we have $x=0$ for $a=0, b\ne 0$ as the standard value, or the Moore-Penrose generalized inverse. This will mean in a sense, the solution does not exist; to solve the equation (6.1) is impossible.
We saw for different parallel lines or different parallel planes, their common points are the origin. Certainly they have the common points of the point at infinity and the point at infinity is represented by zero. However, we can understand also that they have no solutions, no common points, because the point at infinity is an ideal point.
Of course. we can consider the equation (6.1) even the case $a=b=0$ and then we have the solution $x=0$ as we stated.
We will consider the simple differential equation
\begin{equation}
m\frac{d^2x}{dt^2} =0, m\frac{d^2y}{dt^2} =-mg
\end{equation}
with the initial conditions, at $t =0$
\begin{equation}
\frac{dx}{dt} = v_0 \cos \alpha , \frac{d^2x}{dt^2} = \frac{d^2y}{dt^2}=0.
\end{equation}
Then, the highest high $h$, arriving time $t$, the distance $d$ from the starting point at the origin to the point $y(2t) =0$ are given by
\begin{equation}
h = \frac{v_0 \sin^2 \alpha}{2g}, d= \frac{v_0\sin \alpha}{g}
\end{equation}
and
\begin{equation}
t= \frac{v_0 \sin \alpha}{g}.
\end{equation}
For the case $g=0$, we have $h=d =t=0$. We considered the case that they are the infinity; however, our mathematics means zero, which shows impossibility.
These phenomena were looked many cases on the universe; it seems that {\bf God does not like the infinity}.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msy}
H. Michiwaki, S. Saitoh, and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{ms}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$, Advances in Linear Algebra
\& Matrix Theory, 6 (2016), 51-58. http://dx.doi.org/10.4236/alamt.2016.62007 http://www.scirp.org/journal/alamt
\bibitem{mos}
H. Michiwaki, H. Okumura, and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces.
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), 1(2017), 70-77.
\bibitem{romig}
H. G. Romig, Discussions: Early History of Division by Zero,
American Mathematical Monthly, Vol. 31, No. 8. (Oct., 1924), pp. 387-389.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182 (Springer).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\bibitem{ann179}
Announcement 179 (2014.8.30): Division by zero is clear as z/0=0 and it is fundamental in mathematics.
\bibitem{ann185}
Announcement 185 (2014.10.22): The importance of the division by zero $z/0=0$.
\bibitem{ann237}
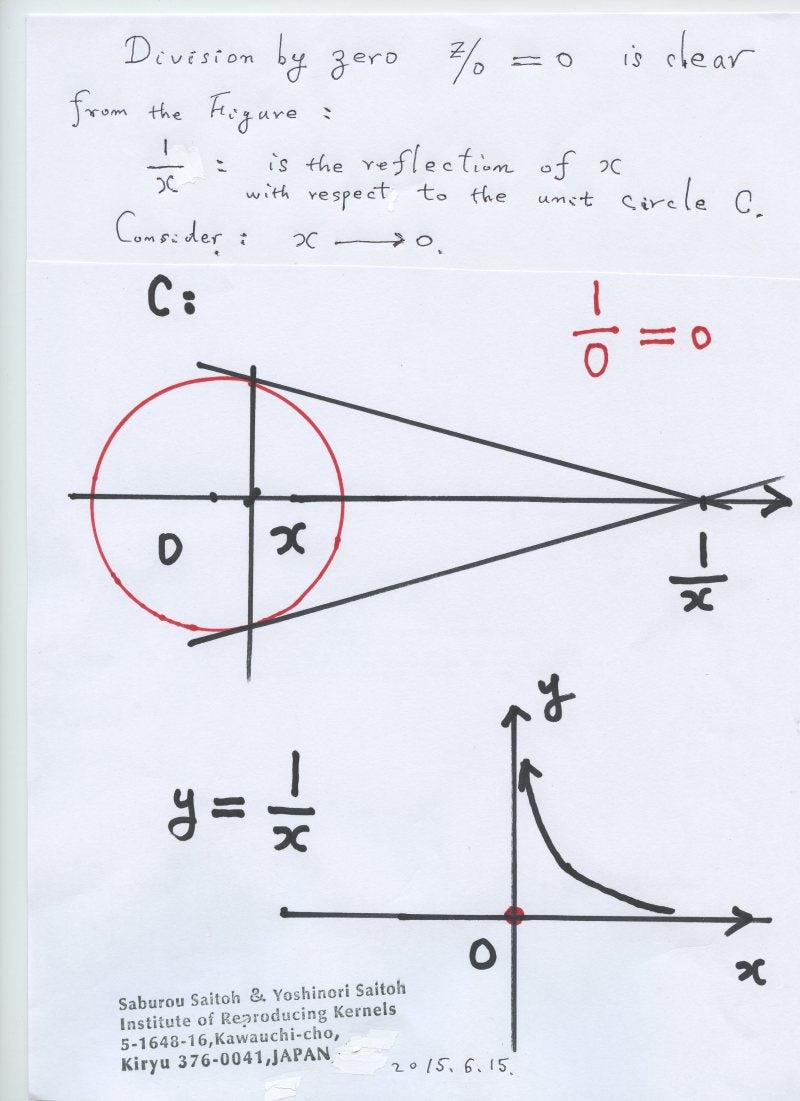
Announcement 237 (2015.6.18): A reality of the division by zero $z/0=0$ by geometrical optics.
\bibitem{ann246}
Announcement 246 (2015.9.17): An interpretation of the division by zero $1/0=0$ by the gradients of lines.
\bibitem{ann247}
Announcement 247 (2015.9.22): The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$.
\bibitem{ann250}
Announcement 250 (2015.10.20): What are numbers? - the Yamada field containing the division by zero $z/0=0$.
\bibitem{ann252}
Announcement 252 (2015.11.1): Circles and
curvature - an interpretation by Mr.
Hiroshi Michiwaki of the division by
zero $r/0 = 0$.
\bibitem{ann281}
Announcement 281 (2016.2.1): The importance of the division by zero $z/0=0$.
\bibitem{ann282}
Announcement 282 (2016.2.2): The Division by Zero $z/0=0$ on the Second Birthday.
\bibitem{ann293}
Announcement 293 (2016.3.27): Parallel lines on the Euclidean plane from the viewpoint of division by zero 1/0=0.
\bibitem{ann300}
Announcement 300 (2016.05.22): New challenges on the division by zero z/0=0.
\bibitem{ann326}
Announcement 326 (2016.10.17): The division by zero z/0=0 - its impact to human beings through education and research.
\bibitem{ann352}
Announcement 352(2017.2.2): On the third birthday of the division by zero z/0=0.
\bibitem{ann354}
Announcement 354(2017.2.8): What are $n = 2,1,0$ regular polygons inscribed in a disc? -- relations of $0$ and infinity.
\bibitem{362}
Announcement 362(2017.5.5): Discovery of the division by zero as
$0/0=1/0=z/0=0$.
\end{thebibliography}
\end{document}
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1
-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi
http://okmr.yamatoblog.net/
Relations of 0 and infinity
Hiroshi Okumura, Saburou Saitoh and Tsutomu Matsuura:
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…
https://sites.google.com/site/sandrapinelas/icddea-2017
2017.8.21.06:37
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
1/0=0、0/0=0、z/0=0
再生核研究所声明 395(2017.11.5): ゼロ除算物語 - 記録、回想
ゼロで割る問題は、ゼロ除算は 2014.2.2 友人二人に100/0=0を認識したとメールしてから、面白いいろいろな経過があって発展している。 再生核研究所声明や解説などで経過を述べてきたが、印象深い事実をできるだけ事実として記録して置きたい。文献は整理して保管するように整理して置きたい。事実を記録するため、以下詳しい記録は特別な仲間以外は この世を去って3年間は未公開としたい。絶えずできるだけ更新、記録を随時追加していきたい。
2017.11.05.05:40 晴天





































































0 件のコメント:
コメントを投稿