相撲(すもう)は、土俵の上で力士が組合って戦う形を取る日本古来の神事や祭りであり、同時に武芸でもあり武道でもある(「弓取り式」の本来の意味から)。古くから祝儀(懸賞金という表現)を得るための興行として、大相撲が行われている。日本由来の武道・格闘技・スポーツとして国際的にも行われている。
概要[編集]
現代の日本においては、スポーツの興行としての大相撲が有名で、相撲は大相撲とほぼ同義に語られることがあるが、元々は日本固有の宗教である神道に基づいた神事であり、日本国内各地で「祭り」として奉納相撲が行われている。そのため、大相撲も他のプロスポーツと比べて礼儀作法などが重視されており、生活様式や風貌なども旧来の風俗が比較的維持されるなど、文化的な側面もある。
日本国内外で同じような形態の格闘技としては、沖縄本島の沖縄角力(シマ)、モンゴルのブフ、中国のシュアイジャオ、朝鮮半島のシルム、トルコのヤールギュレシ、セネガルのラムなどがある。それぞれ独自の名前を持つが、日本国内で紹介される場合には何々相撲(沖縄相撲(琉球角力)、モンゴル相撲、トルコ相撲など)、といった名で呼ばれることが多い。
呼び方[編集]
「すもう」の呼び方は、古代の「スマヰ」から「すまひ」→「すまふ」→「すもう」に訛った。表記としては「角力」、「捔力」(『日本書紀』)、「角觝」(江戸時代において一部で使用)、など。これらの語はもともと「力くらべ」を指す言葉であり、それを「すもう」の漢字表記にあてたものである。19世紀から20世紀初頭までは「すもう」は「角力」と表記されることが多かった[1]。古代には手乞(てごい)とも呼ばれていたと言う説も有る。(手乞とは、相撲の別名とされ、相手の手を掴む事の意、または、素手で勝負をする事を意味する。)
大相撲を取る人は正式名称は「力士」(りきし)といい、また「相撲取り」、親しみを込めて「お相撲さん」とも呼ばれる。
英語では「sumo()」または「sumo-wrestling()」と表記される。
歴史[編集]
「大相撲#歴史」も参照
古代[編集]
日本における相撲の記録の最古は、『古事記』の葦原中国平定の件で、建御雷神(タケミカヅチ)の派遣に対して、出雲の建御名方神(タケミナカタ)が、「然欲爲力競」と言った後タケミカヅチの腕を摑んで投げようとした描写がある。その際タケミカヅチが手を氷柱へ、また氷柱から剣(つるぎ)に変えたため掴めなかった。逆にタケミカヅチはタケミナカタの手を葦のように握り潰してしまい、勝負にならなかったとあり、これが相撲の起源とされている。
人間同士の相撲で最古のものとして、垂仁天皇7年(紀元前23年)7月7日 (旧暦)にある野見宿禰と「當麻蹶速」(当麻蹴速)の「捔力」(「すまいとらしむ・スマヰ」または「すまい・スマヰ」と訓す)での戦いがある(これは柔道の起源ともされている)。この中で「朕聞 當麻蹶速者天下之力士也」「各擧足相蹶則蹶折當麻蹶速之脇骨亦蹈折其腰而殺之」とあり、試合展開は主に蹴り技の応酬であり、最後は宿禰が蹴速の脇骨を蹴り折り、更に倒れた蹴速に踏み付けで加撃して腰骨を踏み折り、絶命させたとされる。これらの記述から、当時の相撲は打撃を主とする格闘技であり、既に勝敗が決した相手にトドメの一撃を加えて命までをも奪った上、しかもそれが賞賛される出来事であった事から見ても、少なくとも現代の相撲とはルールも意識も異なるもので、武芸・武術であったことは明確である[2]。宿禰・蹶速は相撲の始祖として祭られている[3]。
さらに『古事記』の垂仁記には、
ここをもちて軍士の中の力士の軽く捷きを選り聚めて、宣りたまひしく、その御子を取らむ時、すなわちその母王をも掠取れ。髪にもあれ手にもあれ、取り穫む隨に、掬みて控き出すべし。とのりたまひき。ここにその后、かねてかその情を知らしめして、悉にその髪を剃り、髪もちてその頭を覆ひ、また玉の緒を腐して、三重に手に纏かし、また酒もちてその御衣を腐し、全き衣の如服しき。かく設け備へて、その御子を抱きて、城の外にさし出したまひき。ここにもの力士等、その御子を取りて、すなはちその御祖を握りき。ここにその御髪を握れば、御髪自ら落ち、その御手を握れば、玉の緒また絶え、その御衣を握れば、御衣すなはち破れつ。
「相撲節会」を参照
奈良時代から平安時代にかけて、宮中行事の一つとして相撲節会が毎年7月頃に行われるようになる。毎年40人ほどの強者が近衛府により選抜され、宮中で天覧相撲をとった。最初の記録は天平6年(734年)のものであるが[4]、節会を統括する相撲司の初見は養老3年(719年)であることから、8世紀初頭に定着したものと思われる。相撲節会は当初は七夕の宮中行事の余興としての位置づけであったが、後に健児の制が始まると宮中警護人の選抜の意味を持つようになる[5]。時代が下るにしたがって相撲節会は重要な宮中行事となり、先例が積み重なるとともに華やかさを増した。然し同時に、健児の選抜という本来の趣旨は次第に忘れられていった。12世紀に入ると律令制の衰退、都の政情不安定とともに相撲節会は滞るようになり、承安4年(1174年)を最後に廃絶となる[6][7]。
「神事相撲」を参照
中世[編集]
「武家相撲」を参照
相撲節会に求められていた実践的な意味での相撲は、組み打ちの鍛錬として、封建制を成立させた武士の下で広まった。これを武家相撲という。武士の棟梁となった源頼朝は特に相撲を好み、鎌倉を中心に相撲が盛んに行われた[9]。
『日本の礼儀と習慣のスケッチ』より、1867年刊
「土地相撲」を参照
続く足利幕府は、相撲の奨励には消極的であったが、戦国大名は熱心に相撲人の養成に力を注いだ。また、応仁の乱以降都落ちをした貴族とともに京都の相撲文化が地方に伝わり、民衆の間に相撲が定着、相撲を生業とするものが現れる。これを土地相撲、または「草相撲」という。[10]。
近世[編集]
「勧進相撲」を参照
江戸時代に入ると武家相撲はその存在意義を失い、土地相撲が興行化して民衆一般に広がる。興行主はこれを神事相撲の「勧進」にことよせて勧進相撲と称し、また武家相撲も力士を大名の抱えとすることでその名残をとどめた[11]。
近代[編集]
「大相撲」を参照
明治の文明開化で相撲をはじめとする伝統芸能は軒並み危機に陥るが、明治天皇の天覧相撲が繰り返されるなどによりその命脈を保つ。大正14年(1925年)には幕内最高優勝者に授与される天皇賜杯が下賜され、また東京相撲と大阪相撲が合併することにより日本相撲協会が誕生、勧進相撲は大相撲に一本化された。
平成に入って、日本ビーチ相撲連盟というアマチュアの組織が結成された。また、義務教育に武道必修化の必修科目として、相撲・剣道・柔道の三種を基本として加味された。https://ja.wikipedia.org/wiki/%E7%9B%B8%E6%92%B2
とても興味深く読みました:
再生核研究所声明312(2016.07.14) ゼロ除算による 平成の数学改革を提案する
アリストテレス以来、あるいは西暦628年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題 ゼロ除算は、本質的に新しい局面を迎え、数学における基礎的な部分の欠落が明瞭になってきた。ここ70年を越えても教科書や学術書における数学の基礎的な部分の変更は かつて無かった事である。
そこで、最近の成果を基に現状における学術書、教科書の変更すべき大勢を外観して置きたい。特に、大学学部までの初等数学において、日本人の寄与は皆無であると言えるから、日本人が数学の基礎に貢献できる稀なる好機にもなるので、数学者、教育者など関係者の注意を換気したい。― この文脈では稀なる日本人数学者 関孝和の業績が世界の数学に活かせなかったことは 誠に残念に思われる。
先ず、数学の基礎である四則演算において ゼロでは割れない との世の定説を改め、自然に拡張された分数、割り算で、いつでも四則演算は例外なく、可能であるとする。山田体の導入。その際、小学生から割り算や分数の定義を除算の意味で 繰り返し減法(道脇方式)で定義し、ゼロ除算は自明であるとし 計算機が割り算を行うような算法で 計算方法も指導する。― この方法は割り算の簡明な算法として児童に歓迎されるだろう。
反比例の法則や関数y=1/xの出現の際には、その原点での値はゼロであると 定義する。その広範な応用は 学習過程の進展に従って どんどん触れて行くこととする。
いわゆるユークリッド幾何学の学習においては、立体射影の概念に早期に触れ、ゼロ除算が拓いた新しい空間像を指導する。無限、無限の彼方の概念、平行線の概念、勾配の概念を変える必要がある。どのように、如何に、カリキュラムに取り組むかは、もちろん、慎重な検討が必要で、数学界、教育界などの関係者による国家的取り組み、協議が必要である。重要項目は、直角座標系で y軸の勾配はゼロであること。真無限における破壊現象、接線などの新しい性質、解析幾何学との美しい関係と調和。すべての直線が原点を代数的に通り、平行な2直線は原点で代数的に交わっていること。行列式と破壊現象の美しい関係など。
大学レベルになれば、微積分、線形代数、微分方程式、複素解析をゼロ除算の成果で修正、補充して行く。複素解析学におけるローラン展開の学習以前でも形式的なローラン展開(負べき項を含む展開)の中心の値をゼロ除算で定義し、広範な応用を展開する。特に微分係数が正や負の無限大の時、微分係数をゼロと修正することによって、微分法の多くの公式や定理の表現が簡素化され、教科書の結構な記述の変更が要求される。媒介変数を含む多くの関数族は、ゼロ除算 算法で統一的な視点が与えられる。多くの公式の記述が簡単になり、修正される。
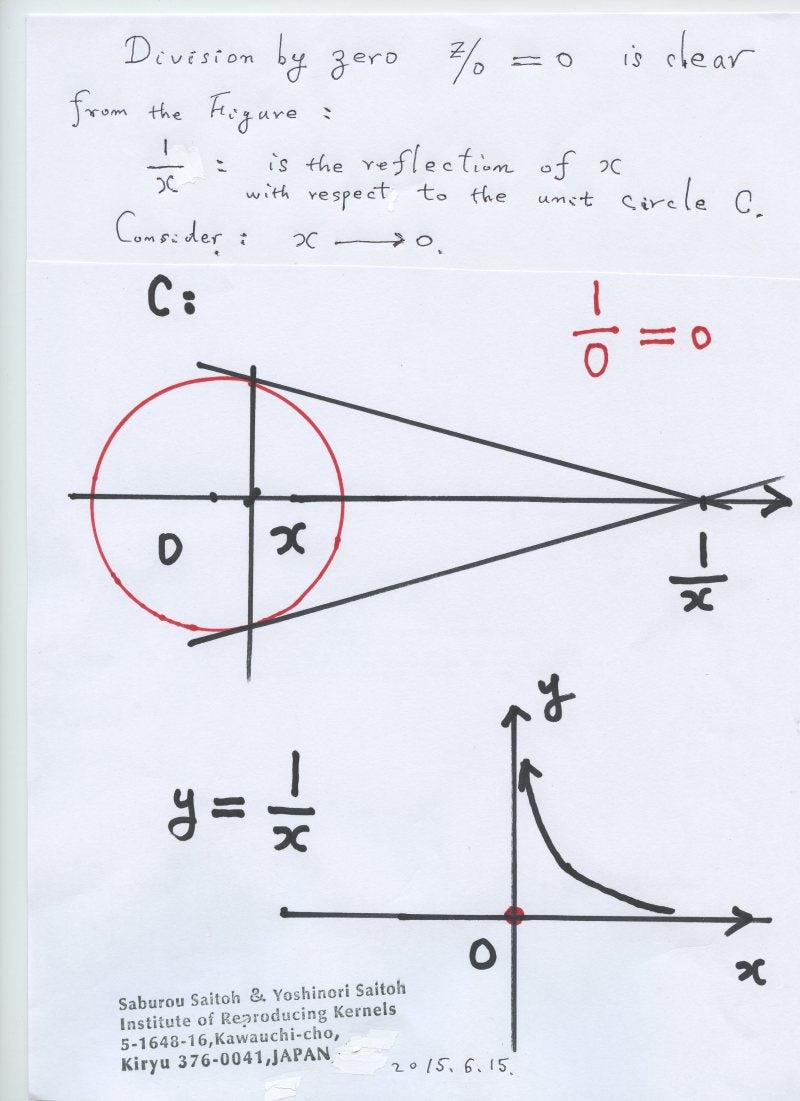
複素解析学においては 無限遠点はゼロで表現されると、コペルニクス的変更(無限とされていたのが実はゼロだった)を行い、極の概念を次のように変更する。極、特異点の定義は そのままであるが、それらの点の近傍で、限りなく無限の値に近づく値を位数まで込めて取るが、特異点では、ゼロ除算に言う、有限確定値をとるとする。その有限確定値のいろいろ幾何学な意味を学ぶ。古典的な鏡像の定説;原点の 原点を中心とする円の鏡像は無限遠点であるは、誤りであり、修正し、ゼロであると いろいろな根拠によって説明する。これら、無限遠点の考えの修正は、ユークリッド以来、我々の空間に対する認識の世界史上に置ける大きな変更であり、数学を越えた世界観の変更を意味している。― この文脈では天動説が地動説に変わった歴史上の事件が想起される。
ゼロ除算は 物理学を始め、広く自然科学や計算機科学への大きな影響が期待される。しかしながら、ゼロ除算の研究成果を教科書、学術書に遅滞なく取り入れていくことは、真智への愛、真理の追究の表現であり、四則演算が自由にできないとなれば、人類の名誉にも関わることである。ゼロ除算の発見は 日本の世界に置ける顕著な貢献として世界史に記録されるだろう。研究と活用の推進を 大きな夢を懐きながら 要請したい。
以 上
追記:
(2016) Matrices and Division by Zero z/0 = 0. Advances in Linear Algebra & Matrix Theory, 6, 51-58.
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdfDOI:10.12732/ijam.v27i2.9.
再生核研究所声明316(2016.08.19) ゼロ除算における誤解
(2016年8月16日夜,風呂で、ゼロ除算の理解の遅れについて 理由を纏める考えが独りでに湧いた。)
6歳の道脇愛羽さんたち親娘が3週間くらいで ゼロ除算は自明であるとの理解を示したのに、近い人や指導的な数学者たちが1年や2年を経過してもスッキリ理解できない状況は 世にも稀なる事件であると考えられる。ゼロ除算の理解を進めるために その原因について、掘り下げて纏めて置きたい。
まず、結果を聞いて、とても信じられないと発想する人は極めて多い。割り算の意味を自然に拡張すると1/0=0/0=z/0 となる、関数y=1/xの原点における値がゼロであると結果を表現するのであるが、これらは信じられない、このような結果はダメだと始めから拒否する理由である。
先ずは、ゼロでは割れない、割ったことがない、は全ての人の経験で、ゼロの記録Brahmagupta(598– 668?) 以来の定説である。しかも、ゼロ除算について天才、オイラーの1/0を無限大とする間違いや、不可能性についてはライプニッツ、ハルナックなどの言明があり、厳格な近代数学において確立した定説である。さらに、ゼロ除算についてはアインシュタインが最も深く受け止めていたと言える:(George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} :Gamow, G., My World Line (Viking, New York). p 44, 1970.)。
一様に思われるのは、割り算は掛け算の逆であり、直ぐに不可能性が証明されてしまうことである。ところが、上記道脇親娘は 割り算と掛け算は別であり、割り算は、等分の考えから、掛け算ではなく、引き算の繰り返し、除算で定義されるという、考えで、このような発想から良き理解に達したと言える。
ゼロで割ったためしがないので、ゼロ除算は興味も、関心もないと言明される人も多い。
また、割り算の(分数の)拡張として得られた。この意味は結構難しく、何と、1/0=0/0=z/0 の正確な意味は分からないというのが 真実である。論文ではこの辺の記述は大事なので、注意して書いているが 真面目に論文を読む者は多いとは言えないないから、とんでもない誤解をして、矛盾だと言ってきている。1/0=0/0=z/0 らが、普通の分数のように掛け算に結びつけると矛盾は直ぐに得られてしまう。したがって、定義された経緯、意味を正確に理解するのが 大事である。数学では、定義をしっかりさせる事は基本である。― ゼロ除算について、情熱をかけて研究している者で、ゼロ除算の定義をしっかりさせないで混乱している者が多い。
次に関数y=1/xの原点における値がゼロである は 実は定義であるが、それについて、面白い見解は世に多い。アリストテレス(Aristotelēs、前384年 - 前322年3月7日)の世界観の強い影響である。ゼロ除算の歴史を詳しく調べている研究者の意見では、ゼロ除算を初めて考えたのはアリストテレスで真空、ゼロの比を考え、それは考えられないとしているという。ゼロ除算の不可能性を述べ、アリストテレスは 真空、ゼロと無限の存在を嫌い、物理的な世界は連続であると考えたという。西欧では アリストテレスの影響は大きく、聖書にも反映し、ゼロ除算ばかりではなく、ゼロ自身も受け入れるのに1000年以上もかかったという、歴史解説書がある。ゼロ除算について、始めから国際的に議論しているが、ゼロ除算について異様な様子の背景にはこのようなところにあると考えられる。関数y=1/xの原点における値が無限に行くと考えるのは自然であるが、それがx=0で突然ゼロであるという、強力な不連続性が、感覚的に受け入れられない状況である。解析学における基本概念は 極限の概念であり、連続性の概念である。ゼロ除算は新規な現象であり、なかなか受け入れられない。
ゼロ除算について初期から交流、意見を交わしてきた20年来の友人との交流から、極めて基本的な誤解がある事が、2年半を越えて判明した。勿論、繰り返して述べてきたことである。ゼロ除算の運用、応用についての注意である。
具体例で注意したい。例えば簡単な関数 y=x/(x -1) において x=1 の値は 形式的にそれを代入して 1/0=0 と考えがちであるが、そのような考えは良くなく、y = 1 + 1/(x -1) からx=1 の値は1であると考える。関数にゼロ除算を適用するときは注意が必要で、ゼロ除算算法に従う必要があるということである。分子がゼロでなくて、分母がゼロである場合でも意味のある広い世界が現れてきた。現在、ゼロ除算算法は広い分野で意味のある算法を提起しているが、詳しい解説はここでは述べないことにしたい。注意だけを指摘して置きたい。
ゼロ除算は アリストテレス以来、あるいは西暦628年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題 ゼロ除算は、本質的に新しい局面を迎え、数学における基礎的な部分の欠落が明瞭になってきた。ここ70年を越えても教科書や学術書における数学の基礎的な部分の変更は かつて無かった事である。と述べ、大きな数学の改革を提案している:
再生核研究所声明312(2016.07.14) ゼロ除算による 平成の数学改革を提案する
以 上






































0 件のコメント:
コメントを投稿