DIVIDING BY ZERO
Diving by zero is perhaps the most puzzling concept in math. How can you divide five cookies among zero people? When dividing 0 by 0, how many zeros are in zero? But why is dividing by zero undefined?
Firstly, lets try to divide by smaller and smaller positive numbers, trying to get as close to zero as possible.
As we divide one by smaller numbers, the quotient increases. One might say that dividing by zero is positive infinity. But what about negatives?
Same result. You could make an equally strong case that dividing by zero is negative infinity.
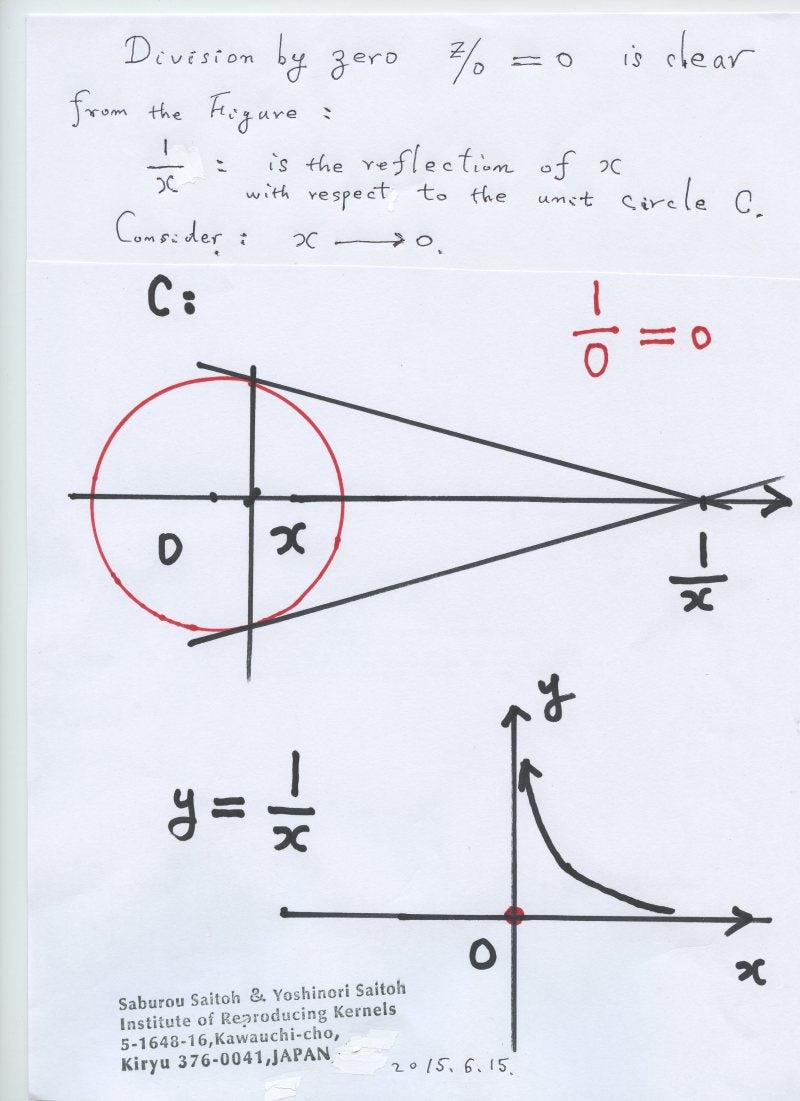
IN CONCLUSION:
There is simply no good answer to dividing by zero. The current understanding of mathematical principals start to break when trying to explain dividing by zero. For now, mathematicians have decided to leave it undefined, as any other answer would be inconsistent with the rest of mathematics today.
とても興味深く読みました:
再生核研究所声明 411(2018.02.02): ゼロ除算発見4周年を迎えて
ゼロ除算100/0=0を発見して、4周年を迎える。 相当夢中でひたすらに その真相を求めてきたが、一応の全貌が見渡せ、その基礎と展開、相当先も展望できる状況になった。論文や日本数学会、全体講演者として招待された大きな国際会議などでも発表、著書原案154ページも纏め(http://okmr.yamatoblog.net/)基礎はしっかりと確立していると考える。数学の基礎はすっかり当たり前で、具体例は700件を超え、初等数学全般への影響は思いもよらない程に甚大であると考える: 空間、初等幾何学は ユークリッド以来の基本的な変更で、無限の彼方や無限が絡む数学は全般的な修正が求められる。何とユークリッドの平行線の公理は成り立たず、すべての直線は原点を通るというが我々の数学、世界であった。y軸の勾配はゼロであり、\tan(\pi/2) =0 である。 初等数学全般の修正が求められている。
数学は、人間を超えたしっかりとした論理で組み立てられており、数学が確立しているのに今でもおかしな議論が世に横行し、世の常識が間違っているにも拘わらず、論文発表や研究がおかしな方向で行われているのは 誠に奇妙な現象であると言える。ゼロ除算から見ると数学は相当おかしく、年々間違った数学やおかしな数学が教育されている現状を思うと、研究者として良心の呵責さえ覚える。
複素解析学では、無限遠点はゼロで表されること、円の中心の鏡像は無限遠点では なくて中心自身であること、ローラン展開は孤立特異点で意味のある、有限確定値を取ることなど、基本的な間違いが存在する。微分方程式などは欠陥だらけで、誠に恥ずかしい教科書であふれていると言える。 超古典的な高木貞治氏の解析概論にも確かな欠陥が出てきた。勾配や曲率、ローラン展開、コーシーの平均値定理さえ進化できる。
ゼロ除算の歴史は、数学界の避けられない世界史上の汚点に成るばかりか、人類の愚かさの典型的な事実として、世界史上に記録されるだろう。この自覚によって、人類は大きく進化できるのではないだろうか。
そこで、我々は、これらの認知、真相の究明によって、数学界の汚点を解消、世界の文化への貢献を期待したい。
ゼロ除算の真相を明らかにして、基礎数学全般の修正を行い、ここから、人類への教育を進め、世界に貢献することを願っている。
ゼロ除算の発展には 世界史がかかっており、数学界の、社会への対応をも 世界史は見ていると感じられる。 恥の上塗りは世に多いが、数学界がそのような汚点を繰り返さないように願っている。
人の生きるは、真智への愛にある、すなわち、事実を知りたい、本当のことを知りたい、高級に言えば神の意志を知りたいということである。そこで、我々のゼロ除算についての考えは真実か否か、広く内外の関係者に意見を求めている。関係情報はどんどん公開している。
4周年、思えば、世の理解の遅れも反映して、大丈夫か、大丈夫かと自らに問い、ゼロ除算の発展よりも基礎に、基礎にと向かい、基礎固めに集中してきたと言える。それで、著書原案ができたことは、楽しく充実した時代であったと喜びに満ちて回想される。
以 上
再生核研究所声明287(2016.02.12) 神秘的なゼロ除算の歴史―数学界で見捨てられていたゼロ除算
(最近 相当 ゼロ除算について幅広く歴史、状況について調べている。)
ゼロ除算とは ゼロで割ることを考えることである。ゼロがインドで628年に記録され、現代数学の四則演算ができていたが、そのとき、既にゼロで割ることか考えられていた。しかしながら、その後1300年を超えてずっと我々の研究成果以外解決には至っていないと言える。実に面白いのは、628年の時に、ゼロ除算は正解と判断される結果1/0=0が期待されていたということである。さらに、詳しく歴史を調べているC.B. Boyer氏の視点では、ゼロ除算を最初に考えたのはアリストテレスであると判断され、アリストテレスは ゼロ除算は不可能であると判断していたという。― 真空で比を考えること、ゼロで割ることはできない。アリストテレスの世界観は 2000年を超えて現代にも及び、我々の得たゼロ除算はアリストテレスの 世界は連続である に反しているので受け入れられないと 複数の数学者が言明されたり、情感でゼロ除算は受け入れられないという人は結構多い。
数学界では,オイラーが積極的に1/0 は無限であるという論文を書き、その誤りを論じた論文がある。アーベルも記号として、それを無限と表し、リーマンもその流れで無限遠点の概念を持ち、リーマン球面を考えている。これらの思想は現代でも踏襲され、超古典アルフォースの複素解析の本にもしっかりと受け継がれている。現代数学の世界の常識である。これらが畏れ多い天才たちの足跡である。こうなると、ゼロ除算は数学的に確定し、何びとと雖も疑うことのない、数学的真実であると考えるのは至極当然である。― ゼロ除算はそのような重い歴史で、数学界では見捨てられていた問題であると言える。
しかしながら、現在に至るも ゼロ除算は広い世界で話題になっている。 まず、顕著な研究者たちの議論を紹介したい:
論理、計算機科学、代数的な体の構造の問題(J. A. Bergstra, Y. Hirshfeld and J. V. Tucker)、
特殊相対性の理論とゼロ除算の関係(J. P. Barukcic and I. Barukcic)、
計算器がゼロ除算に会うと実害が起きることから、ゼロ除算回避の視点から、ゼロ除算の研究(T. S. Reis and James A.D.W. Anderson)。
またフランスでも、奇怪な抽象的な世界を建設している人たちがいるが、個人レベルでもいろいろ奇怪な議論をしている人があとを立たない。また、数学界の難問リーマン予想に関係しているという。
直接議論を行っているところであるが、ゼロ除算で大きな広い話題は 特殊相対性理論、一般相対性理論の関係である。実際、物理とゼロ除算の関係はアリストテレス以来、ニュートン、アインシュタインの中心的な課題で、それはアインシュタインの次の意味深長な言葉で表現される:
Albert Einstein:
Blackholes are where God divided by zero.
I don’t believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} [1]:
1. Gamow, G., My World Line (Viking, New York). p 44, 1970.
数学では不可能である、あるいは無限遠点と確定していた数学、それでも話題が尽きなかったゼロ除算、それが予想外の偶然性から、思いがけない結果、ゼロ除算は一般化された除算,分数の意味で、何時でも唯一つに定まり、解は何時でもゼロであるという、美しい結果が発見された。いろいろ具体的な例を上げて、我々の世界に直接関係する数学で、結果は確定的であるとして、世界の公認を要請している:
再生核研究所声明280(2016.01.29) ゼロ除算の公認、認知を求める
Announcement 282: The Division by Zero $z/0=0$ on the Second Birthday
詳しい解説も次で行っている:
○ 堪らなく楽しい数学-ゼロで割ることを考える(18)
○ 堪らなく楽しい数学-ゼロで割ることを考える(18)
数学基礎学力研究会のホームページ
以 上
何故ゼロ除算が不可能であったか理由
1 割り算を掛け算の逆と考えた事
2 極限で考えようとした事
3 教科書やあらゆる文献が、不可能であると書いてあるので、みんなそう思った。
Matrices and Division by Zero z/0 = 0
再生核研究所声明255 (2015.11.3) 神は、平均値として関数値を認識する
(2015.10.30.07:40
朝食後 散歩中突然考えが閃いて、懸案の問題が解決した:
どうして、ゼロ除算では、ローラン展開の正則部の値が 極の値になるのか?
そして、一般に関数値とは何か 想いを巡らしていた。
解決は、驚く程 自分の愚かさを示していると呆れる。 解は 神は、平均値として関数値を認識すると纏められる。実際、解析関数の場合、上記孤立特異点での関数値は、正則の時と全く同じく コ-シーの積分表示で表されている。 解析関数ではコ-シーの積分表示で定義すれば、それは平均値になっており、この意味で考えれば、解析関数は孤立特異点でも 関数値は 拡張されることになる ― 原稿には書いてあるが、認識していなかった。
連続関数などでも関数値の定義は そのまま成り立つ。平均値が定義されない場合には、いろいろな意味での平均値を考えれば良いとなる。解析関数の場合の微分値も同じように重み付き平均値の意味で、統一的に定義でき、拡張される。 いわゆるくりこみ理論で無限値(部)を避けて有限値を捉える操作は、この一般的な原理で捉えられるのではないだろうか。2015.10.30.08:25)
上記のようにメモを取ったのであるが、基本的な概念、関数値とは何かと問うたのである。関数値とは、関数の値のことで、数に数を対応させるとき、その対応を与えるのが関数でよく f 等で表され x 座標の点 x をy 座標の点 yに対応させるのが関数 y = f(x) で、放物線を表す2次関数 y=x^2, 直角双曲線を表す分数関数 y=1/x 等が典型的な例である。ここでは 関数の値 f(x) とは何かと問うたものである。結論を端的に表現するために、関数y=1/xの原点x=0における値を問題にしよう。 このグラフを思い出して、多くの人は困惑するだろう。なぜならば、x が正の方からゼロに近づけば 正の無限に発散し、xが負の方からゼロに近づけば負の無限大に発散するからである。最近発見されたゼロ除算、ゼロで割ることは、その関数値をゼロと解釈すれば良いという簡単なことを言っていて、ゼロ除算はそれを定義とすれば、ゼロ除算は 現代数学の中で未知の世界を拓くと述べてきた。しかし、これは誰でも直感するように、値ゼロは、 原点の周りの値の平均値であることを知り、この定義は自然なものであると 発見初期から認識されてきた。ところが、他方、極めて具体的な解析関数 W = e^{1/z} = 1 + 1/z + 1/2!z^2 + 1/3!z^3 +……. の点 z=0 における値がゼロ除算の結果1であるという結果に接して、人は驚嘆したものと考えられる。複素解析学では、無限位数の極、無限遠点の値を取ると考えられてきたからである。しかしながら、上記の考え、平均値で考えれば、値1をとることが 明確に分かる。実際、原点のコーシー積分表示をこの関数に適用すれば、値1が出てくることが簡単に分かる。そもそも、コーシー積分表示とは 関数の積分路上(簡単に点の周りの円周上での、 小さな円の取り方によらずに定まる)で平均値を取っていることに気づけば良い。
そこで、一般に関数値とは、考えている点の周りの平均値で定義するという原理を考える。
解析関数では 平均値が上手く定義できるから、孤立特異点で、逆に平均値で定義して、関数を拡張できる。しかし、解析的に延長されているとは言えないことに注意して置きたい。 連続関数などは 平均値が定義できるので、関数値の概念は 今までの関数値と同じ意味を有する。関数族では 平均値が上手く定義できない場合もあるが、そのような場合には、平均値のいろいろな考え方によって、関数値の意味が異なると考えよう。この先に、各論の問題が派生する。
以 上
Reality of the Division by Zero $z/0=0$
再生核研究所声明309(2016.06.28) 真無限と破壊 ― ゼロ除算
3辺の長さをa,b,cとする三角形を考える。その位置で、例えば、1辺bをどんどんのばしていく。一方向でも、双方向でも良い。どこまでも、どこまでも伸ばしていくとどうなるであろうか。bは限りなく長くなるが、結局、辺bは a, cの交点Bと平行な直線になって、 それ以上伸ばすことや長くすることはできないことに気づくだろう。正方向だけに伸びれば、辺cは辺bの方向と平行な半曲線に、負の方向に伸びれば、同様に辺aもBを通るbの方向と平行な半曲線になる。いずれの場合にも、bはそれ以上伸びないと言う意味で真無限の長さと表現できるだろう。もちろん、有限の長さではない。大事な観点は、ある意味で、もはやそれ以上伸びない、大きくならないという意味で、限りがあるとも言える無限である。
途中で作られる三角形の面積は辺cをどんどん伸ばしていくと、どんどん増加し、従来の数学では、面積は無限に発散すると表現してきた。平行線で囲まれる(?)面積、あるいは、平行線で囲まれる(?)部分を切った部分(一方向に辺cを伸ばした場合)は面積無限であると考えるだろう。ところがゼロ除算は、それらの面積はゼロであると述べている。 一般に、長さcをどんどん大きくしていくと、幾らでも大きくなって行くのに対して、真無限に至れば突然ゼロになるという結果がゼロ除算の大事な帰結である。 この現象は関数y=1/x の様子をxが正方向からゼロに近づいた状況を考えれば、理解できるだろう。 1/0=0 である。― c を無限に近づけた状況を知るには、1/c の原点での状況を見れば良い。
実に美しいことには、上記三角形の面積の状況は、3直線で囲まれた部分の面積を3直線を表す方程式で書いて、ゼロ除算の性質を用いると、解析幾何学的にも導かれるという事実である。ゼロ除算の結果を用いると、解析幾何学的に証明されるという事実である。
この事実は普遍的な現象として破壊現象の表現として述べられる。直方体の体積でも、1辺を真無限まで伸ばせば、体積はゼロである。円柱でも真無限まで伸ばせば、体積はゼロである。真無限まで行けば、もともとの形が壊れているためと自然に理解できるだろう。
円や球の場合にも、半径が真無限まで行けば、半平面や半空間になるから、同じように面積や体積がゼロになる。これらは、ゼロ除算と解析幾何学からも導かれ、ゼロ除算は基本的な数学であることが分かる。このことは、空間は、限りなく大きなものではないということをも述べていて、 楽しい。
以 上
再生核研究所声明306(2016.06.21) 平行線公理、非ユークリッド幾何学、そしてゼロ除算
表題について、山間部を散歩している折り新鮮な感覚で、想いが湧いて来た。新しい幾何学の発見で、ボーヤイ・ヤーノシュが父に言われた 平行線の公理を証明できたら、地球の大きさ程のダイヤモンドほどの値打ちがあると言われて、敢然と証明に取り掛かった姿とその帰結である。また、ユークリッドが海岸を散歩しながら幾何学を建設していく情景が鮮やかに想い出された(Liwanovaの『新しい幾何学の発見』(のちに『ロバチェフスキーの世界』と改題)(東京図書刊行)。この件、既に声明に述べているので、まずは確認したい:
再生核研究所声明292(2016.03.25) ユークリッド幾何学、非ユークリッド幾何学、平行線公理、そしてゼロ除算(2016.3.23 朝、目を覚まして、情念と構想が閃いたものである。)
まず基本語をウイキペデアで確認して置こう:
https://ja.wikipedia.org/wiki/%E3%82%A8%E3%82%A6%E3%82%AF%E3%83%AC%E3%82%A4%E3%83%87%E3%82%B9
アレクサンドリアのエウクレイデス(古代ギリシャ語: Εὐκλείδης, Eukleídēs、ラテン語: Euclīdēs、英語: Euclid(ユークリッド)、紀元前3世紀? - )は、古代ギリシアの数学者、天文学者とされる。数学史上最も重要な著作の1つ『原論』(ユークリッド原論)の著者であり、「幾何学の父」と称される。プトレマイオス1世治世下(紀元前323年-283年)のアレクサンドリアで活動した。『原論』は19世紀末から20世紀初頭まで数学(特に幾何学)の教科書として使われ続けた。
https://ja.wikipedia.org/wiki/%E9%9D%9E%E3%83%A6%E3%83%BC%E3%82%AF%E3%83%AA%E3%83%83%E3%83%89%E5%
非ユークリッド幾何学の成立: ニコライ・イワノビッチ・ロバチェフスキーは「幾何学の新原理並びに平行線の完全な理論」(1829年)において、「虚幾何学」と名付けられた幾何学を構成して見せた。これは、鋭角仮定を含む幾何学であった。ボーヤイ・ヤーノシュは父・ボーヤイ・ファルカシュの研究を引き継いで、1832年、「空間論」を出版した。「空間論」では、平行線公準を仮定した幾何学(Σ)、および平行線公準の否定を仮定した幾何学(S)を論じた。更に、1835年「ユークリッド第 11 公準を証明または反駁することの不可能性の証明」において、Σ と S のどちらが現実に成立するかは、如何なる論理的推論によっても決定されないと証明した。
ユークリッド幾何学は 2000年を超えて数学及び論理と あらゆる科学の記述の基礎になってきた。その幾何学を支える平行線の公理については、非ユークリッド幾何学の成立過程で徹底的に検討、議論され、逆に 平行線の公理がユークリッド幾何学の特徴的な仮定(仮説)で証明できない公理であることが明らかにされた。それとともに 数学とは何かに対する認識が根本的に変わり、数学とは公理系(仮説系)の上に建設された理論体系であって、絶対的な真理という概念を失った。
ここで焦点を当てたいのは 平行線の概念である。ユークリッド幾何学における平行線とは 任意の直線に対して、直線上以外の点を通って、それと交わらない直線のことで、平行線がただ1つ存在するというのがユークリッドの公理である。非ユークリッド幾何学では、そのような平行線が全然存在しなかったり、沢山存在する幾何学になっており、そのような幾何学は 実在し、現在も盛んに利用されている。
この平行線の問題が、ゼロ除算の発見1/0=0、台頭によって 驚嘆すべき、形相を帯びてきた。
ユークリッド自身、また、非ユークリッド幾何学の上記発見者たち、それに自ら深い研究をしていた天才ガウスにとっても驚嘆すべき事件であると考えられる。
何と ユークリッド空間で 平行線は ある意味で全て原点で交わっている という、現象が明らかにされた。
もちろん、ここで交わっていることの意味を 従来の意味にとれば、馬鹿馬鹿しいことになる。
そこで、その意味をまず、正確に述べよう。まずは、 イメージから述べる。リーマン球面に立体射影させると 全ユークリッド平面は 球面から北極点を除いた球面上に一対一に写される。そのとき、球面の北極点に対応する点が平面上になく、想像上の点として無限遠点を付け加えて対応させれば、立体射影における円、円対応を考えれば、平面上の平行線は無限遠点で交わっているとして、すっきりと説明され、複素解析学における基本的な世界観を与えている。平行線は無限遠点で 角ゼロ(度)で交わっている(接している)も立体射影における等角性で保証される。あまりの美しさのため、100年を超えて疑われることはなく、世の全ての文献はそのような扱いになっていて数学界の定説である。
ところがゼロ除算1/0=0では 無限遠点は空間の想像上の点として、存在していても、その点、無限遠点は数値では ゼロ(原点)に対応していることが明らかにされた。 すなわち、北極(無限遠点)は南極(原点)と一致している。そのために、平行線は原点で交わっていると解釈できる。もちろん、全ての直線は原点を通っている。
この現象はユークリッド空間の考えを改めるもので、このような性質は解析幾何学、微積分学、複素解析学、物理学など広範に影響を与え、統一的に新しい秩序ある世界を構成していることが明らかにされた。2200年を超えて、ユークリッド幾何学に全く新しい局面が現れたと言える。
平行線の交わりを考えてみる。交わる異なる2直線を1次方程式で書いて、交点の座標を求めて置く。その座標は、平行のとき、分母がゼロになって、交点の座標が求まらないと従来ではなっていたが、ゼロ除算では、それは可能で、原点(0,0)が対応すると解釈できる。ゼロ除算と解析幾何学からの帰結である。上記幾何学的な説明が、ゼロ除算で解析幾何学的にも導かれる。
一般の円の方程式を2次関数で表現すれば、(x^2+y^2) の係数がゼロの場合、直線の一般式になるが、ゼロ除算を用いると、それが保証されるばかりか、直線の中心は 原点である、直線も点円も曲率がゼロであることが導かれる。もちろん、ゼロ除算の世界では、全ての直線は原点を通っている。このとき、原点を無限遠点の映った影ともみなせ、原点はこのような意味で もともとの原点とこの意味での点としての、2重性を有し、この概念は今後大きな意味を有することになるだろう。
ゼロ除算1/0=0は ユークリッド幾何学においても、大きな変革を求めている。
以上
上記で、数学的に大事な観点は、ユークリッド自身そうであったが、平行線公理は真理で、証明されるべきもの、幾何学は絶対的な真理であると非ユークリッド幾何学の出現まで、考えられてきたということである。2000年を超える世界観であった事実である。そこで、平行線の公理を証明しようと多くの人が挑戦してきたが、非ユークリッド幾何学の出現まで不可能であった。実は、証明できない命題であったという全く意外な帰結であった。真に新しい、概念、世界観であった。証明できない命題の存在である。それこそ、世界観を変える、驚嘆すべき世界史上の事件であったと言える。
この事件に関してゼロ除算の発見は、全く異なる世界観を明らかにしている。ユークリッドそして、非ユークリッド幾何学の3人の発見者にとって、全く想像ができなかった、新しい事実である。平行線が 無限の先で交わっているとは ユークリッドは考えなかったと思われるが、近代では、無限の先で交わっていると考えられて来ている。― これには、アーベル、オイラー、リーマンなどの考えが存在する。このような考えは、ここ100年以上、世界の常識、定説になっている。ところがゼロ除算では、無限遠点は 数ではゼロが対応していて、平行線は代数的に原点で交わっている、すべての直線は代数的に原点を通っているという解釈が成り立つことを示している。
ユークリッドの幾何学の建設時の想い、ボーヤイ・ヤーノシュの激しい挑戦の様を、 想い を 深く、いろいろ想像している。
以 上
Matrices and Division by Zero z/0 = 0
表題について、山間部を散歩している折り新鮮な感覚で、想いが湧いて来た。新しい幾何学の発見で、ボーヤイ・ヤーノシュが父に言われた 平行線の公理を証明できたら、地球の大きさ程のダイヤモンドほどの値打ちがあると言われて、敢然と証明に取り掛かった姿とその帰結である。また、ユークリッドが海岸を散歩しながら幾何学を建設していく情景が鮮やかに想い出された(Liwanovaの『新しい幾何学の発見』(のちに『ロバチェフスキーの世界』と改題)(東京図書刊行)。この件、既に声明に述べているので、まずは確認したい:
再生核研究所声明292(2016.03.25) ユークリッド幾何学、非ユークリッド幾何学、平行線公理、そしてゼロ除算(2016.3.23 朝、目を覚まして、情念と構想が閃いたものである。)
まず基本語をウイキペデアで確認して置こう:
https://ja.wikipedia.org/wiki/%E3%82%A8%E3%82%A6%E3%82%AF%E3%83%AC%E3%82%A4%E3%83%87%E3%82%B9
アレクサンドリアのエウクレイデス(古代ギリシャ語: Εὐκλείδης, Eukleídēs、ラテン語: Euclīdēs、英語: Euclid(ユークリッド)、紀元前3世紀? - )は、古代ギリシアの数学者、天文学者とされる。数学史上最も重要な著作の1つ『原論』(ユークリッド原論)の著者であり、「幾何学の父」と称される。プトレマイオス1世治世下(紀元前323年-283年)のアレクサンドリアで活動した。『原論』は19世紀末から20世紀初頭まで数学(特に幾何学)の教科書として使われ続けた。
https://ja.wikipedia.org/wiki/%E9%9D%9E%E3%83%A6%E3%83%BC%E3%82%AF%E3%83%AA%E3%83%83%E3%83%89%E5%
非ユークリッド幾何学の成立: ニコライ・イワノビッチ・ロバチェフスキーは「幾何学の新原理並びに平行線の完全な理論」(1829年)において、「虚幾何学」と名付けられた幾何学を構成して見せた。これは、鋭角仮定を含む幾何学であった。ボーヤイ・ヤーノシュは父・ボーヤイ・ファルカシュの研究を引き継いで、1832年、「空間論」を出版した。「空間論」では、平行線公準を仮定した幾何学(Σ)、および平行線公準の否定を仮定した幾何学(S)を論じた。更に、1835年「ユークリッド第 11 公準を証明または反駁することの不可能性の証明」において、Σ と S のどちらが現実に成立するかは、如何なる論理的推論によっても決定されないと証明した。
ユークリッド幾何学は 2000年を超えて数学及び論理と あらゆる科学の記述の基礎になってきた。その幾何学を支える平行線の公理については、非ユークリッド幾何学の成立過程で徹底的に検討、議論され、逆に 平行線の公理がユークリッド幾何学の特徴的な仮定(仮説)で証明できない公理であることが明らかにされた。それとともに 数学とは何かに対する認識が根本的に変わり、数学とは公理系(仮説系)の上に建設された理論体系であって、絶対的な真理という概念を失った。
ここで焦点を当てたいのは 平行線の概念である。ユークリッド幾何学における平行線とは 任意の直線に対して、直線上以外の点を通って、それと交わらない直線のことで、平行線がただ1つ存在するというのがユークリッドの公理である。非ユークリッド幾何学では、そのような平行線が全然存在しなかったり、沢山存在する幾何学になっており、そのような幾何学は 実在し、現在も盛んに利用されている。
この平行線の問題が、ゼロ除算の発見1/0=0、台頭によって 驚嘆すべき、形相を帯びてきた。
ユークリッド自身、また、非ユークリッド幾何学の上記発見者たち、それに自ら深い研究をしていた天才ガウスにとっても驚嘆すべき事件であると考えられる。
何と ユークリッド空間で 平行線は ある意味で全て原点で交わっている という、現象が明らかにされた。
もちろん、ここで交わっていることの意味を 従来の意味にとれば、馬鹿馬鹿しいことになる。
そこで、その意味をまず、正確に述べよう。まずは、 イメージから述べる。リーマン球面に立体射影させると 全ユークリッド平面は 球面から北極点を除いた球面上に一対一に写される。そのとき、球面の北極点に対応する点が平面上になく、想像上の点として無限遠点を付け加えて対応させれば、立体射影における円、円対応を考えれば、平面上の平行線は無限遠点で交わっているとして、すっきりと説明され、複素解析学における基本的な世界観を与えている。平行線は無限遠点で 角ゼロ(度)で交わっている(接している)も立体射影における等角性で保証される。あまりの美しさのため、100年を超えて疑われることはなく、世の全ての文献はそのような扱いになっていて数学界の定説である。
ところがゼロ除算1/0=0では 無限遠点は空間の想像上の点として、存在していても、その点、無限遠点は数値では ゼロ(原点)に対応していることが明らかにされた。 すなわち、北極(無限遠点)は南極(原点)と一致している。そのために、平行線は原点で交わっていると解釈できる。もちろん、全ての直線は原点を通っている。
この現象はユークリッド空間の考えを改めるもので、このような性質は解析幾何学、微積分学、複素解析学、物理学など広範に影響を与え、統一的に新しい秩序ある世界を構成していることが明らかにされた。2200年を超えて、ユークリッド幾何学に全く新しい局面が現れたと言える。
平行線の交わりを考えてみる。交わる異なる2直線を1次方程式で書いて、交点の座標を求めて置く。その座標は、平行のとき、分母がゼロになって、交点の座標が求まらないと従来ではなっていたが、ゼロ除算では、それは可能で、原点(0,0)が対応すると解釈できる。ゼロ除算と解析幾何学からの帰結である。上記幾何学的な説明が、ゼロ除算で解析幾何学的にも導かれる。
一般の円の方程式を2次関数で表現すれば、(x^2+y^2) の係数がゼロの場合、直線の一般式になるが、ゼロ除算を用いると、それが保証されるばかりか、直線の中心は 原点である、直線も点円も曲率がゼロであることが導かれる。もちろん、ゼロ除算の世界では、全ての直線は原点を通っている。このとき、原点を無限遠点の映った影ともみなせ、原点はこのような意味で もともとの原点とこの意味での点としての、2重性を有し、この概念は今後大きな意味を有することになるだろう。
ゼロ除算1/0=0は ユークリッド幾何学においても、大きな変革を求めている。
以上
上記で、数学的に大事な観点は、ユークリッド自身そうであったが、平行線公理は真理で、証明されるべきもの、幾何学は絶対的な真理であると非ユークリッド幾何学の出現まで、考えられてきたということである。2000年を超える世界観であった事実である。そこで、平行線の公理を証明しようと多くの人が挑戦してきたが、非ユークリッド幾何学の出現まで不可能であった。実は、証明できない命題であったという全く意外な帰結であった。真に新しい、概念、世界観であった。証明できない命題の存在である。それこそ、世界観を変える、驚嘆すべき世界史上の事件であったと言える。
この事件に関してゼロ除算の発見は、全く異なる世界観を明らかにしている。ユークリッドそして、非ユークリッド幾何学の3人の発見者にとって、全く想像ができなかった、新しい事実である。平行線が 無限の先で交わっているとは ユークリッドは考えなかったと思われるが、近代では、無限の先で交わっていると考えられて来ている。― これには、アーベル、オイラー、リーマンなどの考えが存在する。このような考えは、ここ100年以上、世界の常識、定説になっている。ところがゼロ除算では、無限遠点は 数ではゼロが対応していて、平行線は代数的に原点で交わっている、すべての直線は代数的に原点を通っているという解釈が成り立つことを示している。
ユークリッドの幾何学の建設時の想い、ボーヤイ・ヤーノシュの激しい挑戦の様を、 想い を 深く、いろいろ想像している。
以 上
Matrices and Division by Zero z/0 = 0

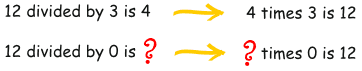
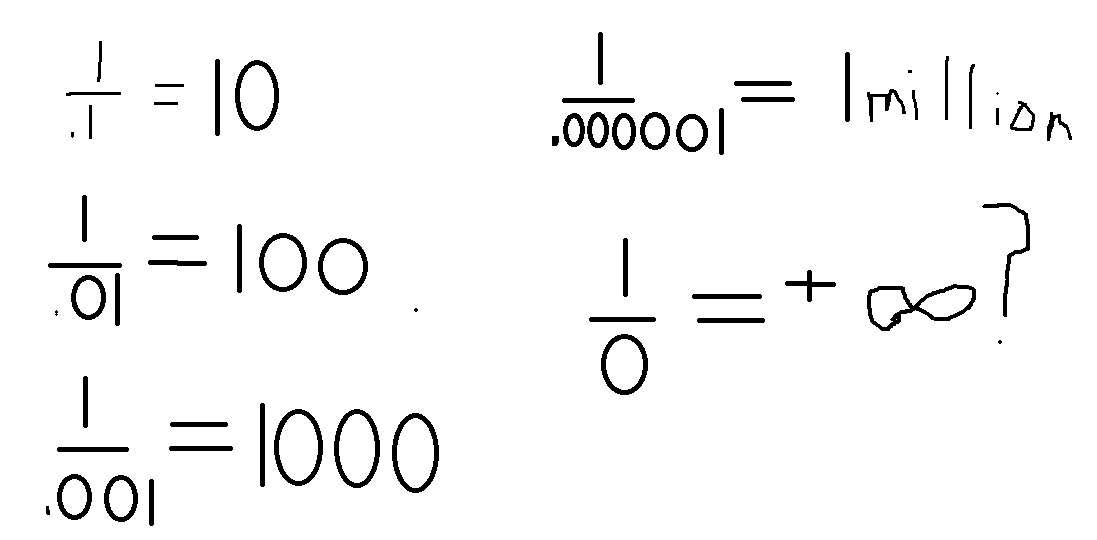
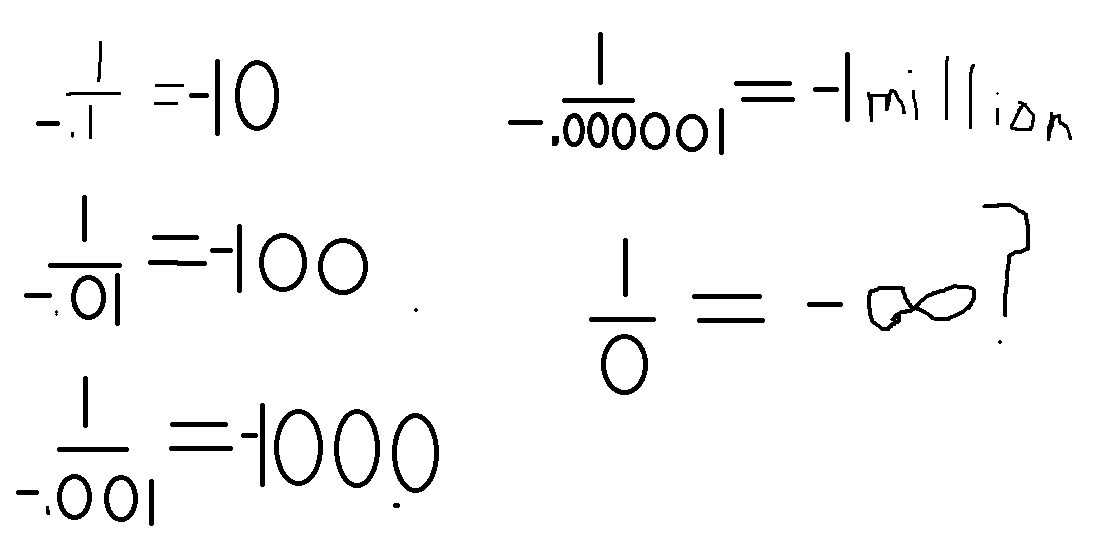

















































0 件のコメント:
コメントを投稿