バッハの音楽はどんな形？ 楽曲の中に潜む対称性について解説
東京カルチャーカルチャーにて開催された、数学への想いを語り合う女性限定イベント「ロマンティック数学ナイトガールズ」。最後に登壇したのは、高校時代に国際数学オリンピックで日本人女性として初めて金メダルを獲得した、ジャズピアニストの中島さち子氏。「バッハと対称性」というテーマで、バッハの楽譜に潜む対称性を取り上げ、エッシャーの絵画との比較やトポロジーとの関連などについて紹介しました。
- シリーズ
- ロマンティック数学ナイトガールズ > バッハと対称性2017年4月1日のログ
- スピーカー
- 中島さち子 氏
トピックス一覧
さらに表示
バッハの音楽に潜む対称性
中島さち子氏（以下、中島） 改めまして、こんにちは。今ご紹介いただきました中島さち子と申します。ロマンティック数学ナイト、実はかなり登壇させていただいていて、1回目と2回目、そして今日が私にとっては3回目になります。私は、今ご紹介いただいたように、ジャズピアノと即興・作曲が大好きです。ちょっとだけ宣伝をすると、実は最近『希望の花』というピアノトリオのCDを出しました。ついこの間リリースして、4月9日にはレコ発ライブをしているので、もしよかったらぜひいらしてください。amazon でもCDをご購入いただけます。ありがとうございます。一方で数学も大好きで、高校時代数学オリンピックに出たりなど、中高時代は本当に明け暮れていました。大学時代から数学と音楽に明け暮れるというような感じになりまして、今は数学と音楽と、そして教育の世界でいろいろ活動しています。私は「算数・数学の自由研究」の中央審査員もしているのですが、もし高校生の方がいらしたらはぜひ挑戦してみてください。数学って研究が難しいと思うかもしれないですけれど、やっぱり一番おもしろいのは研究の部分です。けっこう身近なところで、いろんなところに数学は使われているので、いろんなところから数学の種を発見してきて研究してもらうということを、今、促進しています。過去の自由研究作品は大人の方が見てもすごくおもしろいので、Webサイトに作品が載っているのでぜひ見てみてください。今日はなにをお話しようかと思っていたんですけれども、せっかくなので1回目2回目とまた違う話をしようと。実は、今日3番目にお話しされた佐々田先生と一緒に「数理女子」ワークショップを去年開催させていただきました。ここに、その時の写真が貼ってあります。数理女子企画ということで、女の子たちとお母さんたちと一緒にワークショップをしました。佐々田先生がお母さんのほう、私のほうが娘さんのほうを担当させていただき、多くのスタッフと一緒に開催しました。
全体テーマは「あなたも数学者」。サブテーマは「数学を発見する」と「数学で作る」。タイトルは「デザインの中に潜む数学」。より具体的にいうと、対称性というのが1つのキーワードになって、午前中はいろんな対称性を発見してもらいました。午後は対称性のアイディアを用いて作品を作るということをやって、非常に楽しかったですね。そのあと、改めて考えると、対称性って音楽のなかにもいっぱいあることに気づきました。とくに対称性をよく用いているのがバッハですね。今日は「バッハと対称性」という、すごく恐れ多いプレゼンタイトルをつけてるんですけれども（笑）。バッハの音楽には、対称性がいっぱいあります。これは本当に一例です。たぶん聴いたことがある曲だと思うんですけれども。（ピアノで「2声のインベンション BWV 772 」のフレーズを演奏）こういう。きっと聴いたことありますよね。このあとに左手が同じように。（左手のパートを演奏）ここまでが同じフレーズが1オクターブ平行移動して同じ音名で進みます。今度はそれが5度平行移動しまして。（平行移動したフレーズを演奏）左手もまた平行移動していって。今度はそれをこの横の線でパタンと裏返しにしたようなかたちが次に続いていきます。（裏返しにしたフレーズを演奏）下のほうはどうなっていくかというと、それがちょっと2倍になって、本当に一部ですけれど、ものすごく簡単なところですけれど、ドレミファというところを2倍にしたかたちがスライドして、こう並んでいる。
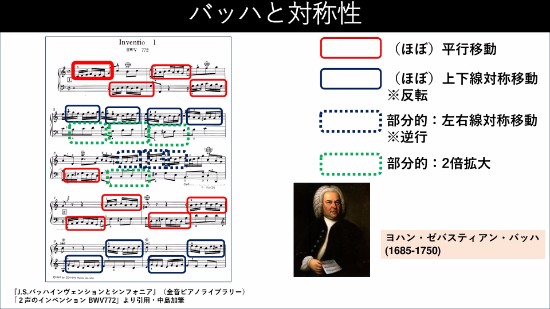このように、バッハという音楽家は平行移動とか線対称移動とか、回転は難しいけれど、あとは拡大縮小とか、そういう対称性をたくさん使って作曲している人なのですね。だから「あ、おもしろいな」と。「改めてバッハを見てみると対称性がいっぱいあるな」と。私自身、やっぱり作曲するときに、なにかモチーフが思いついて、それを発展させていくんですけれど、そこに対称性などを利用することがやっぱりあります。とくに自分が行き詰まってスランプに陥ったときは、あえてそういう数学的なことをいろいろ考えて新しい次の一歩を探すということがありました。今日はせっかくなので、今ちょうど佐々木さんからお話のあったトポロジーとも関係させて、各々の楽譜がどんな軌道空間というか、どんな形を指し示しているのかって、ちょっと数学と絡めながら見てみようと思います。
全体テーマは「あなたも数学者」。サブテーマは「数学を発見する」と「数学で作る」。タイトルは「デザインの中に潜む数学」。より具体的にいうと、対称性というのが1つのキーワードになって、午前中はいろんな対称性を発見してもらいました。午後は対称性のアイディアを用いて作品を作るということをやって、非常に楽しかったですね。そのあと、改めて考えると、対称性って音楽のなかにもいっぱいあることに気づきました。とくに対称性をよく用いているのがバッハですね。今日は「バッハと対称性」という、すごく恐れ多いプレゼンタイトルをつけてるんですけれども（笑）。バッハの音楽には、対称性がいっぱいあります。これは本当に一例です。たぶん聴いたことがある曲だと思うんですけれども。（ピアノで「2声のインベンション BWV 772 」のフレーズを演奏）こういう。きっと聴いたことありますよね。このあとに左手が同じように。（左手のパートを演奏）ここまでが同じフレーズが1オクターブ平行移動して同じ音名で進みます。今度はそれが5度平行移動しまして。（平行移動したフレーズを演奏）左手もまた平行移動していって。今度はそれをこの横の線でパタンと裏返しにしたようなかたちが次に続いていきます。（裏返しにしたフレーズを演奏）下のほうはどうなっていくかというと、それがちょっと2倍になって、本当に一部ですけれど、ものすごく簡単なところですけれど、ドレミファというところを2倍にしたかたちがスライドして、こう並んでいる。このように、バッハという音楽家は平行移動とか線対称移動とか、回転は難しいけれど、あとは拡大縮小とか、そういう対称性をたくさん使って作曲している人なのですね。だから「あ、おもしろいな」と。「改めてバッハを見てみると対称性がいっぱいあるな」と。私自身、やっぱり作曲するときに、なにかモチーフが思いついて、それを発展させていくんですけれど、そこに対称性などを利用することがやっぱりあります。とくに自分が行き詰まってスランプに陥ったときは、あえてそういう数学的なことをいろいろ考えて新しい次の一歩を探すということがありました。今日はせっかくなので、今ちょうど佐々木さんからお話のあったトポロジーとも関係させて、各々の楽譜がどんな軌道空間というか、どんな形を指し示しているのかって、ちょっと数学と絡めながら見てみようと思います。対称性のある音楽の“形”
これは一番簡単な例です。
回文みたいなものです。ちなみに、この回文は、回文を作らなきゃいけない時があって、家族で一生懸命作って。家族が「うろたえたろう」というのを作ったんですけれど（笑）。そして、これはかえるのうたの最初のフレーズですね。（ピアノで「かえるのうた」のメロディを演奏）これ、あえて小節線とか省いて書くと回文みたいになっています。回文構造のフレーズは意外に音楽的になることも多くて。例えば右側、適当に作ったフレーズですけれども。（適当に作ったフレーズを演奏）それを逆にすると……。（逆にして演奏）これに和音などをつければ、なにかしらちょっと曲らしきものになってきますよね。回文構造では右左まったく同じものが左右対称に鏡像になっているので、同じ部分をペタッっと貼り合わせてあげると、長方形みたいな形が見えてきます。もしこの回文フレーズを両手で同時に弾くと。（両手で同じフレーズを演奏）すると、さらにこの長方形の上の辺と下の辺を同一視してくっつけることができるので、長方形から輪っかになりますね。「だからどうした？」っていう気もしますが……。でも、対称性の違いをこのように空間として見える化していくというのは、なかなかおもしろくて。さらに、さっきは線対称でしたが、今度は180度回転、つまり点対称ですね。点対称にするとどうなるか？ もちろんこの譜面、ちょっと音符の線が左についてるので変なんですけれど、そこはちょっとおいておくと、例えば元のフレーズは……。（元のフレーズを演奏）これの180度回転させたのを弾くと、ちょっと上になります。（180度回転、点対称させたフレーズを演奏）こんな感じになるわけです。これと似た構造を持つものがこの譜面です。モーツァルト作と巷で言われていますが、たぶん本当はモーツァルトではない人が作った曲ですね。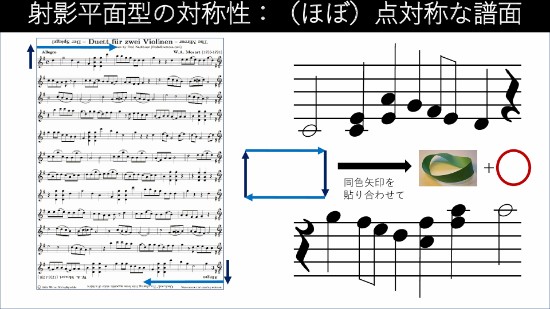
あるフレーズをちょうどくるっと上下逆にすると、シがこの線対称移動に関してちょうど軸になるので。（ピアノ演奏）というフレーズが……。（ピアノ演奏）に変わるので、この曲は……。（ピアノ演奏）こんな感じで始まるんですけれど。この一番右下のところから読んでみると……。（ピアノ演奏）という感じで、似たような感じになるので、実は左上と右下の両方から同時に弾いてもなかなかおもしろい曲になる、というような曲が知られています。これちょっと見ると、実はちゃんと点対称にはなってないんですが、でも、アイデアとしては点対称で作ろうとしている曲ですね。これは数学的にどうなるかというと、出ました。実はけっこう難しくて、射影平面なんです。さっき、これを知ってる人はなかなかって言われたんですけど。断面図はとても簡単で、メビウスの帯ってみなさんご存じだと思うんですけれど、上が→方向で下が←方向だから、右上と左下が一緒になって、左上と右下が一緒になるようにこう結ぶと、メビウスの帯という向き付けができないような、境界ありの曲面ができます。そこでさらに、こことここを結ぼうと思うとできないんですね。ここはこっち側向き、こっちはこっち向き。3次元空間ではできないんですけれど、ちょっと考えてみて、なかに円盤を1回くり抜いてからグニュグニュって動かしていって、ちょっと頭をやわらかくして動かしていって、つなげてみると、実はメビウスの帯ができます。なので、射影平面というのは、メビウスの帯のこの上のところをずるずるってこのアリさんがこの縁を歩いていったときに、その縁に沿って心の目で円盤をくっつけてあげるんです。ぐにゃぐにゃっとすごく曲がる円盤を。しかも3次元では無理なので、ちょっと次元を上げていただいて、くっつけて合わせてあげると見えてくるのが射影平面。複雑にいうと、この音楽は射影平面の音楽だと言えると思います。
回文みたいなものです。ちなみに、この回文は、回文を作らなきゃいけない時があって、家族で一生懸命作って。家族が「うろたえたろう」というのを作ったんですけれど（笑）。そして、これはかえるのうたの最初のフレーズですね。（ピアノで「かえるのうた」のメロディを演奏）これ、あえて小節線とか省いて書くと回文みたいになっています。回文構造のフレーズは意外に音楽的になることも多くて。例えば右側、適当に作ったフレーズですけれども。（適当に作ったフレーズを演奏）それを逆にすると……。（逆にして演奏）これに和音などをつければ、なにかしらちょっと曲らしきものになってきますよね。回文構造では右左まったく同じものが左右対称に鏡像になっているので、同じ部分をペタッっと貼り合わせてあげると、長方形みたいな形が見えてきます。もしこの回文フレーズを両手で同時に弾くと。（両手で同じフレーズを演奏）すると、さらにこの長方形の上の辺と下の辺を同一視してくっつけることができるので、長方形から輪っかになりますね。「だからどうした？」っていう気もしますが……。でも、対称性の違いをこのように空間として見える化していくというのは、なかなかおもしろくて。さらに、さっきは線対称でしたが、今度は180度回転、つまり点対称ですね。点対称にするとどうなるか？ もちろんこの譜面、ちょっと音符の線が左についてるので変なんですけれど、そこはちょっとおいておくと、例えば元のフレーズは……。（元のフレーズを演奏）これの180度回転させたのを弾くと、ちょっと上になります。（180度回転、点対称させたフレーズを演奏）こんな感じになるわけです。これと似た構造を持つものがこの譜面です。モーツァルト作と巷で言われていますが、たぶん本当はモーツァルトではない人が作った曲ですね。あるフレーズをちょうどくるっと上下逆にすると、シがこの線対称移動に関してちょうど軸になるので。（ピアノ演奏）というフレーズが……。（ピアノ演奏）に変わるので、この曲は……。（ピアノ演奏）こんな感じで始まるんですけれど。この一番右下のところから読んでみると……。（ピアノ演奏）という感じで、似たような感じになるので、実は左上と右下の両方から同時に弾いてもなかなかおもしろい曲になる、というような曲が知られています。これちょっと見ると、実はちゃんと点対称にはなってないんですが、でも、アイデアとしては点対称で作ろうとしている曲ですね。これは数学的にどうなるかというと、出ました。実はけっこう難しくて、射影平面なんです。さっき、これを知ってる人はなかなかって言われたんですけど。断面図はとても簡単で、メビウスの帯ってみなさんご存じだと思うんですけれど、上が→方向で下が←方向だから、右上と左下が一緒になって、左上と右下が一緒になるようにこう結ぶと、メビウスの帯という向き付けができないような、境界ありの曲面ができます。そこでさらに、こことここを結ぼうと思うとできないんですね。ここはこっち側向き、こっちはこっち向き。3次元空間ではできないんですけれど、ちょっと考えてみて、なかに円盤を1回くり抜いてからグニュグニュって動かしていって、ちょっと頭をやわらかくして動かしていって、つなげてみると、実はメビウスの帯ができます。なので、射影平面というのは、メビウスの帯のこの上のところをずるずるってこのアリさんがこの縁を歩いていったときに、その縁に沿って心の目で円盤をくっつけてあげるんです。ぐにゃぐにゃっとすごく曲がる円盤を。しかも3次元では無理なので、ちょっと次元を上げていただいて、くっつけて合わせてあげると見えてくるのが射影平面。複雑にいうと、この音楽は射影平面の音楽だと言えると思います。バッハの音楽とエッシャーの絵画
あともう1つ有名なのが、その前にもう1個。さっき出てきましたトーラス。トーラスの音楽もあります。これは絵なんですけれど、今日はあえてあんまり名前を出していないのですが、エッシャーという画家さんがいて、数学を使ったおもしろい絵をいろいろ描かれています。今日は、エッシャーを真似して、例の数理女子ワークショップの事前準備で作った作品をいくつか持ってきました。
ここには右側方向の平行移動と下側方向の2つの平行移動があります。それを断面図で描くとこういう矢印になっているので、これをクルッてくっつけて、ここもクルッとくっつけるとちょうどグニャグニャっと伸ばしていただくとわかると思うんですけれど、こういう浮き輪みたいな状態になります。これはだからドーナツ型の対称性を持つ音楽。さっきのバッハの曲でも、最初のところはまさにそうなってる。（ピアノ演奏）ここで4つ出てくるんですけれど、この動きというのはちょうどきれいに平行四辺形になるようにできあがっていて、これを貼り合わせてみると、ちょうどドーナツ型になっているよという感じですね。もう1個。これはかなり有名な『蟹のカノン』と呼ばれるバッハの曲です。
これどうできているかというと、見ていただくとわかるのですが、右手が始まっていって終わるまでを読んで、今度この左手をこっちから読んでみるとまったく同じになってるんですね。まったく同じになっている。これ、私、実はこの構造とまったく同じ対称性を持つ絵はこれ、エッシャーの『騎乗者』なんですね。いろいろ考えましたが、実は『Crab Canon』に触発されて、エッシャーは『Crab Canon』という蟹の絵を描いてるんですけれど、対称性としてはちょっと違っていて。この対称性は、人がこっち向いて乗ってる絵を左右対称にしてからずるずるってずらしたような対称性です。これは「すべり鏡映」という対称性なのですが、バッハの蟹のカノンもすべり鏡映になっています。上段を左右対称移動させてから下段にずらしました。
とくに今日、例えばこれ、右手と左手を1オクターブずらすとまさに平行移動していることになるので、こういうかたちになっていて、右手はこうやって読んでいくんですけど、左手でこうやって読んだときとまったく同じ絵になっている。右手がこうやって読んでいったときと、左手がここから、最後から読み直していったときがまったく同じ絵になっている。これはどんなものかというと、貼り合わせとしては、上下は右手が入れ替わっているように見えるんですけれど、上と下の関係は変わっていない、ト音記号の上は上であるという状況は変わっていないので、これは実はさっきの射影平面とはちょっと違っていて。これは、こことここが逆になっているけれど、こことここが同じということで。それをやってみると、これもやっぱり3次元でできない図形なんですけれど、クラインの壺ですね。クラインの壺が今日は大人気ですけれど、この譜面の対称性はクラインの壺になると。これはもちろん片方だけ貼り合わせればメビウスの帯になります。メビウスの帯2個分のものと考えていただいて。これとこれを貼り合わせると、これになります。というふうに、ちょっと空間を見ながら考えるとけっこうおもしろいなと思いました。ちなみに、この『Crab Canon』、せっかくだからちょっとだけ演奏してみようかなと思います。なかなかきれいな曲なんです。すぐ終わるので、ちょっとだけ弾いてみますね。（ピアノで『Crab Canon』を演奏）という曲です。（会場拍手）ありがとうございます。覚えていないので、これ見ながらやりましたが。今の例えば最後のところが……。（ピアノ演奏）これが最初だと……。（ピアノ演奏）すごくきれいにできていて、やっぱりさすがバッハだなと。けっこうバッハらしいフレージングとか、あとちょっと盛り上がっていくところとかが、うまいこと前半後半に右手と左手が違うかたちで出てくる。同じかたちを逆に読んでるだけなんですけれども、前半後半では素材は同じものなのに左右対称、上下が入れ替えになるだけで雰囲気が全然違っているというのがすごいおもしろい作品です。だから、これはクラインの壺なんですね。
ここには右側方向の平行移動と下側方向の2つの平行移動があります。それを断面図で描くとこういう矢印になっているので、これをクルッてくっつけて、ここもクルッとくっつけるとちょうどグニャグニャっと伸ばしていただくとわかると思うんですけれど、こういう浮き輪みたいな状態になります。これはだからドーナツ型の対称性を持つ音楽。さっきのバッハの曲でも、最初のところはまさにそうなってる。（ピアノ演奏）ここで4つ出てくるんですけれど、この動きというのはちょうどきれいに平行四辺形になるようにできあがっていて、これを貼り合わせてみると、ちょうどドーナツ型になっているよという感じですね。もう1個。これはかなり有名な『蟹のカノン』と呼ばれるバッハの曲です。これどうできているかというと、見ていただくとわかるのですが、右手が始まっていって終わるまでを読んで、今度この左手をこっちから読んでみるとまったく同じになってるんですね。まったく同じになっている。これ、私、実はこの構造とまったく同じ対称性を持つ絵はこれ、エッシャーの『騎乗者』なんですね。いろいろ考えましたが、実は『Crab Canon』に触発されて、エッシャーは『Crab Canon』という蟹の絵を描いてるんですけれど、対称性としてはちょっと違っていて。この対称性は、人がこっち向いて乗ってる絵を左右対称にしてからずるずるってずらしたような対称性です。これは「すべり鏡映」という対称性なのですが、バッハの蟹のカノンもすべり鏡映になっています。上段を左右対称移動させてから下段にずらしました。とくに今日、例えばこれ、右手と左手を1オクターブずらすとまさに平行移動していることになるので、こういうかたちになっていて、右手はこうやって読んでいくんですけど、左手でこうやって読んだときとまったく同じ絵になっている。右手がこうやって読んでいったときと、左手がここから、最後から読み直していったときがまったく同じ絵になっている。これはどんなものかというと、貼り合わせとしては、上下は右手が入れ替わっているように見えるんですけれど、上と下の関係は変わっていない、ト音記号の上は上であるという状況は変わっていないので、これは実はさっきの射影平面とはちょっと違っていて。これは、こことここが逆になっているけれど、こことここが同じということで。それをやってみると、これもやっぱり3次元でできない図形なんですけれど、クラインの壺ですね。クラインの壺が今日は大人気ですけれど、この譜面の対称性はクラインの壺になると。これはもちろん片方だけ貼り合わせればメビウスの帯になります。メビウスの帯2個分のものと考えていただいて。これとこれを貼り合わせると、これになります。というふうに、ちょっと空間を見ながら考えるとけっこうおもしろいなと思いました。ちなみに、この『Crab Canon』、せっかくだからちょっとだけ演奏してみようかなと思います。なかなかきれいな曲なんです。すぐ終わるので、ちょっとだけ弾いてみますね。（ピアノで『Crab Canon』を演奏）という曲です。（会場拍手）ありがとうございます。覚えていないので、これ見ながらやりましたが。今の例えば最後のところが……。（ピアノ演奏）これが最初だと……。（ピアノ演奏）すごくきれいにできていて、やっぱりさすがバッハだなと。けっこうバッハらしいフレージングとか、あとちょっと盛り上がっていくところとかが、うまいこと前半後半に右手と左手が違うかたちで出てくる。同じかたちを逆に読んでるだけなんですけれども、前半後半では素材は同じものなのに左右対称、上下が入れ替えになるだけで雰囲気が全然違っているというのがすごいおもしろい作品です。だから、これはクラインの壺なんですね。
音楽以外の分野に見る対称性
というように、最近なんかだんだんマニアックに楽譜を眺めるようになってきました。ちなみに、ワークショップのときは、ほかにも回転対称性を持つような作品も扱いました。楽譜では、なかなかまだ180度以外の回転対称性を発見することはできていないのですが。例えば、こんな形だと、ここに実は120度回転対称性があるとか、ここには120度回転対称性。これも120度回転対称性。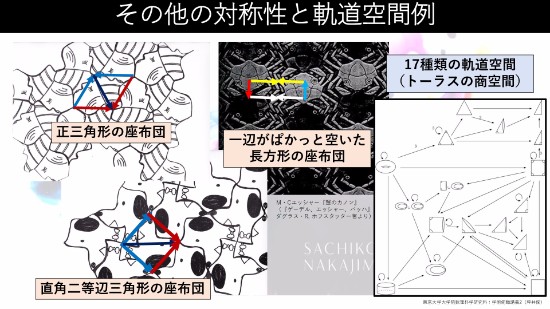
同じところ、例えば、頭のこの帽子のところを同じだとみなして貼り合わせるとか、おしりの部分を貼り合わせるとかやってみると、ちょうど正三角形の座布団みたいな空間になるんですね。だから、この対称性を表す軌道空間は正三角形の座布団だというふうに見えてくると。同じように、こういうスヌーピーみたいな絵なんですけれども、ここに実は180度回転対称性が1個あって、90度回転対称性が2個あって、それをやっぱり同じ点は同じだと見なすという。なにを同じと思うかというのはけっこう数学は本当に自由なので、そういうかたちで結んでいくと、これは直角二等辺三角形の座布団とかできたり。この蟹はいろいろ考えていくと、1つのものの見方としては、こんなかたちで結べて。ところが、こことここは、この点とこの点が一緒で、この点とこの点が一緒なんですが、くっつけてみると、長方形の座布団なんだけど、1点だけパカっと開いてるような軌道空間が見えてきたりするんですね。こういう繰り返し模様の作品は対称性、線対称とか点対称とか、さらにはその奥に実は位相空間というものが実は関連していて、この対称性を表している空間ってどんな形なんだろうというのがトポロジーの話とかとつながってきたり。実は2方向の平行移動対称性を持つような平面上の対称性は、17種類しかないんだよってことが証明されています。空間だと230種類あるんですけれども。そのあたり本当におもしろい神秘的な世界なので、私はワークショップを通して、自分自身も勉強しながら、「あ、音楽にするとこれはこういうふうになってるいるな」とか感じるようになりました。自分が音楽を作るときも、対称性のアイディアだけで作ってしまうとやっぱり幅が狭まっちゃうんですけれども、「対称性をヒントにしながら、マンネリ化してきたら新しい対称性のフレーズを作ってみよう」とかいうかたちで作ったりしています。対称性というのは本当に大事なもので、数学とか音楽だけではなく、生物、化学や建築の世界にも現れています。ご存じかもしれませんけれども、ダイヤモンドとかっていうのは全部C、炭素原子でできているのですが、つなぎ方、つまり対称性がちょっと違うだけでまったく違うものに切り替わってしまう。このようにダイヤモンド結晶のつなぎ方にするのか、あるいはこういう蜂の巣みたいなものを縦に並べるような形で作るのか、これだけで美しさも違えば強さも全く変わってしまいます。
だから、対称性とかどんなつながり方になってるかというのはとても大事な要素になります。だから、ものが「なにからできているか」だけじゃなくて、「どんな関係・構造からできているか」ということが、ものごとの性質を見る際には極めて大切なものなんですね。対称性というのはアートやデザインの世界、建築の世界とかにも関係します。
同じところ、例えば、頭のこの帽子のところを同じだとみなして貼り合わせるとか、おしりの部分を貼り合わせるとかやってみると、ちょうど正三角形の座布団みたいな空間になるんですね。だから、この対称性を表す軌道空間は正三角形の座布団だというふうに見えてくると。同じように、こういうスヌーピーみたいな絵なんですけれども、ここに実は180度回転対称性が1個あって、90度回転対称性が2個あって、それをやっぱり同じ点は同じだと見なすという。なにを同じと思うかというのはけっこう数学は本当に自由なので、そういうかたちで結んでいくと、これは直角二等辺三角形の座布団とかできたり。この蟹はいろいろ考えていくと、1つのものの見方としては、こんなかたちで結べて。ところが、こことここは、この点とこの点が一緒で、この点とこの点が一緒なんですが、くっつけてみると、長方形の座布団なんだけど、1点だけパカっと開いてるような軌道空間が見えてきたりするんですね。こういう繰り返し模様の作品は対称性、線対称とか点対称とか、さらにはその奥に実は位相空間というものが実は関連していて、この対称性を表している空間ってどんな形なんだろうというのがトポロジーの話とかとつながってきたり。実は2方向の平行移動対称性を持つような平面上の対称性は、17種類しかないんだよってことが証明されています。空間だと230種類あるんですけれども。そのあたり本当におもしろい神秘的な世界なので、私はワークショップを通して、自分自身も勉強しながら、「あ、音楽にするとこれはこういうふうになってるいるな」とか感じるようになりました。自分が音楽を作るときも、対称性のアイディアだけで作ってしまうとやっぱり幅が狭まっちゃうんですけれども、「対称性をヒントにしながら、マンネリ化してきたら新しい対称性のフレーズを作ってみよう」とかいうかたちで作ったりしています。対称性というのは本当に大事なもので、数学とか音楽だけではなく、生物、化学や建築の世界にも現れています。ご存じかもしれませんけれども、ダイヤモンドとかっていうのは全部C、炭素原子でできているのですが、つなぎ方、つまり対称性がちょっと違うだけでまったく違うものに切り替わってしまう。このようにダイヤモンド結晶のつなぎ方にするのか、あるいはこういう蜂の巣みたいなものを縦に並べるような形で作るのか、これだけで美しさも違えば強さも全く変わってしまいます。だから、対称性とかどんなつながり方になってるかというのはとても大事な要素になります。だから、ものが「なにからできているか」だけじゃなくて、「どんな関係・構造からできているか」ということが、ものごとの性質を見る際には極めて大切なものなんですね。対称性というのはアートやデザインの世界、建築の世界とかにも関係します。数学はものの見方を広げてくれる
いろいろ話してきましたけれども、私自身は数学と音楽をやっておりまして、私は数学も音楽もすごいクリエイティブな世界だと思っています。ものの見方を変えることができるのが、数学の自由さでありおもしろいところだと思っていて、音楽のおもしろさも同じだと思うんですよね。1つのものを、例えば同じドでも、（ピアノを鳴らして）この中のドなのか、この中のドなのかとかがいろいろ違う。数学においても、これは例えば前から見て三角形だったとしても、もしかしたら横から見たらぜんぜん違うかもしれない。上から見るとぜんぜん違うかもしれない。そんな感じで、数学というのはものの見方をいろんな方向に広げてくれる。論理の力と感性の力がお互いに拮抗するかたちでいろんな新しいものが見えてくる。数学の新しい発見、芸術における新しい創造とか、そういうものというのはすごくリンクしているなと感じています。もうこれでもうそろそろ時間なんですけれども、せっかくなのでちょっと1個ぐらい演奏をしたいなと思っていまして。大丈夫ですか。ありがとうございます。演奏といっても、これ1回目に登壇した際にもやらせてもらった内容なんですけれども、みなさんから音をいただいて、その5音を基準にして即興演奏をしたいと思います。その5音の味付けの仕方にはいろんな方向があります。ちょっとリズムを変えたり、和音を変えたりとか、いろんな変え方によって5音の雰囲気ががらりと変わる。今日は初めてそれをちょっとリフレクション、線対称移動をさせたもの、逆から読んだものも交えながらやれたらいいなと思っているので、5音をいただきたいと思います。例えば、ミとかファとかラ♭とか、そんな音をください。先着順にします。「ミ」とか言ってください。参加者1 ソの♯。中島 ソの♯。ありがとうございます。あと4つ。参加者2 レ♭。中島 レ♭。なんかやっぱり数学好きな人たちですね（笑）。これね、難易度が毎回違うんですね。あとはなんでしょう？ 3つ。参加者3 A。中島 Aですか？ ラ。おお、Aと言ってくるあたりがかっこいいですね。あと2つ。参加者4 ファの♯。中島 ファの♯。♯が好きですね。みなさん。♯と♭と（笑）。あともう1個お願いします。どなたでも。参加者5 じゃあ、トで。中島 ト……そういうのがくるんですねえ。ドって変えちゃいけないですね。ト。ちょっとドがなんか小さく鳴っている感じで。昔ちっちゃい子がいた時に「かたつむり！」って言われたことがあって、かたつむりを……。（かたつむりっぽい音を鳴らす）そういうのでごまかしながらやるという演奏をしたことがあります（笑）。えーと、今いただいた5つの音が、なんかすごい不思議な音になっていて。（5つの音を鳴らす）あ、でも、なんかきれいですね。これトです。ドじゃなくて（笑）。それを逆から単純に読んだだけだと……。（5つの音を逆から鳴らす）なんだろう。ちょっと最初は普通というか、すごくこれだけで音楽になっている感じなんですけど。なんかちょっと不思議な感じですね。ということで、さらになにか上下の線対称もしようかと思ったんですけど、ちょっとあまり無理をせずに左側と右側から読むという2つで、それを散りばめながら、実際はほかの音も使っていきますけれども、ちょっと即興演奏をしてみたいと思います。（即興でピアノ演奏）（会場拍手）中島 ありがとうございます。今日は対称性とバッハというテーマでお話させていただきました、本日またみなさんとこのあともいろいろしゃべれるのを楽しみにしています。よろしくお願いします。（会場拍手）http://logmi.jp/211785
とても興味深く読みました：バッハとゼロ除算の関係は・・・
ベートーヴェンは多少なりとも
再生核研究所声明 382 (2017.9.11)： ニュートンを越える天才たちに－育成する立場の人に
次のような文書を残した： いま思いついたこと：ニュートンは偉く、ガウス、オイラーなども 遥かに及ばないと 何かに書いてあると言うのです。それで、考え、思いついた。 ガウス、オイラーの業績は とても想像も出来なく、如何に基本的で、深く、いろいろな結果がどうして得られたのか、思いもよらない。まさに天才である。数学界にはそのような天才が、結構多いと言える。しかるに、ニュートンの業績は 万有引力の法則、運動の法則、微積分学さえ、理解は常人でも出来き、多くの数学上の結果もそうである。しかるにその偉大さは 比べることも出来ない程であると表現されると言う。それは、どうしてであろうか。確かに世界への甚大な影響として 納得できる面がある。－ 初めて スタンフォード大学を訪れた時、確かにニュートンの肖像画が 別格高く掲げられていたことが、鮮明に想い出されてくる。－ 今でもそうであろうか？（２０１７．９．８．１０：４２）。
万物の運動を支配する法則、力、エネルギーの原理、長さ、面積、体積を捉え、傾き、勾配等の概念を捉えたのであるから、森羅万象のある基礎部分をとらえたものとして、世界史における影響が甚大であると考えれば その業績の大きさに驚かされる。
世界史における甚大な影響として、科学上ではないが、それらを越える、宗教家の大きな存在に まず、注意を喚起して置きたい。数学者、天文学者では ゼロを数として明確に導入し、負の数も考え、算術の法則（四則演算）を確立し、ゼロ除算0/0=0を宣言したBrahmagupta (598 -668 ?) の 偉大な影響 にも特に注意したい。
そのように偉大なるニュートンを発想すれば、それを越える偉大なる歴史上の存在の可能性を考えたくなるのは人情であろう。そこで、天才たちやそれを育成したいと考える人たちに 如何に考えるべきかを述べて置きたい。
万人にとって近い存在で、甚大な貢献をするであろう、科学的な分野への志向である。鍵は 生命と情報ではないだろうか。偉大なる発見、貢献であるから具体的に言及できるはずがない。しかしながら、科学が未だ十分に達しておらず、しかも万人に甚大な影響を与える科学の未知の分野として、生命と情報分野における飛躍的な発見は ニュートンを越える発見に繋がるのではないだろうか。
生物とは何者か、どのように作られ、どのように活動しているか、本能と環境への対応の原理を支配する科学的な体系、説明である。生命の誕生と終末の後、人間精神の在り様と物理的な世界の関係、殆ど未知の雄大な分野である。
情報とは何か、情報と人間の関係、影響、発展する人工知能の方向性とそれらを統一する原理と理論。情報と物の関係。情報が物を動かしている実例が存在する。
それらの分野における画期的な成果は ニュートンを越える世界史上の発見として出現するのではないだろうか。
これらの難解な課題においてニュ－トンの場合の様に常人でも理解できるような簡明な法則が発見されるのではないだろうか。
人類未だ猿や動物にも劣る存在であるとして、世界史を恥ずかしい歴史として、未来人は考え、評価するだろう。世の天才たちの志向について、またそのような偉大なる人材を育成する立場の方々の注意を喚起させたい。偉大なる楽しい夢である。
それにはまずは、世界史を視野に、人間とは何者かと問い、神の意思を捉えようとする真智への愛を大事に育てて行こうではないか。
以 上
再生核研究所声明353（2017.2.2） ゼロ除算 記念日
2014.2.2 に 一般の方から100/0 の意味を問われていた頃、偶然に執筆中の論文原稿にそれがゼロとなっているのを発見した。直ぐに結果に驚いて友人にメールしたり、同僚に話した。それ以来、ちょうど３年、相当詳しい記録と経過が記録されている。重要なものは再生核研究所声明として英文と和文で公表されている。最初のものは
再生核研究所声明 148（2014.2.12）: 100/0=0, 0/0=0 － 割り算の考えを自然に拡張すると ― 神の意志
で、最新のは
Announcement 352 (2017.2.2): On the third birthday of the division by zero z/0=0
である。
アリストテレス、ブラーマグプタ、ニュートン、オイラー、アインシュタインなどが深く関与する ゼロ除算の神秘的な永い歴史上の発見であるから、その日をゼロ除算記念日として定めて、世界史を進化させる決意の日としたい。ゼロ除算は、ユークリッド幾何学の変更といわゆるリーマン球面の無限遠点の考え方の変更を求めている。― 実際、ゼロ除算の歴史は人類の闘争の歴史と共に 人類の愚かさの象徴であるとしている。
心すべき要点を纏めて置きたい。
１） ゼロの明確な発見と算術の確立者Brahmagupta (598 - 668 ?) は 既にそこで、0/0=0 と定義していたにも関わらず、言わば創業者の深い考察を理解できず、それは間違いであるとして、１３００年以上も間違いを繰り返してきた。
２） 予断と偏見、慣習、習慣、思い込み、権威に盲従する人間の精神の弱さ、愚かさを自戒したい。我々は何時もそのように囚われていて、虚像を見ていると 真智を愛する心を大事にして行きたい。絶えず、それは真かと 問うていかなければならない。
３） ピタゴラス派では 無理数の発見をしていたが、なんと、無理数の存在は自分たちの世界観に合わないからという理由で、― その発見は都合が悪いので ― 、弟子を処刑にしてしまったという。真智への愛より、面子、権力争い、勢力争い、利害が大事という人間の浅ましさの典型的な例である。
４） この辺は、２０００年以上も前に、既に世の聖人、賢人が諭されてきたのに いまだ人間は生物の本能レベルを越えておらず、愚かな世界史を続けている。人間が人間として生きる意義は 真智への愛にある と言える。
５） いわば創業者の偉大な精神が正確に、上手く伝えられず、ピタゴラス派のような対応をとっているのは、本末転倒で、そのようなことが世に溢れていると警戒していきたい。本来あるべきものが逆になっていて、社会をおかしくしている。
６） ゼロ除算の発見記念日に 繰り返し、人類の愚かさを反省して、明るい世界史を切り拓いて行きたい。
以 上
追記：
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
再生核研究所声明371（2017.6.27）ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告
http://ameblo.jp/syoshinoris/theme-10006253398.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html
再生核研究所声明 375 (2017.7.21)：ブラックホール、ゼロ除算、宇宙論
本年はブラックホール命名５０周年とされていたが、最近、wikipedia で下記のように修正されていた：
名称[編集]
"black hole"という呼び名が定着するまでは、崩壊した星を意味する"collapsar"[1]（コラプサー）などと呼ばれていた。光すら脱け出せない縮退星に対して "black hole" という言葉が用いられた最も古い印刷物は、ジャーナリストのアン・ユーイング (Ann Ewing) が1964年1月18日の Science News-Letter の "'Black holes' in space" と題するアメリカ科学振興協会の会合を紹介する記事の中で用いたものである[2][3][4]。一般には、アメリカの物理学者ジョン・ホイーラーが1967年に "black hole" という名称を初めて用いたとされるが[5]、実際にはその年にニューヨークで行われた会議中で聴衆の一人が洩らした言葉をホイーラーが採用して広めたものであり[3]、またホイーラー自身は "black hole" という言葉の考案者であると主張したことはない[3]。https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%A9%E3%83%83%E3%82%AF%E3%83%9B%E3%83%BC%E3%83%AB
世界は広いから、情報が混乱することは よく起きる状況がある。ブラックホールの概念と密接な関係のあるゼロ除算の発見（２０１４．２．２）については、歴史的な混乱が生じないようにと 詳しい経緯、解説、論文、公表過程など記録するように配慮してきた。
ゼロ除算は簡単で自明であると初期から述べてきたが、問題はそこから生じるゼロ除算算法とその応用であると述べている。しかし、その第１歩で議論は様々でゼロ除算自身についていろいろな説が存在して、ゼロ除算は現在も全体的に混乱していると言える。インターネットなどで参照出来る膨大な情報は、我々の観点では不適当なものばかりであると言える。もちろん学術界ではゼロ除算発見後３年を経過しているものの、古い固定観念に囚われていて、新しい発見は未だ認知されているとは言えない。最近国際会議でも現代数学を破壊するので、認められない等の意見が表明された（再生核研究所声明371（2017.6.27）ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告）。そこで、初等数学から、５００件を超えるゼロ除算の証拠、効用の事実を示して、ゼロ除算は確定していること、ゼロ除算算法の重要性を主張し、基本的な世界を示している。
ゼロ除算について、膨大な歴史、文献は、ゼロ除算が神秘的なこととして、扱われ、それはアインシュタインの言葉に象徴される：
Here, we recall Albert Einstein's words on mathematics:
Blackholes are where God divided by zero.
I don't believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} (Gamow, G., My World Line (Viking, New York). p 44, 1970).
ところが結果は、実に簡明であった：
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
しかしながら、ゼロ及びゼロ除算は、結果自体は 驚く程単純であったが、神秘的な新たな世界を覗かせ、ゼロ及びゼロ除算は一層神秘的な対象であることが顕になってきた。ゼロのいろいろな意味も分かってきた。 無限遠点における強力な飛び、ワープ現象とゼロと無限の不思議な関係である。アリストテレス、ユークリッド以来の 空間の認識を変える事件をもたらしている。 ゼロ除算の結果は、数理論ばかりではなく、世界観の変更を要求している。 端的に表現してみよう。 これは宇宙の生成、消滅の様、人生の様をも表しているようである。 点が球としてどんどん大きくなり、球面は限りなく大きくなって行く。 どこまで大きくなっていくかは、 分からない。しかしながら、ゼロ除算はあるところで突然半径はゼロになり、最初の点に帰するというのである。 ゼロから始まってゼロに帰する。 ―― それは人生の様のようではないだろうか。物心なしに始まった人生、経験や知識はどんどん広がって行くが、突然、死によって元に戻る。 人生とはそのようなものではないだろうか。 はじめも終わりも、 途中も分からない。 多くの世の現象はそのようで、 何かが始まり、 どんどん進み、そして、戻る。 例えばソロバンでは、願いましては で計算を始め、最後はご破産で願いましては、で終了する。 我々の宇宙も淀みに浮かぶ泡沫のようなもので、できては壊れ、できては壊れる現象を繰り返しているのではないだろうか。泡沫の上の小さな存在の人間は結局、何も分からず、われ思うゆえにわれあり と自己の存在を確かめる程の能力しか無い存在であると言える。 始めと終わり、過程も ようとして分からない。
ブラックホールとゼロ除算、ゼロ除算の発見とその後の数学の発展を眺めていて、そのような宇宙観、人生観がひとりでに湧いてきて、奇妙に納得のいく気持ちになっている。
以 上
0 件のコメント:
コメントを投稿