God Old Boy

This interview explores God's ability to do the impossible, like divide by zero or add two plus two and get five. The final panel is meant to show a creative solution to a seemingly impossible problem by creating a sort of non-Euclidean shape that is both square and triangle. The question still remains though, could God divide by zero? tune in next week! (no, not really)
とても興味深く読みました:
再生核研究所声明353(2017.2.2) ゼロ除算 記念日
2014.2.2 に 一般の方から100/0 の意味を問われていた頃、偶然に執筆中の論文原稿にそれがゼロとなっているのを発見した。直ぐに結果に驚いて友人にメールしたり、同僚に話した。それ以来、ちょうど3年、相当詳しい記録と経過が記録されている。重要なものは再生核研究所声明として英文と和文で公表されている。最初のものは
再生核研究所声明 148(2014.2.12): 100/0=0, 0/0=0 - 割り算の考えを自然に拡張すると ― 神の意志
で、最新のは
Announcement 352 (2017.2.2): On the third birthday of the division by zero z/0=0
である。
アリストテレス、ブラーマグプタ、ニュートン、オイラー、アインシュタインなどが深く関与する ゼロ除算の神秘的な永い歴史上の発見であるから、その日をゼロ除算記念日として定めて、世界史を進化させる決意の日としたい。ゼロ除算は、ユークリッド幾何学の変更といわゆるリーマン球面の無限遠点の考え方の変更を求めている。― 実際、ゼロ除算の歴史は人類の闘争の歴史と共に 人類の愚かさの象徴であるとしている。
心すべき要点を纏めて置きたい。
1) ゼロの明確な発見と算術の確立者Brahmagupta (598 - 668 ?) は 既にそこで、0/0=0 と定義していたにも関わらず、言わば創業者の深い考察を理解できず、それは間違いであるとして、1300年以上も間違いを繰り返してきた。
2) 予断と偏見、慣習、習慣、思い込み、権威に盲従する人間の精神の弱さ、愚かさを自戒したい。我々は何時もそのように囚われていて、虚像を見ていると 真智を愛する心を大事にして行きたい。絶えず、それは真かと 問うていかなければならない。
3) ピタゴラス派では 無理数の発見をしていたが、なんと、無理数の存在は自分たちの世界観に合わないからという理由で、― その発見は都合が悪いので ― 、弟子を処刑にしてしまったという。真智への愛より、面子、権力争い、勢力争い、利害が大事という人間の浅ましさの典型的な例である。
4) この辺は、2000年以上も前に、既に世の聖人、賢人が諭されてきたのに いまだ人間は生物の本能レベルを越えておらず、愚かな世界史を続けている。人間が人間として生きる意義は 真智への愛にある と言える。
5) いわば創業者の偉大な精神が正確に、上手く伝えられず、ピタゴラス派のような対応をとっているのは、本末転倒で、そのようなことが世に溢れていると警戒していきたい。本来あるべきものが逆になっていて、社会をおかしくしている。
6) ゼロ除算の発見記念日に 繰り返し、人類の愚かさを反省して、明るい世界史を切り拓いて行きたい。
以 上
追記:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告
http://ameblo.jp/syoshinoris/theme-10006253398.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html
再生核研究所声明 382 (2017.9.11): ニュートンを越える天才たちに-育成する立場の人に
次のような文書を残した: いま思いついたこと:ニュートンは偉く、ガウス、オイラーなども 遥かに及ばないと 何かに書いてあると言うのです。それで、考え、思いついた。 ガウス、オイラーの業績は とても想像も出来なく、如何に基本的で、深く、いろいろな結果がどうして得られたのか、思いもよらない。まさに天才である。数学界にはそのような天才が、結構多いと言える。しかるに、ニュートンの業績は 万有引力の法則、運動の法則、微積分学さえ、理解は常人でも出来き、多くの数学上の結果もそうである。しかるにその偉大さは 比べることも出来ない程であると表現されると言う。それは、どうしてであろうか。確かに世界への甚大な影響として 納得できる面がある。- 初めて スタンフォード大学を訪れた時、確かにニュートンの肖像画が 別格高く掲げられていたことが、鮮明に想い出されてくる。- 今でもそうであろうか?(2017.9.8.10:42)。
万物の運動を支配する法則、力、エネルギーの原理、長さ、面積、体積を捉え、傾き、勾配等の概念を捉えたのであるから、森羅万象のある基礎部分をとらえたものとして、世界史における影響が甚大であると考えれば その業績の大きさに驚かされる。
世界史における甚大な影響として、科学上ではないが、それらを越える、宗教家の大きな存在に まず、注意を喚起して置きたい。数学者、天文学者では ゼロを数として明確に導入し、負の数も考え、算術の法則(四則演算)を確立し、ゼロ除算0/0=0を宣言したBrahmagupta (598 -668 ?) の 偉大な影響 にも特に注意したい。
そのように偉大なるニュートンを発想すれば、それを越える偉大なる歴史上の存在の可能性を考えたくなるのは人情であろう。そこで、天才たちやそれを育成したいと考える人たちに 如何に考えるべきかを述べて置きたい。
万人にとって近い存在で、甚大な貢献をするであろう、科学的な分野への志向である。鍵は 生命と情報ではないだろうか。偉大なる発見、貢献であるから具体的に言及できるはずがない。しかしながら、科学が未だ十分に達しておらず、しかも万人に甚大な影響を与える科学の未知の分野として、生命と情報分野における飛躍的な発見は ニュートンを越える発見に繋がるのではないだろうか。
生物とは何者か、どのように作られ、どのように活動しているか、本能と環境への対応の原理を支配する科学的な体系、説明である。生命の誕生と終末の後、人間精神の在り様と物理的な世界の関係、殆ど未知の雄大な分野である。
情報とは何か、情報と人間の関係、影響、発展する人工知能の方向性とそれらを統一する原理と理論。情報と物の関係。情報が物を動かしている実例が存在する。
それらの分野における画期的な成果は ニュートンを越える世界史上の発見として出現するのではないだろうか。
これらの難解な課題においてニュ-トンの場合の様に常人でも理解できるような簡明な法則が発見されるのではないだろうか。
人類未だ猿や動物にも劣る存在であるとして、世界史を恥ずかしい歴史として、未来人は考え、評価するだろう。世の天才たちの志向について、またそのような偉大なる人材を育成する立場の方々の注意を喚起させたい。偉大なる楽しい夢である。
それにはまずは、世界史を視野に、人間とは何者かと問い、神の意思を捉えようとする真智への愛を大事に育てて行こうではないか。
以 上
再生核研究所声明 375 (2017.7.21):ブラックホール、ゼロ除算、宇宙論
本年はブラックホール命名50周年とされていたが、最近、wikipedia で下記のように修正されていた:
名称[編集]
"black hole"という呼び名が定着するまでは、崩壊した星を意味する"collapsar"[1](コラプサー)などと呼ばれていた。光すら脱け出せない縮退星に対して "black hole" という言葉が用いられた最も古い印刷物は、ジャーナリストのアン・ユーイング (Ann Ewing) が1964年1月18日の Science News-Letter の "'Black holes' in space" と題するアメリカ科学振興協会の会合を紹介する記事の中で用いたものである[2][3][4]。一般には、アメリカの物理学者ジョン・ホイーラーが1967年に "black hole" という名称を初めて用いたとされるが[5]、実際にはその年にニューヨークで行われた会議中で聴衆の一人が洩らした言葉をホイーラーが採用して広めたものであり[3]、またホイーラー自身は "black hole" という言葉の考案者であると主張したことはない[3]。https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%A9%E3%83%83%E3%82%AF%E3%83%9B%E3%83%BC%E3%83%AB
世界は広いから、情報が混乱することは よく起きる状況がある。ブラックホールの概念と密接な関係のあるゼロ除算の発見(2014.2.2)については、歴史的な混乱が生じないようにと 詳しい経緯、解説、論文、公表過程など記録するように配慮してきた。
ゼロ除算は簡単で自明であると初期から述べてきたが、問題はそこから生じるゼロ除算算法とその応用であると述べている。しかし、その第1歩で議論は様々でゼロ除算自身についていろいろな説が存在して、ゼロ除算は現在も全体的に混乱していると言える。インターネットなどで参照出来る膨大な情報は、我々の観点では不適当なものばかりであると言える。もちろん学術界ではゼロ除算発見後3年を経過しているものの、古い固定観念に囚われていて、新しい発見は未だ認知されているとは言えない。最近国際会議でも現代数学を破壊するので、認められない等の意見が表明された(再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告)。そこで、初等数学から、500件を超えるゼロ除算の証拠、効用の事実を示して、ゼロ除算は確定していること、ゼロ除算算法の重要性を主張し、基本的な世界を示している。
ゼロ除算について、膨大な歴史、文献は、ゼロ除算が神秘的なこととして、扱われ、それはアインシュタインの言葉に象徴される:
Here, we recall Albert Einstein's words on mathematics:
Blackholes are where God divided by zero.
I don't believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} (Gamow, G., My World Line (Viking, New York). p 44, 1970).
ところが結果は、実に簡明であった:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
しかしながら、ゼロ及びゼロ除算は、結果自体は 驚く程単純であったが、神秘的な新たな世界を覗かせ、ゼロ及びゼロ除算は一層神秘的な対象であることが顕になってきた。ゼロのいろいろな意味も分かってきた。 無限遠点における強力な飛び、ワープ現象とゼロと無限の不思議な関係である。アリストテレス、ユークリッド以来の 空間の認識を変える事件をもたらしている。 ゼロ除算の結果は、数理論ばかりではなく、世界観の変更を要求している。 端的に表現してみよう。 これは宇宙の生成、消滅の様、人生の様をも表しているようである。 点が球としてどんどん大きくなり、球面は限りなく大きくなって行く。 どこまで大きくなっていくかは、 分からない。しかしながら、ゼロ除算はあるところで突然半径はゼロになり、最初の点に帰するというのである。 ゼロから始まってゼロに帰する。 ―― それは人生の様のようではないだろうか。物心なしに始まった人生、経験や知識はどんどん広がって行くが、突然、死によって元に戻る。 人生とはそのようなものではないだろうか。 はじめも終わりも、 途中も分からない。 多くの世の現象はそのようで、 何かが始まり、 どんどん進み、そして、戻る。 例えばソロバンでは、願いましては で計算を始め、最後はご破産で願いましては、で終了する。 我々の宇宙も淀みに浮かぶ泡沫のようなもので、できては壊れ、できては壊れる現象を繰り返しているのではないだろうか。泡沫の上の小さな存在の人間は結局、何も分からず、われ思うゆえにわれあり と自己の存在を確かめる程の能力しか無い存在であると言える。 始めと終わり、過程も ようとして分からない。
ブラックホールとゼロ除算、ゼロ除算の発見とその後の数学の発展を眺めていて、そのような宇宙観、人生観がひとりでに湧いてきて、奇妙に納得のいく気持ちになっている。
以 上
再生核研究所声明 383 (2017.9.18): 人間の精神の高まりについての視点
題名の正確な意味の表現は難しい。そこで、具体的な例を挙げて意図していることをより明らかにしよう。
小学生時代を回想しよう。 低学年ではどんどん世界が広がっていくようで、知識も情報も世界も段々、どんどん広がりどんどん世界が見えるようになっていくと感じられるだろう。 それと同時に 過去の自分の様、様子が良く見える、分かる様に感じられるだろう。 このような現象は、登山でどんどん登って行くと視野が開けて、辿ってきた様、情景がすっかり見え全体の様子が分かるような経験にもみられる。このような事は旅行で ある小さな町を訪れ、滞在しているにつれて 町全体の様子が段々分かってきて、町全体をあるイメージで捉えられるようになるだろう。最初の段階で戸惑っていた自分を知ることが出来るだろう。これらの現象は様様の研究や学問、芸術、修業等についてもみられるといえる。― ある意味での進化である。 ここでは、そのような現象を、登山の例から 人間精神の高まりと表現した。正確な表現は心の問題であるから難しい。大きな特徴は段々今までの状況を含むような形で、知識や情報が拡大して、心も質的に変化して以前の状況をより広い視点から捉えられるように成長、進んでいることである。
人生とは何か、人間とは何かの基本的な 方向として、この意味における人間の精神の高まりがあると考えられる。逆に考えてみれば、知識や情報が拡大し、精神の高まりがなければ、必ず、停滞、退屈になり、そのような生活には飽きて、生き生きした人生にはならないのではないだろうか。人間、生物的な 本能的な欲求がある程度満たされれば、必ず、情報や知識を欲求し、やがて神の意思を知りたいという真智への愛に至るのではないだろうか。 この過程にみられる、人間の精神の高まり の様子、 状況に関心を持つ。
人間は真理を追究し、情報、知識の増大方向で進むが どんどん山頂を目指して進む時、 我々の精神全体はどのように変化していくであろうか、人間とはどのように成長していくであろうか。 数学界の天才、ニュートンとライプニッツは 生涯微積分学の発見の先駆者たるを主張して、裁判闘争を続けていたという、お粗末とも言える、事実が存在する。他方、精神の高まりを象徴する用語として、人物たる人物、人格者、覚者、賢人、悟りの境地、聖人などの理想を表す概念が存在する。― 人類自身、全体があたかも子供たちである様に見えてしまう進化した人間を想定すると慄然とするだろう。人生、世界、人類さえみえてしまう者の存在、思い当たる人として お釈迦様などが考えられよう。
ゼロ除算の発見で、人生とはゼロから始まり、何かが拡大を続け、やがて突然にゼロに帰すると表現した。この拡大は 正確には何を意味するであろうか。知識や情報、経験の増大は基本的であるが、覚性度なども気になる要素ではないだろうか。どんどん気づき、世界がどんどん見えてくる面である。
人生、精神的な高まりを通して成人を迎え、円熟期を迎えるが、人間の成長の理想的な境地とは何であろうか。知識を沢山集めてものしりになったり、どんどん発見や発明を続けていけば良いのだろうか。沢山良いものを発見したり、発明していけば良いのだろうか。
人間とは どのように作られているのかと 問う。― 人間存在の意義を求めている。
ある山頂に達して、人生、世界とは そのようなものであるとの見識に達した時、その心情のいろいろな在り様と いろいろな差は どのように解釈されるべきであろうか?
良き、人間とは、人生とはどのようなものであろうか?
― しかしながら、人生における基本定理、 人生の意義は感動することにある はそのような思考の基本になるのではないだろうか。
以 上
再生核研究所声明312(2016.07.14) ゼロ除算による 平成の数学改革を提案する
アリストテレス以来、あるいは西暦628年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題 ゼロ除算は、本質的に新しい局面を迎え、数学における基礎的な部分の欠落が明瞭になってきた。ここ70年を越えても教科書や学術書における数学の基礎的な部分の変更は かつて無かった事である。
そこで、最近の成果を基に現状における学術書、教科書の変更すべき大勢を外観して置きたい。特に、大学学部までの初等数学において、日本人の寄与は皆無であると言えるから、日本人が数学の基礎に貢献できる稀なる好機にもなるので、数学者、教育者など関係者の注意を換気したい。― この文脈では稀なる日本人数学者 関孝和の業績が世界の数学に活かせなかったことは 誠に残念に思われる。
先ず、数学の基礎である四則演算において ゼロでは割れない との世の定説を改め、自然に拡張された分数、割り算で、いつでも四則演算は例外なく、可能であるとする。山田体の導入。その際、小学生から割り算や分数の定義を除算の意味で 繰り返し減法(道脇方式)で定義し、ゼロ除算は自明であるとし 計算機が割り算を行うような算法で 計算方法も指導する。― この方法は割り算の簡明な算法として児童に歓迎されるだろう。
反比例の法則や関数y=1/xの出現の際には、その原点での値はゼロであると 定義する。その広範な応用は 学習過程の進展に従って どんどん触れて行くこととする。
いわゆるユークリッド幾何学の学習においては、立体射影の概念に早期に触れ、ゼロ除算が拓いた新しい空間像を指導する。無限、無限の彼方の概念、平行線の概念、勾配の概念を変える必要がある。どのように、如何に、カリキュラムに取り組むかは、もちろん、慎重な検討が必要で、数学界、教育界などの関係者による国家的取り組み、協議が必要である。重要項目は、直角座標系で y軸の勾配はゼロであること。真無限における破壊現象、接線などの新しい性質、解析幾何学との美しい関係と調和。すべての直線が原点を代数的に通り、平行な2直線は原点で代数的に交わっていること。行列式と破壊現象の美しい関係など。
大学レベルになれば、微積分、線形代数、微分方程式、複素解析をゼロ除算の成果で修正、補充して行く。複素解析学におけるローラン展開の学習以前でも形式的なローラン展開(負べき項を含む展開)の中心の値をゼロ除算で定義し、広範な応用を展開する。特に微分係数が正や負の無限大の時、微分係数をゼロと修正することによって、微分法の多くの公式や定理の表現が簡素化され、教科書の結構な記述の変更が要求される。媒介変数を含む多くの関数族は、ゼロ除算 算法で統一的な視点が与えられる。多くの公式の記述が簡単になり、修正される。
複素解析学においては 無限遠点はゼロで表現されると、コペルニクス的変更(無限とされていたのが実はゼロだった)を行い、極の概念を次のように変更する。極、特異点の定義は そのままであるが、それらの点の近傍で、限りなく無限の値に近づく値を位数まで込めて取るが、特異点では、ゼロ除算に言う、有限確定値をとるとする。その有限確定値のいろいろ幾何学な意味を学ぶ。古典的な鏡像の定説;原点の 原点を中心とする円の鏡像は無限遠点であるは、誤りであり、修正し、ゼロであると いろいろな根拠によって説明する。これら、無限遠点の考えの修正は、ユークリッド以来、我々の空間に対する認識の世界史上に置ける大きな変更であり、数学を越えた世界観の変更を意味している。― この文脈では天動説が地動説に変わった歴史上の事件が想起される。
ゼロ除算は 物理学を始め、広く自然科学や計算機科学への大きな影響が期待される。しかしながら、ゼロ除算の研究成果を教科書、学術書に遅滞なく取り入れていくことは、真智への愛、真理の追究の表現であり、四則演算が自由にできないとなれば、人類の名誉にも関わることである。ゼロ除算の発見は 日本の世界に置ける顕著な貢献として世界史に記録されるだろう。研究と活用の推進を 大きな夢を懐きながら 要請したい。
以 上
追記:
(2016) Matrices and Division by Zero z/0 = 0. Advances in Linear Algebra & Matrix Theory, 6, 51-58.
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdfDOI:10.12732/ijam.v27i2.9.














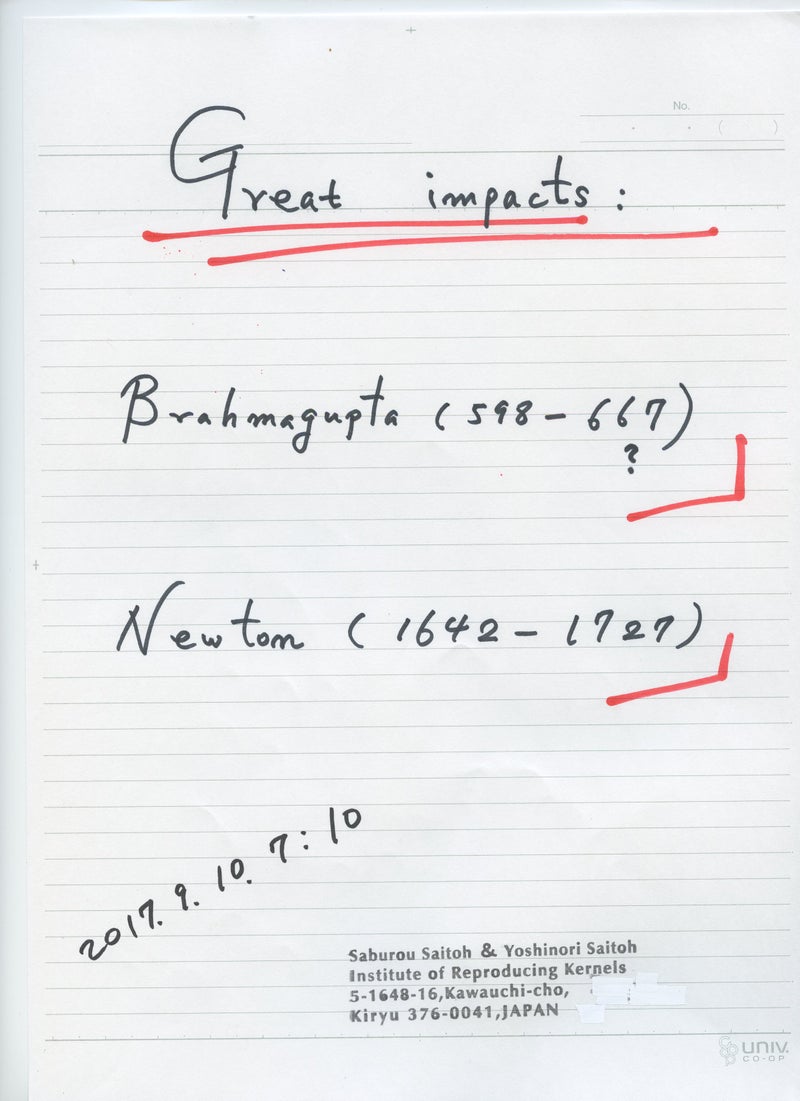














































0 件のコメント:
コメントを投稿