世界最古の「ゼロ」記号、その誕生が従来より500年も早かったことが判明
数学史が変わる。古代インドの写本を放射性炭素年代測定したところ、のちに数字のゼロに進化する記号は、これまで考えられていたより少なくとも約500年も早く出現していたことが明らかになりました。 現存する唯一の数学的な書物であるバクシャーリー写本は、これまでの研究では8世紀から12世紀にかけて作られたとされていましたが、放射性炭素年代測定でその時期は西暦224年から383年へとさかのぼることに。バクシャーリー写本には黒いドットで記されたゼロの記号がたくさん見られますが、それこそがのちに数字へと進化する記号の最古の使用例となっているのです。バクシャーリー写本は、1881年にバクシャーリー村(現パキスタン)近くの野原に埋められているところを、地元の農家が発見。1902年にオックスフォード大学のボドリアン図書館へ送られて以降、ずっと保管されています。以前の分析では、テキストの言語が仏教混淆サンスクリットだと特定。写本には何百ものゼロの記号が含まれており、日々の商いのために参照する必要のあった商人たちが使っていた可能性があります。しかし原稿の正確な執筆時期はハッキリとわからないままでした。そこで2017年初頭、写本を放射性炭素年代測定するプロジェクトをついにオックスフォード大学のボドリアン図書館と放射性炭素年代測定ユニットの研究者たちが共同で行なうことになったのです。
Image: Bodleian Libraries, University of Oxford
放射性炭素年代測定によってバクシャーリー写本は西暦224年から383年にさかのぼるとされ、位取り記数法において大きさを示すためにゼロをプレースホルダーとして使っていた最も初期の例(ドットとして記載されている)になります。
以前の調査では、バクシャーリー写本の制作時期は8世紀から12世紀の間に執筆されたものだとされていましたが、その分析は文体や文語と数学的な内容やその他の要因に基づくものでした。しかし、最新技術の放射性炭素年代測定によって、作られた時代をはっきりさせるのが困難だった理由が明らかになったのです。というのも、写本は70ページに及び、樺製で壊れやすく、少なくとも3つの異なる時代の素材からできていたことがわかりました。しかしこの分析はまだ査読も、科学誌での発表もされていません。「これについては論文として言及しているものの、ジャーナル/出版物にはまだ提出されていません」とボドリアン図書館のスポークスマンは説明しました。「私たちは執筆者たちに放射性炭素年代測定によるリサーチの結果をもっと細かくみてもられるように、この論文を提供しています」とのこと 。
Image: Bodleian Libraries, University of Oxford
バクシャーリー写本を構成する70枚の樺の樹皮はとても繊細で、この特別にデザインされた本に格納されています。研究者は本の「窓」を通してページの両面を見ることできます
ゼロの概念は直覚的なもののように思えますが、それは私たちが既に慣れ親しんでいるからです。「この木にはリンゴがない」と「この木にはリンゴがゼロ個である」と言うのでは、概念的に大きな飛躍があります。歴史的に見て、「何もない」を表すためのプレースホルダーを求める概念は、古代マヤやバビロニアの社会などを含む複数の異なる古代文化で出現しました。しかし、バクシャーリー写本におけるゼロの使用は2つの理由によって重要なのです。1つめの理由は、バクシャーリー写本に現れる黒いドットが今では数字のゼロを表す真ん中が空洞の円へとのちに進化したこと。2点目は、それがのちに数字へと変化する、現存する唯一のゼロのプレースホルダーだからです。論文に添えられた考察でオックスフォード大学の数学教授マーカス・デュ・ソートイ氏は、以下のようにそれを説明しています。
Image: Bodleian Libraries, University of Oxford
放射性炭素年代測定によってバクシャーリー写本は西暦224年から383年にさかのぼるとされ、位取り記数法において大きさを示すためにゼロをプレースホルダーとして使っていた最も初期の例(ドットとして記載されている)になります。
以前の調査では、バクシャーリー写本の制作時期は8世紀から12世紀の間に執筆されたものだとされていましたが、その分析は文体や文語と数学的な内容やその他の要因に基づくものでした。しかし、最新技術の放射性炭素年代測定によって、作られた時代をはっきりさせるのが困難だった理由が明らかになったのです。というのも、写本は70ページに及び、樺製で壊れやすく、少なくとも3つの異なる時代の素材からできていたことがわかりました。しかしこの分析はまだ査読も、科学誌での発表もされていません。「これについては論文として言及しているものの、ジャーナル/出版物にはまだ提出されていません」とボドリアン図書館のスポークスマンは説明しました。「私たちは執筆者たちに放射性炭素年代測定によるリサーチの結果をもっと細かくみてもられるように、この論文を提供しています」とのこと 。
Image: Bodleian Libraries, University of Oxford
バクシャーリー写本を構成する70枚の樺の樹皮はとても繊細で、この特別にデザインされた本に格納されています。研究者は本の「窓」を通してページの両面を見ることできます
ゼロの概念は直覚的なもののように思えますが、それは私たちが既に慣れ親しんでいるからです。「この木にはリンゴがない」と「この木にはリンゴがゼロ個である」と言うのでは、概念的に大きな飛躍があります。歴史的に見て、「何もない」を表すためのプレースホルダーを求める概念は、古代マヤやバビロニアの社会などを含む複数の異なる古代文化で出現しました。しかし、バクシャーリー写本におけるゼロの使用は2つの理由によって重要なのです。1つめの理由は、バクシャーリー写本に現れる黒いドットが今では数字のゼロを表す真ん中が空洞の円へとのちに進化したこと。2点目は、それがのちに数字へと変化する、現存する唯一のゼロのプレースホルダーだからです。論文に添えられた考察でオックスフォード大学の数学教授マーカス・デュ・ソートイ氏は、以下のようにそれを説明しています。
バクシャーリー写本で使われているゼロは、まだそれ自体が数字ではありません。位取り記数法で書かれた他の数字の一部として使われるプレースホルダーなのです。我々は101と書いて、100と10の位はなく1のユニットだと示しています。この0は10の位がないことを示しているのです。位取り記数法で数字を書く一環として、無を表す記号を必要とするというアイデアは、とても古い伝統を持っています。5000年前、バビロニア人たちは石板に数字を書くために、楔形文字の一部として何もない二重くさびを使っていました。2000年前、マヤ人たちは彼らの数系で、不在を示すのに貝のシンボルを使っていたのです。そのため、バクシャーリー写本で使われていた黒いドットは、より大きな数字を組み立てる方法としてのゼロを使った最初の例ではないものの、ゼロの概念が自ずから現れるための種となったとデュ・ソートイ教授は語っています。「バクシャーリー写本の年代を測定することは、数学史において極めて重要です。初期の南アジア文化の研究とこういった驚くべき研究結果は、亜大陸の豊かで長年にわたる科学的な伝統の証拠となります」とボドリアン図書館のリチャード・オーブンデン氏は、プレスリリースで語っています。オーブンデン氏いわく、この写本についての研究は完璧からは程遠いとのことですが、制作時期が分かった今、写本の元々の構造を再構成して、原文の異なる層についてより深く理解できるようになる可能性がありそうです。Image: Bodleian Libraries, University of OxfordSource: Bodleian Libraries, University of Oxford, WikipediaGeorge Dvorsky - Gizmodo US[原文](たもり) http://top.tsite.jp/news/technology/o/25374829/?sc_int=tcore_news_recent
とても興味深く読みました:
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 380: What is the zero?\\
(2017.8.21)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
}
\date{\today}
\maketitle
\section{What is the zero?}
The zero $0$ as the complex number or real number is given clearly by the axions by the complex number field and real number field.
For this fundamental idea, we should consider the {\bf Yamada field} containing the division by zero. The Yamada field and the division by zero calculus will arrange our mathematics, beautifully and completely; this will be our natural and complete mathematics.
\medskip
\section{ Double natures of the zero $z=0$}
The zero point $z=0$ represents the double natures; one is the origin at the starting point and another one is a representation of the point at infinity. One typical and simple example is given by $e^0 = 1,0$, two values. {\bf God loves two}.
\section{Standard value}
\medskip
The zero is a center and stand point (or bases, a standard value) of the coordinates - here we will consider our situation on the complex or real 2 dimensional spaces. By stereographic
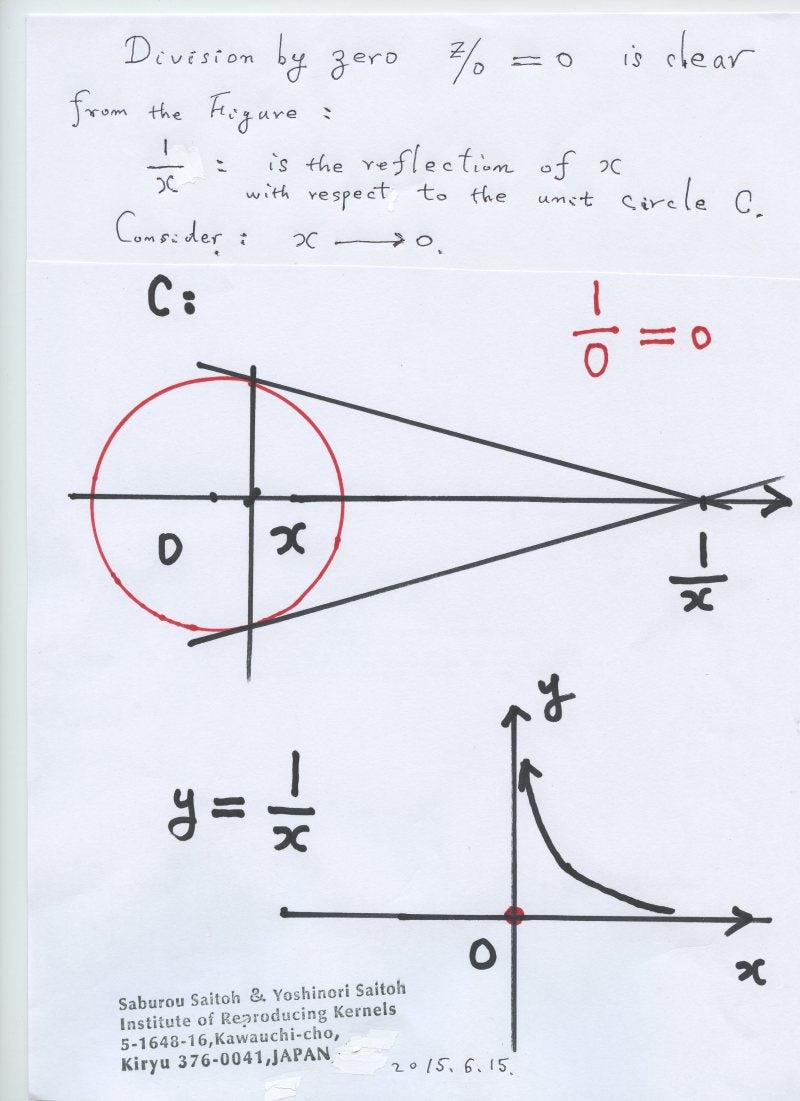
projection mapping or the Yamada field, the point at infinity $1/0$ is represented by zero. The origin of the coordinates and the point at infinity correspond each other.
As the standard value, for the point $\omega_n = \exp \left(\frac{\pi}{n}i\right)$ on the unit circle $|z|=1$ on the complex $z$-plane is, for $n = 0$:
\begin{equation}
\omega_0 = \exp \left(\frac{\pi}{0}i\right)=1, \quad \frac{\pi}{0} =0.
\end{equation}
For the mean value
$$
M_n = \frac{x_1 + x_2 +... + x_n}{n},
$$
we have
$$
M_0 = 0 = \frac{0}{0}.
$$
\medskip
\section{ Fruitful world}
\medskip
For example, for very and very general partial differential equations, if the coefficients or terms are zero, then we have some simple differential equations and the extreme case is all the terms are zero; that is, we have trivial equations $0=0$; then its solution is zero. When we consider the converse, we see that the zero world is a fruitful one and it means some vanishing world. Recall Yamane phenomena (\cite{kmsy}), the vanishing result is very simple zero, however, it is the result from some fruitful world. Sometimes, zero means void or nothing world, however, it will show {\bf some changes} as in the Yamane phenomena.
\section{From $0$ to $0$; $0$ means all and all are $0$}
\medskip
As we see from our life figure (\cite{osm}), a story starts from the zero and ends with the zero. This will mean that $0$ means all and all are $0$. The zero is a {\bf mother} or an {\bf origin} of all.
\medskip
\section{ Impossibility}
\medskip
As the solution of the simplest equation
\begin{equation}
ax =b
\end{equation}
we have $x=0$ for $a=0, b\ne 0$ as the standard value, or the Moore-Penrose generalized inverse. This will mean in a sense, the solution does not exist; to solve the equation (6.1) is impossible.
We saw for different parallel lines or different parallel planes, their common points are the origin. Certainly they have the common points of the point at infinity and the point at infinity is represented by zero. However, we can understand also that they have no solutions, no common points, because the point at infinity is an ideal point.
Of course. we can consider the equation (6.1) even the case $a=b=0$ and then we have the solution $x=0$ as we stated.
We will consider the simple differential equation
\begin{equation}
m\frac{d^2x}{dt^2} =0, m\frac{d^2y}{dt^2} =-mg
\end{equation}
with the initial conditions, at $t =0$
\begin{equation}
\frac{dx}{dt} = v_0 \cos \alpha , \frac{d^2x}{dt^2} = \frac{d^2y}{dt^2}=0.
\end{equation}
Then, the highest high $h$, arriving time $t$, the distance $d$ from the starting point at the origin to the point $y(2t) =0$ are given by
\begin{equation}
h = \frac{v_0 \sin^2 \alpha}{2g}, d= \frac{v_0\sin \alpha}{g}
\end{equation}
and
\begin{equation}
t= \frac{v_0 \sin \alpha}{g}.
\end{equation}
For the case $g=0$, we have $h=d =t=0$. We considered the case that they are the infinity; however, our mathematics means zero, which shows impossibility.
These phenomena were looked many cases on the universe; it seems that {\bf God does not like the infinity}.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msy}
H. Michiwaki, S. Saitoh, and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{ms}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$, Advances in Linear Algebra
\& Matrix Theory, 6 (2016), 51-58. http://dx.doi.org/10.4236/alamt.2016.62007 http://www.scirp.org/journal/alamt
\bibitem{mos}
H. Michiwaki, H. Okumura, and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces.
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), 1(2017), 70-77.
\bibitem{romig}
H. G. Romig, Discussions: Early History of Division by Zero,
American Mathematical Monthly, Vol. 31, No. 8. (Oct., 1924), pp. 387-389.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182 (Springer).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\bibitem{ann179}
Announcement 179 (2014.8.30): Division by zero is clear as z/0=0 and it is fundamental in mathematics.
\bibitem{ann185}
Announcement 185 (2014.10.22): The importance of the division by zero $z/0=0$.
\bibitem{ann237}
Announcement 237 (2015.6.18): A reality of the division by zero $z/0=0$ by geometrical optics.
\bibitem{ann246}
Announcement 246 (2015.9.17): An interpretation of the division by zero $1/0=0$ by the gradients of lines.
\bibitem{ann247}
Announcement 247 (2015.9.22): The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$.
\bibitem{ann250}
Announcement 250 (2015.10.20): What are numbers? - the Yamada field containing the division by zero $z/0=0$.
\bibitem{ann252}
Announcement 252 (2015.11.1): Circles and
curvature - an interpretation by Mr.
Hiroshi Michiwaki of the division by
zero $r/0 = 0$.
\bibitem{ann281}
Announcement 281 (2016.2.1): The importance of the division by zero $z/0=0$.
\bibitem{ann282}
Announcement 282 (2016.2.2): The Division by Zero $z/0=0$ on the Second Birthday.
\bibitem{ann293}
Announcement 293 (2016.3.27): Parallel lines on the Euclidean plane from the viewpoint of division by zero 1/0=0.
\bibitem{ann300}
Announcement 300 (2016.05.22): New challenges on the division by zero z/0=0.
\bibitem{ann326}
Announcement 326 (2016.10.17): The division by zero z/0=0 - its impact to human beings through education and research.
\bibitem{ann352}
Announcement 352(2017.2.2): On the third birthday of the division by zero z/0=0.
\bibitem{ann354}
Announcement 354(2017.2.8): What are $n = 2,1,0$ regular polygons inscribed in a disc? -- relations of $0$ and infinity.
\bibitem{362}
Announcement 362(2017.5.5): Discovery of the division by zero as
$0/0=1/0=z/0=0$.
\end{thebibliography}
\end{document}
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1
-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi
http://okmr.yamatoblog.net/
Relations of 0 and infinity
Hiroshi Okumura, Saburou Saitoh and Tsutomu Matsuura:
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…
https://sites.google.com/site/sandrapinelas/icddea-2017
2017.8.21.06:37







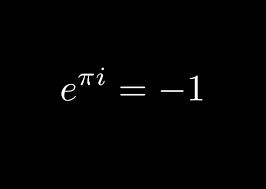





































































0 件のコメント:
コメントを投稿