شناسائی قدیمی ترین سند مکتوب استفاده از صفر؛
پیشنه عدد صفر پانصد سال به عقب بازگشت

مطالعات جدید پژوهشگران دانشگاه آکسفورد نشان می دهد قدیمی ترین سند مکتوب که در آن از عدد صفر استفاده شده است متعلق به کتابی هندی به نام باکشالی است که در حدود سال ۲۲۴ میلادی نوشته شده است.
سرپوش علمی - عدد صفر امروزه دارای کاربری های فراوانی است و نقش مهمی در ریاضیات و آمار دارد اما در حقیقت این عدد بسیار مهم دارای پیشینه ای بسیار طولانی است. مطالعات جدید باستان شناسان در پی انجام آزمایش های کربن ۱۴ انجام شده روی برخی متون قدیمی، باید تاریخ علم ریاضیات را از نو نوشت زیرا این مطالعات نشان می دهد تاریخ کشف عدد صفر حدود پانصد سال پیشتر از آن چه تا کنون تصور می شد بوده است.
استفاده از عدد صفر به عنوان نشانگر در بسیاری از تمدن های باستانی همچون تمدن مایا ها در آمریکای جنوبی و تمدن بابل در میانرودان دیده می شود اما در بین این تمدن ها تنها در هندوستان بود که عدد صفر رفته رفته جایگاه خود را یافته و برای نخستین بار در سال ۶۲۸ میلادی توسط برهماگوپتا (Brahmagupta) ریاضیدان هند باستان تشریح شد.
این سند شامل کتابی از اعداد است که از هند باستان باقی مانده و با نام باکشالی (Bakhshali) شهرت دارد. این کتاب بر هفتاد صفحه برگ درخت غان به سانسکریت نوشته شده است. مارکوس دو ساتوی (Marcus du Sautoy) از پژوهشگران این تیم تحقیقاتی در دانشگاه آکسفورد درباره این متن باستانی اعلام کرد: «به نظر می رسد این متن، یک دفترچه تمرین ریاضیات توسط کاهنان بودائی محسوب می شود.»
این متن در سال ۱۸۸۱ توسط یک کشاورز کشف شده و به نام دهکده ای که در آن قرار داشت، نامگذاری شد. این روستا امروزه در کشور پاکستان قرار داشته و کتاب فوق الذکر از سال ۱۹۰۲ میلادی تا امروز در مالکیت دانشگاه آکسفورد قرار دارد.
این متن تاریخی به تازگی تحت آزمایش های تاریخگذاری کربن قرار گرفته و برخی از اعتقادات پیشین را تغییر داد. پیش از این پژوهشگران اعتقاد داشتند که این سند به قرن نهم میلادی تعلق دارد اما آزمایش های جدید انجام شده نشان داد که قدیمی ترین صفحه این دستنوشته به دوره زمانی بین سال ۲۲۴ تا ۳۸۳ میلادی تعلق دارد.
این مطالعات نشان می دهد که در حقیقت قدیمی ترین سند مکتوبی که در آن از عدد صفر استفاده شده کتاب باکشالی بوده و عدد صفر نگاشته شده روی دیواره معبد گووالیور (Gwalior) که مربوط به قرن نهم میلادی است از این سند جدیدتر محسوب می شود.
پیش از این دیوارنگاره معبد فوق قدیمی ترین سند مربوط به استفاده و کاربرد عدد صفر به شمار می رفت. در این متن صدها بار از عدد صفر استفاده شده و این عدد به شکل نقطه نمایش داده می شود. این نماد به کار رفته برای عدد صفر در ابتدا به صورت نقطه ای تو پر بوده که به تدریج برای تمایز بین آن و نقطه از یک حفره در وسط آن استفاده شده و در نهایت به شکل عدد صفر امروزی در آمد.
در این متن نقطه در اصل به عنوان نگهدارنده استفاده می شد، مانند نحوه استفاده از عدد صفر در شماره ۵۰۵ برای نشان دادن این که هیچ دهگانی در این محل وجود ندارد، اما در این دوره هنوز عدد صفر کاربرد عدد صحیح را ندارد.

استفاده از عدد صفر به عنوان نشانگر در بسیاری از تمدن های باستانی همچون تمدن مایاها در آمریکای جنوبی و تمدن بابل در میانرودان دیده می شود اما در بین این تمدن ها تنها در هندوستان بود که عدد صفر رفته رفته جایگاه خود را یافته و برای نخستین بار در سال ۶۲۸ میلادی توسط برهماگوپتا (Brahmagupta) ریاضیدان هند باستان تشریح شد.
مارکوس دو ساتوی در این رابطه می گوید: «برخی از این ایده ها برای ما ضروری بود. کاربرد اصلی اعداد برای شمارش است و وقتی شما بخواهید نشان دهید که هیچ چیزی وجود ندارد نیز به عدد نیاز خواهید داشت.»
ایده استفاده از صفر در ابتدا به عنوان یک بدعت نادرست با مخالفت رو به رو شده بود اما رفته رفته با پیشرفت علم محاسبات این عدد اهمیت بیشتری یافته و امروزه تقریبا تمامی بنیان فناوری مدرن بر اساس صفر و یک و یا وجود یا وجود نداشتن چیزی شکل گرفته است.
گفتنی است تاریخگذاری این کتابچه بسیار دشوار است زیرا بین زمان نگارش قدیمی ترین صفحات این کتاب و متاخر ترین آن ها حدود پانصد سال فاصله وجود دارد. این موضوع سبب شده است تا پژوهشگران در پی کشف این معما باشند که چگونه این صفحات از دوره های مختلف تاریخی در کنار یکدیگر جمع آوری شده و به صورت کتابچه در آمده اند؟
ترجمه: احسان محمدحسینی
とても興味深く読みました:
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 380: What is the zero?\\
(2017.8.21)}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
}
\date{\today}
\maketitle
\section{What is the zero?}
The zero $0$ as the complex number or real number is given clearly by the axions by the complex number field and real number field.
For this fundamental idea, we should consider the {\bf Yamada field} containing the division by zero. The Yamada field and the division by zero calculus will arrange our mathematics, beautifully and completely; this will be our natural and complete mathematics.
\medskip
\section{ Double natures of the zero $z=0$}
The zero point $z=0$ represents the double natures; one is the origin at the starting point and another one is a representation of the point at infinity. One typical and simple example is given by $e^0 = 1,0$, two values. {\bf God loves two}.
\section{Standard value}
\medskip
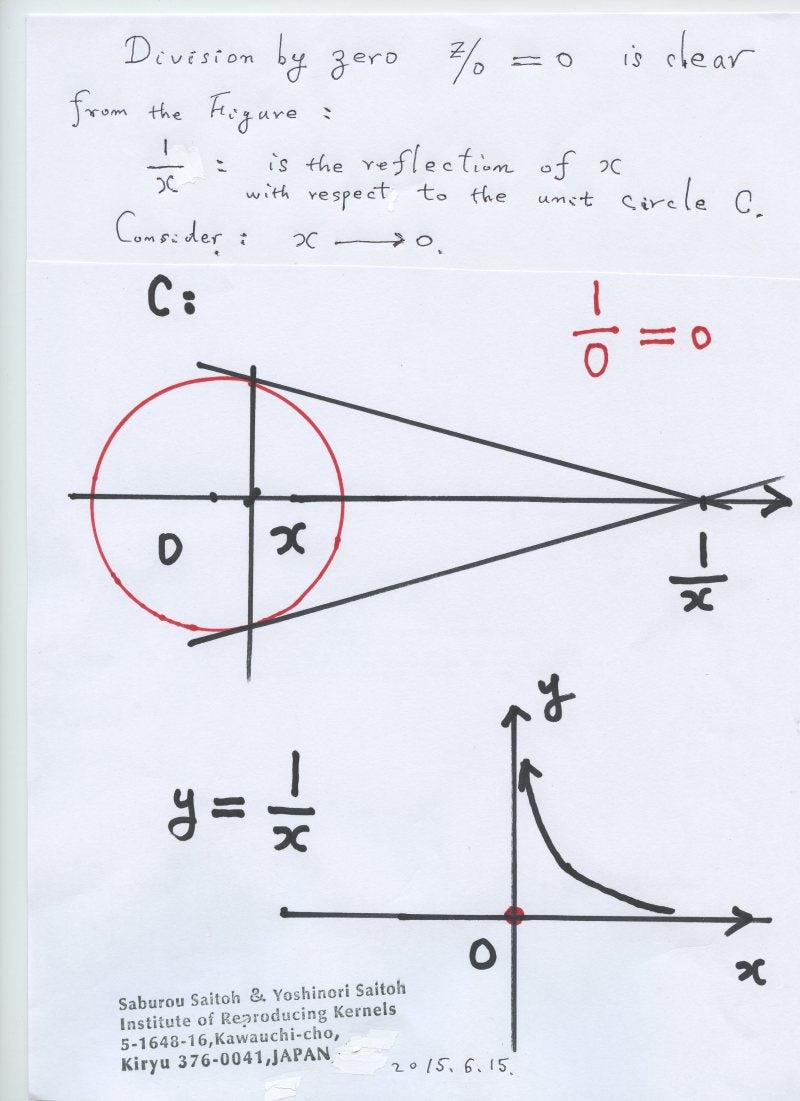
The zero is a center and stand point (or bases, a standard value) of the coordinates - here we will consider our situation on the complex or real 2 dimensional spaces. By stereographic
projection mapping or the Yamada field, the point at infinity $1/0$ is represented by zero. The origin of the coordinates and the point at infinity correspond each other.
As the standard value, for the point $\omega_n = \exp \left(\frac{\pi}{n}i\right)$ on the unit circle $|z|=1$ on the complex $z$-plane is, for $n = 0$:
\begin{equation}
\omega_0 = \exp \left(\frac{\pi}{0}i\right)=1, \quad \frac{\pi}{0} =0.
\end{equation}
For the mean value
$$
M_n = \frac{x_1 + x_2 +... + x_n}{n},
$$
we have
$$
M_0 = 0 = \frac{0}{0}.
$$
\medskip
\section{ Fruitful world}
\medskip
For example, for very and very general partial differential equations, if the coefficients or terms are zero, then we have some simple differential equations and the extreme case is all the terms are zero; that is, we have trivial equations $0=0$; then its solution is zero. When we consider the converse, we see that the zero world is a fruitful one and it means some vanishing world. Recall Yamane phenomena (\cite{kmsy}), the vanishing result is very simple zero, however, it is the result from some fruitful world. Sometimes, zero means void or nothing world, however, it will show {\bf some changes} as in the Yamane phenomena.
\section{From $0$ to $0$; $0$ means all and all are $0$}
\medskip
As we see from our life figure (\cite{osm}), a story starts from the zero and ends with the zero. This will mean that $0$ means all and all are $0$. The zero is a {\bf mother} or an {\bf origin} of all.
\medskip
\section{ Impossibility}
\medskip
As the solution of the simplest equation
\begin{equation}
ax =b
\end{equation}
we have $x=0$ for $a=0, b\ne 0$ as the standard value, or the Moore-Penrose generalized inverse. This will mean in a sense, the solution does not exist; to solve the equation (6.1) is impossible.
We saw for different parallel lines or different parallel planes, their common points are the origin. Certainly they have the common points of the point at infinity and the point at infinity is represented by zero. However, we can understand also that they have no solutions, no common points, because the point at infinity is an ideal point.
Of course. we can consider the equation (6.1) even the case $a=b=0$ and then we have the solution $x=0$ as we stated.
We will consider the simple differential equation
\begin{equation}
m\frac{d^2x}{dt^2} =0, m\frac{d^2y}{dt^2} =-mg
\end{equation}
with the initial conditions, at $t =0$
\begin{equation}
\frac{dx}{dt} = v_0 \cos \alpha , \frac{d^2x}{dt^2} = \frac{d^2y}{dt^2}=0.
\end{equation}
Then, the highest high $h$, arriving time $t$, the distance $d$ from the starting point at the origin to the point $y(2t) =0$ are given by
\begin{equation}
h = \frac{v_0 \sin^2 \alpha}{2g}, d= \frac{v_0\sin \alpha}{g}
\end{equation}
and
\begin{equation}
t= \frac{v_0 \sin \alpha}{g}.
\end{equation}
For the case $g=0$, we have $h=d =t=0$. We considered the case that they are the infinity; however, our mathematics means zero, which shows impossibility.
These phenomena were looked many cases on the universe; it seems that {\bf God does not like the infinity}.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msy}
H. Michiwaki, S. Saitoh, and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{ms}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$, Advances in Linear Algebra
\& Matrix Theory, 6 (2016), 51-58. http://dx.doi.org/10.4236/alamt.2016.62007 http://www.scirp.org/journal/alamt
\bibitem{mos}
H. Michiwaki, H. Okumura, and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces.
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), 1(2017), 70-77.
\bibitem{romig}
H. G. Romig, Discussions: Early History of Division by Zero,
American Mathematical Monthly, Vol. 31, No. 8. (Oct., 1924), pp. 387-389.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182 (Springer).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\bibitem{ann179}
Announcement 179 (2014.8.30): Division by zero is clear as z/0=0 and it is fundamental in mathematics.
\bibitem{ann185}
Announcement 185 (2014.10.22): The importance of the division by zero $z/0=0$.
\bibitem{ann237}
Announcement 237 (2015.6.18): A reality of the division by zero $z/0=0$ by geometrical optics.
\bibitem{ann246}
Announcement 246 (2015.9.17): An interpretation of the division by zero $1/0=0$ by the gradients of lines.
\bibitem{ann247}
Announcement 247 (2015.9.22): The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$.
\bibitem{ann250}
Announcement 250 (2015.10.20): What are numbers? - the Yamada field containing the division by zero $z/0=0$.
\bibitem{ann252}
Announcement 252 (2015.11.1): Circles and
curvature - an interpretation by Mr.
Hiroshi Michiwaki of the division by
zero $r/0 = 0$.
\bibitem{ann281}
Announcement 281 (2016.2.1): The importance of the division by zero $z/0=0$.
\bibitem{ann282}
Announcement 282 (2016.2.2): The Division by Zero $z/0=0$ on the Second Birthday.
\bibitem{ann293}
Announcement 293 (2016.3.27): Parallel lines on the Euclidean plane from the viewpoint of division by zero 1/0=0.
\bibitem{ann300}
Announcement 300 (2016.05.22): New challenges on the division by zero z/0=0.
\bibitem{ann326}
Announcement 326 (2016.10.17): The division by zero z/0=0 - its impact to human beings through education and research.
\bibitem{ann352}
Announcement 352(2017.2.2): On the third birthday of the division by zero z/0=0.
\bibitem{ann354}
Announcement 354(2017.2.8): What are $n = 2,1,0$ regular polygons inscribed in a disc? -- relations of $0$ and infinity.
\bibitem{362}
Announcement 362(2017.5.5): Discovery of the division by zero as
$0/0=1/0=z/0=0$.
\end{thebibliography}
\end{document}
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1
-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi
http://okmr.yamatoblog.net/
Relations of 0 and infinity
Hiroshi Okumura, Saburou Saitoh and Tsutomu Matsuura:
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…
https://sites.google.com/site/sandrapinelas/icddea-2017
2017.8.21.06:37

















































































0 件のコメント:
コメントを投稿