La crucial teoría matemática que enfrentó a dos titanes del siglo XVII: Isaac Newton y Gottfried Leibniz

Marcus du Sautoy, matemáticoSerie de la BBC "Breve historia de Matemáticas"

30 junio 2018

Concha de nautilinos — Image captionLa hermosa concha del nautilinos con su espiral logarítmica es la imagen clásica usada para ilustrar el desarrollo del cálculo.

Todo empezó en Europa a finales del siglo XVII. Dos excepcionales matemáticos estaban trabajando en el mismo problema al mismo tiempo.

Isaac Newton, ese gran héroe de la ciencia británica, tenía poco más de 20 años cuando comenzó a trabajar en una nueva rama de las matemáticas.

Newton se la describió a sus amigos, pero no publicó nada sobre ella.

Esa decisión más tarde tendría consecuencias desagradables pues, al mismo tiempo, el joven erudito alemán Gottfried Wilhelm Leibniz propuso una versión diferente de la misma cosa.

Se trataba del cálculo.

Si esa última palabra sólo te trae un vago recuerdo de algo que te enseñaron en el colegio o si te provoca terror, tratemos de remediarlo ya mismo de la mejor manera: a base de conocimiento.

¿Te gustan las matemáticas? No te pierdas:

Mujer asustada con un tablero lleno de fórmulas. — Image captionNo te asustes... no es un examen: ya vamos a recordar de qué se trata.

(Paréntesis para recordar qué es el cálculo)

En pocas palabras: el cálculo es una forma de describir las cosas que cambian.

Toma la famosa manzana que la leyenda dice que cayó del árbol sobre la cabeza del joven Newton e inspiró su teoría de la gravedad.

Caricatura de Newton cuando le cae la manzana en la cabeza — Image captionLa manzana más famosa después de la de Adán y Eva.

En cualquier momento en particular, ¿cuán rápido caía la manzana?

La velocidad de la manzana aumenta constantemente a medida que la gravedad la hala hacia el suelo. Entonces, ¿cómo puedes calcular cuál es la velocidad en un momento dado de tiempo, por ejemplo, después de un segundo?

La velocidad es la distancia recorrida dividida por el tiempo transcurrido.

Así que podrías registrar la distancia que la manzana cae en el próximo segundo y eso te daría una velocidad promedio durante ese período.

Pero si quieres la velocidad precisa en un momento preciso, podrías registrar la distancia recorrida en un período de tiempo más corto, digamos ½ segundo o ¼ de segundo. Cuanto menor es el intervalo de tiempo, más preciso es el cálculo de su velocidad.

En última instancia, para calcular la velocidad precisa en un momento preciso, necesitas tomar un intervalo de tiempo infinitamente pequeño.

El cálculo (infinitesimal) le da sentido a ese cálculo aparentemente imposible. Te dice a qué tiende la velocidad de algo, a medida que reduces el intervalo de tiempo.

El cálculo es la matemática de las cosas en movimiento.

Cruce de cables

En julio de 1676, Newton le envió una carta a Henry Oldenburg, el primer secretario de la Sociedad Real de Londres, en la que describía su versión del cálculo.

Para evitar compartir detalles sobre cómo funcionaba, lo convirtió en un código curioso.

"La base de estas operaciones es bastante evidente, de hecho; pero como no puedo continuar con la explicación ahora, he preferido ocultarlo así:

6accdae13eff7i3l9n4o4qrr4s8t12vx"

Isaac Newton — Image captionNewton había hecho público su conocimiento. En el siglo XVII, correspondencia e incluso divulgación frente a testigos confiables de manuscritos o instrumentos privados tenía un peso considerable; el trabajo no necesariamente tenía que ser publicado.

Oldenburg le envió la carta a Leibniz, aunque tardó 6 meses en hacerlo pues no sabía dónde encontrarlo: el matemático alemán estaba siempre viajando.

Al final la recibió y aunque lo que Newton había querido hacer era reclamar el cálculo como suyo sin revelar detalles, Leibniz no los necesitó. Él lo entendió.

Inmediatamente envió una respuesta entusiasta, expresando su admiración por lo que Newton había compartido y presentando algunos descubrimientos propios.

Pero habían pasado ya tantos meses que cuando Newton recibió la respuesta de Leibniz, no respondió.

Lo que podría haber sido el comienzo de un fructífero intercambio de ideas se frustró.

Gottfried Leibniz — Image captionCon el tiempo se ha establecido sin lugar a dudas que Newton desarrolló su "teoría de fluxiones" en 1665-6. Leibniz (en el retrato) llegó al cálculo de forma independiente durante el período de 1673-1676.

Leibniz comenzó a registrar su descubrimiento del cálculo, trabajando en él, intermitentemente, durante casi una década.

Cuando publicó sus estudios en 1684, la dinastía Bernouilli -una poderosa familia de matemáticos suizos- tomó sus ideas y las difundió ampliamente por todo el mundo matemático.

Leibniz comenzó a recibir crédito por esta nueva y poderosa rama de las matemáticas... algo que a Newton no le gustó.

No le gustó lo más mínimo

Newton en este momento estaba bien establecido como un gran científico.

Con solo 27 años, había sido galardonado con la prestigiosa cátedra Lucasian de matemáticas de la Universidad de Cambridge. Había publicado innumerables artículos científicos de gran importancia, incluidas sus leyes del movimiento y la famosa teoría universal de la gravitación.

Luego se convirtió en diputado y fue nombrado maestro de la Real Casa de la Moneda.

"No me gusta ser embaucado y burlado por extranjeros sobre cosas matemáticas", declaró.

Caricatura de Newton furioso — Image captionNewton se fue enfureciendo más y más con el tiempo. Durante años además, sus seguidores chocaban con los de Liebniz, por lo que se volvió una de las más grandes controversias de la historia de la ciencia.

En lugar de atribuirle a Leibniz su propia comprensión del cálculo, Newton decidió que Leibniz le había robado sus ideas y había pasado 6 meses trabajando en ellas antes de responderle.

En 1704, 20 años después de Leibniz, finalmente publicó su versión del cálculo, como un apéndice de su libro "Óptica: o un tratado de las reflexiones, refracciones, inflexiones y colores de la luz". En él, agregó un comentario que implicaba que Leibniz había copiado su trabajo:

"Hace algunos años presté un manuscrito que contenía tales teoremas sobre el cálculo y desde entonces me he encontrado con algunas cosas copiadas de él. En esta ocasión lo hice público".

Así comenzó una campaña de Newton para afirmar que, aunque Leibniz publicó antes que él, él era el inventor del cálculo.

Para Newton, compartir el crédito no era una opción.

Orgullo y prejuicio

En 1714, después de años de acrimonia y acusación, se le pidió a la Sociedad Real de Londres que resolviera entre las alegaciones rivales: ¿fue Newton el primero en descubrir el cálculo, con su método de fluxiones? ¿O se debía dar el crédito a Leibniz por su invención del método diferencial?

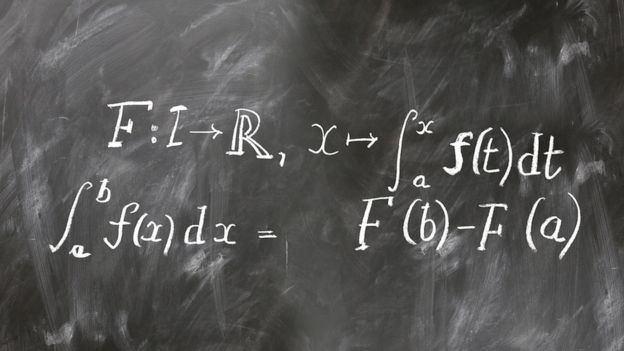Calculo, método diferencial — Image caption¿Es éste el método que debería llevarse los laureles?

"El método diferencial es el mismo que el de fluxiones, excepto en nombre y modo de anotación (...) por lo tanto asumimos que la pregunta adecuada (...)no es quién creó este método o el otro sino es quién fue el primer inventor del método (...)razón por la cual consideramos al Sr. Newton el primer inventor"

Leibniz, quien publicó su trabajo dos décadas antes que Newton, fue acusado de plagio y Newton fue honrado con el descubrimiento del cálculo.

No obstante, el informe de la Sociedad Real probablemente no era el más imparcial: el presidente de la organización en ese momento era Isaac Newton.

Cuando Newton murió en 1727, recibió un funeral de Estado y fue enterrado en la Abadía de Westminster con honores normalmente reservados para un general. El monumento de Leibniz, en contraste, es una placa simple en una pequeña iglesia en Hanover.

Pero fue la versión del erudito alemán del cálculo la que finalmente triunfó.

Leibniz tuvo la suerte de contar con el respaldo de la influyente familia Bernoulli, que se dio cuenta de cuán poderoso era el cálculo para encontrar la mejor solución a todo tipo de problemas.

Ese es el verdadero poder del cálculo: la capacidad de llegar a la solución más eficiente. Por eso se convirtió en una de las herramientas más importantes de toda la ciencia moderna.

El mundo natural está en constante estado de flujo, desde los planetas hasta el agua. Y si quieres comprenderlo y predecirlo, el cálculo es esencial.

Templo Liebniz en Hannover, Alemania — Image captionClaro que además de la humilde placa en una iglesia, se han erguido varios monumentos para recordar a Liebniz, como este templo en el Georgegarden en Hannover, Alemania.http://www.bbc.com/mundo/noticias-44560601

再生核研究所

2018年7月1日日曜日