Gauss, « le prince des mathématiciens »
Ce savant allemand du XVIIIe siècle est surtout connu pour ses travaux de théorie des nombres qui lui valent une admiration universelle et une influence vivace.
En savoir plus sur http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html#vKyfjRb1JOFq3yz7.99
En savoir plus sur http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html#vKyfjRb1JOFq3yz7.99
LE MONDE | | Par Michel Broué (Mathématicien, professeur émérite de l’université Paris-Diderot)
Abonnez vous à partir de 1 € Réagir Ajouter
Partager (57)Tweeter
image: http://img.lemde.fr/2018/03/14/0/0/446/676/534/0/60/0/c900da5_8020-9lg36i.dsk9.jpg

En savoir plus sur http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html#vKyfjRb1JOFq3yz7.99
Il est né en 1777, à l’apogée des Lumières. Dans une famille pauvre et d’une mère illettrée. Celui que tous s’accordent à appeler « le prince des mathématiciens » ne publia de son vivant qu’une partie de ses découvertes, immenses, fondatrices des mathématiques contemporaines. Il fut, par exemple, le premier à envisager des géométries non euclidiennes, en rupture avec la géométrie classique, mais ne publia pas ce travail « par crainte des cris des béotiens ».
Avant d’évoquer quelques-uns de ses travaux, je ne résiste pas à l’envie de raconter l’histoire de l’instituteur qui demanda à ses élèves, pensant les occuper un bout de temps, de calculer la somme des 100 premiers nombres : 1 + 2 + 3 +… + 100. Essayez, vous n’aurez pas la patience, et… quel intérêt ? L’élève Gauss n’avait pas 10 ans et, en bon mathématicien, n’eut ni patience ni intérêt… mais un peu d’insolence créatrice. « Pourquoi serais-je obligé de calculer cette somme dans l’ordre croissant des nombres ? Car si je calcule la somme du premier et du dernier (1 + 100), puis du deuxième et de l’avant-dernier (2 + 99), et ainsi de suite (3 + 98, etc.), chaque paire me donne la même somme, 101. Je dois faire cela 50 fois, le résultat est donc 50 × 101 = 5 050. » Ahurissement de l’instituteur, entendant le gamin donner le résultat en quelques minutes.
« Sublime science »
Essayons d’effleurer son œuvre. C’est dans le domaine des probabilités que son nom est le plus célèbre, avec la fameuse « courbe de Gauss », en cloche : il a décrit une loi modélisant des situations concrètes, dont la répartition est représentée par une telle courbe. On l’obtient, par exemple, en traçant l’histogramme des tailles d’une large population dont la taille moyenne est de 175 cm.
Mais ce sont ses travaux de théorie des nombres, ce cœur des mathématiques, qui lui valent une admiration universelle et une influence vivace. Impossible d’expliquer, ici, sa conjecture sur la répartition des nombres premiers, qui sera démontrée un siècle après sa formulation. Car, comme il l’écrivait : « Les charmes enchanteurs de cette sublime science ne se décèlent dans toute leur beauté qu’à ceux qui ont le courage de l’approfondir »…
Revenons à des résultats plus importants. Il a introduit la notion de « congruences ». Les « congruences modulo 12 » vous sont familières. Sur un cadran d’horloge, 12 et 0 sont confondus (12 = 0). Et on sait qu’à 15 heures l’horloge indique 3 ; au fond, parce que 15 = 12 + 3 = 0 + 3 = 3. Et puis, 11 = − 1… puisque 11 + 1 = 0, pardi. Si un événement commence lorsque l’horloge indique 4, et se prolonge consécutivement 3 fois pendant 11 heures, quelle heure indiquera l’horloge à la fin ? Réponse : 4 + (3 × 11) = 4 + (3 × − 1) = 4 − 3 = 1. L’horloge indiquera 1. Nous venons de faire des « calculs modulo 12 ». C’est le monde des congruences, outil de base de l’algèbre moderne… et du codage des transmissions numériques.
Astronome réputé et physicien de premier plan
C’est aussi en théoricien des nombres qu’il résolut, à 19 ans, une question venant de l’Antiquité grecque : quels sont les polygones réguliers (tels qu’un triangle équilatéral, un carré, un pentagone régulier, etc.) qui peuvent être construits avec une règle, un compas et un crayon ? Eh bien, il démontra entre autres que, pour un nombre de côtés égal à un « petit » nombre premier, ce n’est possible que pour les nombres 3, 5, 17 et 257. Le monde est ainsi fait, et Gauss et les mathématiques ont contribué à sa connaissance, parfois surprenante.
Ses talents de mathématicien firent de lui un astronome réputé. La plus petite planète naine du système solaire,Cérès, avait disparu. Introuvable. Gauss, à 25 ans, réussit à déterminer son orbite à l’aide de quelques données, et surtout des mathématiques. Il prédit où la trouver. Et en effet, on la retrouva à cet endroit.
Il fut aussi un physicien de premier plan, en particulier dans le domaine de l’électromagnétisme. Bref, s’il faut lister les « génies », il en est. Il fut un homme aussi, avec ses malheurs et ses grandeurs.
Profondément amoureux de sa première femme, il ne se remit guère de son décès prématuré et souffrit, semble-t-il, de dépression chronique. Mathématicien solitaire, il n’aima guère enseigner. Mais il forma des étudiants qui allaient aussi devenir des « princes », tel Bernhard Riemann, auteur de ce qui est sans doute la plus importante des conjectures mathématiques, « l’hypothèse de Riemann ».
La mathématicienne Sophie Germain, sa contemporaine, se cachait pour faire des mathématiques sous le nom masculin d’Antoine Auguste Le Blanc (impensable à l’époque qu’une femme fut mathématicienne !). Elle correspondit avec Gauss sous ce nom. Les troupes de Napoléon occupèrent Brunswick, où habitait Gauss. Craignant pour sa vie, Sophie Germain demanda à un général français de le protéger, et c’est ainsi que Gauss apprit qu’Antoine était Sophie. Il lui écrivit alors : « Lorsqu’une personne de ce sexe qui, par nos mœurs et nos préjugés, doit rencontrer infiniment plus d’obstacles et de difficultés que les hommes à se familiariser avec ces recherches épineuses, sait néanmoins franchir ces entraves et pénétrer ce qu’elles ont de plus caché, il faut sans doute qu’elle ait le plus noble courage, des talents tout à fait extraordinaires, le génie supérieur. » Génie, et homme de bien.
En savoir plus sur http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html#vKyfjRb1JOFq3yz7.99
http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html
Avant d’évoquer quelques-uns de ses travaux, je ne résiste pas à l’envie de raconter l’histoire de l’instituteur qui demanda à ses élèves, pensant les occuper un bout de temps, de calculer la somme des 100 premiers nombres : 1 + 2 + 3 +… + 100. Essayez, vous n’aurez pas la patience, et… quel intérêt ? L’élève Gauss n’avait pas 10 ans et, en bon mathématicien, n’eut ni patience ni intérêt… mais un peu d’insolence créatrice. « Pourquoi serais-je obligé de calculer cette somme dans l’ordre croissant des nombres ? Car si je calcule la somme du premier et du dernier (1 + 100), puis du deuxième et de l’avant-dernier (2 + 99), et ainsi de suite (3 + 98, etc.), chaque paire me donne la même somme, 101. Je dois faire cela 50 fois, le résultat est donc 50 × 101 = 5 050. » Ahurissement de l’instituteur, entendant le gamin donner le résultat en quelques minutes.
« Sublime science »
Essayons d’effleurer son œuvre. C’est dans le domaine des probabilités que son nom est le plus célèbre, avec la fameuse « courbe de Gauss », en cloche : il a décrit une loi modélisant des situations concrètes, dont la répartition est représentée par une telle courbe. On l’obtient, par exemple, en traçant l’histogramme des tailles d’une large population dont la taille moyenne est de 175 cm.
Mais ce sont ses travaux de théorie des nombres, ce cœur des mathématiques, qui lui valent une admiration universelle et une influence vivace. Impossible d’expliquer, ici, sa conjecture sur la répartition des nombres premiers, qui sera démontrée un siècle après sa formulation. Car, comme il l’écrivait : « Les charmes enchanteurs de cette sublime science ne se décèlent dans toute leur beauté qu’à ceux qui ont le courage de l’approfondir »…
Revenons à des résultats plus importants. Il a introduit la notion de « congruences ». Les « congruences modulo 12 » vous sont familières. Sur un cadran d’horloge, 12 et 0 sont confondus (12 = 0). Et on sait qu’à 15 heures l’horloge indique 3 ; au fond, parce que 15 = 12 + 3 = 0 + 3 = 3. Et puis, 11 = − 1… puisque 11 + 1 = 0, pardi. Si un événement commence lorsque l’horloge indique 4, et se prolonge consécutivement 3 fois pendant 11 heures, quelle heure indiquera l’horloge à la fin ? Réponse : 4 + (3 × 11) = 4 + (3 × − 1) = 4 − 3 = 1. L’horloge indiquera 1. Nous venons de faire des « calculs modulo 12 ». C’est le monde des congruences, outil de base de l’algèbre moderne… et du codage des transmissions numériques.
Astronome réputé et physicien de premier plan
C’est aussi en théoricien des nombres qu’il résolut, à 19 ans, une question venant de l’Antiquité grecque : quels sont les polygones réguliers (tels qu’un triangle équilatéral, un carré, un pentagone régulier, etc.) qui peuvent être construits avec une règle, un compas et un crayon ? Eh bien, il démontra entre autres que, pour un nombre de côtés égal à un « petit » nombre premier, ce n’est possible que pour les nombres 3, 5, 17 et 257. Le monde est ainsi fait, et Gauss et les mathématiques ont contribué à sa connaissance, parfois surprenante.
Ses talents de mathématicien firent de lui un astronome réputé. La plus petite planète naine du système solaire,Cérès, avait disparu. Introuvable. Gauss, à 25 ans, réussit à déterminer son orbite à l’aide de quelques données, et surtout des mathématiques. Il prédit où la trouver. Et en effet, on la retrouva à cet endroit.
Il fut aussi un physicien de premier plan, en particulier dans le domaine de l’électromagnétisme. Bref, s’il faut lister les « génies », il en est. Il fut un homme aussi, avec ses malheurs et ses grandeurs.
Profondément amoureux de sa première femme, il ne se remit guère de son décès prématuré et souffrit, semble-t-il, de dépression chronique. Mathématicien solitaire, il n’aima guère enseigner. Mais il forma des étudiants qui allaient aussi devenir des « princes », tel Bernhard Riemann, auteur de ce qui est sans doute la plus importante des conjectures mathématiques, « l’hypothèse de Riemann ».
La mathématicienne Sophie Germain, sa contemporaine, se cachait pour faire des mathématiques sous le nom masculin d’Antoine Auguste Le Blanc (impensable à l’époque qu’une femme fut mathématicienne !). Elle correspondit avec Gauss sous ce nom. Les troupes de Napoléon occupèrent Brunswick, où habitait Gauss. Craignant pour sa vie, Sophie Germain demanda à un général français de le protéger, et c’est ainsi que Gauss apprit qu’Antoine était Sophie. Il lui écrivit alors : « Lorsqu’une personne de ce sexe qui, par nos mœurs et nos préjugés, doit rencontrer infiniment plus d’obstacles et de difficultés que les hommes à se familiariser avec ces recherches épineuses, sait néanmoins franchir ces entraves et pénétrer ce qu’elles ont de plus caché, il faut sans doute qu’elle ait le plus noble courage, des talents tout à fait extraordinaires, le génie supérieur. » Génie, et homme de bien.
En savoir plus sur http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html#vKyfjRb1JOFq3yz7.99
http://www.lemonde.fr/mathematiques/article/2018/03/21/gauss-le-prince-des-mathematiciens_5274092_1650729.html
とても興味深く読みました:
ゼロ除算の発見と重要性を指摘した:日本、再生核研究所
ダ・ヴィンチの名言 格言|無こそ最も素晴らしい存在
ゼロ除算の発見はどうでしょうか:
Black holes are where God divided by zero:
再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議
https://ameblo.jp/syoshinoris/entry-12287338180.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html
ソクラテス・プラトン・アリストテレス その他
https://ameblo.jp/syoshinoris/entry-12328488611.html
ドキュメンタリー 2017: 神の数式 第2回 宇宙はなぜ生まれたのか
https://www.youtube.com/watch?v=iQld9cnDli4
〔NHKスペシャル〕神の数式 完全版 第3回 宇宙はなぜ始まったのか
https://www.youtube.com/watch?v=DvyAB8yTSjs&t=3318s
〔NHKスペシャル〕神の数式 完全版 第1回 この世は何からできているのか
https://www.youtube.com/watch?v=KjvFdzhn7Dc
NHKスペシャル 神の数式 完全版 第4回 異次元宇宙は存在するか
https://www.youtube.com/watch?v=fWVv9puoTSs
再生核研究所声明 411(2018.02.02): ゼロ除算発見4周年を迎えて
https://ameblo.jp/syoshinoris/entry-12348847166.html
再生核研究所声明 416(2018.2.20): ゼロ除算をやってどういう意味が有りますか。何か意味が有りますか。何になるのですか - 回答
再生核研究所声明 417(2018.2.23): ゼロ除算って何ですか - 中学生、高校生向き 回答
再生核研究所声明 418(2018.2.24): 割り算とは何ですか? ゼロ除算って何ですか - 小学生、中学生向き 回答
再生核研究所声明 420(2018.3.2): ゼロ除算は正しいですか,合っていますか、信用できますか - 回答
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
私は数学を信じない。 アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。
1423793753.460.341866474681。
Einstein's Only Mistake: Division by Zero
2018.3.18.午前中 最後の講演: 日本数学会 東大駒場、函数方程式論分科会 講演書画カメラ用 原稿
The Japanese Mathematical Society, Annual Meeting at the University of Tokyo. 2018.3.18.
https://ameblo.jp/syoshinoris/entry-12361744016.html より
再生核研究所声明 424(2018.3.29): レオナルド・ダ・ヴィンチとゼロ除算
2018.3.18.午前中 最後の講演: 日本数学会 東大駒場、函数方程式論分科会 講演書画カメラ用 原稿
The Japanese Mathematical Society, Annual Meeting at the University of Tokyo. 2018.3.18.
https://ameblo.jp/syoshinoris/entry-12361744016.html より
The Japanese Mathematical Society, Annual Meeting at the University of Tokyo. 2018.3.18.
https://ameblo.jp/syoshinoris/entry-12361744016.html より
*057 Pinelas,S./Caraballo,T./Kloeden,P./Graef,J.(eds.): Differential and Difference Equations with Applications: ICDDEA, Amadora, 2017. (Springer Proceedings in Mathematics and Statistics, Vol. 230) May 2018 587 pp.
#divide by zero
TOP DEFINITION
A super-smart math teacher that teaches at HTHS and can divide by zero.
Hey look, that genius’s IQ is over 9000!
by Lawlbags! October 21, 2009
Dividing by zero is the biggest epic fail known to mankind. It is a proven fact that a succesful division by zero will constitute in the implosion of the universe.
You are dividing by zero there, Johnny. Captain Kirk is not impressed.
Divide by zero?!?!! OMG!!! Epic failzorz
Divide by zero?!?!! OMG!!! Epic failzorz
3
Divide by zero is undefined.
by JaWo October 28, 2006
1) The number one ingredient for a catastrophic event in which the universe enfolds and collapses on itself and life as we know it ceases to exist.
2) A mathematical equation such as a/0 whereas a is some number and 0 is the divisor. Look it up on Wikipedia or something. Pretty confusing shit.
3) A reason for an error in programming
2) A mathematical equation such as a/0 whereas a is some number and 0 is the divisor. Look it up on Wikipedia or something. Pretty confusing shit.
3) A reason for an error in programming
Hey, I divided by zero! ...Oh shi-
a/0
Run-time error: '11': Division by zero
a/0
Run-time error: '11': Division by zero
by DefectiveProduct September 08, 2006
When even math shows you that not everything can be figured out with math. When you divide by zero, math kicks you in the shins and says "yeah, there's kind of an answer, but it ain't just some number."
It's when mathematicians become philosophers.
It's when mathematicians become philosophers.
Math:
Let's say you have ZERO apples, and THREE people. How many apples does each person get? ZERO, cause there were no apples to begin with
Not-math because of dividing by zero:
Let's say there are THREE apples, and ZERO people. How many apples does each person get? Friggin... How the Fruitcock should I know! How can you figure out how many apples each person gets if there's no people to get them?!? You'd think it'd be infinity, but not really. It could almost be any number, cause you could be like "each person gets 400 apples" which would be true, because all the people did get 400 apples, because there were no people. So all the people also got 42 apples, and a million and 7 apples. But it's still wrong.
Let's say you have ZERO apples, and THREE people. How many apples does each person get? ZERO, cause there were no apples to begin with
Not-math because of dividing by zero:
Let's say there are THREE apples, and ZERO people. How many apples does each person get? Friggin... How the Fruitcock should I know! How can you figure out how many apples each person gets if there's no people to get them?!? You'd think it'd be infinity, but not really. It could almost be any number, cause you could be like "each person gets 400 apples" which would be true, because all the people did get 400 apples, because there were no people. So all the people also got 42 apples, and a million and 7 apples. But it's still wrong.
#math #divide by zero #divide #dividing #zero #numbers #not-math #imaginary numbers #imaginary. phylosophy
by Zacharrie February 15, 2010




















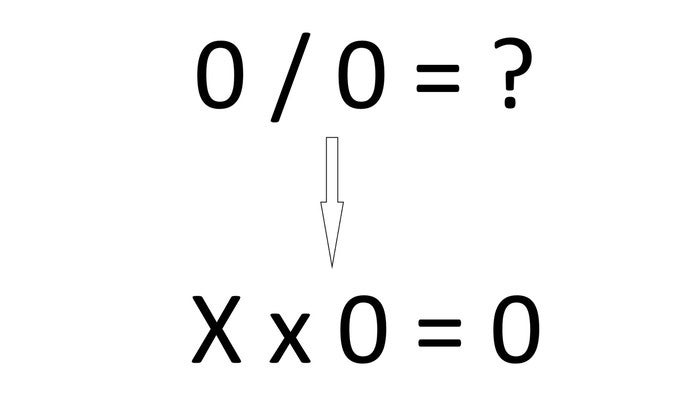









0 件のコメント:
コメントを投稿