第一个数学力学问题:倍立方体
公元前3世纪希腊天文学家、数学家、地理学之父埃拉托色尼(Eratosthenes ofCyrene. c. 276 BC – c. 195/194 BC)在Platonicus中记录了希腊提洛斯岛(Delos,传说是太阳神阿波罗的出生地)发生了一次瘟疫,当居民向阿波罗祈祷时,神谕说:“他们需要把正方体的祭坛加到两倍,瘟疫才能停止”。
图1 埃拉托色尼 wiki百科
现在我们知道,正方体体积翻倍其边长需要变为原长的(2开3次方)倍,但是,当时人们还不会开立方,该问题被限定在尺规作图法内完成。这可难坏了当时的工匠们,有人尝试把祭坛的边长变成原来的2倍,此时体积将是原来的8倍;如果再做一个等大的正方体虽可以体积翻倍,却不能得到正方体。这个问题太难了,当提洛斯岛的居民去请教当时的最著名的柏拉图,柏拉图也一筹莫展,只好说:神并不是让大家真正做一个两倍的祭坛,只是因为希腊人过于忽视数学和几何的作用,以此神要大家重视数学和几何。
对于倍立方体迈出第一步的是古希腊数学家希波克拉底(Hippocrates of Chios,c. 470 – c. 410 BCE.),注意他不是提出希波克拉底宣言(医生都要宣誓遵守的职业道德)的医学家希波克拉底(Hippocrates of Kos,c. 460 – c. 370 BC),数学家希波克拉底比医学家希波克拉底大了约10岁。数学家希波克拉底将倍立方体问题做了一点变动,将问题转化为寻找两条线段长度的两个比例中项(当a:x=x:b,则x就是a和b的比例中项),他这样提问:
图2 希波克拉底
假设a,b代表两条线段的长度,当x,y是a,b的两个比例中项时,即a:x=x:y=y:b;观察这个连比:其一,三个比相乘(a: x)(x : y)(y: b)=a :b;其二,(x:y)和(y:b)均等于(a:x),三个比相乘又可以等于(a:x)3=a3: x3。这两步说明,a3: x3= a :b。可见,当a :b=1:2时,x=(2开3次方)a,也就是说当a为原立方体边长时,x就是新立方体的边长。
此后希波克拉底就努力用尺规作图法去寻找a,b之间的两个比例中项。当时人们已知求解两数的一个比例中项的方法,例如以AC为直径的半圆 ABC,则可知∠ABC为直角,过B点作AC的垂线BH,则△ABH相似于△BCH三角形,因此有AH:BH=BH:HC,因此BH就是AH和HC的比例中项,这在后来被称为射影定理。
图3
找一个比例中项相对容易,但要找到两个比例中项解决倍立方体就不那么容易了。希波克拉底最后也没有解决该问题。虽然希波克拉底没能找到他设定的两个比例中项,但后来致力于解决倍立方体的数学家都沿用了希波克拉底寻找两个比例中项的思路。他还部分解决了化圆为方问题(古希腊三大数学难题:化圆为方、倍立方体、三等分角),并第一次系统的撰写了几何学(Element),他之后至少有4位数学家撰写几何学(Element),欧几里得的《几何原本》(Element)是建立在这些前人研究基础之上的。
最终解决倍立方体问题的是被誉为数学力学家的阿契塔(请参见力学源头说力学属性、阿契塔的机械鸽、阿契塔的音乐实践),而且他在空间作图,是所有解(与后来解决该问题的解相比)中最为独特的一种。为了便于说明,我们借用一些现代我们熟悉的工具,例如坐标系,因为当时还没有坐标系。考虑图4所示坐标系A-xyz,在xAy平面内作一个直径为AD的圆,做弦AB,这里AB=a,AD=b。目标是寻找a,b之间的两个比例中项。过D点做圆ABD的切线与AB的延长线交于P。然后,转到A-xyz空间中,考虑以下几个步骤:
图4 底面
图5 阿契塔的立体作图 注y轴没有画出,坐标系满足右手坐标系统
图6 直角三角形中找两个比例中项
这个问题的解决,不只是倍立方体,实际上任意倍的立方体都可以求,只需要设定a:b的值,也就是图5中AB与AD的比值。它的意义又不局限于规则几何体,对于非规则的几何体也可以求任意倍体积,只需要求特征边长需要扩大或者缩小的倍数即可。这一方法在工业制造中非常有用,在阿契塔的时代,在机械制造和建筑设计中,人们很可能是制作出模型然后再建造大的实物以弥补设计手段的不足,如果理解了几何体边长与体积之间的尺寸关系,就可以方便的从模型尺寸推导出任意体积大小的实物尺寸。这样,倍立方体在建筑设计或机械设计中的重要意义是显而易见的。后世力学家帕普斯(Pappus of Alexandria.c. 290 – c. 350 AD)将倍立方体的解视为实用力学最为重要几何理论之一,这很可能是第一个直接为实用力学服务的数学原理(Huffman, Carl,"Archytas")。阿契塔也以此被享有西方司马迁美誉的罗马传记文学家普鲁塔克(Plutarch,46-120A.D.)称为数学力学的奠基人。
倍立方体本身魅力无穷,它不仅奠定了数学力学,同时还开创了立体几何,后世对倍立方体的进一步研究还导致了圆锥曲线理论的诞生。古希腊数学家Eutocius of Ascalon(c. 480-c. 540)搜集了倍立方体问题的11种求解方法。毫无疑问,阿契塔的求解方法在空间构造比例中项,开创了立体几何;他的学生欧多克索斯(Eudoxus of Cnidus, 408BC - 355 BC)将阿契塔的空间结构投影到平面得到了平面上的解;欧多克斯的学生门奈赫莫斯(Menaechmus, 380–320 BC)继续研究倍立方体,又开创了圆锥曲线的研究。门奈赫莫斯注意到希波克拉底的连比a:x=x:y=y:b,前一个等号可导出
x2=ay (1)
后一个等号可导出
y2=bx (2)
这两个方程表示抛物线。第1个比等于第3个比导出
xy=ab (3)
这是双曲线。选择(1)~(3)式中任意两个,连列方程,求出x就解决了倍立方体问题。我们也借用一下我们现在已有的方法去理解门奈赫莫斯的方法。将(1),(2)和(3)所表示的曲线绘制在同一个坐标系中,如图7所示(当然门奈赫莫斯也没有用到坐标系),
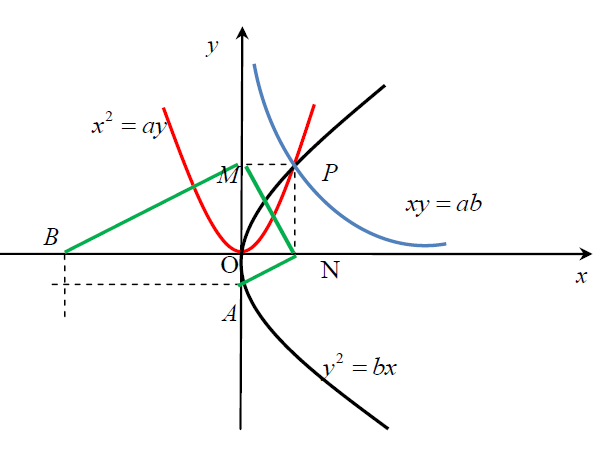
图7
方程(1)-(3)两两求解,可得三条曲线相交于同一点P,则P点的横坐标x(图中ON的长)就是我们要求的解。过P点作PN⊥Ox于N,作PM⊥Oy于M。连接MN,过M作MB⊥MN交x轴于B点,过N作NA⊥MN交y轴于A点。现在擦除圆锥曲线,只留下辅助线,如图8.
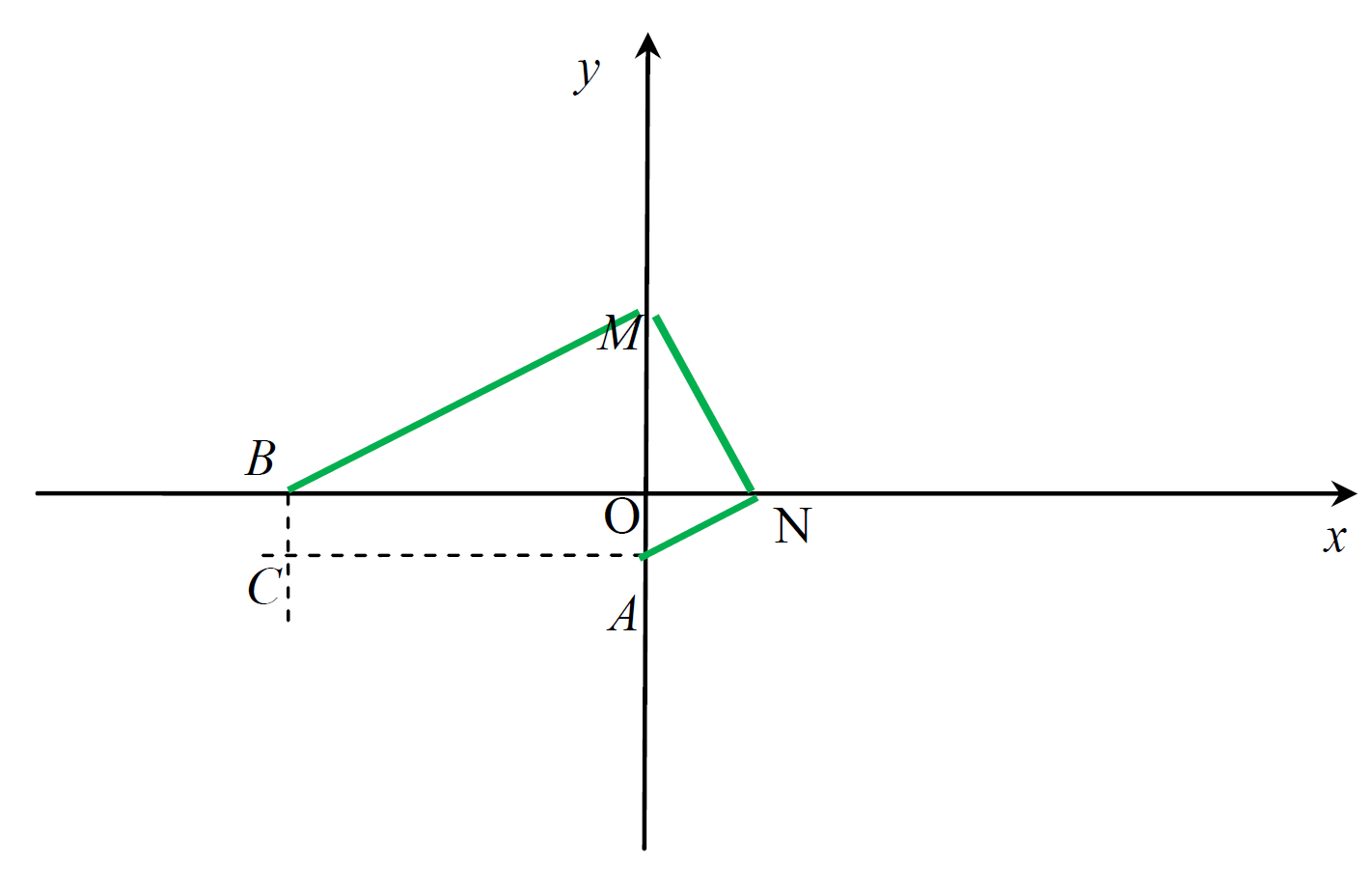
图8
依据相似三角形有:OA:ON=ON:OM;又有OA:ON=OM:OB。因此可以得到:OA:ON=ON:OM=OM:OB,假设OA=a, OB=b时,ON就是想要的解。门奈赫莫斯的解法给了希腊人利用机械求解倍立方体的思路,只需要制作两把直角尺和一个十字架(画出两条相交的线也可以),如图9所示。设定OA=a,OB=b,两直尺如图9放置,保证两个直角尺的一边分别通过B、A两点,移动直角尺使得另两边重合且两直角落在两十字相交的线上,此时ON就是所求的解。
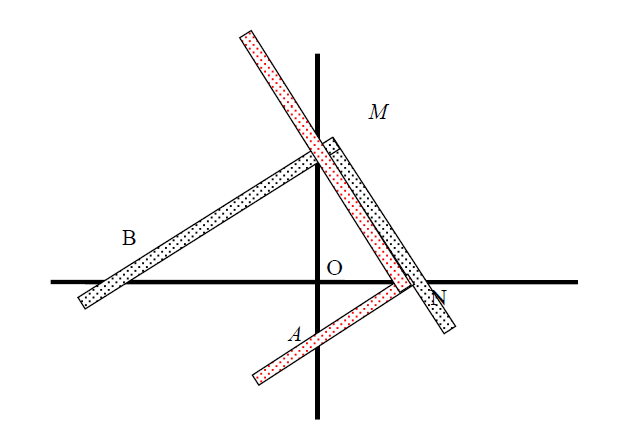
图9
显然,虽然倍立方体问题的提法是希望将体积翻2倍,但该问题的解决实际上可以求解任意倍的体积问题,只需要将a:b的倍数做相应的设定即可。令人惊叹的是,从希波克拉底到阿契塔,再到欧多克索斯、门奈赫莫斯,几代人的努力在解决同一个“古老”的问题,并且由此诞生出来立体几何、圆锥曲线,以及求解几何问题的机械方法等分支,这对于我们至少有两点启示:一是我们总习惯于寻找标准答案,假如一个问题的解答被标准化了,可能就不会诞生新的学科了;其次,我们也会听到人们对于某些科研评价时说:“这些问题早已被人研究过了,没什么研究价值了”,联想着倍立方体,我们可能真的要问:“这些问题真的没有研究价值了吗?”
参考资料
http://www-history.mcs.st-and.ac.uk/HistTopics/Doubling_the_cube.html
https://en.wikipedia.org/wiki/Hippocrates_of_Chios
Huffman,Carl, "Archytas", The Stanford Encyclopedia of Philosophy, Edward N.Zalta (ed.)
https://en.wikipedia.org/wiki/Archytas
杜瑞芝, 王青建, 孙宏安. 简明数学史辞典[M]. 山东教育出版社, 1991.
[美]卡尔.B.博耶(著).秦传安(译).数学史.中央编译出版社. 2012
百度文库. 倍立方体的历史解法
とても興味深く読みました:
再生核研究所声明306(2016.06.21) 平行線公理、非ユークリッド幾何学、そしてゼロ除算
表題について、山間部を散歩している折り新鮮な感覚で、想いが湧いて来た。新しい幾何学の発見で、ボーヤイ・ヤーノシュが父に言われた 平行線の公理を証明できたら、地球の大きさ程のダイヤモンドほどの値打ちがあると言われて、敢然と証明に取り掛かった姿とその帰結である。また、ユークリッドが海岸を散歩しながら幾何学を建設していく情景が鮮やかに想い出された(Liwanovaの『新しい幾何学の発見』(のちに『ロバチェフスキーの世界』と改題)(東京図書刊行)。この件、既に声明に述べているので、まずは確認したい:
再生核研究所声明292(2016.03.25) ユークリッド幾何学、非ユークリッド幾何学、平行線公理、そしてゼロ除算(2016.3.23 朝、目を覚まして、情念と構想が閃いたものである。)
まず基本語をウイキペデアで確認して置こう:
https://ja.wikipedia.org/wiki/%E3%82%A8%E3%82%A6%E3%82%AF%E3%83%AC%E3%82%A4%E3%83%87%E3%82%B9
アレクサンドリアのエウクレイデス(古代ギリシャ語: Εὐκλείδης, Eukleídēs、ラテン語: Euclīdēs、英語: Euclid(ユークリッド)、紀元前3世紀? - )は、古代ギリシアの数学者、天文学者とされる。数学史上最も重要な著作の1つ『原論』(ユークリッド原論)の著者であり、「幾何学の父」と称される。プトレマイオス1世治世下(紀元前323年-283年)のアレクサンドリアで活動した。『原論』は19世紀末から20世紀初頭まで数学(特に幾何学)の教科書として使われ続けた。
https://ja.wikipedia.org/wiki/%E9%9D%9E%E3%83%A6%E3%83%BC%E3%82%AF%E3%83%AA%E3%83%83%E3%83%89%E5%
非ユークリッド幾何学の成立: ニコライ・イワノビッチ・ロバチェフスキーは「幾何学の新原理並びに平行線の完全な理論」(1829年)において、「虚幾何学」と名付けられた幾何学を構成して見せた。これは、鋭角仮定を含む幾何学であった。ボーヤイ・ヤーノシュは父・ボーヤイ・ファルカシュの研究を引き継いで、1832年、「空間論」を出版した。「空間論」では、平行線公準を仮定した幾何学(Σ)、および平行線公準の否定を仮定した幾何学(S)を論じた。更に、1835年「ユークリッド第 11 公準を証明または反駁することの不可能性の証明」において、Σ と S のどちらが現実に成立するかは、如何なる論理的推論によっても決定されないと証明した。
ユークリッド幾何学は 2000年を超えて数学及び論理と あらゆる科学の記述の基礎になってきた。その幾何学を支える平行線の公理については、非ユークリッド幾何学の成立過程で徹底的に検討、議論され、逆に 平行線の公理がユークリッド幾何学の特徴的な仮定(仮説)で証明できない公理であることが明らかにされた。それとともに 数学とは何かに対する認識が根本的に変わり、数学とは公理系(仮説系)の上に建設された理論体系であって、絶対的な真理という概念を失った。
ここで焦点を当てたいのは 平行線の概念である。ユークリッド幾何学における平行線とは 任意の直線に対して、直線上以外の点を通って、それと交わらない直線のことで、平行線がただ1つ存在するというのがユークリッドの公理である。非ユークリッド幾何学では、そのような平行線が全然存在しなかったり、沢山存在する幾何学になっており、そのような幾何学は 実在し、現在も盛んに利用されている。
この平行線の問題が、ゼロ除算の発見1/0=0、台頭によって 驚嘆すべき、形相を帯びてきた。
ユークリッド自身、また、非ユークリッド幾何学の上記発見者たち、それに自ら深い研究をしていた天才ガウスにとっても驚嘆すべき事件であると考えられる。
何と ユークリッド空間で 平行線は ある意味で全て原点で交わっている という、現象が明らかにされた。
もちろん、ここで交わっていることの意味を 従来の意味にとれば、馬鹿馬鹿しいことになる。
そこで、その意味をまず、正確に述べよう。まずは、 イメージから述べる。リーマン球面に立体射影させると 全ユークリッド平面は 球面から北極点を除いた球面上に一対一に写される。そのとき、球面の北極点に対応する点が平面上になく、想像上の点として無限遠点を付け加えて対応させれば、立体射影における円、円対応を考えれば、平面上の平行線は無限遠点で交わっているとして、すっきりと説明され、複素解析学における基本的な世界観を与えている。平行線は無限遠点で 角ゼロ(度)で交わっている(接している)も立体射影における等角性で保証される。あまりの美しさのため、100年を超えて疑われることはなく、世の全ての文献はそのような扱いになっていて数学界の定説である。
ところがゼロ除算1/0=0では 無限遠点は空間の想像上の点として、存在していても、その点、無限遠点は数値では ゼロ(原点)に対応していることが明らかにされた。 すなわち、北極(無限遠点)は南極(原点)と一致している。そのために、平行線は原点で交わっていると解釈できる。もちろん、全ての直線は原点を通っている。
この現象はユークリッド空間の考えを改めるもので、このような性質は解析幾何学、微積分学、複素解析学、物理学など広範に影響を与え、統一的に新しい秩序ある世界を構成していることが明らかにされた。2200年を超えて、ユークリッド幾何学に全く新しい局面が現れたと言える。
平行線の交わりを考えてみる。交わる異なる2直線を1次方程式で書いて、交点の座標を求めて置く。その座標は、平行のとき、分母がゼロになって、交点の座標が求まらないと従来ではなっていたが、ゼロ除算では、それは可能で、原点(0,0)が対応すると解釈できる。ゼロ除算と解析幾何学からの帰結である。上記幾何学的な説明が、ゼロ除算で解析幾何学的にも導かれる。
一般の円の方程式を2次関数で表現すれば、(x^2+y^2) の係数がゼロの場合、直線の一般式になるが、ゼロ除算を用いると、それが保証されるばかりか、直線の中心は 原点である、直線も点円も曲率がゼロであることが導かれる。もちろん、ゼロ除算の世界では、全ての直線は原点を通っている。このとき、原点を無限遠点の映った影ともみなせ、原点はこのような意味で もともとの原点とこの意味での点としての、2重性を有し、この概念は今後大きな意味を有することになるだろう。
ゼロ除算1/0=0は ユークリッド幾何学においても、大きな変革を求めている。
以上
上記で、数学的に大事な観点は、ユークリッド自身そうであったが、平行線公理は真理で、証明されるべきもの、幾何学は絶対的な真理であると非ユークリッド幾何学の出現まで、考えられてきたということである。2000年を超える世界観であった事実である。そこで、平行線の公理を証明しようと多くの人が挑戦してきたが、非ユークリッド幾何学の出現まで不可能であった。実は、証明できない命題であったという全く意外な帰結であった。真に新しい、概念、世界観であった。証明できない命題の存在である。それこそ、世界観を変える、驚嘆すべき世界史上の事件であったと言える。
この事件に関してゼロ除算の発見は、全く異なる世界観を明らかにしている。ユークリッドそして、非ユークリッド幾何学の3人の発見者にとって、全く想像ができなかった、新しい事実である。平行線が 無限の先で交わっているとは ユークリッドは考えなかったと思われるが、近代では、無限の先で交わっていると考えられて来ている。― これには、アーベル、オイラー、リーマンなどの考えが存在する。このような考えは、ここ100年以上、世界の常識、定説になっている。ところがゼロ除算では、無限遠点は 数ではゼロが対応していて、平行線は代数的に原点で交わっている、すべての直線は代数的に原点を通っているという解釈が成り立つことを示している。
ユークリッドの幾何学の建設時の想い、ボーヤイ・ヤーノシュの激しい挑戦の様を、 想い を 深く、いろいろ想像している。
以 上
Matrices and Division by Zero z/0 = 0
表題について、山間部を散歩している折り新鮮な感覚で、想いが湧いて来た。新しい幾何学の発見で、ボーヤイ・ヤーノシュが父に言われた 平行線の公理を証明できたら、地球の大きさ程のダイヤモンドほどの値打ちがあると言われて、敢然と証明に取り掛かった姿とその帰結である。また、ユークリッドが海岸を散歩しながら幾何学を建設していく情景が鮮やかに想い出された(Liwanovaの『新しい幾何学の発見』(のちに『ロバチェフスキーの世界』と改題)(東京図書刊行)。この件、既に声明に述べているので、まずは確認したい:
再生核研究所声明292(2016.03.25) ユークリッド幾何学、非ユークリッド幾何学、平行線公理、そしてゼロ除算(2016.3.23 朝、目を覚まして、情念と構想が閃いたものである。)
まず基本語をウイキペデアで確認して置こう:
https://ja.wikipedia.org/wiki/%E3%82%A8%E3%82%A6%E3%82%AF%E3%83%AC%E3%82%A4%E3%83%87%E3%82%B9
アレクサンドリアのエウクレイデス(古代ギリシャ語: Εὐκλείδης, Eukleídēs、ラテン語: Euclīdēs、英語: Euclid(ユークリッド)、紀元前3世紀? - )は、古代ギリシアの数学者、天文学者とされる。数学史上最も重要な著作の1つ『原論』(ユークリッド原論)の著者であり、「幾何学の父」と称される。プトレマイオス1世治世下(紀元前323年-283年)のアレクサンドリアで活動した。『原論』は19世紀末から20世紀初頭まで数学(特に幾何学)の教科書として使われ続けた。
https://ja.wikipedia.org/wiki/%E9%9D%9E%E3%83%A6%E3%83%BC%E3%82%AF%E3%83%AA%E3%83%83%E3%83%89%E5%
非ユークリッド幾何学の成立: ニコライ・イワノビッチ・ロバチェフスキーは「幾何学の新原理並びに平行線の完全な理論」(1829年)において、「虚幾何学」と名付けられた幾何学を構成して見せた。これは、鋭角仮定を含む幾何学であった。ボーヤイ・ヤーノシュは父・ボーヤイ・ファルカシュの研究を引き継いで、1832年、「空間論」を出版した。「空間論」では、平行線公準を仮定した幾何学(Σ)、および平行線公準の否定を仮定した幾何学(S)を論じた。更に、1835年「ユークリッド第 11 公準を証明または反駁することの不可能性の証明」において、Σ と S のどちらが現実に成立するかは、如何なる論理的推論によっても決定されないと証明した。
ユークリッド幾何学は 2000年を超えて数学及び論理と あらゆる科学の記述の基礎になってきた。その幾何学を支える平行線の公理については、非ユークリッド幾何学の成立過程で徹底的に検討、議論され、逆に 平行線の公理がユークリッド幾何学の特徴的な仮定(仮説)で証明できない公理であることが明らかにされた。それとともに 数学とは何かに対する認識が根本的に変わり、数学とは公理系(仮説系)の上に建設された理論体系であって、絶対的な真理という概念を失った。
ここで焦点を当てたいのは 平行線の概念である。ユークリッド幾何学における平行線とは 任意の直線に対して、直線上以外の点を通って、それと交わらない直線のことで、平行線がただ1つ存在するというのがユークリッドの公理である。非ユークリッド幾何学では、そのような平行線が全然存在しなかったり、沢山存在する幾何学になっており、そのような幾何学は 実在し、現在も盛んに利用されている。
この平行線の問題が、ゼロ除算の発見1/0=0、台頭によって 驚嘆すべき、形相を帯びてきた。
ユークリッド自身、また、非ユークリッド幾何学の上記発見者たち、それに自ら深い研究をしていた天才ガウスにとっても驚嘆すべき事件であると考えられる。
何と ユークリッド空間で 平行線は ある意味で全て原点で交わっている という、現象が明らかにされた。
もちろん、ここで交わっていることの意味を 従来の意味にとれば、馬鹿馬鹿しいことになる。
そこで、その意味をまず、正確に述べよう。まずは、 イメージから述べる。リーマン球面に立体射影させると 全ユークリッド平面は 球面から北極点を除いた球面上に一対一に写される。そのとき、球面の北極点に対応する点が平面上になく、想像上の点として無限遠点を付け加えて対応させれば、立体射影における円、円対応を考えれば、平面上の平行線は無限遠点で交わっているとして、すっきりと説明され、複素解析学における基本的な世界観を与えている。平行線は無限遠点で 角ゼロ(度)で交わっている(接している)も立体射影における等角性で保証される。あまりの美しさのため、100年を超えて疑われることはなく、世の全ての文献はそのような扱いになっていて数学界の定説である。
ところがゼロ除算1/0=0では 無限遠点は空間の想像上の点として、存在していても、その点、無限遠点は数値では ゼロ(原点)に対応していることが明らかにされた。 すなわち、北極(無限遠点)は南極(原点)と一致している。そのために、平行線は原点で交わっていると解釈できる。もちろん、全ての直線は原点を通っている。
この現象はユークリッド空間の考えを改めるもので、このような性質は解析幾何学、微積分学、複素解析学、物理学など広範に影響を与え、統一的に新しい秩序ある世界を構成していることが明らかにされた。2200年を超えて、ユークリッド幾何学に全く新しい局面が現れたと言える。
平行線の交わりを考えてみる。交わる異なる2直線を1次方程式で書いて、交点の座標を求めて置く。その座標は、平行のとき、分母がゼロになって、交点の座標が求まらないと従来ではなっていたが、ゼロ除算では、それは可能で、原点(0,0)が対応すると解釈できる。ゼロ除算と解析幾何学からの帰結である。上記幾何学的な説明が、ゼロ除算で解析幾何学的にも導かれる。
一般の円の方程式を2次関数で表現すれば、(x^2+y^2) の係数がゼロの場合、直線の一般式になるが、ゼロ除算を用いると、それが保証されるばかりか、直線の中心は 原点である、直線も点円も曲率がゼロであることが導かれる。もちろん、ゼロ除算の世界では、全ての直線は原点を通っている。このとき、原点を無限遠点の映った影ともみなせ、原点はこのような意味で もともとの原点とこの意味での点としての、2重性を有し、この概念は今後大きな意味を有することになるだろう。
ゼロ除算1/0=0は ユークリッド幾何学においても、大きな変革を求めている。
以上
上記で、数学的に大事な観点は、ユークリッド自身そうであったが、平行線公理は真理で、証明されるべきもの、幾何学は絶対的な真理であると非ユークリッド幾何学の出現まで、考えられてきたということである。2000年を超える世界観であった事実である。そこで、平行線の公理を証明しようと多くの人が挑戦してきたが、非ユークリッド幾何学の出現まで不可能であった。実は、証明できない命題であったという全く意外な帰結であった。真に新しい、概念、世界観であった。証明できない命題の存在である。それこそ、世界観を変える、驚嘆すべき世界史上の事件であったと言える。
この事件に関してゼロ除算の発見は、全く異なる世界観を明らかにしている。ユークリッドそして、非ユークリッド幾何学の3人の発見者にとって、全く想像ができなかった、新しい事実である。平行線が 無限の先で交わっているとは ユークリッドは考えなかったと思われるが、近代では、無限の先で交わっていると考えられて来ている。― これには、アーベル、オイラー、リーマンなどの考えが存在する。このような考えは、ここ100年以上、世界の常識、定説になっている。ところがゼロ除算では、無限遠点は 数ではゼロが対応していて、平行線は代数的に原点で交わっている、すべての直線は代数的に原点を通っているという解釈が成り立つことを示している。
ユークリッドの幾何学の建設時の想い、ボーヤイ・ヤーノシュの激しい挑戦の様を、 想い を 深く、いろいろ想像している。
以 上
Matrices and Division by Zero z/0 = 0
再生核研究所声明353(2017.2.2) ゼロ除算 記念日
2014.2.2 に 一般の方から100/0 の意味を問われていた頃、偶然に執筆中の論文原稿にそれがゼロとなっているのを発見した。直ぐに結果に驚いて友人にメールしたり、同僚に話した。それ以来、ちょうど3年、相当詳しい記録と経過が記録されている。重要なものは再生核研究所声明として英文と和文で公表されている。最初のものは
再生核研究所声明 148(2014.2.12): 100/0=0, 0/0=0 - 割り算の考えを自然に拡張すると ― 神の意志
で、最新のは
Announcement 352 (2017.2.2): On the third birthday of the division by zero z/0=0
である。
アリストテレス、ブラーマグプタ、ニュートン、オイラー、アインシュタインなどが深く関与する ゼロ除算の神秘的な永い歴史上の発見であるから、その日をゼロ除算記念日として定めて、世界史を進化させる決意の日としたい。ゼロ除算は、ユークリッド幾何学の変更といわゆるリーマン球面の無限遠点の考え方の変更を求めている。― 実際、ゼロ除算の歴史は人類の闘争の歴史と共に 人類の愚かさの象徴であるとしている。
心すべき要点を纏めて置きたい。
1) ゼロの明確な発見と算術の確立者Brahmagupta (598 - 668 ?) は 既にそこで、0/0=0 と定義していたにも関わらず、言わば創業者の深い考察を理解できず、それは間違いであるとして、1300年以上も間違いを繰り返してきた。
2) 予断と偏見、慣習、習慣、思い込み、権威に盲従する人間の精神の弱さ、愚かさを自戒したい。我々は何時もそのように囚われていて、虚像を見ていると 真智を愛する心を大事にして行きたい。絶えず、それは真かと 問うていかなければならない。
3) ピタゴラス派では 無理数の発見をしていたが、なんと、無理数の存在は自分たちの世界観に合わないからという理由で、― その発見は都合が悪いので ― 、弟子を処刑にしてしまったという。真智への愛より、面子、権力争い、勢力争い、利害が大事という人間の浅ましさの典型的な例である。
4) この辺は、2000年以上も前に、既に世の聖人、賢人が諭されてきたのに いまだ人間は生物の本能レベルを越えておらず、愚かな世界史を続けている。人間が人間として生きる意義は 真智への愛にある と言える。
5) いわば創業者の偉大な精神が正確に、上手く伝えられず、ピタゴラス派のような対応をとっているのは、本末転倒で、そのようなことが世に溢れていると警戒していきたい。本来あるべきものが逆になっていて、社会をおかしくしている。
6) ゼロ除算の発見記念日に 繰り返し、人類の愚かさを反省して、明るい世界史を切り拓いて行きたい。
以 上
追記:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告
http://ameblo.jp/syoshinoris/theme-10006253398.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html
再生核研究所声明378 (2017.8.4): マインドコントロール下にあるゼロ除算 ― 強い思い込み
強い教育で異なった考え,対立する見方が受け入れない状況をしばしばマインドコントロールという言葉で表現されている。いくら議論しても分かってもらえない、感性や強い性格の違いとも言える。
ゼロ除算の新しい発見とその反響にそのような印象を強く抱いている。
まずゼロ除算は、代数的にはゼロ除算を含む山田体として、代数的には確定されている。また、十分一般的な状況下で高橋の一意性定理でそれ以外のゼロ除算は有り得ないことが保証されている。しかしながら、具体的な応用や世の中への影響にはゼロ除算算法の考えが大事で、既に広範な具体的な知見が多く挙げられている:
再生核研究所声明 373 (2017.7.17): 高木貞治 「解析概論」の改変構想
再生核研究所声明 374 (2017.7.20):微分方程式論における不完全性と問題
再生核研究所声明 375 (2017.7.21):ブラックホール、ゼロ除算、宇宙論
再生核研究所声明376 (2017.7.31):現代初等数学における間違いと欠落 ― ゼロ除算の観点から
特に世の反響の鈍さを指摘するために、上記のように現代基礎数学の間違いと具体的な影響の大きさを簡潔に触れた。しかるに、ゼロ除算はダメだとの印象を持つ者が未だに多いように感じられる状況が存在する。初期から3年以上を経過しても、見解の相違が全然縮まらない状況が相当数の同侶たちの間にも存在する。そこで、その原因について思いを述べておきたい。
まさか、基礎数学の内容や教育、我々の空間の認識の間違いを指摘されて、そのままに出来る数学者はいないだろうと考える。なぜなら、数学者や先生などは 数学の教育と研究に使命感を持ち、それらに喜びと生きがいを見出し、さらに 義務さえ負う者たちだからである。もっとも真理を追求すべき者が逆にデータなどを捏造している社会現象さえ出ているが、それは不祥事の 世に稀なる現象であると考えたい。多くは自分の研究に集中していて、他のことに関心が行かない 状況が見える。
この状況を真面目に直視すると、超古典的な結果に反する結果で、とても信じられない、数学として正しくても とても受け入れられないと発想して、最初から取り合わない、関心を抱かない、ふれない心境ではないだろうか。― 論文や口頭発表でゼロ除算の内容は単純明快であるにも関わらず、そのような状況は 永い歴史と生い立ちからの世界観を変えられない、強いマインドコントロール下にあるような状況のためではないかと考えられる。
この状況における考察を研究仲間で繰り返し話題にしているが、逆に数学の専門家などが理解しにくく かえって素人やそう深い専門家でない人たちの方が ゼロ除算の結果を受け入れ易いという事実を反映させている。専門家は、自分の専門に入りすぎて、専門以外に興味も関心も抱けない状況が広く見られる ― このような余裕のない状況で、良い研究や教育ができるだろうか と 大いに危惧される。人生とは何かの視点からも問題があるように感じられる。
ゼロ除算は 物理学を始め、広く自然科学や計算機科学への大きな影響があり、さらに哲学、宗教、文化への大きな影響がある。しかしながら、ゼロ除算の研究成果を教科書、学術書に遅滞なく取り入れていくことは、真智への愛、真理の追究の表現であり、四則演算が自由にできないとなれば、数学者ばかりではなく、人類の名誉にも関わることである。実際、ゼロ除算の歴史は 止むことのない闘争の歴史とともに人類の恥ずべき人類の愚かさの象徴となるだろう。世間ではゼロ除算について不適切な情報が溢れていて 今尚奇怪で抽象的な議論によって混乱していると言える。― 美しい世界が拓けているのに、誰がそれを閉ざそうと、隠したいと、無視したいと考えられるだろうか。我々は間違いを含む、不適切な数学を教えていると言える: ― 再生核研究所声明 41: 世界史、大義、評価、神、最後の審判 ―。
地動説のように真実は、実体は既に明らかである。 ― 研究と研究成果の活用の推進を 大きな夢を懐きながら 要請したい。 研究課題は基礎的で関与する分野は広い、いろいろな方の研究・教育活動への参加を求めたい。素人でも数学の研究に参加できる新しい初歩的な数学を沢山含んでいる。ゼロ除算は発展中の世界史上の事件、問題であると言える(再生核研究所声明325(2016.10.14) ゼロ除算の状況について ー 研究・教育活動への参加を求めて)。
人間とはどのようなものかについて、下記も参照:
再生核研究所声明191(2014.12.26) 公理系、基本と人間
― 我々の前提は、大丈夫だろうか。適切であろうか。我々の基礎は適切であろうか。疑い、他の立場は有り得ないであろうか? 基礎の基礎を省察していきたい。それこそが, 真智への愛と言える。
公理系は、変わる可能性があり、いろいろな世界が有り得る。いろいろな公理系を超えて、我々はより自由になり、広い大きな世界を観ることができる。
これは、民族や国家には固有の基礎があり、違えば、違う基礎が有る。人種、性別でも基礎が相当に違い、宗教によっても、学歴や能力、貧富の差や、地域でも基礎について相当な違いが有る。 それらの違い超えて、しっかり背景を捉えて、行こうということを述べている。
さらに言えば、予断、独断、偏見、思い込み、決めつけ、習慣、慣習、それらも時として、省察が必要である。
この声明の背景には 最近のゼロ除算100/0=0,0/0=0の発見がある。 長い間確立されていた定説の変更、新発見である。―
以 上
再生核研究所声明 375 (2017.7.21):ブラックホール、ゼロ除算、宇宙論
本年はブラックホール命名50周年とされていたが、最近、wikipedia で下記のように修正されていた:
名称[編集]
"black hole"という呼び名が定着するまでは、崩壊した星を意味する"collapsar"[1](コラプサー)などと呼ばれていた。光すら脱け出せない縮退星に対して "black hole" という言葉が用いられた最も古い印刷物は、ジャーナリストのアン・ユーイング (Ann Ewing) が1964年1月18日の Science News-Letter の "'Black holes' in space" と題するアメリカ科学振興協会の会合を紹介する記事の中で用いたものである[2][3][4]。一般には、アメリカの物理学者ジョン・ホイーラーが1967年に "black hole" という名称を初めて用いたとされるが[5]、実際にはその年にニューヨークで行われた会議中で聴衆の一人が洩らした言葉をホイーラーが採用して広めたものであり[3]、またホイーラー自身は "black hole" という言葉の考案者であると主張したことはない[3]。https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%A9%E3%83%83%E3%82%AF%E3%83%9B%E3%83%BC%E3%83%AB
世界は広いから、情報が混乱することは よく起きる状況がある。ブラックホールの概念と密接な関係のあるゼロ除算の発見(2014.2.2)については、歴史的な混乱が生じないようにと 詳しい経緯、解説、論文、公表過程など記録するように配慮してきた。
ゼロ除算は簡単で自明であると初期から述べてきたが、問題はそこから生じるゼロ除算算法とその応用であると述べている。しかし、その第1歩で議論は様々でゼロ除算自身についていろいろな説が存在して、ゼロ除算は現在も全体的に混乱していると言える。インターネットなどで参照出来る膨大な情報は、我々の観点では不適当なものばかりであると言える。もちろん学術界ではゼロ除算発見後3年を経過しているものの、古い固定観念に囚われていて、新しい発見は未だ認知されているとは言えない。最近国際会議でも現代数学を破壊するので、認められない等の意見が表明された(再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告)。そこで、初等数学から、500件を超えるゼロ除算の証拠、効用の事実を示して、ゼロ除算は確定していること、ゼロ除算算法の重要性を主張し、基本的な世界を示している。
ゼロ除算について、膨大な歴史、文献は、ゼロ除算が神秘的なこととして、扱われ、それはアインシュタインの言葉に象徴される:
Here, we recall Albert Einstein's words on mathematics:
Blackholes are where God divided by zero.
I don't believe in mathematics.
George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as {\bf the biggest blunder of his life} (Gamow, G., My World Line (Viking, New York). p 44, 1970).
ところが結果は、実に簡明であった:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
しかしながら、ゼロ及びゼロ除算は、結果自体は 驚く程単純であったが、神秘的な新たな世界を覗かせ、ゼロ及びゼロ除算は一層神秘的な対象であることが顕になってきた。ゼロのいろいろな意味も分かってきた。 無限遠点における強力な飛び、ワープ現象とゼロと無限の不思議な関係である。アリストテレス、ユークリッド以来の 空間の認識を変える事件をもたらしている。 ゼロ除算の結果は、数理論ばかりではなく、世界観の変更を要求している。 端的に表現してみよう。 これは宇宙の生成、消滅の様、人生の様をも表しているようである。 点が球としてどんどん大きくなり、球面は限りなく大きくなって行く。 どこまで大きくなっていくかは、 分からない。しかしながら、ゼロ除算はあるところで突然半径はゼロになり、最初の点に帰するというのである。 ゼロから始まってゼロに帰する。 ―― それは人生の様のようではないだろうか。物心なしに始まった人生、経験や知識はどんどん広がって行くが、突然、死によって元に戻る。 人生とはそのようなものではないだろうか。 はじめも終わりも、 途中も分からない。 多くの世の現象はそのようで、 何かが始まり、 どんどん進み、そして、戻る。 例えばソロバンでは、願いましては で計算を始め、最後はご破産で願いましては、で終了する。 我々の宇宙も淀みに浮かぶ泡沫のようなもので、できては壊れ、できては壊れる現象を繰り返しているのではないだろうか。泡沫の上の小さな存在の人間は結局、何も分からず、われ思うゆえにわれあり と自己の存在を確かめる程の能力しか無い存在であると言える。 始めと終わり、過程も ようとして分からない。
ブラックホールとゼロ除算、ゼロ除算の発見とその後の数学の発展を眺めていて、そのような宇宙観、人生観がひとりでに湧いてきて、奇妙に納得のいく気持ちになっている。
以 上
0 件のコメント:
コメントを投稿