「教科書以外の本に出会って、数学が好きになった」数学の楽しさを伝える横山明日希さん
「数学」というと、どうしても小難しいイメージ。
難解な数式を解いて答えを導き出す作業は、想像しただけでも頭に血が登ってしまいそうです。
そんな数学に楽しく触れ合うための活動をしているのが、横山明日希(あすき)さんです。
“数学のお兄さん”横山明日希さん
理系企画プロデューサー。日本お笑い数学協会副理事。
普段の肩書は“数学のお兄さん”。数学大喜利や数学俳句など別分野と交えたイベントを開催し、数学の楽しさをより魅力的に伝える活動をしています。
教科書以外の本と出会って、数学が好きになった

水上
もともと数学が好きだったのでしょうか。

横山
いや、好きでも嫌いでもなかったです。どちらかと言えば得意という程度でした。

水上
それは意外です。数学を好きになったキッカケはなんでしょうか。

横山
キッカケは中学時代に図書室で出会った、数学にまつわる様々な本です。
教科書に載っている数学とは違って、一問一答クイズや「ウミガメのスープ」のような推理ゲームに近い感じの本で、単純に楽しかったです。
一番衝撃だったのは「暗号」という分野の本でした。まず暗号という分野にここまで数学が関係していることも知らなかったので……驚きましたね。
「数学ってこんなに身近なんだ」「授業で扱う内容以外にも数学のジャンルって色々あるんだ」と気づかされました。

水上
数学の新たな側面を、本を通して発見したのですね。

横山
学校の授業だけではわからなかった、数学の世界の広さに感動しましたし、もっと知りたいと思うようになり惹きこまれました。

進路選択の失敗が“数学のお兄さん”を生んだ

水上
数学に魅了され、大学も数学科に進学されましたね。

横山
そうなんです。でも、進路選択は失敗でした。暗号理論を学びたかったのですが、進学した大学は扱っている研究室がなくて。
数学科ならあるだろって、浅はかな考えで選んだのが間違いでした。

水上
それは痛い誤算でしたね。

横山
あとは、数学を研究したいとか突き詰めたいという気持ちは強くなかったと気づいたのも大きいです。
僕は、数学を使って楽しい時間を過ごしたかっただけだと。
大学1年生の1学期で「これは違うかもしれないな」と気づいてしまいました。結局は負けず嫌いだったので大学院までいっちゃったんですけど(笑)

水上
入学してすぐギャップを感じてしまい、その先不安になりそうですが。

横山
でもせっかく入学したし、今できることをしようと思いました。
自分の強みってなんだろうと考えた時に、「若い」「数学が好き」「数学の楽しみを伝えたい」の3つに行き着きました。
この3つを活かせるものとして、教育テレビの歌のお兄さん、体操のお兄さんからヒントを得て“数学のお兄さん”として大学2年生の頃から活動を始めました。

水上
大学生と“数学のお兄さん”の二足のわらじを履いていたのですね。

横山
最初はこれが仕事になるとは思っていなかったので、通学の傍らブログで数学のネタを公開したり、ボランティアで高校生や先生方に話をする感じなのかな、と思っていました。
しかし何年か名乗っていると不思議なもので、講演会の依頼がくるようになったんです。これをもっとコンテンツ化したら面白いんじゃないか、そう考えたのが活動してから5年ほど経った頃でした。

水上
想像以上に長い道のりですね。

横山
そうですね。ただフリーランスでやっていけるほど仕事があったわけではなく……1年半ほどIT企業に就職して「ネットとはなんぞや」というのを学んだあと、その技術を使って自分の情報をネットで効果的に発信するようになりました。
そこから今まで、“数学のお兄さん”としてフリーランスで活動しています。
自分と同じ失敗をしてほしくない

水上
“数学のお兄さん”として活動を続ける原動力はなんでしょうか。

横山
自分自身の原体験として「こういう場所があったらよかったのに」とずっと思っていて。
早い段階で数学の楽しさに気づいていたら、もっと勉強が楽しかっただろうにとか、進路の情報収集を前もってできていれば進路選択のミスも防げたんじゃないかとか。
そういった後悔を誰にもしてほしくないんです。そのために、新しい情報源や新しい情報発信の方法を作り上げていくことが僕の役割だと思っています。

水上
自身の体験をもとに、誰かのために尽力する姿勢がステキです。

横山
数学に限らず、人を助けたいという気持ちがあって、たまたま数学が好きだったから今の活動をしているという感じです。
数学大喜利や数学俳句など、「数学×お笑い」という入りやすい間口を作ることで、これから数学を学びたい人、数学に苦手意識を持っている人のコンプレックスを取り除けたらと思っています。

好きな数字=3

水上
数学に対し熱い思いをもつ横山さん、好きな数字ってありますか。

横山
3です。

水上
すごい、即答ですね(笑)どうして3が好きなんですか。

横山
かけっこや塾のテストで3位になることが多くて、以前から3に縁があるなと思って調べたら、意外と大事な数字ってことに気づきました。
だって、2つの点だと線ですが、3つの点があると三角形ができ、平面が生まれるでしょ。僕達が生きているのも三次元。あとは三種の神器、色の三原色というのもありますし。

水上
言われてみたら確かに、身近に3が溢れていますね。

横山
実は以前好きな数字についてアンケートをしたことがあったのですが、やっぱり3が人気だったんです。
[ご協力願い!]
「最も愛される数字は?」をテーマに自由研究発表をする事になりました。
そこで、「あなたの好きな数字」についてアンケートのご回答と拡散のご協力をお願いしたいです。
回答は2分かからないです。
回答先URL↓https://docs.google.com/forms/d/1IAVLT5ySJgUr86Xp1NvfTzK1ln93Z0EHls08c_lk3bo/viewform …好きな数字とその理由は?
docs.google.com

横山
3を選んだ理由は様々で、例えば「1.2.3とぱっと認識できる最小の単位だから」「形が可愛くて書くたびに楽しいから」「奇数で素数なところがすき」など各々思い入れがあるようです。
「3にまつわるエピソードを話してください」って言ったら、みんな何か1つは持ってるんじゃないですかね。

水上
私は3人兄弟の末っ子(3番目)です。

横山
あ、すごい!持ってますね(笑)
共感できる?数学マニアあるある

水上
数学を愛するマニアならではの“あるある”ってありますか。

横山
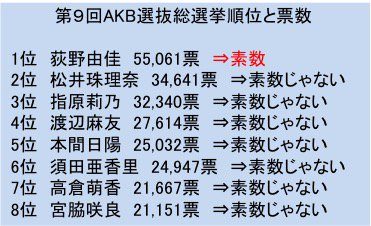
数字を見ると素数かどうか確認しますね。これは絶対します。AKB総選挙の票数も、素数かどうかチェックしていました。

水上
見るところが違う(笑)

横山
あと数式を書くアプリを持ってます。「desmos(デスモス)」ってアプリで、式を入力すると解いたりグラフにしてくれます。

水上
マニアックなアプリですね。今お話を聞かなかったら、一生知ることはなかったかもしれません(笑)彼女といる時に出る、数学マニアならではの行動ってあります?

横山
あ〜、自分では気づいてないかもしれない(笑)でも1から100まで説明しがちですね。物事の成り立ちとか、そもそもの土台から説明しないとしっくりこないです。だから色んな物事は、とことん調べちゃいますね。

水上
知らないことを細かく教えてくれるのは好感度高いですよ!

横山
よかったです。あと記念日を意外と覚えていがち……とか(笑)ただ記念日を覚えていても、前回何をしたかは忘れちゃうんですけどね。
記念日もそうですが、彼女の年齢や指のサイズなど、基本的に数字があったらそれについて解説します。

水上
「数字覚えていがち」と「説明しがち」のダブルコンボですね!

横山
例えば彼女の25歳の誕生日だったら、「25歳になったんだね、25は平方数だね、5×5=25になるね、おめでとうございます。次の平方数は36歳だから、11年後だし、貴重な平方数の年を幸せに過ごしてね」とか言っちゃいますね。

水上
……。(思ったより説明が激しい)
数学を学ぶことがステータスになればいい

水上
今後の活動について教えてください。

横山
「自然と数学」をテーマに、外で体を動かしながら数学に触れ合う機会を作りたいと思っています。そもそも自然の中で文明を発展させていく時に数学は生まれたので、原点回帰ですね。
紙の上を離れて、日常に数学が寄り添うような幅広い活動をしていきたいです。

水上
数学を英会話のように、気軽に学べたらいいのにと思っています。

横山
そうですね。そういった気軽に学べる場所を作ることも大切ですし、数学を学ぶことがステータスになれば、学びたいという意欲を持つ方が増えるのではないかと思います。
そうなるように、頑張って活動を続けていきたいと思います。

横山さんの人柄がにじみ出る、濃い話を聞くことができました。
嫌われがちな数学をもっと好きになってほしい、もっと楽しんでほしいという気持ちがひしひしと伝わってきました。
インタビュー中にあった「数学×お笑い」のイベントを定期的に開催しているので、興味のある方は横山さんの公式サイト、Twitterで情報をご覧ください。https://irorio.jp/kamiiiijo/20170819/413232/
興味あります:
再生核研究所声明334(2016.11.25) 数理科学に興味を懷く方、発見に興味を持つ方 ― お願い
ゼロ除算1/0=0/0=z/0=0は拡張された分数の意味で、数学的に厳密に 確立され 既に自明ですが、物理などに現れる公式において、分数で分母がゼロになるとき、ゼロ除算の結果が自然に成り立っている場合が沢山発見されました。これは、物理学などに現れる分数には このように拡張された意味での分数になっているという意味で、自然を表現する物理学は、賢いと表現できます。― 物理学などで、多くの場合、拡張された意味での分数を表していたということです。― 数学では禁じられたこと、不可能性に最初に遭遇することとされてきた。
そこで、世に現れる多くの公式について、ゼロ除算の結果が成り立っているか、検証、吟味を行いたいと考えて、素人としていろいろ検討を始めていますが、大体200件の具体的な検討を行いました。世に分数で表現される公式は実に多いので、いろいろな方にそれぞれの専門分野や興味ある分野、関心のあるところで、分数におけるゼロ除算の状況を検討して頂ければ誠に幸いです。楽しい現象を発見できれば、大いに楽しめるのではないでしょうか。
具体例について 下記メールにて 連絡して頂ければ幸いです:
kbdmm360@yahoo.co.jp, 再生核研究所
ゼロ除算の注意をして置きます。 分子、分母が独立の時には、上記のように結果が述べられますが、分子、分母に関係がある場合には、いろいろな考え方が有って、結果は一意には一般には定まりませんが、一番有効な考え方は 次のようなゼロ除算算法です:
For any formal Laurent expansion around z=a,
f(z) = \sum_{n=-\infty}^{\infty} C_n (z - a)^n,
we obtain the identity, by the division by zero
f(a) = C_0.
Note that here, there is no problem on any convergence of the expansion at the point z = a. (Here, as convention, we consider 0^0=1.)
We note that:
If a point a is a pole of order n of an analytic function f(z) and we set g(z)=(z - a)^{n}f(z), then
f(a)=\frac{1}{n!}g^{(n)}(a).
We give examples.
If f(z)=\frac{e^{z}}{\left(z-1\right)^{3}}, then g(z) =e^{z} and n=3. So we have
f(1)=\frac{e}{3!}.
If f(z)=\frac{\log z}{\left(z-1\right)^{n}}, where n>1, then g(z) = \log z, and
f(1)=\left(-1\right)^{n-1}\frac{1}{n}.
最も典型的な例は tan 90度が0であることで、大きな影響がある。
以 上
追記:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi
数学基礎学力研究会のホームページ
URLは
http://www.mirun.sctv.jp/~suugaku
○ 堪らなく楽しい数学-ゼロで割ることを考える(28)
ゼロ除算1/0=0/0=z/0=0は拡張された分数の意味で、数学的に厳密に 確立され 既に自明ですが、物理などに現れる公式において、分数で分母がゼロになるとき、ゼロ除算の結果が自然に成り立っている場合が沢山発見されました。これは、物理学などに現れる分数には このように拡張された意味での分数になっているという意味で、自然を表現する物理学は、賢いと表現できます。― 物理学などで、多くの場合、拡張された意味での分数を表していたということです。― 数学では禁じられたこと、不可能性に最初に遭遇することとされてきた。
そこで、世に現れる多くの公式について、ゼロ除算の結果が成り立っているか、検証、吟味を行いたいと考えて、素人としていろいろ検討を始めていますが、大体200件の具体的な検討を行いました。世に分数で表現される公式は実に多いので、いろいろな方にそれぞれの専門分野や興味ある分野、関心のあるところで、分数におけるゼロ除算の状況を検討して頂ければ誠に幸いです。楽しい現象を発見できれば、大いに楽しめるのではないでしょうか。
具体例について 下記メールにて 連絡して頂ければ幸いです:
kbdmm360@yahoo.co.jp, 再生核研究所
ゼロ除算の注意をして置きます。 分子、分母が独立の時には、上記のように結果が述べられますが、分子、分母に関係がある場合には、いろいろな考え方が有って、結果は一意には一般には定まりませんが、一番有効な考え方は 次のようなゼロ除算算法です:
For any formal Laurent expansion around z=a,
f(z) = \sum_{n=-\infty}^{\infty} C_n (z - a)^n,
we obtain the identity, by the division by zero
f(a) = C_0.
Note that here, there is no problem on any convergence of the expansion at the point z = a. (Here, as convention, we consider 0^0=1.)
We note that:
If a point a is a pole of order n of an analytic function f(z) and we set g(z)=(z - a)^{n}f(z), then
f(a)=\frac{1}{n!}g^{(n)}(a).
We give examples.
If f(z)=\frac{e^{z}}{\left(z-1\right)^{3}}, then g(z) =e^{z} and n=3. So we have
f(1)=\frac{e}{3!}.
If f(z)=\frac{\log z}{\left(z-1\right)^{n}}, where n>1, then g(z) = \log z, and
f(1)=\left(-1\right)^{n-1}\frac{1}{n}.
最も典型的な例は tan 90度が0であることで、大きな影響がある。
以 上
追記:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://okmr.yamatoblog.net/division%20by%20zero/announcement%20326-%20the%20divi
数学基礎学力研究会のホームページ
URLは
http://www.mirun.sctv.jp/~suugaku
○ 堪らなく楽しい数学-ゼロで割ることを考える(28)
再生核研究所声明327(2016.10.18) 数学教育についての提案
次で、数学教育の重要性、効用性について触れている:
再生核研究所声明313(2016.08.01) 良い数学教育の推進を
― 数学を通して、人類が交流でき、世には道理、秩序が 存在すると理解できるだろう。分かり易いスポーツを通して、ドラマを見て、芸術を通して理解するは 世に多いが、数学の効用をここでは強調したい。道理、秩序に対する認識には 数学の効用は大きく、上記 公正の原則の理解にも 大きく寄与するのではないだろうか。数学教育の充実を国際的な視点で提案したい。その留意点を纏めて置きたい:
1) 世には共通の論理があることを理解し、論理的な思考を学習する。
2) 数学の論理的な面には、美しさとuniverseの、世の秩序を述べていることを学ぶ。
3) 非ユークリッド幾何学の出現過程を良く学び、真理を追求する精神と感情と論理の関係を学ぶ。批判精神、理性、客観性について学ぶ。予断と偏見、思い込み、囚われやすい人間の精神を掘り下げる。
ここで、数学教育の充実とは、いわゆる数学の学力、問題解決に重点をおいた従来の学習ではなく、上記のような数学教育を通して身に付く数学の精神に重点をおいた教育である。他方数学の学力を付けることに偏りすぎたり、学力を競争させたりして 世に多くの数学嫌いな人たちを育てていることを大いに反省したい。数学の美しさ、楽しさを教えることが第一であると心がけなければならない。
数学愛好者の増大は かつて和算が広く民衆に普及していたように、環境にも優しく、人間の修行にも、精神衛生上も、また創造性を養い、考える力を育成するにも大いに貢献するのではないだろうか。囲碁や将棋、歌会、俳句会など良い趣味集団を構成しているが、数学愛好者クラブなど大いに進められるべきではないだろうか。新聞やテレビ、マスコミ、週刊誌などでもどんどん話題を取り上げ、また奨励されるべきではないだろうか。社会の浄化と低俗化防止にも貢献するのではないだろうか。―
と述べた。古くはプラトン学派の門に、幾何学知らざる者この門をくぐるべからず、ナポレオンが軍隊を強くするには数学の教育が大事であると述べていることや、現中国政府の数学重視の姿勢も注目される。
ここでは、明確な提案が閃いたので纏めて置きたい。まず現状の分析と問題であるが、数学は選別、能力を評価する重要な科目になっていて、受験勉強の強い枠に縛られてカリキュラムは相当に厳格に範囲が定められている。そのため限られた範囲での特訓の要素が強く、現実には理想的な教育の有り様からの乖離が甚だしい状態と言える。標語的には、ゆっくり面白いところを追求しようとすれば、そんなことでは、時間内に解答できない、そのようなものは型として、このように対応すれば良いと、薄っぺらな教育内容になり、多くの場合才能ある学生の みずみずしい知的好奇心 を失なわせ、薄っぺらな学習で数学そのものを嫌う学生を多く育てている現実があると考えられる。これは創造性や好奇心を育てる教育と いわゆる学力をつけるための勉強の乖離の問題である。さらに顕著な事実として、高校までの数学と大学での数学の大きな乖離は 相当に広く認められる現象ではないだろうか。多くの高校生は、大学に入って、数学とはそんなに広く、深く、雄大なものであるかと知って驚くのではないだろうか? また、教育現場の感じも相当に違う感じを受けるだろう。
― このような乖離は、研究成果と学部教育の内容についても言えることに注意しておきたい ―。
背に腹は変えられない、受験勉強は無視できない現実であるから、この問題を改善する具体的な提案として、例えば、週1時間とか、月1時間、カリキュラムにとらわれない数学の時間を用意して、カリキュラムに関係する素材や、新しい話題、面白い歴史的な話題から題材をとり、本来数学の教育に求められるような方向での教育を行うようにする。このような時間は、先生の新鮮な研究、研修にも繋がる面があって 先生の柔軟な精神の涵養にも良いのではないだろうか。さらに視野を広げるためにも、いろいろな講演会の企画なども良いのではないだろうか? 提案したい。数理科学の文化の裾野を広げる努力をしたい。近年は教育・研究環境の厳しさと専門の深さ、困難さで、専門的に深くなりすぎて、数理科学など幅の広さや基礎への関わりが薄くなっているように感じられる。その様な事情を反映させて、教育が疎かになる傾向にもなっているのではないかと危惧される。成果が数字に表されるような貧しい教育である。
数学の教育については、下記も参照:
再生核研究所声明315(2016.08.08) 世界観を大きく変えた、ユークリッドと幾何学
再生核研究所声明283 (2016.2.8) 受験勉強が過熱化した場合の危惧について
再生核研究所声明260 (2015.12.07) 受験勉強、嫌な予感がした ― 受験勉強が過熱化した場合の弊害
再生核研究所声明 187 (2014.12.8)工科系における数学教育について
以 上
再生核研究所声明331(2016.11.04) 提案 ― ゼロ除算の研究は、学部卒論や修士論文の題材に適切
(雨上がり 山間部の散歩で考えが湧いた。ゼロ除算の下記論文は、新しい数学の研究課題で、学部4年生の卒論ゼミの課題、修士論文の研究課題に適切である:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications -Plenary Lectures: Isaac 2015, Macau, China. (Springer Proceedings in Mathematics and Statistics, Vol. 177) Sep. 2016 305 pp. (Springer)
Paper:Division by Zero z/0 = 0 in Euclidean Spaces
Dear Prof. Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
With reference to above, The Editor-in-Chief IJMC (Prof. Haydar Akca) accepted the your paper after getting positive and supporting respond from the reviewer.
Now, we inform you that your paper is accepted for next issue of International Journal of Mathematics and Computation 9 Vol. 28; Issue 1, 2017),
数学基礎学力研究会のホームページ
URLは
簡単に理由を纏めて置きたい。
1) 基礎知識が学部3年生程度で十分で、基本的な結果を議論でき、新しい結果を導ける余地が十分に存在する。新規で、多くの人が興味を持つ課題で国際的にも広く交流できる。
2) 内容は、永い歴史を有する世界史の問題に関わり、空間の考え、勾配、微分、接線、連続性、無限など数学の基礎概念に関与している。相対性理論、ブラックホール、ビッグバン、計算機障害などにも関係している。
3) もともと歴史的な大問題で、ゼロ除算として永い歴史と文化に関わり、広い視点が発展中の生きた数学の中に持てる。
4) 論理には厳格性、精密性、創造性が要求され、数学の精神の涵養に適切である。予断と偏見、思い込みの深さなどについて人間を知ることが出来る。
5) 基礎数学の広範な修正構想に参画でき、物理学など広い研究課題への応用が展望でき、ゼロ除算算法のような新規で基礎数学の新しい手段を身に付けることが出来る。
6) 現在数学は高度化、細分化して、永い学習期間を経て創造的な仕事に取り掛かれるのが普通であるが、ゼロ除算の研究課題では初期段階から、新しい先端の研究に取り掛かれる基礎的な広い研究領域が存在する。ゼロ除算の研究課題は、世にも稀なる夢のある研究課題であると考えられる。― アリストテレス以来、あるいは西暦628年インドにおけるゼロの記録と、算術の確立以来、またアインシュタインの人生最大の懸案の問題とされてきた、ゼロで割る問題 ゼロ除算は、本質的に新しい局面を迎え、数学における初歩的な部分の欠落が明瞭になってきた。ここ70年を越えても教科書や学術書における数学の初歩的な部分の期待される変更は かつて無かった事である。ユークリッドの考えた空間と解析幾何学などで述べられる我々の空間は実は違っていた。いわゆる非ユークリッド空間とも違う空間が現れた。不思議な飛び、ワープ現象が起きている世界である。ゼロと無限の不思議な関係を述べている。これが我々の空間であると考えられる(再生核研究所声明325(2016.10.14) ゼロ除算の状況について ー 研究・教育活動への参加を求めて)。
偉大なる研究は 2段階の発展でなされる という考えによれば、ゼロ除算には何か画期的な発見が大いに期待できるのではないだろうか。 その意味では 天才や超秀才による本格的な研究が期待される。純粋数学として、新しい空間の意義、ワープ現象の解明が、さらには相対性理論との関係、ゼロ除算計算機障害問題の回避など、本質的で重要な問題が存在する。 他方、新しい空間について、ユークリッド幾何学の見直し、世のいろいろな現象におけるゼロ除算の発見など、数学愛好者の趣味の研究にも良いのではないだろうか。 ゼロ除算の研究課題は、理系の多くの人が驚いて楽しめる普遍的な課題で、論文は多くの人に愛される論文と考えられる。
以 上
 横山 明日希 @asunokibou
横山 明日希 @asunokibou
0 件のコメント:
コメントを投稿