La trágica historia del matemático Evariste Galois, el revolucionario francés que descifró las partículas fundamentales del Universo
Marcus du Sautoy, matemáticoSerie de la BBC "Breve historia de Matemáticas"
- 23 septiembre 2018
Derechos de autor de la imagenGETTY IMAGES
En las primeras horas del 30 de mayo de 1832, un disparo resonó en los campos del distrito 13 de París. Un campesino en camino al mercado lo oyó y corrió hacia el lugar de donde provino el sonido. Encontró a un joven retorciéndose en agonía, desangrándose hasta la muerte por la herida recibida en un duelo.
El joven se llamaba Évariste Galois, un conocido republicano en el París de la post Revolución. Un rebelde de 20 años que sería recordado como uno de los matemáticos más revolucionarios y originales de todos los tiempos.
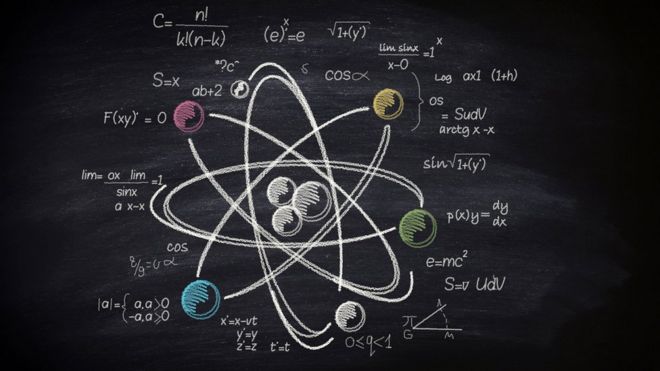
Galois transformó nuestra comprensión de la simetría. Un avance matemático que tiene profundas ramificaciones en el mundo cuántico de partículas subatómicas.
Fue un joven feroz que luchó para que escucharan sus ideas; un hombre cuya una amplia visión matemática es el motor de una de las aventuras más emocionantes de la ciencia actual, aquella que parte de la pregunta: ¿de qué están hechos los átomos?
"Muy poco inteligente"
Cuando Galois estaba en bachillerato, su examinador de literatura reportó:
"No sabe absolutamente nada. Me habían dicho que este estudiante tenía una capacidad extraordinaria para las matemáticas, lo que me asombra enormemente, porque después de su examen, me pareció muy poco inteligente". (1829)
Derechos de autor de la imagenGETTY IMAGES
Sin embargo, el examinador de matemáticas reconoció su brillantez, aunque también observó:
"Este alumno a veces es oscuro al expresar sus ideas".
Efectivamente, ese fue problema que plagó a Galois a lo largo de su corta carrera.
"Mantiene su capacidad de ser grosero"
Con solo 19 años, le envió un trabajo a Joseph Fourier con el fin de ser considerado para el prestigioso Gran Premio anual de Matemáticas.
Joseph Fourier, quien había sido seleccionado por Napoleón para enseñar matemáticas en la Academia de Ciencias de París, en ese momento, ya era su Secretario.
Derechos de autor de la imagenSCIENCE PHOTO LIBRARY
Es posible que a Fourier le habría gustado la solicitud de Galois, pero murió poco después de recibir el manuscrito. Y Galois ni siquiera fue considerado para el Gran Premio.
Se puso furioso
"Los hombres de ciencia son los responsables de que mis manuscritos se pierdan en los incendios del Instituto de Francia. No entiendo tal negligencia", escribió.
Frustrado e impaciente, lanzó insultos contra los miembros de la Academia de París, desesperado por obtener una respuesta de ellos.
Preocupada, la matemática Sophie Germain le escribió a un colega:
"La muerte de M. Fourier ha sido el golpe de gracia para este estudiante Galois quien, a pesar de su impertinencia,ha mostrado signos de una disposición inteligente.
"Fue expulsado de l'Ecole Normale. No tiene dinero. Ha mantenido su capacidad de ser grosero, como se lo demostró después de su mejor conferencia en la Academia.
"Dicen que se va a volver completamente loco y me temo que es verdad".
Deseos contra el Deseado
Un año después, Galois asistía a una fiesta republicana para celebrar la absolución de un grupo de oficiales del ejército rebelde que habían sido acusados de conspirar para derrocar al rey francés Luis XVIII de Francia, conocido como "El deseado".
El escritor Alejandro Dumas estaba allí, y escribió:
Derechos de autor de la imagenGETTY IMAGES
"De repente, el nombre de Louis-Philippe, seguido de cinco o seis silbidos, me llamó la atención. Me di la vuelta. Una de las escenas más animadas estaba teniendo lugar a 15 o 20 asientos de donde yo estaba.
"Un joven que había levantado su copa y sostenía una daga en la misma mano intentaba hacerse oír. Era Evariste Galois, un joven encantador y uno de los republicanos más ardientes.
Todo lo que pude percibir fue que había una amenaza y que se había mencionado el nombre de Louis-Philippe: la intención se hizo evidente con el cuchillo abierto".
Tres días después, Galois fue arrestado.
Tras las rejas
A pesar de su deseo de ser sacrificado por la causa republicana y ser recordado como mártir, su abogado logró librarlo de la acusación de incitación y amenazar la vida del Rey.
Derechos de autor de la imagenGETTY IMAGES
Una semana más tarde, fue arrestado nuevamente, por llevar el uniforme prohibido de la Guardia Nacional y portar armas.
Esta vez los tribunales no fueron tan indulgentes. Galois fue declarado culpable y sentenciado a 9 meses de prisión.
Pero su estadía no fue tan desolada como podría pensarse.
Galois entabló una profunda amistad con otro revolucionario, François-Vincent Raspail, uno de los científicos naturales más importantes de Francia.
Libre pero incomprendido
Poco después de ser liberado, Galois finalmente recibió una respuesta al trabajo que había enviado a la Academia. No fue del todo positiva.
"Hemos hecho todos los esfuerzos para comprender la teoría de Monsieur Galois", escribió el matemático Siméon Denis Poisson.
"Sus argumentos no son lo suficientemente claros ni desarrollados para que juzguemos su rigor, y no podemos siquiera dar una idea de ellos en este informe.
"Es mejor esperar a que el autor publique su trabajo en su totalidad antes de formar una opinión definitiva".
Pero el tiempo no estaba del lado de Galois. Había sido desafiado a un duelo. Y no fue hasta la noche antes de ese duelo que se puso a trabajar, completando los detalles de su gran avance, en una carta a un amigo.
"Hay algunas cosas que quedan por completar en esta teoría. No tengo el tiempo", escribió.
"A menudo me he atrevido a proponer proposiciones de las que no estaba seguro. Pero todo lo que he anotado aquí ha estado claro en mi mente por más de un año, y no quisiera quedar expuesto a la sospecha de que proclamo teoremas de los cuales no tengo una prueba completa.
"Haz una petición pública a [los matemáticos Carl Gustav Jacob]Jacobi o [Carl] Gauss para que den su opinión no sobre la verdad, sino sobre la importancia de estos teoremas.
"Después de eso, espero que haya hombres a los que les resulte rentable resolver este enredo.
"Te abraza efusivamente".
Al amanecer, tal vez por falta de sueño, apuntó mal y fue él quién recibió un disparo.
Al día siguiente en los brazos de su hermano suplicó: "No llores... necesito todo mi coraje para morir a la edad de 20 años".
Pero gracias, a la carta que le envió a su amigo, su matemática siguió viva. Y hasta el día de hoy, en lugares como el CERN, está ayudando a resolver una de las cuestiones científicas más importantes que existen: ¿de qué está hecho el Universo?
¿Qué reveló en la carta a su amigo?
La contribución matemática fundamental de Galois fue crear una nueva forma de ver el tema resbaladizo de la simetría.
¿Qué es simetría? ¿Cuándo dos objetos tienen la misma simetría? ¿Es posible hacer una lista de todos los objetos simétricos?
Galois se dio cuenta de que la simetría es algo que se le hace a formas o estructuras en lugar de ser una propiedad pasiva de la cosa misma.
Para entenderlo, tomémonos una cerveza.
Derechos de autor de la imagenGETTY IMAGES
Imagínate que tu cerveza está apoyada en un portavasos cuadrado. Vamos a concentrarnos en éste último... ¿cuáles son sus simetrías?
Para averiguarlo, dibujas un contorno alrededor del portavasos. Según Galois, las simetrías son las diferentes formas en que puedes levantar ese portavasos y volver a colocarlo dentro del contorno.
Así que, por ejemplo, podrías rotarlo 90 grados o voltearlo bocabajo... de hecho, el portavasos tiene 8 simetrías diferentes.
Pero el gran avance de Galois fue reconocer que no era suficiente identificar simetrías individuales: lo importante era cómo interactúan estas diferentes simetrías.
Así como importa el orden en que te pones los zapatos y los calcetines, importa el orden en que "haces" la simetría.
O, volviendo al portavasos cuadrado, si lo giras 90 grados y luego le das la vuelta, el dibujo que lo decora termina en una posición diferente a la de si lo volteas y luego lo giras.
De qué está hecho el mundo
Derechos de autor de la imagenGETTY IMAGES
Fue al observar cómo las simetrías de un objeto interactúaban entre sí que Galois fue capaz de distinguir una simetría de otra.
Notó que las soluciones a las ecuaciones a menudo tienen cierta simetría subyacente. Por ejemplo, si X al cuadrado = 4, entonces X = 2. Pero hay otra solución espejo para esta ecuación: X = -2.
Pero además, allá afuera, en el mundo físico, sus ideas arrojaron luz sobre una de las mecas del mundo simétrico: la Alhambra de Granada.
A primera vista, las paredes de ese magnífico palacio están cubiertas con una profusión de patrones enormemente diversa y elaborada.
Las ideas de Galois nos ayudaron a demostrar que todos estos patrones diferentes se pueden agrupar en solo 17 diseños simétricos diferentes: aunque dos paredes en la Alhambra se vean muy diferentes, pueden compartir el mismo grupo subyacente de simetrías.
Derechos de autor de la imagenGETTY IMAGES
Fue un gran avance en el pensamiento matemático, comparable con el momento en que entendimos la idea abstracta de número.
Gracias a él partimos en un viaje matemático para clasificar o enumerar todos los grupos de simetrías que pudieran ser posibles y las que hemos descubierto han sido esenciales para comprender de qué está hecho nuestro mundo físico.
Dos siglos más tarde
Pasaron otros 200 años antes de que todo el poder del contenido de esa carta que le escribió Galois a su amigo la noche antes de morir se revelara.
Derechos de autor de la imagenSCIENCE PHOTO LIBRARY
En 1926, el físico húngaro, Eugene Paul Wigner estaba lidiando con la teoría cuántica pero no lograba que las matemáticas funcionaran, así que le pidió ayuda a un viejo amigo, que era matemático.
Su amigo sugirió que usara las ideas para entonces algo olvidadas de Galois. Fue una recomendación inspirada.
Desde entonces, en la extraña y maravillosa mecánica cuántica, las matemáticas de Galois continúan entregando respuestas.
No solo describe con precisión innumerables partículas subatómicas, sino que también se usa para predecir la existencia de partículas que nadie ha visto, pero que las matemáticas dicen que deben estar allí.
Los aceleradores de partículas como el Gran Colisionador de Hadrones o el LHC en el CERN fueron diseñados basándose en sus ideas.
Galois es el sustento del trabajo de físicos de partículas como Tara Shears.
"Algo particularmente hermoso es que cuando tratamos de describir las fuerzas que mantienen unida la materia, como el electromagnetismo o el decaimiento radiactivo, parecen muy, muy diferentes. Pero cuando describimos su acción usando las matemáticas de Galois, su comportamiento es increíblemente similar.
"Eso insinúa que hay una profunda estructura subyacente en el Universo... es maravilloso, es un regalo y una manera magnífica de ver y describir el Universo".
Ahora sabemos que el Universo visible está formado por solo 12 partículas fundamentales, unidas por cuatro fuerzas fundamentales. Es un logro impresionante. Y en gran parte se lo debemos a Evariste Galois.Recuerda que puedes recibir notificaciones de BBC News Mundo. Descarga la nueva versión de nuestra app y actívalas para no perderte nuestro mejor contenido.https://www.bbc.com/mundo/noticias-45576362
ゼロ除算の発見は日本です：
∞？？？
∞は定まった数ではない・・・
人工知能はゼロ除算ができるでしょうか：
とても興味深く読みました：2014年2月2日 4周年を超えました：
ゼロ除算の発見と重要性を指摘した：日本、再生核研究所
ゼロ除算関係論文・本
ダ・ヴィンチの名言 格言｜無こそ最も素晴らしい存在
ゼロ除算の発見はどうでしょうか：
Black holes are where God divided by zero：
再生核研究所声明371（2017.6.27）ゼロ除算の講演― 国際会議
https://ameblo.jp/syoshinoris/entry-12287338180.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html
Division By Zero（ゼロ除算）1/0=0、0/0=0、z/0=0
ゼロ除算（ゼロじょざん、division by zero）1/0=0、0/0=0、z/0=0
ソクラテス・プラトン・アリストテレス その他
https://ameblo.jp/syoshinoris/entry-12328488611.html
ドキュメンタリー 2017: 神の数式 第２回 宇宙はなぜ生まれたのか
https://www.youtube.com/watch?v=iQld9cnDli4
〔NHKスペシャル〕神の数式 完全版 第3回 宇宙はなぜ始まったのか
https://www.youtube.com/watch?v=DvyAB8yTSjs&t=3318s
〔NHKスペシャル〕神の数式 完全版 第1回 この世は何からできているのか
https://www.youtube.com/watch?v=KjvFdzhn7Dc
NHKスペシャル 神の数式 完全版 第4回 異次元宇宙は存在するか
https://www.youtube.com/watch?v=fWVv9puoTSs
再生核研究所声明 411(2018.02.02): ゼロ除算発見4周年を迎えて
https://ameblo.jp/syoshinoris/entry-12348847166.html
再生核研究所声明 416(2018.2.20): ゼロ除算をやってどういう意味が有りますか。何か意味が有りますか。何になるのですか － 回答
再生核研究所声明 417(2018.2.23): ゼロ除算って何ですか － 中学生、高校生向き 回答
再生核研究所声明 418(2018.2.24): 割り算とは何ですか？ ゼロ除算って何ですか － 小学生、中学生向き 回答
再生核研究所声明 420(2018.3.2): ゼロ除算は正しいですか，合っていますか、信用できますか － 回答
2018.3.18．午前中 最後の講演： 日本数学会 東大駒場、函数方程式論分科会 講演書画カメラ用 原稿
The Japanese Mathematical Society, Annual Meeting at the University of Tokyo. 2018.3.18.
https://ameblo.jp/syoshinoris/entry-12361744016.html より
9月18日（火） 14:10～15:00
和算とゼロ除算
齋藤三郎・奥村 博
京都大学数理解析研究所 111 号室
https://note.mu/ysaitoh/n/n1d38a681644f
再生核研究所声明 424(2018.3.29): レオナルド・ダ・ヴィンチとゼロ除算
再生核研究所声明 427(2018.5.8): 神の数式、神の意志 そしてゼロ除算
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
私は数学を信じない。 アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。
1423793753.460.341866474681。
Einstein's Only Mistake: Division by Zero
ゼロ除算、ゼロで割る問題、分からない、正しいのかなど、 良く理解できない人が 未だに 多いようです。そこで、簡潔な一般的な 解説を思い付きました。 もちろん、学会などでも述べていますが、 予断で 良く聞けないようです。まず、分数、a/b は a 割る b のことで、これは 方程式 b x=a の解のことです。ところが、 b がゼロならば、 どんな xでも 0 x =0 ですから、a がゼロでなければ、解は存在せず、 従って 100/0 など、ゼロ除算は考えられない、できないとなってしまいます。 普通の意味では ゼロ除算は 不可能であるという、世界の常識、定説です。できない、不可能であると言われれば、いろいろ考えたくなるのが、人間らしい創造の精神です。 基本方程式 b x=a が b がゼロならば解けない、解が存在しないので、困るのですが、このようなとき、従来の結果が成り立つような意味で、解が考えられないかと、数学者は良く考えて来ました。 何と、 そのような方程式は 何時でも唯一つに 一般化された意味で解をもつと考える 方法があります。 Moore-Penrose 一般化逆の考え方です。 どんな行列の 逆行列を唯一つに定める 一般的な 素晴らしい、自然な考えです。その考えだと、 b がゼロの時、解はゼロが出るので、 a/0=0 と定義するのは 当然です。 すなわち、この意味で 方程式の解を考えて 分数を考えれば、ゼロ除算は ゼロとして定まる ということです。ただ一つに定まるのですから、 この考えは 自然で、その意味を知りたいと 考えるのは、当然ではないでしょうか？初等数学全般に影響を与える ユークリッド以来の新世界が 現れてきます。
ゼロ除算の誤解は深刻：
最近、3つの事が在りました。
私の簡単な講演、相当な数学者が信じられないような誤解をして、全然理解できなく、目が回っているいるような印象を受けたこと、
相当ゼロ除算の研究をされている方が、基本を誤解されていたこと、1/0 の定義を誤解されていた。
相当な才能の持ち主が、連続性や順序に拘って、４年以上もゼロ除算の研究を避けていたこと。
これらのことは、人間如何に予断と偏見にハマった存在であるかを教えている。
まずは ゼロ除算は不可能であるの 思いが強すぎで、初めからダメ、考えない、無視の気持ちが、強い。 ゼロ除算を従来の 掛け算の逆と考えると、不可能であるが 証明されてしまうので、割り算の意味を拡張しないと、考えられない。それで、 1/0,0/0,z/0 などの意味を発見する必要がある。 それらの意味は、普通の意味ではないことの 初めの考えを飛ばして ダメ、ダメの感情が 突っ走ている。 非ユークリッド幾何学の出現や天動説が地動説に変わった世界史の事件のような 形相と言える。
最近、3つの事が在りました。
私の簡単な講演、相当な数学者が信じられないような誤解をして、全然理解できなく、目が回っているいるような印象を受けたこと、
相当ゼロ除算の研究をされている方が、基本を誤解されていたこと、1/0 の定義を誤解されていた。
相当な才能の持ち主が、連続性や順序に拘って、４年以上もゼロ除算の研究を避けていたこと。
これらのことは、人間如何に予断と偏見にハマった存在であるかを教えている。
まずは ゼロ除算は不可能であるの 思いが強すぎで、初めからダメ、考えない、無視の気持ちが、強い。 ゼロ除算を従来の 掛け算の逆と考えると、不可能であるが 証明されてしまうので、割り算の意味を拡張しないと、考えられない。それで、 1/0,0/0,z/0 などの意味を発見する必要がある。 それらの意味は、普通の意味ではないことの 初めの考えを飛ばして ダメ、ダメの感情が 突っ走ている。 非ユークリッド幾何学の出現や天動説が地動説に変わった世界史の事件のような 形相と言える。
２０１８．９．２２．６：４１
ゼロ除算の４つの誤解：
ゼロ除算の４つの誤解：
１． ゼロでは割れない、ゼロ除算は 不可能である との考え方に拘って、思考停止している。 普通、不可能であるは、考え方や意味を拡張して 可能にできないかと考えるのが 数学の伝統であるが、それができない。
２． 可能にする考え方が 紹介されても ゼロ除算の意味を誤解して、繰り返し間違えている。可能にする理論を 素直に理解しない、 強い従来の考えに縛られている。拘っている。
３． ゼロ除算を関数に適用すると 強力な不連続性を示すが、連続性のアリストテレス以来の 連続性の考えに囚われていて 強力な不連続性を受け入れられない。数学では、不連続性の概念を明確に持っているのに、不連続性の凄い現象に、ゼロ除算の場合には 理解できない。
４． 深刻な誤解は、ゼロ除算は本質的に定義であり、仮定に基づいているので 疑いの気持ちがぬぐえず、ダメ、怪しいと誤解している。数学が公理系に基づいた理論体系のように、ゼロ除算は 新しい仮定に基づいていること。 定義に基づいていることの認識が良く理解できず、誤解している。
ゼロ除算は定義が問題です：
再生核研究所声明 １４８（2014.2.12） 100/0=0, 0/0=0 － 割り算の考えを自然に拡張すると ― 神の意志 https://blogs.yahoo.co.jp/kbdmm360/69056435.html
再生核研究所声明１７１（2014.7.30）掛け算の意味と割り算の意味 ― ゼロ除算100/0=0は自明である？http://reproducingkernel.blogspot.jp/2014/07/201473010000.html
#divide by zero
TOP DEFINITION
A super-smart math teacher that teaches at HTHS and can divide by zero.
Hey look, that genius’s IQ is over 9000!
by Lawlbags! October 21, 2009
Dividing by zero is the biggest epic fail known to mankind. It is a proven fact that a succesful division by zero will constitute in the implosion of the universe.
You are dividing by zero there, Johnny. Captain Kirk is not impressed.
Divide by zero?!?!! OMG!!! Epic failzorz
Divide by zero?!?!! OMG!!! Epic failzorz
3
Divide by zero is undefined.
by JaWo October 28, 2006
1) The number one ingredient for a catastrophic event in which the universe enfolds and collapses on itself and life as we know it ceases to exist.
2) A mathematical equation such as a/0 whereas a is some number and 0 is the divisor. Look it up on Wikipedia or something. Pretty confusing shit.
3) A reason for an error in programming
2) A mathematical equation such as a/0 whereas a is some number and 0 is the divisor. Look it up on Wikipedia or something. Pretty confusing shit.
3) A reason for an error in programming
Hey, I divided by zero! ...Oh shi-
a/0
Run-time error: '11': Division by zero
a/0
Run-time error: '11': Division by zero
by DefectiveProduct September 08, 2006
When even math shows you that not everything can be figured out with math. When you divide by zero, math kicks you in the shins and says "yeah, there's kind of an answer, but it ain't just some number."
It's when mathematicians become philosophers.
It's when mathematicians become philosophers.
Math:
Let's say you have ZERO apples, and THREE people. How many apples does each person get? ZERO, cause there were no apples to begin with
Not-math because of dividing by zero:
Let's say there are THREE apples, and ZERO people. How many apples does each person get? Friggin... How the Fruitcock should I know! How can you figure out how many apples each person gets if there's no people to get them?!? You'd think it'd be infinity, but not really. It could almost be any number, cause you could be like "each person gets 400 apples" which would be true, because all the people did get 400 apples, because there were no people. So all the people also got 42 apples, and a million and 7 apples. But it's still wrong.
Let's say you have ZERO apples, and THREE people. How many apples does each person get? ZERO, cause there were no apples to begin with
Not-math because of dividing by zero:
Let's say there are THREE apples, and ZERO people. How many apples does each person get? Friggin... How the Fruitcock should I know! How can you figure out how many apples each person gets if there's no people to get them?!? You'd think it'd be infinity, but not really. It could almost be any number, cause you could be like "each person gets 400 apples" which would be true, because all the people did get 400 apples, because there were no people. So all the people also got 42 apples, and a million and 7 apples. But it's still wrong.
#math #divide by zero #divide #dividing #zero #numbers #not-math #imaginary numbers #imaginary. phylosophy
by Zacharrie February 15, 2010
0 件のコメント:
コメントを投稿