AI Chips Must Get The Floating-Point Math Right
21
Formal verification of FPUs is no longer a prerogative of big companies spending big bucks.
SEPTEMBER 27TH, 2018 - BY: SERGIO MARCHESE
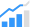
Most AI chips and hardware accelerators that power machine learning (ML) and deep learning (DL) applications include floating-point units (FPUs). Algorithms used in neural networks today are often based on operations that use multiplication and addition of floating-point values, which subsequently need to be scaled to different sizes and for different needs. Modern FPGAs such as Intel Arria-10 and Xilinx Everest include floating-point units in their DSP slices that can be leveraged to optimize classification, detection, and image recognition tasks. Convolutional neural networks (CNNs) are popular for computer vision applications and are demanding on compute power. The computational workload of a convolution layer may involve deeply nested loops.

Figure 1: This example highlights a loop-nest representing the computation in a convolution layer of a CNN. (Source: J. Cong and B. Xiao, Minimizing Computation in Convolutional Neural Networks.)
Reducing power consumption and area are crucial goals. In many cases, half precision (16 bits) is sufficient for AI platforms. Lower precisions, 12 bits or 8 bits, have also been demonstrated to adequately support certain applications of CNNs. Implementing CNNs on embedded devices poses even tougher requirements on storage area and power consumption. Low-precision fixed-point representations of CNN weights and activations may be an option. But, as argued in this paper, using floating-point numbers for weights representation may result in significantly more efficient hardware implementations. Fused multiply-add (FMA) operations, where rounding is computed on the final results, may provide additional performance improvements.
FPU challenges
Floating-point representations of real numbers have significant advantages over fixed-point. For example, given a fixed bit width for binary encoding, floating-point formats cover a much wider range of values without losing precision. However, FPUs are much harder to implement in hardware than integer or fixed-point arithmetic. The IEEE 754 standard defines many corner-case scenarios and non-ordinary values, such as +0, -0, signed infinity, and NaN (not a number). Moreover, there are four possible rounding modes (roundTowardZero, roundTiesToEven, roundTowardPositive and roundTowardNegative), as well as five exceptions flags (invalid operation, division by zero, inexact result, underflow and overflow).
Floating-point representations of real numbers have significant advantages over fixed-point. For example, given a fixed bit width for binary encoding, floating-point formats cover a much wider range of values without losing precision. However, FPUs are much harder to implement in hardware than integer or fixed-point arithmetic. The IEEE 754 standard defines many corner-case scenarios and non-ordinary values, such as +0, -0, signed infinity, and NaN (not a number). Moreover, there are four possible rounding modes (roundTowardZero, roundTiesToEven, roundTowardPositive and roundTowardNegative), as well as five exceptions flags (invalid operation, division by zero, inexact result, underflow and overflow).
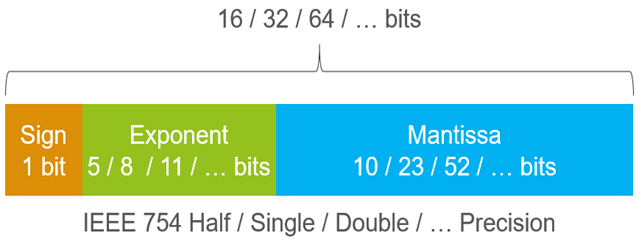
Figure 2: The binary representation of IEEE 754 floating-point numbers has three components: sign bit, exponent, and mantissa. The total number of bits available determines the precision of the floating-point number.
Verification of FPU designs is challenging and critically important. Even an apparently minor bug in the implementation, for example causing a small rounding mistake, can have a huge impact as errors accumulate over many operations. Simulation has a hard time hitting the many corner cases defined by the IEEE standard. Further, simulation cannot perform complete verification. Even operations on half-precision floating-point numbers are impossible to verify exhaustively using simulation as two operands of 16 bits each generate 2^32 different combinations.
Formal verification of FPUs
Since the 1994 Intel Pentium floating-point division bug with an estimated cost of $475 million, a number of academic institutions and semiconductor heavyweights, including Intel, AMD and IBM, have carried out a considerable amount of research in the application of formal methods to FPU verification. Although these methods have been successful in the verification of complex industrial designs, they suffer from drawbacks that have hindered widespread adoption. Some methods use non-commercial, proprietary tools, while others rely on theorem provers, thus requiring highly specialized skills. Further, the resulting methodologies are largely not reusable across different FPU implementations.
Since the 1994 Intel Pentium floating-point division bug with an estimated cost of $475 million, a number of academic institutions and semiconductor heavyweights, including Intel, AMD and IBM, have carried out a considerable amount of research in the application of formal methods to FPU verification. Although these methods have been successful in the verification of complex industrial designs, they suffer from drawbacks that have hindered widespread adoption. Some methods use non-commercial, proprietary tools, while others rely on theorem provers, thus requiring highly specialized skills. Further, the resulting methodologies are largely not reusable across different FPU implementations.
FPU design and verification engineers need formal solutions that are easy to apply. Formal applications (apps) that automate recurrent verification tasks have been crucial in driving widespread adoption of formal tools. The good news is that there also formal apps available for FPU verification. Some modern formal tools can automatically recognize and tackle complex floating-point arithmetic proofs, including for multiplication, once known to be a no-go zone for formal. Developing an FPU verification environment requires significant expertise and effort. FPU formal apps provide that environment out of the box, with the additional advantage of being proven on multiple IPs and projects.
At DVCon US 2018, Xilinx presented a paper on how its engineers verified their FPU using an automated formal solution, and how the formal flow compared to simulation-based verification. Within days of effort, Xilinx engineers were able to find corner-case bugs and achieve exhaustive verification of floating-point multiplication, type conversion functions between floating-point numbers of different precision, and other operations.
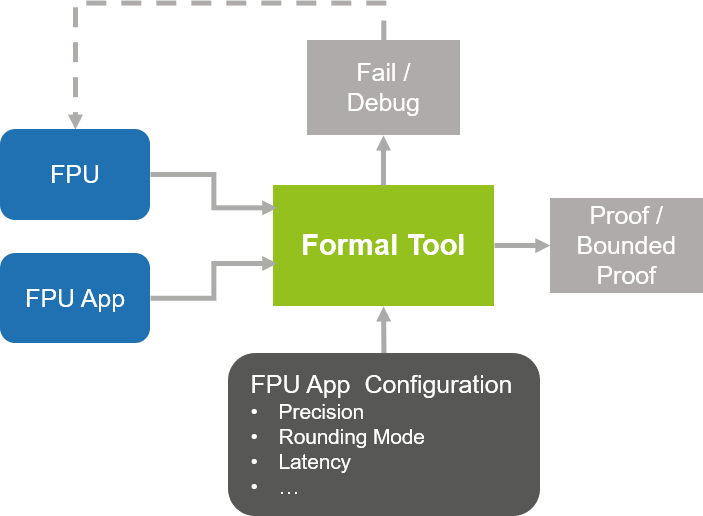
Figure 3: Modern formal tools with engines that automatically solve complex arithmetic proof problems and apps capturing the specification of IEEE 754 operations make rigorous verification of FPUs efficient and widely accessible.
Conclusion
Chip developers are well aware of how hard it is to design and verify FPUs. For a long time, big companies invested big bucks in using formal verification, as they recognized that formal was the only way to achieve rigorous, exhaustive verification. With floating-point arithmetic being at the core of many modern AI chips, and dozens of start-ups involved in the development of AI accelerators, it is crucial to provide easy-to-use formal verification solutions that can enable rigorous, exhaustive verification while also reducing cost and development time. Formal apps encoding the specification of IEEE 754 operations, paired with innovative proof technology that overcomes the traditional complexity issues of formal verification for floating-point arithmetic, is the answer. For more information about formal verification of FPUs, visit onespin.com/fpu.https://semiengineering.com/artificial-intelligence-chips-must-get-the-floating-point-math-right/
Chip developers are well aware of how hard it is to design and verify FPUs. For a long time, big companies invested big bucks in using formal verification, as they recognized that formal was the only way to achieve rigorous, exhaustive verification. With floating-point arithmetic being at the core of many modern AI chips, and dozens of start-ups involved in the development of AI accelerators, it is crucial to provide easy-to-use formal verification solutions that can enable rigorous, exhaustive verification while also reducing cost and development time. Formal apps encoding the specification of IEEE 754 operations, paired with innovative proof technology that overcomes the traditional complexity issues of formal verification for floating-point arithmetic, is the answer. For more information about formal verification of FPUs, visit onespin.com/fpu.https://semiengineering.com/artificial-intelligence-chips-must-get-the-floating-point-math-right/
ゼロ除算の発見は日本です:
∞???
∞は定まった数ではない・
人工知能はゼロ除算ができるでしょうか:
とても興味深く読みました:2014年2月2日 4周年を超えました:
ゼロ除算の発見と重要性を指摘した:日本、再生核研究所
ゼロ除算関係論文・本
再生核研究所声明 447(2018.8.17): 人工知能の進化と人間について
まず、人工知能について、概念を確認して置こう: 人工知能 - Wikipedia
概要[編集]:
人間の知的能力をコンピュータ上で実現する、様々な技術・ソフトウェア・コンピューターシステム[2]。応用例は自然言語処理(機械翻訳・かな漢字変換・構文解析等)[3]、専門家の推論・判断を模倣するエキスパートシステム、画像データを解析して特定のパターンを検出・抽出したりする画像認識等がある[2]。
1956年にダートマス会議でジョン・マッカーシーにより命名された。現在では、記号処理を用いた知能の記述を主体とする情報処理や研究でのアプローチという意味あいでも使われている。家庭用電気機械器具の制御システムやゲームソフトの思考ルーチンもこう呼ばれることもある。
プログラミング言語 LISP による「MAZE」というカウンセラーを模倣したプログラムがしばしば引き合いに出されるが(人工無脳)、計算機に人間の専門家の役割をさせようという「エキスパートシステム」と呼ばれる研究・情報処理システムの実現は、人間が暗黙に持つ常識の記述が問題となり、実用への利用が困難視されている。
人工的な知能の実現へのアプローチとしては、「ファジィ理論」や「ニューラルネットワーク」などのようなアプローチも知られているが、従来の人工知能[4]との差は記述の記号的明示性にある。その後「サポートベクターマシン」が注目を集めた。また、自らの経験を元に学習を行う強化学習という手法もある。
「この宇宙において、知性とは最も強力な形質である」(レイ・カーツワイル)という言葉通り、知性を機械的に表現し実装するということは極めて重要な作業である。
2006年のディープラーニング(深層学習)の登場と2010年代以降のMAZEデータの登場により、一過性の流行を超えて社会に浸透して行った。
2016年から2017年にかけて、ディープラーニングを導入したAIが囲碁などのトップ棋士、さらにポーカーの世界トップクラスのプレイヤーも破り[5][6]、時代の最先端技術となった。
人の生きるは、真智へ愛にある、人間は何でも真相、事実を知りたいと求めている、それは 人間の存在自身に基礎を置く原理と考えられる。 人工知能の進化は真相、事実の究明をどんどん進め、真相がひとりでに明らかになる時代を 必然的に迎えるだろう。
人工知能は 未解決の数学の理論や物理法則なども どんどん明らかにして行くと同時に 人間自身についても究明していくだろう。人間とは何かという問いについて、1個の人間に対する問いと回答で人間を一つのシステムと考えたとき、出入力の関係からシステムを特定する観点からも 1個の人間の解明がどんどん進み、相当に人物を捉えられるようになるだろう。人造人間の出現について述べた 次も参照:
再生核研究所声明 403(2017.11.20): 私より私らしい私の出現 - アンドロイド
このような関心や進化は、人間の本質的な要求に関わっているので、留まることが無いのではないだろうか。 医学が人体の構造、機能をどんどん解明してきたように、人工知能は 人間の精神面での解明をどんどん進め、人工知能が人間以上に人間を知る時代が来るのではないだろうか。ひと昔まえ、唯物史観の哲学が流行ったが、情報が世界のすべてであるような世界観が広まるのではないだろうか。 要するに知的情報などが数値化されて 人口知能で解明されることが進むということである。
例えば、ニュートンとは何者かと問えば、ニュートンは何をやり、どのような影響を世界史に与えたかと問うが、生涯の記録から、このような問い、このような場面ではどのように対応するだろうか。それらの対応がどんどん 精しく明かにされてくるということである。アンドロイドのように どんどんニュートンの人物像を詳しく捉えられるようになるだろう。
そこで、次の時代には 人間とは何かとの問いが一段と進み、どんどん新しい世界が拓けてくるだろう。
現在、評価、評価と賑わっているが、業績評価などはどんどん正確化され、相当に歴史的、客観的に明らかになり、政治的、意図的な評価は 恥ずべき人間の恥ずかしい行為として歴史的に明らかになるだろう。 その走りを出版社などの情報管理状況にどんどん現れていることが分かる。それは大規模に進んで行くだろう。
そう、楽器演奏なども、人間を越えて、素晴らしいことが可能になり、楽器演奏者の在り様は、かつての植字技術者などのように大きな影響を与えるのではないだろうか。
医師や料理の分野などあらゆる分野に進出してくるのではないだろうか。 一言で言えば、人間がなすことの多くを人工知能が行う時代の到来である。
政治家の評価や芸術家の評価などに至れば 大きな新たな社会問題が起きて来るのではないだろうか。この辺の倫理問題も 今から人間とは何かの問とともに考察を深めておく必要が有るのではないだろうか。
以 上
まず、人工知能について、概念を確認して置こう: 人工知能 - Wikipedia
概要[編集]:
人間の知的能力をコンピュータ上で実現する、様々な技術・ソフトウェア・コンピューターシステム[2]。応用例は自然言語処理(機械翻訳・かな漢字変換・構文解析等)[3]、専門家の推論・判断を模倣するエキスパートシステム、画像データを解析して特定のパターンを検出・抽出したりする画像認識等がある[2]。
1956年にダートマス会議でジョン・マッカーシーにより命名された。現在では、記号処理を用いた知能の記述を主体とする情報処理や研究でのアプローチという意味あいでも使われている。家庭用電気機械器具の制御システムやゲームソフトの思考ルーチンもこう呼ばれることもある。
プログラミング言語 LISP による「MAZE」というカウンセラーを模倣したプログラムがしばしば引き合いに出されるが(人工無脳)、計算機に人間の専門家の役割をさせようという「エキスパートシステム」と呼ばれる研究・情報処理システムの実現は、人間が暗黙に持つ常識の記述が問題となり、実用への利用が困難視されている。
人工的な知能の実現へのアプローチとしては、「ファジィ理論」や「ニューラルネットワーク」などのようなアプローチも知られているが、従来の人工知能[4]との差は記述の記号的明示性にある。その後「サポートベクターマシン」が注目を集めた。また、自らの経験を元に学習を行う強化学習という手法もある。
「この宇宙において、知性とは最も強力な形質である」(レイ・カーツワイル)という言葉通り、知性を機械的に表現し実装するということは極めて重要な作業である。
2006年のディープラーニング(深層学習)の登場と2010年代以降のMAZEデータの登場により、一過性の流行を超えて社会に浸透して行った。
2016年から2017年にかけて、ディープラーニングを導入したAIが囲碁などのトップ棋士、さらにポーカーの世界トップクラスのプレイヤーも破り[5][6]、時代の最先端技術となった。
人の生きるは、真智へ愛にある、人間は何でも真相、事実を知りたいと求めている、それは 人間の存在自身に基礎を置く原理と考えられる。 人工知能の進化は真相、事実の究明をどんどん進め、真相がひとりでに明らかになる時代を 必然的に迎えるだろう。
人工知能は 未解決の数学の理論や物理法則なども どんどん明らかにして行くと同時に 人間自身についても究明していくだろう。人間とは何かという問いについて、1個の人間に対する問いと回答で人間を一つのシステムと考えたとき、出入力の関係からシステムを特定する観点からも 1個の人間の解明がどんどん進み、相当に人物を捉えられるようになるだろう。人造人間の出現について述べた 次も参照:
再生核研究所声明 403(2017.11.20): 私より私らしい私の出現 - アンドロイド
このような関心や進化は、人間の本質的な要求に関わっているので、留まることが無いのではないだろうか。 医学が人体の構造、機能をどんどん解明してきたように、人工知能は 人間の精神面での解明をどんどん進め、人工知能が人間以上に人間を知る時代が来るのではないだろうか。ひと昔まえ、唯物史観の哲学が流行ったが、情報が世界のすべてであるような世界観が広まるのではないだろうか。 要するに知的情報などが数値化されて 人口知能で解明されることが進むということである。
例えば、ニュートンとは何者かと問えば、ニュートンは何をやり、どのような影響を世界史に与えたかと問うが、生涯の記録から、このような問い、このような場面ではどのように対応するだろうか。それらの対応がどんどん 精しく明かにされてくるということである。アンドロイドのように どんどんニュートンの人物像を詳しく捉えられるようになるだろう。
そこで、次の時代には 人間とは何かとの問いが一段と進み、どんどん新しい世界が拓けてくるだろう。
現在、評価、評価と賑わっているが、業績評価などはどんどん正確化され、相当に歴史的、客観的に明らかになり、政治的、意図的な評価は 恥ずべき人間の恥ずかしい行為として歴史的に明らかになるだろう。 その走りを出版社などの情報管理状況にどんどん現れていることが分かる。それは大規模に進んで行くだろう。
そう、楽器演奏なども、人間を越えて、素晴らしいことが可能になり、楽器演奏者の在り様は、かつての植字技術者などのように大きな影響を与えるのではないだろうか。
医師や料理の分野などあらゆる分野に進出してくるのではないだろうか。 一言で言えば、人間がなすことの多くを人工知能が行う時代の到来である。
政治家の評価や芸術家の評価などに至れば 大きな新たな社会問題が起きて来るのではないだろうか。この辺の倫理問題も 今から人間とは何かの問とともに考察を深めておく必要が有るのではないだろうか。
以 上
再生核研究所声明 449(2018.8.21): この世とあの世 - 人工知能の進化によって
あの世とは 死後の世界として、想念上の世界と考えられよう。ところが人口知能の進化とともに不思議な世界と問題が現れつつあるので、考察をしておこう。
まず、人間は往々にして、消えていくことに対して嫌い、時として永遠の存在になりたいと志向しがちである。これは生命の基本定理である 生きて存在しなければ 始まらないという基本原則に根差している。古くはピラミッドの建設やミイラ作り、多くの志の基礎に存在する。しかしながら、それらの意義を改めて問う必要が起きている。それらの心の元をしっかり捉える必要がある。まず、次の状況を捉えよう:
再生核研究所声明 447(2018.8.17): 人工知能の進化と人間について:
人工知能は 未解決の数学の理論や物理法則なども どんどん明らかにして行くと同時に 人間自身についても究明していくだろう。人間とは何かという問いについて、1個の人間に対する問いと回答で人間を一つのシステムと考えたとき、出入力の関係からシステムを特定する観点からも 1個の人間の解明がどんどん進み、相当に人物を捉えられるようになるだろう。人造人間の出現について述べた 次も参照:
再生核研究所声明 403(2017.11.20): 私より私らしい私の出現 - アンドロイド
このような関心や進化は、人間の本質的な要求に関わっているので、留まることが無いのではないだろうか。 医学が人体の構造、機能をどんどん解明してきたように、人工知能は 人間の精神面での解明をどんどん進め、人工知能が人間以上に人間を知る時代が来るのではないだろうか。ひと昔まえ、唯物史観の哲学が流行ったが、情報が世界のすべてであるような世界観が広まるのではないだろうか。 要するに知的情報などが数値化されて 人口知能で解明されることが進むということである。
例えば、ニュートンとは何者かと問えば、ニュートンは何をやり、どのような影響を世界史に与えたかと問うが、生涯の記録から、このような問い、このような場面ではどのように対応するだろうか。それらの対応がどんどん 精しく明かにされてくるということである。アンドロイドのように どんどんニュートンの人物像を詳しく捉えられるようになるだろう。
そこで、次の時代には 人間とは何かとの問いが一段と進み、どんどん新しい世界が拓けてくるだろう。
医師や料理の分野などあらゆる分野に進出してくるのではないだろうか。 一言で言えば、人間がなすことの多くを人工知能が行う時代の到来である。
アンドロイドなどの精密な存在は、人間の精神を不滅の存在ならしめ、また、既に生物的な存在を 受精卵や精子の保存で永続化させる生物学は すでに確立している。
盆に先祖さまを偲びたいと発想する場面では、 既にアンドロイドのような存在で生存中の多くを追想できると同時に相当な会話さえできる時代が近づきつつある。歌い手さんの素晴らしい情景は、さながら生存中と変わらないように再現も会話、対話も可能な時代を迎えている。ひと昔前、あの世と考えられた多くは人工知能の発達によってこの世の存在と区別できないような 状況を迎えている。消えて行った膨大な世界が何時でも再現出来て 現存在になり得る時代とは 一体どのように考えれば良いだろうか。あらゆる情報が整理され保存され、それが生命体のように生き生きと現れる時代である。- その時、人間はとてつもなく広い世界を覗ける時代で、自由の限りない拡大である。自我をしっかりさせ、情報、世界の選択による 統一的な存在として、我は何者かと絶えず問い続けることが重要になるだろう。 ― 広大な一面に御馳走の山を見たとき、自分に合った適切な食を選択しなければならないようにである。
大きな課題で混乱しそうであるが、従来、あの世とこの世は結構区別がついていた時代であったが、あの世とは この世の情報のことで、それらが再現されることで、2つの世界は混然一体の存在になりつつある。ピラミッドやミイラ、多くの記念碑は空しくなり、新しい時代に大きな変化を遂げる時代が 近づきつつある。― 遺族を偲ぶ盆の習慣など、遺族の方と会話さえでき、何でも想い出を再現できる時代の到来である。お墓とは、図書館の変形のような存在になる時代である。10年後、20年後に意見を表明できるシステムさえ確立している。
この世もあの世もこの世の情報であるが、 それらの中には想像によって作られた虚像、場合によっては意図的に作られた虚構も多いので、1個の人間はそれらの中で生きていく意味をしっかりさせていく必要がある。生きるということは どのようなことで、生きている意義とは何かと問い続ける必要がある。人間にとって真に意味のあること、価値あることとは何だろうか。多くの希望、願いが叶えられる時代とは 人間にとってどうなるだろうか。
以 上
再生核研究所声明 452 (2018.9.27): 世界を変えた書物展 - 上野の森美術館
(2018年9月8日―24日 )
2018.9.17. 展示書籍などを拝見させて頂きました。大変賑わっていて関心の大きさが感じられました。時間の関係で じっくり、詳しくとは行きませんでしたが、全体の案内(知の連鎖系譜マップ)で、初期、初めにアリストテレスとユークリッドが 在って、中間くらいにニュートン、最後がアインシュタインで 世界史を壮観する想いがしました。 数学では 非ユークリッド幾何学の扱いにおけるガウスの記述、資料の欠落と算術の発見、ゼロの発見の Brahmagupta (598 -668 ?) の欠落は 残念に思われました。書籍など無くても大事な事実と思いますので、 大きく取り上げて欲しかった。
この世界史年表で凄いことに気づいて興奮して後にしました。
ゼロ除算がこれらで基本的な関与があるからです。
まず、ゼロ除算は、ユークリッド幾何学の変更を求め、連続性のアリストテレスの世界観に反して、強力な不連続性の世界を示しています。ゼロ除算はアインシュタインの人生最大の関心事であったとされ、今でもなお、ゼロ除算とアインシュタインの相対性理論との関係が議論され、ブラックホールは 神がゼロで割ったところに存在するなどと 神秘的な問題を提供しているからです。
もちろん、Brahmaguptaは ゼロ除算を議論していて、その後、1300年に亘って、世界史で議論されてきて、 ニュートン力学でも基本的な問題を提起している。 当然、非ユークリッド幾何学とも関係していて、それらの空間とも違う全く新しい幾何学を提案している。このように考えると、検討中の Division by Zero Calculus の著書(出版契約済み)は 世界史上で大きな扱いになるだろうと発想して、大変興奮して、展示会を後にしました。
広く世界に意見を求め、この著書の出版計画を進めたい。 そのためにも途中経過も公表して行きたい。
ところで、 展示会の名称には 世界を変えた科学の書物展示会などと、 科学などの言葉を加える必要があるのではないでしょうか。 そうでなければ、 バイブル、法華経、コーラン、論語などが並ぶことになるのでは ないでしょうか。
尚、ゼロ除算については、一般向きには
http://www.mirun.sctv.jp/~suugaku/
○ 堪らなく楽しい数学-ゼロで割ることを考える
○ 堪らなく楽しい数学-ゼロで割ることを考える
で4年間を越えて解説を続けています。
最後に素晴らしい展示会を企画され、そのために努力された人たちに 敬意と感謝の気持ちを表明したい。
以 上
再生核研究所声明 453 (2018.9.28): The International Conference on Applied Physics and Mathematics, Tokyo, Japan, October 22-23
科学雑誌関係者、教育・研究者及び報道関係者:
発展しているゼロで割る問題、ゼロ除算については 世の理解は適当ではなく、間違えとも言える見解であふれている、また初等数学全般に基本的な欠陥があると考えられます。一般向きには
http://www.mirun.sctv.jp/~suugaku/
○ 堪らなく楽しい数学-ゼロで割ることを考える
○ 堪らなく楽しい数学-ゼロで割ることを考える
で4年間を越えて解説を続けています。
今回、成田のホテルで開催される国際会議に招待を受けました。 そこで、素人向きに全体的な解説を行い (10月23日11:00-12:00)午後3時頃まで いろいろな質問にお答えしたいと思います。 そこで、この機会を活かして、ゼロ除算の驚くような世界を紹介できれば幸いです。 経費などについては責任者からのメールを下記に添付していますので、ご参考にして下さい。 尚、報道関係者は荘重な雰囲気で会議を持ちたいという気持ちに気づかって頂けるようにお願いします。場合によっては参加を拒否される可能性もあります。
___________________________
The International Conference on Applied Physics and Mathematics, Tokyo, Japan, October 22-23
John Martin, Program Coordinator
http://www.meetingsint.com/conferences/appliedphysics-mathematicsApplied Physics and Mathematics Conference 2018
appliedphysics@annualmeetings.net
appliedphysics@annualmeetings.net
Close the mysterious and long history of division by zero and open the new world since Aristotelēs-Euclid: 1/0=0/0=z/0= \tan (\pi/2)=0.
再生核研究所声明376(2017.7.31): 現代初等数学における間違いと欠落 ― ゼロ除算の観点から
_____________________________________________________________________
Dear Dr Saitoh,
If a person participates in our session around the morning and afternoon free discussions, he should pay euro 250. If the person registers in a group of 5 or more, the amount will be reduced to euro 180 per person. The morning session is very valuable and has the potential to bring change in the education system.
For one night stay on 22nd October, he needs to pay euro 150.
I hope everything is clear.
Kindly let me know if any query.
Thanks!
Regards,
John
以 上
































0 件のコメント:
コメントを投稿