2018年6月28日木曜日

The Division by Zero 2018年06月28日(木)NEW ! テーマ：数学 The Division by Zero

The Division by Zero

NEW !
テーマ：

The Division by Zero

Any number divided by zero is undefined — this is perhaps one of the most ubiquitously known mathematical facts. The impossibility of a division by zero has captured the public’s imagination as an aspect of mathematics which is enigmatic, incomprehensible, almost Lovecraftian. However, the division by zero is well within the realms of possibility. For reasons which will be discussed, mathematicians simply chose to not define divisions by zero. Furthermore, division by infinitesimals (numbers infinitely close to zero in value) is not only mathematically possible, but can also give meaningful results.
When mathematicians state that the division by zero is undefined, they mean it literally. Dividing by zero is analogous to drawing a square in a game of tic-tac-toe — a scenario where the results are undefined simply because there are no rules governing such an outlandish input. While arithmetic pre-dates the Common Era, it was not till the 19th century that mathematicians like Grassmann, Dedekind and Peano used formal logic to create “rules”, commonly known as “axioms”, to govern arithmetic. Arithmetic properties, such as the distributive property of multiplication, can be formally derived from Grassmann’s work and the Dedekind–Peano axioms. These mathematicians defined operations like addition and multiplication (and as a corollary, subtraction and division) recursively for the natural numbers , while other mathematicians extended these concepts to other number sets. By the recursive definition, a×3 is inductively defined based on the result of a×2, and so on. Hence, all forms of multiplication were defined except for a×0, and a/0. An axiom was inserted to state that a×0=0. a/0, however, was left undefined, and remains undefined to this day.
It is possible to define a/0; in the extended complex plane, a/0= ∞. Nevertheless, mathematicians chose not to define a/0 in our standard (Peano) arithmetic to ensure the consistency of the mathematical system. A formal system is said to be consistent if it does not contain any contradictions. If division by zero is allowed, it becomes possible to use arithmetic properties to prove absurd, contradictory results like 1 = 0 (see below). Therefore, a/0 was purposely left undefined.
This proof only works because multiplying both sides by 1/(a-1) is a division by zero in disguise.
Though division by zero is undefined, it is very similar to division by a small number. For example, in the equation: 1/(6.3×10^–15)=1.6×10^14, (6.3×10^–15)m is the approximate total length of 6 protons, while (1.6×10^14)m^2 is the estimated surface area of the Pacific Ocean. As we would describe 6 protons as “non-existent”, and describe the Pacific Ocean as “endless”, this division is similar to a division by zero. This process is portrayed formally in mathematics using limits: lim(x→0+) a/x → ∞, where 0+ represents an infinitesimally small positive number. Therefore, limits are a way to perform divisions which are similar to divisions by zero.
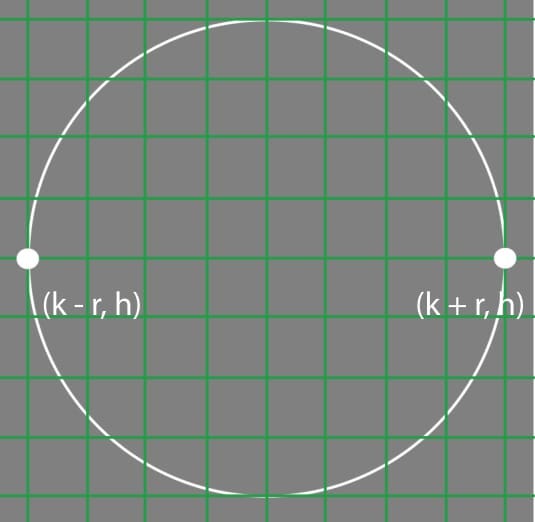
Limits where the denominator tends towards zero can provide important mathematical results. For example, say we wish to calculate the co-ordinates of the horizontal vertexes of a circle of the equation: (x-k)^2+ (y-h)^2=r^2. The gradient of the circle is given as dy/dx=-(x-k)/(y-h) . The gradient of the circle is infinite at both its horizontal vertexes, i.e. -(x-k)/(y-h)→ ∞. For the gradient to tend towards infinity, the denominator must tend towards zero, which is accomplished by having y →h. Therefore, we will substitute y=h into (x-k)^2+ (y-h)^2=r^2 to get the co-ordinates (k±r, h). Finally, there is a concept in mathematics called indeterminate forms. Common indeterminate forms include, but are not limited to 0/0, ±∞/±∞, 0^0, ∞-∞, ∞^0, ∞×0, and many of these forms can be converted interchangeably. Limits often involve indeterminate forms, for example, lim(x→1) (x^2–2x+1)/(x-1) →0/0. Mathematicians have discovered a truly remarkable rule to evaluate such limits, but this article’s scope is too small to contain it. Limits and division by infinitesimals are integral parts of mathematics, especially calculus.
The division by zero is by no means mathematically incomprehensible. In most arithmetic models, a direct division by zero is undefined to prevent contradictory results. Nevertheless, there are many instances where we will consider division by zero by using limits and infinitesimals. The division by zero is undefined, but not always meaningless.

References and Further Reading

Wang, H. (1957). The Axiomatization of Arithmetic. The Journal of Symbolic Logic, 22(2), 145–158. doi:10.2307/2964176
Eakins, B.W., & Sharman, G.F. (2009, March 27). Volumes of the World’s Oceans from ETOPO1.
Meskina, Y. (1999). Diameter Of A Proton.
 

ゼロ除算の発見は日本です：

∞？？？
∞は定まった数ではない・・・・・
人工知能はゼロ除算ができるでしょうか：

とても興味深く読みました：
ゼロ除算の発見と重要性を指摘した：日本、再生核研究所


ゼロ除算関係論文・本


God’s most important commandment

never-divide-by-zero-meme-66

Even more important than “thou shalt not eat seafood”
Published by admin, on October 18th, 2011 at 3:47 pm. Filled under: Never Divide By Zero Tags: commandment, Funny, god, zero • Comments Off on God’s most important commandment
http://thedistractionnetwork.com/.../never-divide.../page/4/

1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html

再生核研究所声明371（2017.6.27）ゼロ除算の講演―　国際会議　https://sites.google.com/site/sandrapinelas/icddea-2017　報告

ソクラテス・プラトン・アリストテレス　その他
https://ameblo.jp/syoshinoris/entry-12328488611.html

Ten billion years ago　DIVISION By ZERO：
https://www.facebook.com/notes/yoshinori-saito/ten-billion-years-ago-division-by-zero/1930645683923690/

One hundred million years ago　DIVISION By ZERO
https://www.facebook.com/.../one-hundred-million-years-ago


ゼロ除算は定義が問題です：

再生核研究所声明　１４８（2014.2.12）　100/0=0,  0/0=0　－　割り算の考えを自然に拡張すると　―　神の意志 https://blogs.yahoo.co.jp/kbdmm360/69056435.html

再生核研究所声明１７１（2014.7.30）掛け算の意味と割り算の意味　―　ゼロ除算100/0=0は自明である？http://reproducingkernel.blogspot.jp/2014/07/201473010000.html


Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.

私は数学を信じない。　アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。1423793753.460.341866474681。

Einstein's Only Mistake: Division by Zero

#divide by zero

TOP DEFINITION
  
A super-smart math teacher that teaches at HTHS and can divide by zero.
Hey look, that genius’s IQ is over 9000!
by Lawlbags! October 21, 2009


Dividing by zero is the biggest epic fail known to mankind. It is a proven fact that a succesful division by zero will constitute in the implosion of the universe.
You are dividing by zero there, Johnny. Captain Kirk is not impressed.

Divide by zero?!?!! OMG!!! Epic failzorz

3
  
Divide by zero is undefined.
Divide by zero is undefined.
by JaWo October 28, 2006

1) The number one ingredient for a catastrophic event in which the universe enfolds and collapses on itself and life as we know it ceases to exist.

2) A mathematical equation such as a/0 whereas a is some number and 0 is the divisor. Look it up on Wikipedia or something. Pretty confusing shit.

3) A reason for an error in programming
Hey, I divided by zero! ...Oh shi-

a/0

Run-time error: '11': Division by zero
by DefectiveProduct September 08, 2006

When even math shows you that not everything can be figured out with math. When you divide by zero, math kicks you in the shins and says "yeah, there's kind of an answer, but it ain't just some number."

It's when mathematicians become philosophers.
Math:
Let's say you have ZERO apples, and THREE people. How many apples does each person get? ZERO, cause there were no apples to begin with

Not-math because of dividing by zero:
Let's say there are THREE apples, and ZERO people. How many apples does each person get? Friggin... How the Fruitcock should I know! How can you figure out how many apples each person gets if there's no people to get them?!? You'd think it'd be infinity, but not really. It could almost be any number, cause you could be like "each person gets 400 apples" which would be true, because all the people did get 400 apples, because there were no people. So all the people also got 42 apples, and a million and 7 apples. But it's still wrong.
by Zacharrie February 15, 2010

投稿者 時刻:

0 件のコメント:

コメントを投稿

登録: コメントの投稿 (Atom)