寻访数学之王高斯的遗迹  精选
精选

7224 高斯一韦伯纪念碑

7348高斯像
作者 高关中(德国汉堡)2017/10/15
记得小时候,阅读《十万个为什么》这类科普读物,对一个数学故事记忆特深,至今难忘。故事说的是:一天,老师给学生们布置一道课堂作业:“1加2、加3、加4,一直加到100,总数是多少?”学生们开始一个数、一个数去加。一两分钟后,正当大家还在紧张地计算时,有个学生已经报出答案是5050。老师惊奇地问他,为什么算得这样快。这位学生从容不迫地回答:“1+100是101,2+99是101,3+98也是101,一共有50对这样的数,所以总数是101乘以50,就是5050。”“算得太妙了!”老师受到了震动,自言自语地说,“可是我从来没有教过他们呀。”这个数学小神童就是高斯(Karl-friedrich Gauß),他运用的正是算术级数的求和公式。
后来在大学的数学课里,我又学到了高斯分布(概率论中的钟形曲线,正态分布为其典型)、高斯函数、高斯积分等等,这些都是以高斯命名的数学内容。虽然我后来改行计算机软件和企管,并未从事数学专业,但对这位世界级大师一直敬佩有加,何况他也姓高(开个玩笑)。
德国中北部的格廷根(Göttingen)是著名的大学城。在德国,格廷根和海德堡相当于英国的剑桥和牛津,早就知道高斯曾长期在格廷根任教,所以这次一到格廷根,我就到处寻找与高斯有关的遗迹。还真让我找到几处。市南城墙外草地上竖立着高斯一韦伯(Wilhelm Eduard Weber,1804-1891)纪念碑。这两位科学家一坐一站,似乎正在讨论那千古不朽的电磁现象。他们共同开创了电磁理论,1833年发明电磁电报。老城内河渠旁的米歇埃利楼(Michaelishaus)是他们做物理实验的地方,后来物理学家普朗特(LudwigPrandtl,1875-1953)在此研究飞机升空的理论,被誉为“空气动力学之父”,他最出色的弟子叫冯·卡门(Theodore von Kármán,1881-1963),任教加州理工,是我国导弹之父钱学森(1911-2009)的导师。哎,扯远了,回过头继续说。市东南郊的天文台(Sternwarte)是高斯工作过的地方。他担任教授和天文台长期间,格廷根曾是数学世界的“麦加”圣地。格廷根大学以高斯而骄傲。城北距新校区不远的格大老教学楼(Auditorium Maximum)的正立面,塑有四位建校恩公的塑像和九位最著名教授的头像,高斯赫然位列其中,头像就在右翼上侧的中央。格廷根还有高斯路(Gaußstraße,新市政厅南侧),高斯公园(Gauß-Garten),甚至以高斯命名的酒馆。在西南郊10公里的德兰斯费尔德(Dransfeld)建有高斯博物馆(Gauß-Museum)。
其实高斯并不是在格廷根出生的。他的家乡是格廷根东北100多公里的不伦瑞克(Braunschweig)。高斯出生于1777年4月30日,家世普通,父亲为园丁兼泥水匠,有时忙不过来,会雇些帮工。幼年时高斯就显示出了数学方面的非凡才华,曾纠正其父计算工资的错误。少年高斯的聪颖早慧使他得到不伦瑞克公爵的垂青。公爵资助他读完卡特林文法高中(Gymnasium Catharineum),进入卡洛林学院(CollegiumCarolinum)学习,1795年继而又送他入格廷根大学深造。
在格廷根大学的第一年,19岁的高斯就用代数方法解决了两千多年来对正几边形用直尺和圆规几何作图的世界性难题。他用尺规做出了正17边形,这是他一生的骄傲。他还同时给出了单用直尺和圆规根本不可能做出正7边形、正9边形、正11边形、正13边形和正14边形的证明。1799年高斯把证明代数基本定理(关于多项式根的定理)的论文寄给黑尔姆施泰特大学(Helmstedt,在不伦瑞克以东40公里)的数学教授,未到校求学,就直接获得了博士学位。1801年他发表了第一部科学论著《算术研究》(Disquisitiones arithmeticae),立即在国际数学界声名鹊起。《算术研究》是数学史上为数不多的经典著作之一,它开辟了数论研究的全新时代。
聪明勤奋加上好运(洪堡等人的推荐),高斯30岁就成为格廷根大学数学教授,并兼任刚建成的格廷根天文台台长。此前,他已被选为英国皇家学会会员。他还是法国科学院和其他许多科学院的院士。在天文台的工作激发了他在应用数学和天文学方面的兴趣,这也是发挥数学才能的良好平台。高斯在格大一直工作到去世。
48年的平稳生活,使高斯无衣食之忧,充分地发挥了自己的数学才能,对数学做出了辉煌的贡献。他的工作影响了数学和数学物理的几乎每一个领域。
高斯对超几何级数、数论、代数学、复变函数、概率统计、椭圆函数论都有重大的贡献。他的曲面论是近代微分几何的开端。其曲面理论后来被他的学生黎曼(Bernhard Riemann,1826-1866,也在格廷根学习并任教)所发展,成为爱因斯坦广义相对论的数学基础。高斯建立了最小二乘法,并发表了3部相关的著作。他于1818年就提出了非欧几里得几何可能性的思想,虽然生前未发表,但实际上他是非欧几何的创始人之一。此外,他对向量分析,关于正态分布的正规曲线、质数定理的演算等的研究也取得了成果。
在天文学方面,高斯创立了一种可以计算行星椭圆轨道的方法,能准确地预测出行星的位置。对物理学和大地测量学也有深刻的研究。
高斯搞研究立论极端谨慎,“少些,但是要成熟”,是他的原则。这使得他生前发表的作品,比起他一生中所做的大量研究来说相对地要少得多。他去世后,弟子们整理出版的高斯全集竟有12卷之多。
高斯的工作改变了整个数学的面貌。世人公认他和阿基米德(他算出球体体积是圆柱的三分之二)和牛顿(发明微积分)并列,是人类历史上三个最伟大的数学家之一,有人赞誉他为数学之王。德国10马克纸币上就印着他的头像,背面是高斯工作用的仪器。当年几乎天天用这样的票子,可惜2002年德国改用欧元后,这一马克纸币就退出了流通。
高斯1855年2月23日在格廷根逝世,他的墓就在老城东南城墙外,墓地位于一个公园中,附近有小池塘,距多功能的格廷根市厅(Stadthalle)不远。墓碑耸立于绿蔓之上,适度装饰雕刻中镶嵌着高斯的侧面铜像。数学奇才高斯就安息在这里,与他工作终身的小城永远在一起。他的名言“数学,科学的皇后”永远为人们所牢记。
15张照片见
とても興味深く読みました:
再生核研究所声明367(2017.5.18)数学の真実を求める方、数学の研究と教育に責任を感じる方へ
(「明日ありと 思う心の仇桜 夜半に嵐の 吹かぬものかは」 ― 親鸞聖人)
そもそも数学とは何だろうかと問うことは大事である。しかしながら、生きる意味を問うことは より根源的で大事な問いである。数学についても人生についても述べてきた:(No.81、2012年5月(PDFファイル432キロバイト) -数学のための国際的な社会...www.jams.or.jp/kaiho/kaiho-81.pdf)。
数学とは、公理系、仮定系を設定すると、このようなことが言えるというものである。公理系の上に、いろいろな概念や定義を導入して数学は発展するがその全貌や本質を捉えることは何時まで経っても人間の能力を超えた存在で不可能であろう。しかしながら、人それぞれの好みを越えて、完成された理論は人間を越えて存在する客観性を有すると信じられている。万有引力の法則など物理法則より数学の理論は不変で確かな存在であろう。
数学が関係の編みのようなものであると見れば、数学の発展の先や全貌は 人間を越えて本質的には存在すると言える。例えばニュートンの万有引力の発見は、物理学の発展から必然的と言えるが、数学の発展の先はそれよりも必然的であると考えられる。その意味では、数学では特に要求されない限り、じっくりと落ち着いて楽しむように研究を進められるであろう。
ところで、ゼロで割る問題、ゼロ除算であるが、これは誠に奇妙な歴史的な事件であると言える。
ゼロで割れないは 小学校以来の世界の常識であり、アリストテレス以来の考えであると言う。オイラーやアインシュタインなども直接関わり、数学的には確定していたが、不可能性に対する興味とともに、計算機科学と相対性の理論の関係で今でも議論が続けられている。
ところが、誠に奇妙な事実が存在する。ゼロの発見者、マイナスの数も考え、算術の四則演算を確立されたBrahmagupta (598 -668 ?) は 既に、そこで628年、0/0=0 と定義していたという。しかしながら、それは間違いであると 今でも判断されていて今日に至っている。今でもゼロ除算について諸説が有って、世界やグーグルの世界でも混乱している。何十年も研究を続けて、本を出版したり、論文を公表している者が4,5人、あるいはグループで研究している者もいるが、それらは間違いである、不適当であると説得を続けている。ゼロ除算について無駄な議論や情報が世界に氾濫していると言える。
再生核研究所では、ゼロ除算発見3周年を経過し、広く議論してきたので、ゼロ除算の発見を宣言している(Announcement 362: Discovery of the division by zero as $0/0=1/0=z/0=0$ (2017.5.5)})。詳しい解説も3年間続け
(数学基礎学力研究会のホームページ
URLは
)、論文も発表、学会、国際会議などでも報告してきている。
何と創始者の結果は実は正しく、適当であることが沢山の数学の具体的な例と発展から、明らかにされてきた。ところがゼロ除算は、アリストテレスの連続性の概念を変え、2000年以上の伝統を有するユークリッド空間に全く新しい面が加わり、現代数学の初歩全般に大きな影響を与えることが分かってきた。
我々の空間の認識は間違っており、我々が学んでいる数学は、基本的なところで、欠落していて、真実とはかなり程遠く、実は数学はより完全でもっと美しいことが分かってきた。我々は年々不完全で不適当な数学を教えていると言える。
このような多くの大きな変化にはとても個人では対応できず、対応には大きな力が必要であるから、数学の愛好者や、研究者、教育者などの積極的な協力、教育、研究活動への参画、理解、援助などをお願い致したい。ゼロ除算の歴史は 人類の恥になるだろう。人々はゼロ除算の発展から、人間とはどのようなものかを沢山 学べるのではないだろうか。
以 上
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1
-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
Relations of 0 and infinity
Hiroshi Okumura, Saburou Saitoh and Tsutomu Matsuura:
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…
http://www.e-jikei.org/…/Camera%20ready%20manuscript_JTSS_A…
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
再生核研究所声明 383 (2017.9.18): 人間の精神の高まりについての視点
題名の正確な意味の表現は難しい。そこで、具体的な例を挙げて意図していることをより明らかにしよう。
小学生時代を回想しよう。 低学年ではどんどん世界が広がっていくようで、知識も情報も世界も段々、どんどん広がりどんどん世界が見えるようになっていくと感じられるだろう。 それと同時に 過去の自分の様、様子が良く見える、分かる様に感じられるだろう。 このような現象は、登山でどんどん登って行くと視野が開けて、辿ってきた様、情景がすっかり見え全体の様子が分かるような経験にもみられる。このような事は旅行で ある小さな町を訪れ、滞在しているにつれて 町全体の様子が段々分かってきて、町全体をあるイメージで捉えられるようになるだろう。最初の段階で戸惑っていた自分を知ることが出来るだろう。これらの現象は様様の研究や学問、芸術、修業等についてもみられるといえる。― ある意味での進化である。 ここでは、そのような現象を、登山の例から 人間精神の高まりと表現した。正確な表現は心の問題であるから難しい。大きな特徴は段々今までの状況を含むような形で、知識や情報が拡大して、心も質的に変化して以前の状況をより広い視点から捉えられるように成長、進んでいることである。
人生とは何か、人間とは何かの基本的な 方向として、この意味における人間の精神の高まりがあると考えられる。逆に考えてみれば、知識や情報が拡大し、精神の高まりがなければ、必ず、停滞、退屈になり、そのような生活には飽きて、生き生きした人生にはならないのではないだろうか。人間、生物的な 本能的な欲求がある程度満たされれば、必ず、情報や知識を欲求し、やがて神の意思を知りたいという真智への愛に至るのではないだろうか。 この過程にみられる、人間の精神の高まり の様子、 状況に関心を持つ。
人間は真理を追究し、情報、知識の増大方向で進むが どんどん山頂を目指して進む時、 我々の精神全体はどのように変化していくであろうか、人間とはどのように成長していくであろうか。 数学界の天才、ニュートンとライプニッツは 生涯微積分学の発見の先駆者たるを主張して、裁判闘争を続けていたという、お粗末とも言える、事実が存在する。他方、精神の高まりを象徴する用語として、人物たる人物、人格者、覚者、賢人、悟りの境地、聖人などの理想を表す概念が存在する。― 人類自身、全体があたかも子供たちである様に見えてしまう進化した人間を想定すると慄然とするだろう。人生、世界、人類さえみえてしまう者の存在、思い当たる人として お釈迦様などが考えられよう。
ゼロ除算の発見で、人生とはゼロから始まり、何かが拡大を続け、やがて突然にゼロに帰すると表現した。この拡大は 正確には何を意味するであろうか。知識や情報、経験の増大は基本的であるが、覚性度なども気になる要素ではないだろうか。どんどん気づき、世界がどんどん見えてくる面である。
人生、精神的な高まりを通して成人を迎え、円熟期を迎えるが、人間の成長の理想的な境地とは何であろうか。知識を沢山集めてものしりになったり、どんどん発見や発明を続けていけば良いのだろうか。沢山良いものを発見したり、発明していけば良いのだろうか。
人間とは どのように作られているのかと 問う。― 人間存在の意義を求めている。
ある山頂に達して、人生、世界とは そのようなものであるとの見識に達した時、その心情のいろいろな在り様と いろいろな差は どのように解釈されるべきであろうか?
良き、人間とは、人生とはどのようなものであろうか?
― しかしながら、人生における基本定理、 人生の意義は感動することにある はそのような思考の基本になるのではないだろうか。
以 上
再生核研究所声明 382 (2017.9.11): ニュートンを越える天才たちに-育成する立場の人に
次のような文書を残した: いま思いついたこと:ニュートンは偉く、ガウス、オイラーなども 遥かに及ばないと 何かに書いてあると言うのです。それで、考え、思いついた。 ガウス、オイラーの業績は とても想像も出来なく、如何に基本的で、深く、いろいろな結果がどうして得られたのか、思いもよらない。まさに天才である。数学界にはそのような天才が、結構多いと言える。しかるに、ニュートンの業績は 万有引力の法則、運動の法則、微積分学さえ、理解は常人でも出来き、多くの数学上の結果もそうである。しかるにその偉大さは 比べることも出来ない程であると表現されると言う。それは、どうしてであろうか。確かに世界への甚大な影響として 納得できる面がある。- 初めて スタンフォード大学を訪れた時、確かにニュートンの肖像画が 別格高く掲げられていたことが、鮮明に想い出されてくる。- 今でもそうであろうか?(2017.9.8.10:42)。
万物の運動を支配する法則、力、エネルギーの原理、長さ、面積、体積を捉え、傾き、勾配等の概念を捉えたのであるから、森羅万象のある基礎部分をとらえたものとして、世界史における影響が甚大であると考えれば その業績の大きさに驚かされる。
世界史における甚大な影響として、科学上ではないが、それらを越える、宗教家の大きな存在に まず、注意を喚起して置きたい。数学者、天文学者では ゼロを数として明確に導入し、負の数も考え、算術の法則(四則演算)を確立し、ゼロ除算0/0=0を宣言したBrahmagupta (598 -668 ?) の 偉大な影響 にも特に注意したい。
そのように偉大なるニュートンを発想すれば、それを越える偉大なる歴史上の存在の可能性を考えたくなるのは人情であろう。そこで、天才たちやそれを育成したいと考える人たちに 如何に考えるべきかを述べて置きたい。
万人にとって近い存在で、甚大な貢献をするであろう、科学的な分野への志向である。鍵は 生命と情報ではないだろうか。偉大なる発見、貢献であるから具体的に言及できるはずがない。しかしながら、科学が未だ十分に達しておらず、しかも万人に甚大な影響を与える科学の未知の分野として、生命と情報分野における飛躍的な発見は ニュートンを越える発見に繋がるのではないだろうか。
生物とは何者か、どのように作られ、どのように活動しているか、本能と環境への対応の原理を支配する科学的な体系、説明である。生命の誕生と終末の後、人間精神の在り様と物理的な世界の関係、殆ど未知の雄大な分野である。
情報とは何か、情報と人間の関係、影響、発展する人工知能の方向性とそれらを統一する原理と理論。情報と物の関係。情報が物を動かしている実例が存在する。
それらの分野における画期的な成果は ニュートンを越える世界史上の発見として出現するのではないだろうか。
これらの難解な課題においてニュ-トンの場合の様に常人でも理解できるような簡明な法則が発見されるのではないだろうか。
人類未だ猿や動物にも劣る存在であるとして、世界史を恥ずかしい歴史として、未来人は考え、評価するだろう。世の天才たちの志向について、またそのような偉大なる人材を育成する立場の方々の注意を喚起させたい。偉大なる楽しい夢である。
それにはまずは、世界史を視野に、人間とは何者かと問い、神の意思を捉えようとする真智への愛を大事に育てて行こうではないか。
以 上
































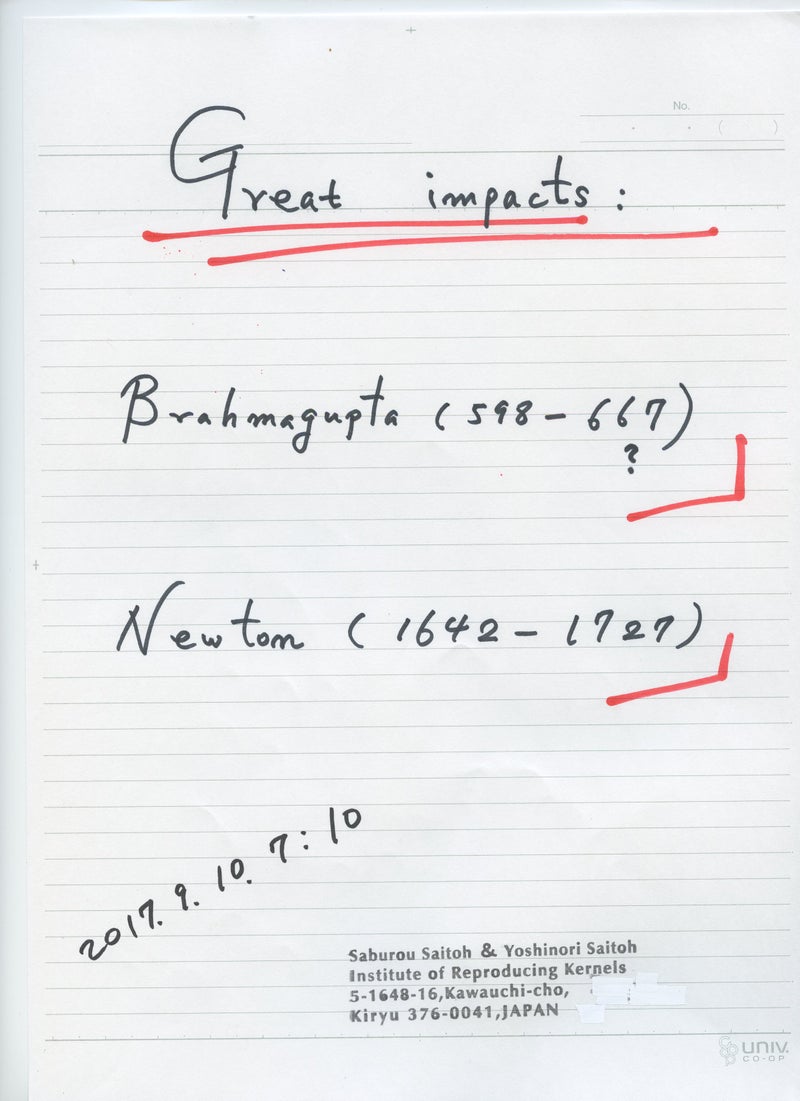





























0 件のコメント:
コメントを投稿