円周率πが現われる世界-ビュフォンの針の問題-
はじめに
円周率のπ(パイ)については、直径1の円の円周の長さを表す数値として、学生時代に学んでおり、一般の人にも馴染みのある定数である。これまでの研究員の眼の中でも、何度かπについて触れてきた。多くの人が、πは無理数とよばれるもので、その具体的な数値については小数点以下が無限に続くものであるが、ほぼ3.14であると認識しているものと思われる。
それでも、πに対しては、何となく難しい数値で、とっつきにくいものだと思っている人も多いかもしれない。ただし、πという数字は、数学の世界の幅広い場面で現われてくる。今後、πに絡む話題をいくつか紹介していきたいと思う。
今回は、有名な「ビュフォンの針の問題」についてである。
それでも、πに対しては、何となく難しい数値で、とっつきにくいものだと思っている人も多いかもしれない。ただし、πという数字は、数学の世界の幅広い場面で現われてくる。今後、πに絡む話題をいくつか紹介していきたいと思う。
今回は、有名な「ビュフォンの針の問題」についてである。
ビュフォンの針の問題
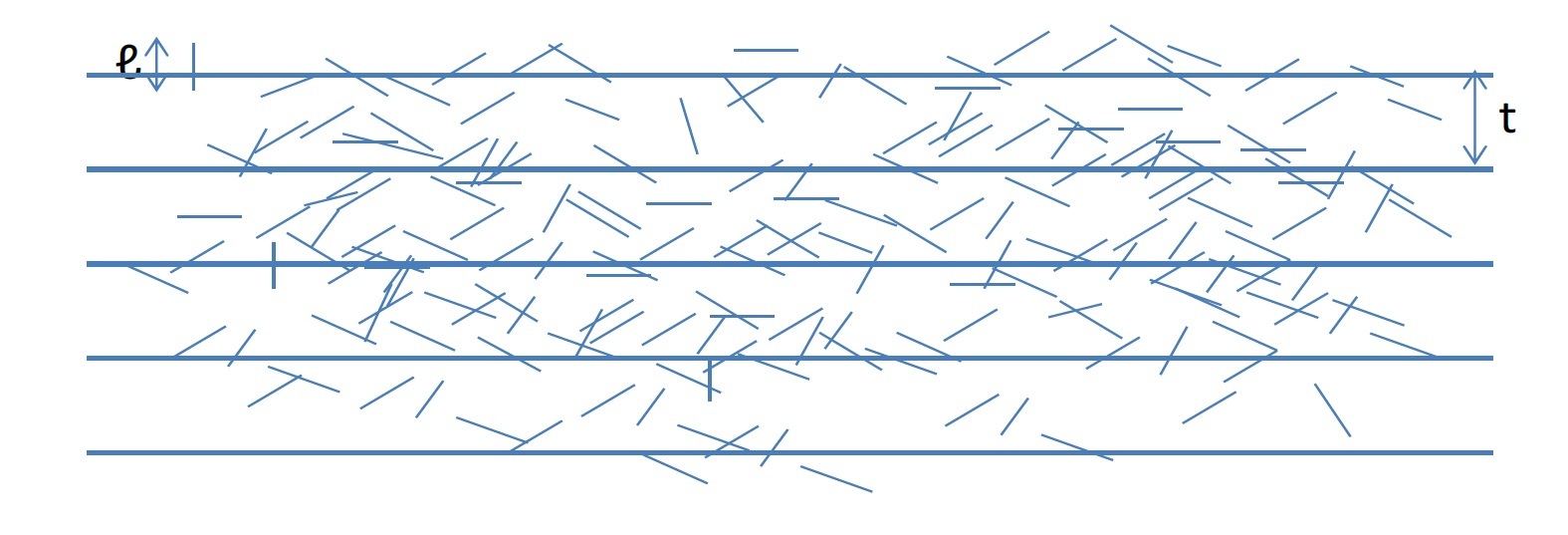
ビュフォンの針の問題とは、「間隔tで平行線が引かれた平面に、長さℓの針を無作為に投げた特に、針が平行線と交わる確率を求める。」問題である。答えは、2ℓ/tπ(ℓ≦tの場合)となる。
なお、より馴染みがあるのは、t=2ℓ とした特殊なケースで、この場合の確率は 1/π(=0.3183…)ということになる。
いずれにしても、ここで、円周率πが登場してくる。何とも不思議な感じがするのではないか。
なお、より馴染みがあるのは、t=2ℓ とした特殊なケースで、この場合の確率は 1/π(=0.3183…)ということになる。
いずれにしても、ここで、円周率πが登場してくる。何とも不思議な感じがするのではないか。
ビュフォンの針の問題の証明
これを証明するために、まずは無作為に投げられた針の位置を示すために、以下の図を考える。
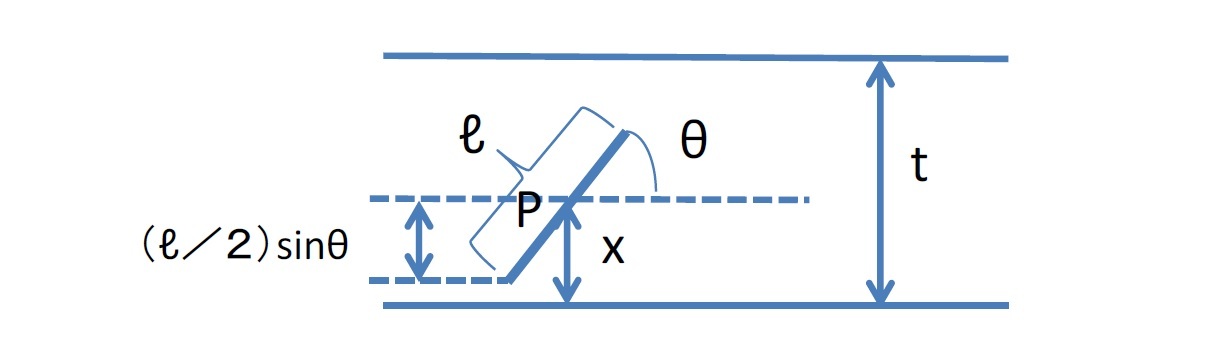
針の位置は、針の中心Pから最も近い平行線までの距離をxとし、針とこの平行性がなす角度をθとすれば、xとθで表すことができることになる。ここで、問題の確率を求めるには、容易に分かるように、0≦x≦t/2、0≦θ≦π/2(=90°)の範囲で考えれば十分である。
針の位置は、針の中心Pから最も近い平行線までの距離をxとし、針とこの平行性がなす角度をθとすれば、xとθで表すことができることになる。ここで、問題の確率を求めるには、容易に分かるように、0≦x≦t/2、0≦θ≦π/2(=90°)の範囲で考えれば十分である。
針が線と交わるのは、x≦(ℓ/2)sinθ の時となる。
ここで、「xとθがそれぞれの区間で一様分布に従う」とすれば、xとθが無作為に決まるとして、x≦(ℓ/2)sinθ となる確率は、xが0とt/2の間にある確率密度関数とθが0とπ/2の間にある確率密度関数及び2つの確率変数xとθが独立であるということから、以下の通りとなる。
ここで、「xとθがそれぞれの区間で一様分布に従う」とすれば、xとθが無作為に決まるとして、x≦(ℓ/2)sinθ となる確率は、xが0とt/2の間にある確率密度関数とθが0とπ/2の間にある確率密度関数及び2つの確率変数xとθが独立であるということから、以下の通りとなる。
この証明をみていただければわかるように、πが現われてくるのは、針がいろいろな場所に無作為に落ちる状態を表すのに、針の中心点と平行線との距離xに加えて、針と平行線が交わる角度θが用いられ、このθの一様分布を前提に確率を求めていくことになるからである。
言われてしまえば、何だそうかと思われるかもしれないし、それでも今一つしっくりこない方もおられるかもしれない。
言われてしまえば、何だそうかと思われるかもしれないし、それでも今一つしっくりこない方もおられるかもしれない。
補足
ここまでは、あくまでもℓ≦tの場合(即ち、平行線の間隔よりも針の長さが短い場合)について考えてきた。ℓ>tの場合(即ち、針の長さが平行線の間隔よりも長い場合)には、ℓsinθ>t となることもあるので、問題は簡単ではなくなる。
結論だけを示せば、以下の通りとなる。
結論だけを示せば、以下の通りとなる。
針の長さと平行線の間隔の関係という、ちょっとした前提がかわるだけで、結論は極めて複雑なものになってくる。こうしたことは世の中に往々にしてみられるものである。
ビュフォンについて
ビュフォンの針の問題を提案したビュフォン伯爵(Georges-Louis Leclerc, Comte de Buffon)(1707~1788)は、フランスの博物学者、数学者、植物学者である。数学者としてよりも、むしろ博物学者として有名である。ビュフォン伯爵は、天変地異説を否定し、自然は動植物の種を含めて徐々に変化を遂げると考えて、後の進化論の形成に影響を与えている。
さらに、数学の分野では、確率論に微分・積分の概念を導入した。なお、ビュフォンの針の問題は、逆に多くのシミュレーションを行うことで、πの近似値を求めることができることになるため、モンテカルロ法1のルーツとなったとして知られている。
さらに、数学の分野では、確率論に微分・積分の概念を導入した。なお、ビュフォンの針の問題は、逆に多くのシミュレーションを行うことで、πの近似値を求めることができることになるため、モンテカルロ法1のルーツとなったとして知られている。
1 モンテカルロ法 (Monte Carlo method) とは、シミュレーションや数値計算を乱数を発生させて行う手法。カジノで有名なモナコ公国の4つある地区の1つの名前に基づいている。
最後に
針を落として、その位置を観測するという単純な行動が、πという数学の世界の重要な数字や、モンテカルロ法という統計の世界で欠かせない手法と深く関わっているというのは、何とも面白い話ではないだろうか。
ビュフォンの針の問題は、針を平行線(等間隔の直線)が引かれた平面に落として、それが平行線に交わる確率を求める問題であるが、これを拡張して、例えば、同心円(半径が等間隔の円)が書かれた平面に落とした場合に、それが同心円に交わる確率はどうなるのか、さらには、等間隔の正方形が書かれた平面に落とした場合に、それが正方形と交わる確率はどうなるのか、といった問題を考えることもできる。
今やコンピューターを使えば、多数の試行を繰り返すことで、結果数値の概要を知ることは比較的容易にできるようになっていると思われるが、その結果を合理的に説明あるいは証明することは必ずしも容易ではない。このことは、過去の実験等に基づく観測値や経験則の説明のための理論構築に、多くの優秀な研究者等の多大な時間と労力が費やされていること、それでも未だ解決されていない問題が数多く存在している、ことが示している。
いずれにしても、単なるお遊びのように見えることでも、実は重要な法則等が含まれており、大きな発見につながっていくものである、ということを直に感じられるとしたら、それはそれで楽しいものではないかと思われるがいかがだろうか。http://www.nli-research.co.jp/report/detail/id=56991?site=nli
ビュフォンの針の問題は、針を平行線(等間隔の直線)が引かれた平面に落として、それが平行線に交わる確率を求める問題であるが、これを拡張して、例えば、同心円(半径が等間隔の円)が書かれた平面に落とした場合に、それが同心円に交わる確率はどうなるのか、さらには、等間隔の正方形が書かれた平面に落とした場合に、それが正方形と交わる確率はどうなるのか、といった問題を考えることもできる。
今やコンピューターを使えば、多数の試行を繰り返すことで、結果数値の概要を知ることは比較的容易にできるようになっていると思われるが、その結果を合理的に説明あるいは証明することは必ずしも容易ではない。このことは、過去の実験等に基づく観測値や経験則の説明のための理論構築に、多くの優秀な研究者等の多大な時間と労力が費やされていること、それでも未だ解決されていない問題が数多く存在している、ことが示している。
いずれにしても、単なるお遊びのように見えることでも、実は重要な法則等が含まれており、大きな発見につながっていくものである、ということを直に感じられるとしたら、それはそれで楽しいものではないかと思われるがいかがだろうか。http://www.nli-research.co.jp/report/detail/id=56991?site=nli
とても興味深く読みました:
再生核研究所声明314(2016.08.08) 世界観を大きく変えた、ニュートンとダーウィンについて
今朝2016年8月6日,散歩中 目が眩むような大きな構想が閃いたのであるが、流石に直接表現とはいかず、先ずは世界史上の大きな事件を回想して、準備したい。紀元前の大きな事件についても触れたいが当分 保留したい。
そもそも、ニュートン、ダーウィンの時代とは 中世の名残を多く残し、宗教の存在は世界観そのものの基礎に有ったと言える。それで、アリストテレスの世界観や聖書に反して 天動説に対して地動説を唱えるには それこそ命を掛けなければ主張できないような時代背景が 存在していた。
そのような時に世の運動、地上も、天空も、万有を支配する法則が存在するとの考えは それこそ、世界観の大きな変更であり、人類に与えた影響は計り知れない。進化論 人類も動物や生物の進化によるものであるとの考えは、 人間そのものの考え方、捉え方の基本的な変更であり、運動法則とともに科学的な思考、捉え方が世界観を根本的に変えてきたと考えられる。勿論、自然科学などの基礎として果たしている役割の大きさを考えると、驚嘆すべきことである。
人生とは何か、人間とは何か、― 世の中には秩序と法則があり、人間は作られた存在で
その上に 存在している。如何に行くべきか、在るべきかの基本は その法則と作られた存在の元、原理を探し、それに従わざるを得ないとなるだろう。しかしながら、狭く捉えて 唯物史観などの思想も生んだが、それらは、心の問題、生命の神秘的な面を過小評価しておかしな世相も一時は蔓延ったが、自然消滅に向かっているように見える。
自然科学も生物学も目も眩むほどに発展してきている。しかしながら、人類未だ成長していないように感じられるのは、止むことのない抗争、紛争、戦争、医学などの驚異的な発展にも関わらず、人間存在についての掘り下げた発展と進化はどれほどかと考えさせられ、昔の人の方が余程人間らしい人間だったと思われることは 多いのではないだろうか。
上記二人の巨人の役割を、自然科学の基礎に大きな影響を与えた人と捉えれば、我々は一段と深く、巨人の拓いた世界を深めるべきではないだろうか。社会科学や人文社会、人生観や世界観にさらに深い影響を与えると、与えられると考える。
ニュートンの作用、反作用の運動法則などは、人間社会でも、人間の精神、心の世界でも成り立つ原理であり、公正の原則の基礎(再生核研究所声明 1 (2007/1/27): 美しい社会はどうしたら、できるか、美しい社会とは)にもなる。 自国の安全を願って軍備を強化すれば相手国がより、軍備を強化するのは道理、法則のようなものである。慣性の法則、急には何事でも変えられない、移行処置や時間的な猶予が必要なのも法則のようなものである。力の法則 変化には情熱、エネルギー,力が必要であり、変化は人間の本質的な要求である。それらはみな、社会や心の世界でも成り立つ原理であり、掘り下げて学ぶべきことが多い。ダーウィンの進化論については、人間はどのように作られ、どのような進化を目指しているのかと追求すべきであり、人間とは何者かと絶えず問うて行くべきである。根本を見失い、個別の結果の追求に明け暮れているのが、現在における科学の現状と言えるのではないだろうか。単に盲目的に夢中で進んでいる蟻の大群のような生態である。広い視点で見れば、経済の成長、成長と叫んでいるが、地球規模で生態系を環境の面から見れば、癌細胞の増殖のような様ではないだろうか。人間の心の喪失、哲学的精神の欠落している時代であると言える。
以 上
再生核研究所声明315(2016.08.08) 世界観を大きく変えた、ユークリッドと幾何学
今朝2016年8月6日,散歩中 目が眩むような大きな構想が閃いたのであるが、流石に直接表現とはいかず、先ずは世界史上の大きな事件を回想して、準備したい。紀元前の大きな事件についても触れたいが当分 保留したい。
ニュートン、ダーウィンの大きな影響を纏めたので(声明314)今回はユークリッド幾何学の影響について触れたい。
ユークリッド幾何学の建設について、ユークリッド自身(アレクサンドリアのエウクレイデス(古代ギリシャ語: Εὐκλείδης, Eukleídēs、ラテン語: Euclīdēs、英語: Euclid(ユークリッド)、紀元前3世紀? - )は、古代ギリシアの数学者、天文学者とされる。数学史上最も重要な著作の1つ『原論』(ユークリッド原論)の著者であり、「幾何学の父」と称される。プトレマイオス1世治世下(紀元前323年-283年)のアレクサンドリアで活動した。)が絶対的な幾何学の建設に努力した様は、『新しい幾何学の発見―ガウス ボヤイ ロバチェフスキー』リワノワ 著松野武 訳1961 東京図書 に見事に描かれており、ここでの考えはその著書に負うところが大きい。
ユークリッドは絶対的な幾何学を建設するためには、絶対的に正しい基礎、公準、公理に基づき、厳格な論理によって如何なる隙や曖昧さを残さず、打ち立てられなければならないとして、来る日も来る日も、アレクサンドリアの海岸を散歩しながら ユークリッド幾何学を建設した(『原論』は19世紀末から20世紀初頭まで数学(特に幾何学)の教科書として使われ続けた[1][2][3]。線の定義について、「線は幅のない長さである」、「線の端は点である」など述べられている。基本的にその中で今日ユークリッド幾何学と呼ばれている体系が少数の公理系から構築されている。エウクレイデスは他に光学、透視図法、円錐曲線論、球面天文学、誤謬推理論、図形分割論、天秤などについても著述を残したとされている。)。
ユークリッド幾何学、原論は2000年以上も越えて多くの人に学ばれ、あらゆる論理的な学術書の記述の模範、範として、現在でもその精神は少しも変わっていない、人類の超古典である。― 少し、厳密に述べると、ユークリッド幾何学の基礎、いわゆる第5公準、いわゆる平行線の公理は徹底的に検討され、2000年を経て公理系の考えについての考えは改められ― 公理系とは絶対的な真理という概念ではなく、矛盾のない仮定系である ― 、非ユークリッド幾何学が出現した。論理的な厳密性も徹底的に検討がなされ、ヒルベルトによってユークリッド幾何学は再構成されることになった。非ユークリッド幾何学の出現過程についても上記の著書に詳しい。
しかしながら、ユークリッド幾何学の実態は少しも変わらず、世に絶対的なものがあるとすれば、それは数学くらいではないだろうかと人類は考えているのではないだろうか。
数学の不可思議さに想いを致したい(しかしながら、数学について、そもそも数学とは何だろうかと問い、ユニバースと数学の関係に思いを致すのは大事ではないだろうか。この本質論については幸運にも相当に力を入れて書いたものがある:
19/03/2012
ここでは、数学とは何かについて考えながら、数学と人間に絡む問題などについて、幅.広く面白く触れたい。
)。
― 数学は公理系によって定まり、そこから、論理的に導かれる関係の全体が一つの数学の様 にみえる。いま予想されている関係は、そもそも人間には無関係に確定しているようにみえる。その数学の全体はすべて人間には無関係に存在して、確定しているようにみえる。すなわち、われわれが捉えた数学は、人間の要求や好みで発見された部分で、その全貌は分か らない。抽象的な関係の世界、それはものにも、時間にも、エネルギーにも無関係で、存在 している。それではどうして、存在して、数学は美しいと感動させるのであろうか。現代物理学は宇宙全体の存在した時を述べているが、それでは数学はどうして存在しているのであろうか。宇宙と数学は何か関係が有るのだろうか。不思議で 不思議で仕方がない。数学は絶対で、不変の様にみえる。時間にも無関係であるようにみえる。数学と人間の関係は何だ ろうか。―
数学によって、神の存在を予感する者は 世に多いのではないだろうか。
以 上
再生核研究所声明339(2016.12.26)インドの偉大な文化遺産、ゼロ及び算術の発見と仏教
世界史と人類の精神の基礎に想いを致したい。ピタゴラスは 万物は数で出来ている、表されるとして、数学の重要性を述べているが、数学は科学の基礎的な言語である。ユークリッド幾何学の大きな意味にも触れている(再生核研究所声明315(2016.08.08) 世界観を大きく変えた、ユークリッドと幾何学)。しかしながら、数体系がなければ、空間も幾何学も厳密には 表現することもできないであろう。この数体系の基礎はブラーマグプタ(Brahmagupta、598年 – 668年?)インドの数学者・天文学者によって、628年に、総合的な数理天文書『ブラーマ・スプタ・シッダーンタ』(ब्राह्मस्फुटसिद्धान्त Brāhmasphuṭasiddhānta)の中で与えられ、ゼロの導入と共に四則演算が確立されていた。ゼロの導入、負の数の導入は数学の基礎中の基礎で、西欧世界がゼロの導入を永い間嫌っていた状況を見れば、これらは世界史上でも顕著な事実であると考えられる。最近ゼロ除算は、拡張された割り算、分数の意味で可能で、ゼロで割ればゼロであることが、その大きな影響とともに明らかにされてきた。しかしながら、 ブラーマグプタはその中で 0 ÷ 0 = 0 と定義していたが、奇妙にも1300年を越えて、現在に至っても 永く間違いであるとしてされている。現在でも0 ÷ 0について、幾つかの説が存在していて、現代数学でもそれは、定説として 不定であるとしている。最近の研究の成果で、ブラーマグプタの考えは 実は正しかった ということになる。 しかしながら、一般の ゼロ除算については触れられておらず、永い間の懸案の問題として、世界を賑わしてきた。現在でも議論されている。ゼロ除算の永い歴史と問題は、次のアインシュタインの言葉に象徴される:
Blackholes are where God divided by zero. I don't believe in mathematics. George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist re-
marked that "it is well known to students of high school algebra" that division by zero is not valid; and Einstein admitted it as the biggest blunder of his life [1] 1. Gamow, G., My World Line (Viking, New York). p 44, 1970.
· 愛別離苦(あいべつりく) - 愛する者と別離すること
· 怨憎会苦(おんぞうえく) - 怨み憎んでいる者に会うこと
· 求不得苦(ぐふとくく) - 求める物が得られないこと
の四つの苦に対する人間の在り様の根本を問うた仏教の教えは人類普遍の教えであり、命あるものの共生、共感、共鳴の精神を諭されたと理解される。人生の意義と生きることの基本を真摯に追求された教えと考えられる。アラブや西欧の神の概念に直接基づく宗教とは違った求道者、修行者の昇華された世界を見ることができ、お釈迦様は人類普遍の教えを諭されていると考える。
これら2点は、インドの誠に偉大なる、世界史、人類における文化遺産である。我々はそれらの偉大な文化を尊崇し、数理科学にも世界の問題にも大いに活かして行くべきであると考える。 数理科学においては、十分に発展し、生かされているので、仏教の教えの方は、今後世界的に広められるべきであると考える。仏教はアラブや欧米で考えられるような意味での宗教ではなく、 哲学的、学術的、修行的であり、上記宗教とは対立するものではなく、広く活かせる教えであると考える。世界の世相が悪くなっている折り、仏教は世界を救い、世界に活かせる基本的な精神を有していると考える。
ちなみに、ゼロは 空や無の概念と通じ、仏教の思想とも深く関わっていることに言及して置きたい。 いみじくも高度に発展した物理学はそのようなレベルに達していると報じられている。この観点で、歴史的に永い間、ゼロ自身の西欧社会への導入が異常に遅れていた事実と経過は 大いに気になるところである。
以 上
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
Announcement 326: The division by zero z/0=0/0=0 - its impact to human beings through education and research
再生核研究所声明353(2017.2.2) ゼロ除算 記念日
2014.2.2 に 一般の方から100/0 の意味を問われていた頃、偶然に執筆中の論文原稿にそれがゼロとなっているのを発見した。直ぐに結果に驚いて友人にメールしたり、同僚に話した。それ以来、ちょうど3年、相当詳しい記録と経過が記録されている。重要なものは再生核研究所声明として英文と和文で公表されている。最初のものは
再生核研究所声明 148(2014.2.12): 100/0=0, 0/0=0 - 割り算の考えを自然に拡張すると ― 神の意志
で、最新のは
Announcement 352 (2017.2.2): On the third birthday of the division by zero z/0=0
である。
アリストテレス、ブラーマグプタ、ニュートン、オイラー、アインシュタインなどが深く関与する ゼロ除算の神秘的な永い歴史上の発見であるから、その日をゼロ除算記念日として定めて、世界史を進化させる決意の日としたい。ゼロ除算は、ユークリッド幾何学の変更といわゆるリーマン球面の無限遠点の考え方の変更を求めている。― 実際、ゼロ除算の歴史は人類の闘争の歴史と共に 人類の愚かさの象徴であるとしている。
心すべき要点を纏めて置きたい。
1) ゼロの明確な発見と算術の確立者Brahmagupta (598 - 668 ?) は 既にそこで、0/0=0 と定義していたにも関わらず、言わば創業者の深い考察を理解できず、それは間違いであるとして、1300年以上も間違いを繰り返してきた。
2) 予断と偏見、慣習、習慣、思い込み、権威に盲従する人間の精神の弱さ、愚かさを自戒したい。我々は何時もそのように囚われていて、虚像を見ていると 真智を愛する心を大事にして行きたい。絶えず、それは真かと 問うていかなければならない。
3) ピタゴラス派では 無理数の発見をしていたが、なんと、無理数の存在は自分たちの世界観に合わないからという理由で、― その発見は都合が悪いので ― 、弟子を処刑にしてしまったという。真智への愛より、面子、権力争い、勢力争い、利害が大事という人間の浅ましさの典型的な例である。
4) この辺は、2000年以上も前に、既に世の聖人、賢人が諭されてきたのに いまだ人間は生物の本能レベルを越えておらず、愚かな世界史を続けている。人間が人間として生きる意義は 真智への愛にある と言える。
5) いわば創業者の偉大な精神が正確に、上手く伝えられず、ピタゴラス派のような対応をとっているのは、本末転倒で、そのようなことが世に溢れていると警戒していきたい。本来あるべきものが逆になっていて、社会をおかしくしている。
6) ゼロ除算の発見記念日に 繰り返し、人類の愚かさを反省して、明るい世界史を切り拓いて行きたい。
以 上
追記:
The division by zero is uniquely and reasonably determined as 1/0=0/0=z/0=0 in the natural extensions of fractions. We have to change our basic ideas for our space and world:
Division by Zero z/0 = 0 in Euclidean Spaces
Hiroshi Michiwaki, Hiroshi Okumura and Saburou Saitoh
International Journal of Mathematics and Computation Vol. 28(2017); Issue 1, 2017), 1-16.
http://www.scirp.org/journal/alamt http://dx.doi.org/10.4236/alamt.2016.62007
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
http://www.ijapm.org/show-63-504-1.html
http://www.diogenes.bg/ijam/contents/2014-27-2/9/9.pdf
再生核研究所声明371(2017.6.27)ゼロ除算の講演― 国際会議 https://sites.google.com/site/sandrapinelas/icddea-2017 報告
http://ameblo.jp/syoshinoris/theme-10006253398.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12276045402.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12263708422.html
1/0=0、0/0=0、z/0=0
http://ameblo.jp/syoshinoris/entry-12272721615.html
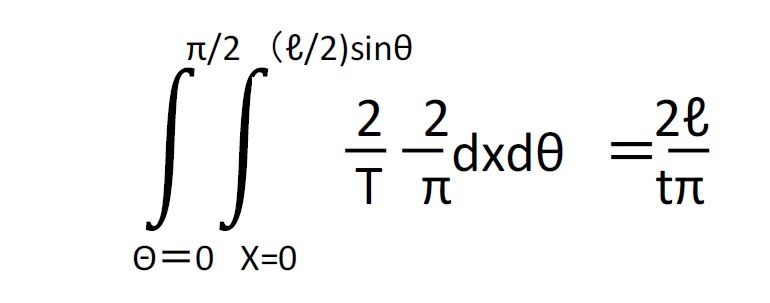
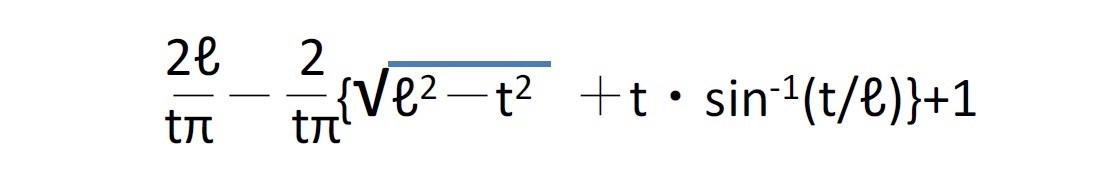






















































0 件のコメント:
コメントを投稿