京都新聞 4月24日(日)20時44分配信
縄文人の人口減は偏食原因か 食の多様性失い変化に弱く
三内丸山遺跡の近くで出土した約5300年前の土器の破片を手にする羽生教授。土器が作られた年代によって型式は異なる
日本の人口減少が課題となっているが、実は約4300年前の縄文時代にも大きく減った。日本における「最初の人口減少」とも言われ、気候変動による寒冷化が原因とする説が有力だ。しかし、総合地球環境学研究所の羽生淳子教授は「縄文人が採取する食物が偏った結果、わずかな環境の変化に対応できなくなったのが原因」という仮説を提唱している。人間は縄文時代から、炭水化物に大きく依存して食の多様性を失わせ、その弊害を被っていたというのだ。
羽生教授は青森市の三内丸山遺跡など縄文時代の遺跡を研究している。同遺跡は約5900年前から1600年続いた集落だ。最盛期には数百人が暮らしたという説もあり、縄文時代では最大級の規模だった。
「遺跡の人口を詳細に検討すると、寒冷化より前に既に人口が減っているんです」。羽生教授は指摘する。住居跡から推測すると、同遺跡の人口が減り始めるのは約4900年前と、寒冷化が始まったとされる時期よりも600年ほど早い。人口減少の理由は、気候変動だけでは説明がつかないというわけだ。
羽生教授は、出土する石器に注目した。獲物を捕まえる弓矢の矢尻に使った石ぞくや植物をすりつぶした磨石(すりいし)など、石器の出土数から当時の食生活が推測できる。食生活と人口には相関があるという。
約5600~5200年前の同遺跡からは、磨石や石ぞくなどが満遍なく出土し、人々が動物も植物もよく食べていたと推測できる。この間の住居は約30軒を超えなかった。その後、出土する石器の大半を磨石が占めるようになり、クリやトチの実など植物を多く採取したと考えられる。住居は増え始めて人口増加をうかがわせる。
しかし約60軒以上の住居のあった人口最盛期の4900年前になると、出土する石器は石ぞくが多くなり、狩猟で動物を仕留める機会が増加したとみられる。周辺の木の実の収穫が減って、炭水化物を主食にできなくなったと推測できる。その後の100年で住居跡は十数軒まで急減し、人口減の局面を迎える。羽生教授は「食の多様性が失われ、わずかな気候の変動でも食物確保をできなくなり、一度は最盛期を迎えた人口も減少してしまった」と考える。
縄文時代には、人口の大半が東日本に偏る一方、約5千年前の人口は26万人に上るという推定もある。数百人規模の同遺跡の分析をそのまま日本全体に当てはめることはできない。しかし羽生教授は「三内丸山は当時の最大級の遺跡。東日本で起こった出来事を推測する大きな鍵」と話す。その上で「食料の単一化傾向が、縄文時代の人口減少の原因だとすれば、品種の多様性が問題となる農業にも参考になる」と語り、縄文人の生活史が現代の課題に通じると強調する。http://headlines.yahoo.co.jp/hl?a=20160424-00000018-kyt-sctch
Announcement 213: An interpretation of the identity $ 0.999999...... =1$
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 213: An interpretation of the identity $ 0.999999...... =1$
}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
\date{}
\maketitle
{\bf Abstract: } In this announcement, we shall give a very simple interpretation for the identity: $ 0.999999......=1$.
\bigskip
\section{ Introduction}
On January 8, 2008, Yuusuke Maede, 8 years old boy, asked the question, at Gunma University, that (Announcement 9(2007/9/1): Education for genius boys and girls):
What does it mean by the identity:
$$
0.999999......=1?
$$
at the same time, he said: I am most interesting in the structure of large prime numbers. Then, a teacher answered for the question by the popular reason based on the convergence of the series: $0.9, 0.99, 0.999,... $. Its answer seems to be not suitable for the 8 years old boy with his parents (not mathematicians). Our answer seems to have a general interest, and after then, such our answer has not been heard from many mathematicians, indeed.
This is why writting this announcement.
\medskip
\bigskip
\section{An interpretation}
\medskip
In order to see the essence, we shall consider the simplist case:
\begin{equation}
\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + ... = 1.
\end{equation}
Imagine a tape of one meter length, we will give its half tape: that is,
\begin{equation}
\frac{1}{2}.
\end{equation}
Next, we will give its (the rest's half) half tape; that is, $\frac{1}{2}\cdot \frac{1}{2} = \frac{1}{2^2}$, then you have, altogether
\begin{equation}
\frac{1}{2} + \frac{1}{2^2} .
\end{equation}
Next, we will give the last one's half (the rest's half); that is, $\frac{1}{2}\cdot \frac{1}{2} \cdot \frac{1}{2}= \frac{1}{2^3}$,
then, you have, altogether
\begin{equation}
\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3}.
\end{equation}
By this procedure, you will be able to obtain the small tapes endressly. Imagine all the sum as in the left hand side of (2.1). However, we will see that this sum is just the division of the one meter tape. Therefore, we will be able to confim the identity (2.1), clearly.
The question proposed by Y. Maede is just the small change the ratio $\frac{1}{2}$ by $\frac{9}{10}$.
\bigskip
\section{ Conclusion}
Y. Maede asked the true sense of the limit in the series:
$$
0.999999.....
$$
that is, this series is approaching to 1; however, is it equal or not ? The above interpretation means that the infinite series equals to one and it is just the infinite division of one. By this inverse approarch, the question will make clear.
\medskip
\bigskip
\section{Remarks}
Y. Maede stated a conjecture that for any prime number $p$ $( p \geqq 7)$, for $1$ of $ - 1$
\begin{equation}
11111111111
\end{equation}
may be divided by $p$ (2011.2.6.12:00 at University of Aveiro, by skype)
\medskip
(No.81, May 2012(pdf 432kb)
www.jams.or.jp/kaiho/kaiho-81.pdf).
\medskip
This conjecture was proved by Professors L. Castro and Y. Sawano,
independently. Y. Maede gave later an interesting interpretation for his conjecture.
\medskip
(2015.2.26)
\end{document}
\title{\bf Announcement 214: Surprising mathematical feelings of a 7 years old girl
}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
\date{}
\maketitle
{\bf Abstract: } In this announcement, we shall give the two surprising mathematical feelings of 7 years old girl Eko Michiwaki who stated the division by 3 of any angle and the division by zero $100/0=0$ as clear and trivial ones. As well-known, these famous problems are historical, and her results will be quite original.
\bigskip
\section{ Introduction}
We had met, 7 years old girl, Eko Michiwaki on November 23, 2014 at Tokyo Institute of Technology and August 23, 2014 at Kusatu Seminor House, with our colleagues. She, surprisingly enough, stated there repeatedly the division by 3 of any angle and the division by zero $100/0=0$ as clear and trivial ones. As well-known, these famous problems are historical and her results will be quite original.
\section{The division of any angle by 3}
\medskip
Eko Michiwaki said:
divide a given angle with 4 equal angles; this is simly done. Next, we divide one divided angle
with 4 equal angles similarly and the three angles add to other 3 angles. By continuing this procedure, we will be able to obtain the division by 3 of any angle. Her idea may be stated mathematically as follows:
$$
\frac{1}{4} + \frac{1}{4^2} + \frac{1}{4^3} + ... ...= \frac{1}{3}.
$$
However, her idea seems to be more clear than the above mathematical formula. For this sentence, see \cite{ann3} for the sense of the limit.
\bigskip
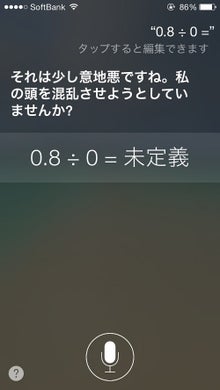
\section{The division by zero $100/0=0$}
\medskip
As we stated in \cite{ann1}, she stated that division by zero $100/0=0$ is clear and trivial for our recent results \cite{cs,kmsy,s,ttk}. The basic important viewpoint is that division and product are different concepts and the division by zero $100/0=0$ is clear and trivial from the own sense of the division, independently of product \cite{ann1}. From the viewpoint, our colleagues stated as follows:
\medskip
On July 11, 2014, Seiichi Koshiba and Masami Yamane said at
Gunma University:
The idea for the division of Hiroshi Michiwaki and Eko Michiwaki (6 years
old daughter) is that division and product are different concepts and they
were calculated independently for long old years, by repeated addition and
subtraction, respectively. Mathematicians made the serious mistake for very
long years that the division by zero is impossible by considering that division
is the inverse operation of product. The division by zero was, however, clear
and trivial, as z/0=0, from the own nature of division.
\medskip
On February 21, 2015, Seiichi Koshiba and Masami Yamane visited our Institute and we confirmed this meaning of these sentences and the basic idea on the division by zero.
\medskip
(2015.2.27)
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{cs}
L. P. Castro and S.Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances inLinear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95.http://www.scirp.org/journal/ALAMT/
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics (in press).
\bibitem{ann1}
Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics,
Institute of Reproducing Kernels, 2014.10.22.
\bibitem{ann2}
Announcement 185: The importance of the division by zero $z/0=0$, Institute of Reproducing Kernels, 2014.11.28.
\bibitem{ann3}
Announcement 213: An interpretation of the identity $ 0.999999...... =1$, Institute of Reproducing Kernels, 2015.2.26.
\end{thebibliography}
\end{document}








0 件のコメント:
コメントを投稿