万有引力
曖昧さ回避 日本の劇団については「演劇実験室◎万有引力」をご覧ください。
万有引力(ばんゆういんりょく、英語: universal gravitation)または万有引力の法則(ばんゆういんりょくのほうそく、英語: law of universal gravitation)とは、「地上において質点(物体)が地球に引き寄せられるだけではなく、この宇宙においてはどこでも全ての質点(物体)は互いに gravitation(=引き寄せる作用、引力、重力)を及ぼしあっている」とする考え方、概念、法則のことである。
目次 [非表示]
1 歴史
1.1 前史
1.1.1 アリストテレスの考え方
1.1.2 中世の考え方
1.1.3 地上の範囲での、従来の自然学への疑念と改良
1.2 ニュートン、フック、ハリーらの活動
1.2.1 ニュートンの発想 ~ガリレオ動力学の天体への適用~
1.2.2 同時期の、フックによる引力に関する活動
1.3 『自然哲学の諸原理』における、万有引力という考え方の公表
2 ニュートン力学と重力
3 ありがちな誤解
4 評価
5 万有引力の法則、その後
5.1 一般相対性理論と重力
5.2 素粒子物理学と重力
5.3 量子重力
6 出典
7 関連項目
歴史[編集]
前史[編集]
この万有引力という見方がどのようなものであるか、その正しい位置づけ・真価を理解するには、一旦、この概念が生み出される以前に人々がこの世界をどのようにとらえていたのか、その考え方、世界の見え方(世界観)に寄り添って理解し、そこからどのように変えていったのか、その相違の程度を理解する必要がある。
アリストテレスの考え方[編集]
石を手から離せば自然に地面へと落ちる。古代ギリシャの哲学者アリストテレスは、その原因は、石を構成する土元素(四元素のうちの一つ)が、本来の位置である地へ戻ろうとする性質にあると考えた[1]。土元素が多いものが重い、と考え、それが多いものほど速く落ちる、と考えた[2]。
中世の考え方[編集]
中世ヨーロッパではアリストテレスの考え方が広く知られていたので、人々はそうした見方で世界を見ていた。以下のような考え方である。
我々人間は、それぞれの家に住んでいる。人間は何かの理由で家から離れることがあっても、結局はその家に帰ろうとする。動物も同じだ。地リスは地面に巣穴を持っている。何かの理由があると、たとえば危険を感じると、穴から一時的に離れることはあるが、危険がさればやはりその巣穴に戻ろうとする。鳥もそうだ。鳥も何かの理由、例えば食べ物を探すために一時的に巣から飛び立つことがあるが、結局はその巣へ帰ってくる。命あるものは全て、それぞれの性質に応じて本来の位置というものをもっていて、一時的にそこから離れることはあっても、結局はそこへ帰ろうとするものだ[1]。
生き物がそれぞれ本来の位置というのを持っているように、物(無生物)も、それぞれの性質に応じて本来の位置を持っている。たとえば小石はその本来の位置を地に持っている。焔はその本来の位置を天上に持っている[1]。
例えば、小石を空中に投げれば、小石は本来の位置から離されることになり、小石は一旦は抵抗を示しながら上に上がるが、結局はできるだけすみやかに、その本来の位置である地に戻ってこようとする[1]。
だが、無生物でも、その本来の位置を持たないと思われる存在がある。天に見える天体である。天体は永久に同じ運動を繰り返すばかりで、その本来の位置を持っていないように見える[1]。そこで中世の人々は、地上の存在と天の存在は本質的に異なっていると考え、地上の存在はただの存在であり、それに対して天の世界に属する存在、永遠に運動を繰り返す天体は、いわば霊的な存在である、と考えた[1]。中世の人々は、天の世界は地上とは全く別の法則が働いている別世界なのだ、と考えていたのである。また、天の世界の、地上とは異なった性質を説明するために、地上は四元素でできているのに対して、天体は第五元素でできている、とも考えていた。
地上の範囲での、従来の自然学への疑念と改良[編集]
さて、アリストテレスの考え、「土元素が多いものが重い、それが多いものほど速く落ちる」については、パドヴァ大学のベネデッティ(Giambattista Benedetti、1530-1590)が異論を唱えた[2]。またオランダのステヴィン(Simon Stevin、1548-1620)は、重さが10倍異なる二つの鉛玉を9メートルほど落下させ、ほとんど同時に落ちることを確かめて、このアリストテレスの理論に異議を唱えた[2]。
自然学者ガリレオ・ガリレイ(1564-1642)も、上記の中世の考え方(の一部)に疑問を投げかけた[1]。(ところで、先行する14世紀の自然学者ビュリダンはインペタス理論(いきおい理論)を提唱し、その理論では、物体を投げると手からインペタスが物体の内部に移ることで飛び続け、空気や重さなどの抵抗により内部要因のインペタスが減り、落下に伴ってインペタスが増加し、ますます速く落ちるようになる、と説明した。)ガリレイは、当初、このインペタス理論を採用していた[2]が、やがてガリレイは物体の運動をモメント(重さ以外の、距離や速度などをひとまとめに呼ぶ、ガリレオによる概念)という考え方で理解しはじめ[2]、(内部要因の変化で説明する)インペタス理論は採らなくなった[2]。では落下速度はどのような理屈で増加するのか? 落下距離に比例するか? 落下時間に比例するか? という点で、(経緯が詳しくは分かってはいないらしいが)1600年ごろガリレイは悩み悪戦苦闘したらしい[2]が、1604年には「落下速度は時間に比例する」という仮説にたどり着いた[2]、という。こうしてガリレイは動力学に貢献した[2]。ガリレイは斜面で球を転がす実験を多数行い、水平面では等速になることから、「加速・減速の外的原因が取り去られている限り、いったん運動体に与えられたどんな速度も不変に保たれる」という考え方をするようになった[2]。これは現代で言う慣性の法則に近いものではあるが、ただガリレイは、それは地上の物体にだけ通用する法則であって、天体には通用しないと考えていた[2]。ガリレイも古代ギリシャ以来の考え方をなぞり、天体は天体で別の性質を持っている、円運動をする性質を持っているのだ、と考えていたのである[2]。
ニュートン、フック、ハリーらの活動[編集]
アイザック・ニュートンの肖像画
ニュートンの発想 ~ガリレオ動力学の天体への適用~[編集]
一般には、アイザック・ニュートン(1642-1727)が1665年に、地上の引力が月などに対しても同様に働いている可能性があることに気付いた、とされている。
スタックレーの著書『回想録』には、スタックレーが、ニュートンが死去する前年の4月15日にロンドン西方の彼の自宅を訪問した時、昼食をともにしたあと庭に出て数本のりんごの木陰でお茶を飲んでいたところ、話の合間にニュートンが「昔、万有引力の考えが心に浮かんだ時とそっくりだ。瞑想にふけっていると、たまたまりんごが落ちて、はっと思いついたのだ」と語った、と書いてあるという[2]。(ただし、りんごの逸話はしばしば伝説ともされることもあり、内容の真偽のほどは確かではない。)
同時期の、フックによる引力に関する活動[編集]
ロバート・フックの近年[いつ?]の想像画。1665年に引力を論じ、1666年に王立協会で引力に関する講演を行い、1679年には引力に関する意見を求める手紙をニュートンに送った。(存在したはずの唯一の肖像画は、その後ニュートンとの確執の中で失われたと推測されている)
ロバート・フックは1665年の『顕微鏡図譜』まず、月に対して何の力も働かなければ、月はガリレオの慣性の考え方によれば直線方向にAからBまで1分間に37.4km進む、と計算される。(月を円軌道とし、地球一周に27日7時間43分かかることから算出)。だが、月はBではなくB´の位置にいる。つまり1分間にBB´だけ「落下する」と考えることができる。その長さは直角三角形AOBにピタゴラスの定理を用い計算でき、毎分4.9mの落下、となる。毎秒ならば、その3600分の1、4.9/3600となる。ところで地上の落下は、ガリレイが見出した法則により、毎秒4.9mである。月の位置で働く引力は、地球上の3600分の1まで弱まっている、ということになる。月までの距離は地球半径の60倍だから、結局、この引力というのは距離の2乗に反比例しているということになる(逆2乗の法則)。[2]引力の法則を論じた。フックは1666年に王立協会において "On gravity"(引力について)と題して講演をし、移動する物体は何らかの力を受けない限りそのまま直進すること(慣性の法則)および引力は距離が近いほど強くなる、という法則を追加した、とされる。またフックは、1666年に王立協会と交わした書簡において、世界のしくみについて次の3点を述べたと、ダガルド・スチュワート(Dugald Stewart)は自著 Elements of the Philosophy of the Human Mindにおいて指摘している[3]。
全ての天体は引力(gravity)によってその各部分を中心に引きつけているだけでなく、天体間で相互に引き付けあって運動する。
外部から力が継続的に加わらない限り、天体は単純に直進し続ける。しかし、引力によって天体は円軌道、楕円軌道などの曲線を描く。
この引力は天体同士が近いほど強くなる。距離と引力の強さの関係がどうなっているか、今のところ私にも発見できていない。
1679年のこと、アイザック・ニュートン(1642-1727)のもとに、王立学会の書記ロバート・フック(1635-1703)から、1679年11月24日付けの手紙が届いた。「惑星の運動に関する私の仮説について、あなたの意見を学会機関紙に投稿してほしい」というものだった[2]。ニュートンは当時、光学の研究に忙しくて、フックがその5年前に惑星の運動を説明するための仮説を学会に提出していたことも知らなかった[2]という。当時、惑星の運動については、ケプラーが観測値によって算出した三つの法則があることは、学者たちには知られていた。第一法則 - 惑星は太陽を焦点とした楕円軌道を描く[2]。第二法則 - 惑星は太陽に近い軌道では速く、遠いところではゆっくり動き、惑星と太陽とを結ぶ直線が等しい時間等しい面積を掃くように動く(面積速度一定の法則)[2]。第3法則 - 惑星が太陽を一周する時間(周期)の2乗は、惑星と太陽との平均距離の3乗に比例する[2]。
では、なぜ惑星はこのような動き方をするのか? 当時の自然哲学者たちは、ガリレイたちが作り上げてきた地上の動力学を使おうと考えるようになっていた[2]という。ガリレイは、外力が働かなければ地上の物体は等速直線運動をつづける、という考え方をしていた。ところが惑星が直線ではなく楕円を描くということは、太陽の方向に働く引力がある、ということになる[2]という。
フックが手紙でニュートンに意見を求めた点は、この楕円運動を作り出す、太陽に引き寄せる力、引力についてであり、この引力がどのような性質のものか?という点であった[2]という。この手紙を見てニュートンは13年ほど前にウールソープ(ニュートンの家)で試してみた、地上の重力が月にまで及んでいると想定して行った計算、をやり直してみることにした[2]という。
それは例えばおよそ次のようなものであった。
まず、月に対して何の力も働かなければ、月はガリレオの慣性の考え方によれば直線方向にAからBまで1分間に37.4km進む、と計算される。(月を円軌道とし、地球一周に27日7時間43分かかることから算出)。だが、月はBではなくB´の位置にいる。つまり1分間にBB´だけ「落下する」と考えることができる。その長さは直角三角形AOBにピタゴラスの定理を用い計算でき、毎分4.9mの落下、となる。毎秒ならば、その3600分の1、4.9/3600となる。ところで地上の落下は、ガリレイが見出した法則により、毎秒4.9mである。月の位置で働く引力は、地球上の3600分の1まで弱まっている、ということになる。月までの距離は地球半径の60倍だから、結局、この引力というのは距離の2乗に反比例しているということになる(逆2乗の法則)。[2]
ところでホイヘンスによる振り子の研究は、1659年ころの円運動の研究と結び付き、そこでの中心の引力というのは半径に比例し、周期の2乗に反比例する、ということが判り、これが1673年の『振子時計』で公表されたので、これとケプラーの第三法則を結びつければ、引力は半径の2乗に反比例する、ということはたやすく算出できるようになっていた[2]。
エドモンド・ハリー。ニュートンの体系を出版するように応援し続けた。
1684年1月のある水曜日[2]、ロンドンのコーヒーハウスにあつまったロバート・フック、天文学者エドモンド・ハリー、王立学会会長兼建築家クリストファー・レンは、残る問題となった、逆2乗の引力をもとにして、いかにケプラーの第一、第二法則を導くことができるか、ということを話題にした[2]。同年8月、ニュートンを大学で訪問したハリーは、ニュートンがすでに独自にこの問題を解決していたことを知り、11月に、それを出版することをすすめ、『自然哲学の数学的諸原理』の核心部分が出来てゆくことになった[2]。
フックは、引力については自分がニュートンに教えたのだとし、二人の間で対立が生じることになった。
その後ハリーが資金面で貢献してくれたり、あるいはフックとの先取権をめぐるいざこざの仲裁を行ってくれたお陰もあって、ニュートンはそれの刊行にこぎつけることができたのであった[2]という。
『自然哲学の諸原理』における、万有引力という考え方の公表[編集]
ニュートン自身が所有していたプリンキピアの初版。
ニュートンは成果を『自然哲学の数学的諸原理』(プリンキピア)にまとめあげ、それは1687年に刊行された。同書は全三篇構成であるが、惑星の運動が主として扱われているのは第三篇の「世界体系について」である[2]。例えば、「月は地球に向かって重力で引かれる」という、ニュートンがウールスソープ時代に思いついた命題は、第三篇の命題4において提示されており、逆2乗の引力が木星とその衛星、5つの惑星と太陽の間でも働くことを、ケプラーの第二・第三法則からこの引力を逆に導き出しつつ主張した[2]。さらに命題7で、重力は物の量(質量)に比例することを述べ、それにより、第三篇の命題8において、この宇宙ではどこでも、物質には互いに物質の量の積に比例する逆二乗の引力が働いている、と主張した[2]。つまり万有引力の法則があると主張したわけである[2]。
ニュートン力学と重力[編集]
古典力学
\boldsymbol{F} = \frac{\mathrm{d}}{\mathrm{d}t}(m \boldsymbol{v})
運動の第2法則
歴史(英語版)
[表示]分野
[表示]定式化
[表示]基本概念
[表示]主要項目
[表示]科学者
表・話・編・歴
ニュートンは『自然哲学の数学的諸原理』において自らの力学体系を開示したわけである。この力学体系をニュートン力学という。
ニュートン力学そのままの用語では、現代では理解しにくい点もあるので、以下では、古典力学の現代版の用語や記述方式を用いつつ、万有引力を解説する。
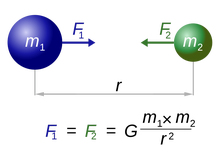
ニュートンは、太陽を公転する地球の運動や木星の衛星の運動を統一して説明することを試み、ケプラーの法則に、運動方程式を適用することで、万有引力の法則(逆2乗の法則)が成立することを発見した。これは、『2つの物体の間には、物体の質量に比例し、2物体間の距離の2乗に反比例する引力が作用する』と見なす法則である。力そのものは、瞬時すなわち無限大の速度で伝わると考えた。式で表すと、万有引力の大きさFは、物体の質量を M,m 、物体間の距離を r として、
F= G \frac{M m}{r^2}
となる。Gは万有引力定数と呼ばれる比例定数で、
G = 6.67259 \times 10^{-11} \mbox{m}^3 \cdot \mbox{s}^{-2} \cdot \mbox{kg}^{-1}
である。(因みに「この式が全ての物体の間で成立する」と考えると「木から落ちるリンゴにも適用することができる」と考えることができるのである。)
地球の質量を M 、リンゴの質量を m 、地球の半径を R とすれば、万有引力の大きさは、 F= G \frac{M m}{R^2} であり、リンゴの運動方程式は、加速度を g として、 mg= G \frac{M m}{R^2} となる。すなわち、地球重力による加速度(重力加速度)は
g=\frac{G M}{R^2}
となり、すべての物質について同じ値になる。
地球表面では重力加速度は約9.8m/s2であり、地球の半径は約6400kmであるので、上記の式から地球の質量を
M=\frac{g R^2}{G} \simeq 6 \times 10^{24} kg
のように求めることができる。同様に、他の惑星上での重力加速度も求めることができる。
ありがちな誤解[編集]
ちなみにニュートンによる「万有引力の法則の発見」を“重力の発見”だと解釈してしまう例があるが、これは間違った解釈である。「リンゴが木から落ちるのを見て、ニュートンは万有引力を発見した」などとする、単純化された、巷に流布している逸話も、この誤解を広める原因になっている可能性がある。ニュートンは「リンゴに働く重力」を発見したわけではない。「リンゴに対して働いている力が、月や惑星に対しても働いているのではないか」と着想したのである。地上では物体に対して地面(地球)に引きよせる方向で外力が働くことは、(ガリレオなどの貢献もあり)ニュートンの時代には理解されていた。ニュートンが行った変革というのは、同様のことが天の世界でも起きている、つまり宇宙ならばどこでも働いている、という形で提示したことにある(そして同時に、地球が物体を一方的に引くのではなく、全ての質量を持つ物体が相互に引き合っている事と、天体もまた質量を持つ物体のひとつに過ぎない事)。「law of universal gravitation 万有引力の法則」という表現は、それを表している。
評価[編集]
万有引力の考え方は大きな議論・非難を呼んだ。同著発表当時、物体の運動の説明というのは、ヨーロッパ大陸側であれイギリス側であれ、近接作用論で考えられていた。プリンキピアはそれに対して異論を唱える形で万有引力という遠隔作用論を大々的に提示した形になった。
「渦動説」および「重力を説明する古典力学的理論」も参照
これはライプニッツおよびその一派らから反発を呼び、「オカルト的な質を持ち込んでいる」「オカルト的な力を導入している」と非難されることになった。大陸側の学者らはライプニッツの考え方を支持していたので、ドーバー海峡を隔てて大陸側の学者たちと議論が数十年以上も続くことになった。ニュートンは『自然哲学の数学的諸原理』の第二版発行の時点では同版に「Hypotheses non fingo (我、仮説を立てず)」との記述を書き加えた[4]。
もっとも、第二版にHypotheses non fingoとは書いたものの、ニュートン自身は実際にはその後、万有引力が起きる仕組みについての検討・考察を行っており、重力というのはエーテルの流れが引き起こしているのかも知れない、とも考察した[5]。すなわち近接作用論に回帰するような仮説立て、推察も行っていたのである。[6]
現代の初学者向けの科学史などでは、こうした複雑な経緯がすっかり忘れ去られ美化され、「ニュートンは原因の哲学的な思弁を避け、数的な関係の記述にとどめるという新しい方法論を提唱した」「力学の基礎、ひいては近代科学の考え方の基礎となった」とだけ解説がされていることもある。
万有引力の法則、その後[編集]
イギリス側の自然哲学者はニュートンの説を支持をする者が多かったが、その後、数十年以上の長い年数の議論を経て徐々に大陸側でも支持者が増え、やがては物理学においては自然界に存在する基本的な力だと見なされるようになっていった。
後の時代で発見された電磁気力では、引力と斥力がある、とされているのに対して、重力(万有引力)では引力しか存在せず、斥力は存在しない。
現在では、重力と呼ぶ場合には、質量に加速度を与える力全般を意味する。重力には、地球自転の遠心力のような慣性の力や、一般相対論で予言される慣性系の引きずりによる力も含まれるが、それらは万有引力ではない[要出典]。
重力(または重力相互作用)の正体は、アルベルト・アインシュタインの一般相対性理論では、質量を持つ物体が引き起こす時空の歪みである、と説明された。これに対して、'万有引力'という用語は、ニュートンの定式化した重力の意味で用いられる傾向にある。[要出典]
今日、質量を有する任意の2物体が引力の相互作用ポテンシャルを伴うことは、疑いのない自然法則として認められているが、その理由や機構についての研究は進んでいないという状況にあると言える。
一般相対性理論と重力[編集]
アインシュタインは、光速度に近い場合の力学として、1905年に特殊相対性理論を発表した後、加速度運動を含めた相対性理論の構築に取り掛かかった。そして重力場を時空の幾何学として取り扱う方法を模索し、1916年に一般相対性理論を発表した。
アインシュタインの重力場の方程式(アインシュタイン方程式)では、万有引力はもはやニュートン力学的な力ではなく、重力場という時空の歪みである、と説明されるようになった。また、重力の作用は、瞬時ではなく光速度で伝えられる、とされるようになった。
ニュートンの万有引力の法則では、質量を持った物体間の力であるとされるので、質量を持たない物質には万有引力は存在しない事となる。[要出典] 一般相対性理論では、重力が時空の歪みであるとするため、光の軌道もまた重力によって曲がる事を意味する。これはアーサー・エディントン による観測で実証されることになった。
一般相対性理論は、非常に強い重力が働く場を記述する。[要出典] 太陽系であれば、ニュートン力学に若干の補正項が加わる程度なので、ニュートン力学はその意味で近似的に正しいと考えて差し障りない。例えば前述の光の軌道の歪みについても、太陽の近傍においてようやく観測され得るものである。 アインシュタイン方程式は、通常の物理の方程式と同様、時間反転に対して対称なので、宇宙全体に適用すると、重力の影響で収縮宇宙の解と共に、膨張宇宙の解が得られる[要出典]、という。
一般相対性理論の発表当時は、ハッブルによる膨張宇宙の発見前で、アインシュタインは「宇宙は静的で安定している」と考えていた。自身の方程式が、動的な宇宙を予言したため、アインシュタインは万有引力に拮抗する万有斥力があると想定し、重力場の方程式に宇宙項を加えることで、静的な解が存在できるように重力場の方程式を修正した。
後に彼は宇宙項を「生涯最大の過ち」と悔いた。
「だが、宇宙項のアイデアは現在の宇宙論では、宇宙のインフレーションや宇宙の加速膨張を説明するものとして復活していると言える[要出典]」と言う。
「相対性理論」も参照
素粒子物理学と重力[編集]
素粒子物理学では、自然界に存在する四つの基本的な相互作用のひとつとして、素粒子間に働く重力相互作用とみなされ、重力子(グラヴィトン)という素粒子により媒介するとみなされるが、素粒子としての重力子は現在のところ未発見である。素粒子間の重力相互作用は無視できるほど小さいが、素粒子と地球との間の重力を考慮する必要があることもある。[要出典]
(※「ひとつの原子に存在する電子の数と陽子の数は同じで、種類によって数が決まっている。により、やはり電荷を帯びた電子が運動する事により電磁波が生まれ、それが引き付けあう力(反発力より若干大きい為)が発生し引力として認識される[要出典]、とする説もある。)
量子重力[編集]
近年では、量子力学と一般相対性理論の結合、重力の量子化が試みられ、量子重力と呼ばれている。格子重力などさまざまな試みがあるが、実現は困難である。量子重力を宇宙論に適用する試みは、量子宇宙論と呼ばれる。
出典[編集]https://ja.wikipedia.org/wiki/%E4%B8%87%E6%9C%89%E5%BC%95%E5%8A%9B
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 275: The division by zero $z/0=0$ and special relative theory of Einstein
}
\author{{\it Institute of Reproducing Kernels}\\
\date{January 11, 2016}
\maketitle
{\bf Abstract: } In this announcement, for its importance, we will state a fundamental result for special relative theory of Einstein from the division by zero $z/0=0$.
\bigskip
{\bf Introduction}
\bigskip
%\label{sect1}
By {\bf a natural extension of the fractions}
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, the division by zero
\begin{equation}
\frac{b}{0}=0,
\end{equation}
is clear and trivial. See (\cite{msy}) for the recent results. See also the survey style announcements 179,185,237,246,247,250 and 252 of the Institute of Reproducing Kernels (\cite{ann179,ann185,ann237,ann246,ann247,ann250,ann252}). The division by zero is not only mathematical problems, but also it will give great impacts to human beings and the idea on the universe. The Institute of Reproducing Kernels is presenting various opinions in Announcements (many in Japanese) on the universe.
In this Announcement, for its importance, we will state a fundamental result for special relative theory of Einstein from the division by zero $z/0=0$. The contents were stated by Hiroshi Michiwaki in his memo dated on October 10, 2014 and we should state the results, more early.
\section{Special relative theory of Einstein}
Einstein's discovery of the equivalence of matter/mass and energy \cite{ein} in the year 1905 lies
at the core of today's modern physics. According to Albert Einstein \cite{einstein}, the rest-mass $m_0$, a
measure of the inertia of a (quantum mechanical) object is related to the relativistic mass $m_R$
by the equation, with relative velocity $v$ and the speed $c$ of light in vacuum,
\begin{equation}
m_0 = m_R \sqrt{1 - \frac{v^2}{c^2}}.
\end{equation}
Therefore, we obtain, immediately
\begin{equation}
m_R^2= m_0^2 \left(1 - \frac{v^2}{c^2}\right)^{-1}.
\end{equation}
Therefore, by the division by zero, we have the surprising result for $ v = c$:
\begin{equation}
m_R = 0.
\end{equation} It seems that the modern physical common sense is then $
m_R = + \infty$.
\bigskip
\section{ A conjecture by H. Michiwaki}
As his simple result (1.3) from the division by zero, Michiwaki stated his conjecture or interpretation for neutrino; neutrino are able to have small mass, because they are moved with near $c$ or $c$ velocity.
Indeed, we assume that $m_0$ is the mass of neutrino at the stopped case. As the experiment, we know that the velocity of neutrino is near to $c$ or $c$. So he thought
that neutrino will have small mass.
This result was realized positively by Takaaki Kajita by experiment and he got Novel Prize in 2015.
Furthermore, he referred to the very interesting interpretations of {\it photon of energy} and {\it Doppler effect} from the viewpoint of the division by zero in his memo.
\section{Acknowledgements}
This announcement was, of course, inspired by the paper \cite{bb} and for the very interesting relation with computer sciences and the division by zero, see \cite{bht}.
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{bb}
Barukcic J. P., and I. Barukcic, Anti Aristotle - The Division Of Zero By Zero,
ViXra.org (Friday, June 5, 2015)
© Ilija Barukčić, Jever, Germany. All rights reserved. Friday, June 5, 2015 20:44:59.
\bibitem{bht}
Bergstra, J. A., Hirshfeld Y., and Tucker, J. V.,
Meadows and the equational specification of division (arXiv:0901.0823v1[math.RA] 7 Jan 2009).
\bibitem{cs}
Castro, L. P., and Saitoh, S. (2013).
Fractional functions and their representations. {\it Complex Anal. Oper. Theory {\bf7}, no. 4, }1049-1063.
\bibitem{ein}
Einstein, A. (1905) Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?, Annalen der Physik, vol. 323, Issue 13, pp. 639-641,
\bibitem{einstein}
Einstein, A. (1905).
Zur Elektrodynamik bewegter Körper, Annalen der Physik, vol. 322, Issue 10, pp. 891-921.
\bibitem{kmsy}
Kuroda, M., Michiwaki, H., Saitoh, S., and Yamane, M. (2014).
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
{\it Int. J. Appl. Math. Vol. 27, No 2 }, 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msy}
Michiwaki H., Saitoh S., and Yamada M. (2015).
Reality of the division by zero $z/0=0$. IJAPM (International J. of Applied Physics and Math. (to appear).
\bibitem{mst}
Michiwaki, H., Saitoh, S., and Takagi, M.
A new concept for the point at infinity and the division by zero z/0=0
(manuscript).
\bibitem{s}
Saitoh, S. (2014).
Generalized inversions of Hadamard and tensor products for matrices,
{\it Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 , 87-95.} http://www.scirp.org/journal/ALAMT/
\bibitem{taka}
Takahasi, S.-E. (2014).
{On the identities $100/0=0$ and $ 0/0=0$.}
(note)
\bibitem{ttk}
Takahasi, S.-E., Tsukada, M., and Kobayashi, Y. (2015).
{\it Classification of continuous fractional binary operations on the real and complex fields. } Tokyo Journal of Mathematics {\bf 8}, no.2(in press).
\bibitem{ann179}
Division by zero is clear as z/0=0 and it is fundamental in mathematics. {\it Announcement 179 (2014.8.30).}
\bibitem{ann185}
The importance of the division by zero $z/0=0$. {\it Announcement 185 (2014.10.22)}.
\bibitem{ann237}
A reality of the division by zero $z/0=0$ by geometrical optics. {\it Announcement 237 (2015.6.18)}.
\bibitem{ann246}
An interpretation of the division by zero $1/0=0$ by the gradients of lines. {\it Announcement 246 (2015.9.17)}.
\bibitem{ann247}
The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$. {\it Announcement 247 (2015.9.22)}.
\bibitem{ann250}
What are numbers? - the Yamada field containing the division by zero $z/0=0$. {\it Announcement 250 (2015.10.20)}.
\bibitem{ann252}
Circles and curvature - an interpretation by Mr. Hiroshi Michiwaki of the division by
zero $r/0 = 0$. {\it Announcement 252 (2015.11.1)}.
\end{thebibliography}
\end{document}
再生核研究所声明 264 (2015.12.23): 永遠とは何か ― 永遠から
現代人は 空間とは 座標軸で表される数の組の集合 で表させるものと発想しているだろう。 基礎である直線は 実数を直線上に並べたもの、逆に直線とは 実は 実数全体の表現と考えられる。 すなわち、直線とは 基準点である原点ゼロから、正方向と負方向に正の実数と負の実数が大小関係で順序づけられ無限に双方向に伸びていると考えられる。
そこで、永遠とは 直線に時間を対応させ、限りなく正方向に進んだ先のことを 想像している。どこまでも どこまでも 先に行けばどうなるだろうか。直線上でも、平面上でも である。 砂漠の伝統を有する欧米文化の背景、キリスト教などの背後には、 永遠とは限りなく 果てしなく先にあると発想しているという。 どこまでも、どこまでも きりのない世界である。 ユークリッド幾何学が そのような空間を考えていることは確かである。
ところが四季に恵まれたアジアの民は、限りなく広がる世界に、不安や淋しさを直感して、 正の先と、負の先が一致していて、直線は円で どこまでも どこまでも行くと反対方向から、現在に至り、永遠は繰り返しであると、四季の繰り返し、天空の繰り返し、円運動のように発想して 仄かな安心感を覚えているという。永劫回帰、輪廻の思想を深く懐いている。実に面白いことには 美しい複素解析学では、立体射影の考えによって、直線を球面上の円と表現し、無限遠点の導入によって、 これらの思想を 数学的に厳格に実現させ、全ユークリッド平面の全貌を捉え、無限の彼方さえ捉えることが出来た。 その時 永遠を 確かに捉え、掴むことさえ出来たと言える。立体射影による球面上の北極に 確かに存在すると言える。素晴しい、数学を手に入れていた。この美しい数学は 100年以上もリーマン球面として、複素解析学の基本となってきている。
ところが2014.2.2偶然に発見されたゼロ除算の結果は、この無限遠点が 実は原点に一致していた という衝撃的な事実を述べていた。 永遠、無限の彼方と想像していたら、それが 実は原点に戻っていたという事実である。 それが我々の数学であり、ユークリッド空間の実相である。幾何学の性質や物理的な法則をきちんと説明している、我々の世界の数学である。
それで、永遠や無限遠点、我々の空間の 十分先の考え方、発想を考える必要がある。
無限の先が原点に一致している事実、それを如何に理解すべきであろうか。
それについて、 次のように解説してきた:
再生核研究所声明232(2015.5.26)無限大とは何か、無限遠点とは何か。― 驚嘆すべきゼロ除算の結果
再生核研究所声明257 (2015.11.05) 無限大とは何か、 無限遠点とは何か ー 新しい視点
再生核研究所声明262 (2015.12.09) 宇宙回帰説 ― ゼロ除算の拓いた世界観
新しい世界観は 始まりから始まり 最後には 突然戻るということを述べている。 しからば、始めとは何で 終りとは何だろうか。 これについて、 始めも終わりも、質的な変化であると定義できるのではないだろうか。 簡単な数学で万物、universe の現象を説明するのは難しい状況は確かにあるだろう.しかし、ゼロ除算の思想は、新羅万象が絶えず変化して 繰り返している様を表現しているように感じられる。
大事な人生の視点は 今日は 明日のためや遠い未来のためにあるのではなく、 現在、現在における在るべき適切な在りようが大事だと言っているようである。もちろん、現在は、未来と過去に関係する存在であり、それらは関係付けられ、繋がっているが 焦点はもちろん、 現在にあるということである。
ビッグバンの宇宙論は 適切に理解され、始めとは 大きな変化で 現状の元が始まり、
やがて突然、元に戻って 終わることを暗示しているようである。人生とは 要するに 内なる自分と環境に調和するように在れ と ゼロ除算は言っているようである。
ゼロ除算は 仏教の偉大なる思想 を暗示させているように感じられる。
以 上
Reality of the Division by Zero z/0 = 0
http://www.ijapm.org/show-63-504-1.html
http://okmr.yamatoblog.net/
再生核研究所声明262 (2015.12.09) 宇宙回帰説 ― ゼロ除算の拓いた世界観
最近展開しているゼロ除算が、新しい世界観を示しているのは 大変興味深い。直線とは一体どうなっているだろうか.空間とはどのようになっているだろうか。これについて、現代人は、双方向にどこまでも どこまでも 続いている直線を想像するであろう。限りなく広がった平面や空間である。ところが 立体射影によって 平面全体を球面上に1対1に写せば、全平面は 球面から北極を除いた球面上に1対1にきちんと写るから、無限に広がる 全平面の全貌が捉えられる。ところが平面上には存在しない想像上の点 それはあらゆる方向に限りなく遠くに存在する無限遠点の導入によって、その点を球面の欠けた1点北極に対応させれば、無限遠点を含めた平面全体は 球面全体と1対1にきちんと対応する。
このような対応で 平面上の円や直線全体は 球面上では共に円に対応するという美しい対応になり、平面上の直線は 球面上では、北極(無限遠点)を通る円に写ると、直線と円の区別は 球面上では不要になる。また、平面上の平行線とは 無限遠点で 角度ゼロで交わっている(接している)と平面上の構造がよく見えて、無限遠点を含めての平面の全構造が 捉えられる。このように、考えると、直線とは、球面上では北極を通る円、平面上では無限遠点を通る直線となる。この構造は、直線を1方向にどこまでも, どこまでも進めば、無限遠点を 通って、逆方向から戻ってくるという、永劫回帰の思想をちょうど実現している。それは、球面上では、 円を繰り返し回ることを意味する。 その様は 何もかも すっかり良く見える。
これが、従来100年以上も続いた世界観で、関数y=x やW=zは 無限遠点に近づけば、それらの像も無限遠点に近づいていると考えるだろう。 関数y=x の値は正方向にどんどん行けば、どんどん大きくなると考えるだろう。
しかるに、ゼロ除算1/0=0は、それらの関数は無限遠点にいくらでも近づくと 無限遠点にいくらでも近づくが、無限遠点自身では、突然ゼロになっていることが 幾何学的にも確認された。上記、北極は 実は原点ゼロに一致しているという。
話しを簡単にするために、 関数y=x を考えよう。右に行けば、プラス無限に、負の方向左に行けば 負の無限に限りなく近づくは 従来通りである。ところが、ゼロ除算では いずれの方向でも上記無限遠点では 値ゼロをきちんと取っているという。ゼロ除算の数学では、どんどん、増加した先、突然、ゼロ、原点に戻っているという。また、円でも球面でも半径Rをどんどん大きくすると、当然、円の面積や球の体積はどんどん限りなく大きくなるが、半径が無限のとき、突然、それらはゼロになるという。それらの理由も数学ばかりではなく、幾何学的にも明確に見えている。
この数学的な事実は、我々の世界、宇宙がどんどん拡大して行くと突然、ゼロに帰するということを暗示させている。 ― これは 宇宙回帰説を意味しているようである。
これは、ユニバースの普遍的な現象、どんどん進んだ先が、元に突然戻る原理を示しているようである。
そもそも人生とは如何なるものか。― よくは分からないが、事実として、生まれて、どんどん物心がついて、人間として精神活動が活発化して、多くは本能原理によって生かされて、そして、突然元に戻ることを意味しているようである。このことを深く捉えられれば、世界がよりよく観え、悟りの境地に達する大きなヒントを得ることができるだろう。
ここでは ゼロ除算の帰結として、宇宙回帰説、ユニバースの回帰説を唱えたい。この考えでは、どんどん進めば、突然元に戻るという原理を述べている。珠算における 御破算で願いましては で 再び始めることを想起させる。これは、また、reset と同様であると考えられる。
以 上
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
https://notevenpast.org/dividing-nothing/
割り算のできる人には、どんなことも難しくない
世の中には多くのむずかしいものがあるが、加減乗除の四則演算ほどむずかしいものはほかにない。
ベーダ・ヴェネラビリス
数学名言集:ヴィルチェンコ編:松野武 山崎昇 訳大竹出版1989年
Reality of the Division by Zero z/0 = 0
http://www.ijapm.org/show-63-504-1.html
http://okmr.yamatoblog.net/










曖昧さ回避 日本の劇団については「演劇実験室◎万有引力」をご覧ください。
万有引力(ばんゆういんりょく、英語: universal gravitation)または万有引力の法則(ばんゆういんりょくのほうそく、英語: law of universal gravitation)とは、「地上において質点(物体)が地球に引き寄せられるだけではなく、この宇宙においてはどこでも全ての質点(物体)は互いに gravitation(=引き寄せる作用、引力、重力)を及ぼしあっている」とする考え方、概念、法則のことである。
目次 [非表示]
1 歴史
1.1 前史
1.1.1 アリストテレスの考え方
1.1.2 中世の考え方
1.1.3 地上の範囲での、従来の自然学への疑念と改良
1.2 ニュートン、フック、ハリーらの活動
1.2.1 ニュートンの発想 ~ガリレオ動力学の天体への適用~
1.2.2 同時期の、フックによる引力に関する活動
1.3 『自然哲学の諸原理』における、万有引力という考え方の公表
2 ニュートン力学と重力
3 ありがちな誤解
4 評価
5 万有引力の法則、その後
5.1 一般相対性理論と重力
5.2 素粒子物理学と重力
5.3 量子重力
6 出典
7 関連項目
歴史[編集]
前史[編集]
この万有引力という見方がどのようなものであるか、その正しい位置づけ・真価を理解するには、一旦、この概念が生み出される以前に人々がこの世界をどのようにとらえていたのか、その考え方、世界の見え方(世界観)に寄り添って理解し、そこからどのように変えていったのか、その相違の程度を理解する必要がある。
アリストテレスの考え方[編集]
石を手から離せば自然に地面へと落ちる。古代ギリシャの哲学者アリストテレスは、その原因は、石を構成する土元素(四元素のうちの一つ)が、本来の位置である地へ戻ろうとする性質にあると考えた[1]。土元素が多いものが重い、と考え、それが多いものほど速く落ちる、と考えた[2]。
中世の考え方[編集]
中世ヨーロッパではアリストテレスの考え方が広く知られていたので、人々はそうした見方で世界を見ていた。以下のような考え方である。
我々人間は、それぞれの家に住んでいる。人間は何かの理由で家から離れることがあっても、結局はその家に帰ろうとする。動物も同じだ。地リスは地面に巣穴を持っている。何かの理由があると、たとえば危険を感じると、穴から一時的に離れることはあるが、危険がさればやはりその巣穴に戻ろうとする。鳥もそうだ。鳥も何かの理由、例えば食べ物を探すために一時的に巣から飛び立つことがあるが、結局はその巣へ帰ってくる。命あるものは全て、それぞれの性質に応じて本来の位置というものをもっていて、一時的にそこから離れることはあっても、結局はそこへ帰ろうとするものだ[1]。
生き物がそれぞれ本来の位置というのを持っているように、物(無生物)も、それぞれの性質に応じて本来の位置を持っている。たとえば小石はその本来の位置を地に持っている。焔はその本来の位置を天上に持っている[1]。
例えば、小石を空中に投げれば、小石は本来の位置から離されることになり、小石は一旦は抵抗を示しながら上に上がるが、結局はできるだけすみやかに、その本来の位置である地に戻ってこようとする[1]。
だが、無生物でも、その本来の位置を持たないと思われる存在がある。天に見える天体である。天体は永久に同じ運動を繰り返すばかりで、その本来の位置を持っていないように見える[1]。そこで中世の人々は、地上の存在と天の存在は本質的に異なっていると考え、地上の存在はただの存在であり、それに対して天の世界に属する存在、永遠に運動を繰り返す天体は、いわば霊的な存在である、と考えた[1]。中世の人々は、天の世界は地上とは全く別の法則が働いている別世界なのだ、と考えていたのである。また、天の世界の、地上とは異なった性質を説明するために、地上は四元素でできているのに対して、天体は第五元素でできている、とも考えていた。
地上の範囲での、従来の自然学への疑念と改良[編集]
さて、アリストテレスの考え、「土元素が多いものが重い、それが多いものほど速く落ちる」については、パドヴァ大学のベネデッティ(Giambattista Benedetti、1530-1590)が異論を唱えた[2]。またオランダのステヴィン(Simon Stevin、1548-1620)は、重さが10倍異なる二つの鉛玉を9メートルほど落下させ、ほとんど同時に落ちることを確かめて、このアリストテレスの理論に異議を唱えた[2]。
自然学者ガリレオ・ガリレイ(1564-1642)も、上記の中世の考え方(の一部)に疑問を投げかけた[1]。(ところで、先行する14世紀の自然学者ビュリダンはインペタス理論(いきおい理論)を提唱し、その理論では、物体を投げると手からインペタスが物体の内部に移ることで飛び続け、空気や重さなどの抵抗により内部要因のインペタスが減り、落下に伴ってインペタスが増加し、ますます速く落ちるようになる、と説明した。)ガリレイは、当初、このインペタス理論を採用していた[2]が、やがてガリレイは物体の運動をモメント(重さ以外の、距離や速度などをひとまとめに呼ぶ、ガリレオによる概念)という考え方で理解しはじめ[2]、(内部要因の変化で説明する)インペタス理論は採らなくなった[2]。では落下速度はどのような理屈で増加するのか? 落下距離に比例するか? 落下時間に比例するか? という点で、(経緯が詳しくは分かってはいないらしいが)1600年ごろガリレイは悩み悪戦苦闘したらしい[2]が、1604年には「落下速度は時間に比例する」という仮説にたどり着いた[2]、という。こうしてガリレイは動力学に貢献した[2]。ガリレイは斜面で球を転がす実験を多数行い、水平面では等速になることから、「加速・減速の外的原因が取り去られている限り、いったん運動体に与えられたどんな速度も不変に保たれる」という考え方をするようになった[2]。これは現代で言う慣性の法則に近いものではあるが、ただガリレイは、それは地上の物体にだけ通用する法則であって、天体には通用しないと考えていた[2]。ガリレイも古代ギリシャ以来の考え方をなぞり、天体は天体で別の性質を持っている、円運動をする性質を持っているのだ、と考えていたのである[2]。
ニュートン、フック、ハリーらの活動[編集]
アイザック・ニュートンの肖像画
ニュートンの発想 ~ガリレオ動力学の天体への適用~[編集]
一般には、アイザック・ニュートン(1642-1727)が1665年に、地上の引力が月などに対しても同様に働いている可能性があることに気付いた、とされている。
スタックレーの著書『回想録』には、スタックレーが、ニュートンが死去する前年の4月15日にロンドン西方の彼の自宅を訪問した時、昼食をともにしたあと庭に出て数本のりんごの木陰でお茶を飲んでいたところ、話の合間にニュートンが「昔、万有引力の考えが心に浮かんだ時とそっくりだ。瞑想にふけっていると、たまたまりんごが落ちて、はっと思いついたのだ」と語った、と書いてあるという[2]。(ただし、りんごの逸話はしばしば伝説ともされることもあり、内容の真偽のほどは確かではない。)
同時期の、フックによる引力に関する活動[編集]
ロバート・フックの近年[いつ?]の想像画。1665年に引力を論じ、1666年に王立協会で引力に関する講演を行い、1679年には引力に関する意見を求める手紙をニュートンに送った。(存在したはずの唯一の肖像画は、その後ニュートンとの確執の中で失われたと推測されている)
ロバート・フックは1665年の『顕微鏡図譜』まず、月に対して何の力も働かなければ、月はガリレオの慣性の考え方によれば直線方向にAからBまで1分間に37.4km進む、と計算される。(月を円軌道とし、地球一周に27日7時間43分かかることから算出)。だが、月はBではなくB´の位置にいる。つまり1分間にBB´だけ「落下する」と考えることができる。その長さは直角三角形AOBにピタゴラスの定理を用い計算でき、毎分4.9mの落下、となる。毎秒ならば、その3600分の1、4.9/3600となる。ところで地上の落下は、ガリレイが見出した法則により、毎秒4.9mである。月の位置で働く引力は、地球上の3600分の1まで弱まっている、ということになる。月までの距離は地球半径の60倍だから、結局、この引力というのは距離の2乗に反比例しているということになる(逆2乗の法則)。[2]引力の法則を論じた。フックは1666年に王立協会において "On gravity"(引力について)と題して講演をし、移動する物体は何らかの力を受けない限りそのまま直進すること(慣性の法則)および引力は距離が近いほど強くなる、という法則を追加した、とされる。またフックは、1666年に王立協会と交わした書簡において、世界のしくみについて次の3点を述べたと、ダガルド・スチュワート(Dugald Stewart)は自著 Elements of the Philosophy of the Human Mindにおいて指摘している[3]。
全ての天体は引力(gravity)によってその各部分を中心に引きつけているだけでなく、天体間で相互に引き付けあって運動する。
外部から力が継続的に加わらない限り、天体は単純に直進し続ける。しかし、引力によって天体は円軌道、楕円軌道などの曲線を描く。
この引力は天体同士が近いほど強くなる。距離と引力の強さの関係がどうなっているか、今のところ私にも発見できていない。
1679年のこと、アイザック・ニュートン(1642-1727)のもとに、王立学会の書記ロバート・フック(1635-1703)から、1679年11月24日付けの手紙が届いた。「惑星の運動に関する私の仮説について、あなたの意見を学会機関紙に投稿してほしい」というものだった[2]。ニュートンは当時、光学の研究に忙しくて、フックがその5年前に惑星の運動を説明するための仮説を学会に提出していたことも知らなかった[2]という。当時、惑星の運動については、ケプラーが観測値によって算出した三つの法則があることは、学者たちには知られていた。第一法則 - 惑星は太陽を焦点とした楕円軌道を描く[2]。第二法則 - 惑星は太陽に近い軌道では速く、遠いところではゆっくり動き、惑星と太陽とを結ぶ直線が等しい時間等しい面積を掃くように動く(面積速度一定の法則)[2]。第3法則 - 惑星が太陽を一周する時間(周期)の2乗は、惑星と太陽との平均距離の3乗に比例する[2]。
では、なぜ惑星はこのような動き方をするのか? 当時の自然哲学者たちは、ガリレイたちが作り上げてきた地上の動力学を使おうと考えるようになっていた[2]という。ガリレイは、外力が働かなければ地上の物体は等速直線運動をつづける、という考え方をしていた。ところが惑星が直線ではなく楕円を描くということは、太陽の方向に働く引力がある、ということになる[2]という。
フックが手紙でニュートンに意見を求めた点は、この楕円運動を作り出す、太陽に引き寄せる力、引力についてであり、この引力がどのような性質のものか?という点であった[2]という。この手紙を見てニュートンは13年ほど前にウールソープ(ニュートンの家)で試してみた、地上の重力が月にまで及んでいると想定して行った計算、をやり直してみることにした[2]という。
それは例えばおよそ次のようなものであった。
まず、月に対して何の力も働かなければ、月はガリレオの慣性の考え方によれば直線方向にAからBまで1分間に37.4km進む、と計算される。(月を円軌道とし、地球一周に27日7時間43分かかることから算出)。だが、月はBではなくB´の位置にいる。つまり1分間にBB´だけ「落下する」と考えることができる。その長さは直角三角形AOBにピタゴラスの定理を用い計算でき、毎分4.9mの落下、となる。毎秒ならば、その3600分の1、4.9/3600となる。ところで地上の落下は、ガリレイが見出した法則により、毎秒4.9mである。月の位置で働く引力は、地球上の3600分の1まで弱まっている、ということになる。月までの距離は地球半径の60倍だから、結局、この引力というのは距離の2乗に反比例しているということになる(逆2乗の法則)。[2]
ところでホイヘンスによる振り子の研究は、1659年ころの円運動の研究と結び付き、そこでの中心の引力というのは半径に比例し、周期の2乗に反比例する、ということが判り、これが1673年の『振子時計』で公表されたので、これとケプラーの第三法則を結びつければ、引力は半径の2乗に反比例する、ということはたやすく算出できるようになっていた[2]。
エドモンド・ハリー。ニュートンの体系を出版するように応援し続けた。
1684年1月のある水曜日[2]、ロンドンのコーヒーハウスにあつまったロバート・フック、天文学者エドモンド・ハリー、王立学会会長兼建築家クリストファー・レンは、残る問題となった、逆2乗の引力をもとにして、いかにケプラーの第一、第二法則を導くことができるか、ということを話題にした[2]。同年8月、ニュートンを大学で訪問したハリーは、ニュートンがすでに独自にこの問題を解決していたことを知り、11月に、それを出版することをすすめ、『自然哲学の数学的諸原理』の核心部分が出来てゆくことになった[2]。
フックは、引力については自分がニュートンに教えたのだとし、二人の間で対立が生じることになった。
その後ハリーが資金面で貢献してくれたり、あるいはフックとの先取権をめぐるいざこざの仲裁を行ってくれたお陰もあって、ニュートンはそれの刊行にこぎつけることができたのであった[2]という。
『自然哲学の諸原理』における、万有引力という考え方の公表[編集]
ニュートン自身が所有していたプリンキピアの初版。
ニュートンは成果を『自然哲学の数学的諸原理』(プリンキピア)にまとめあげ、それは1687年に刊行された。同書は全三篇構成であるが、惑星の運動が主として扱われているのは第三篇の「世界体系について」である[2]。例えば、「月は地球に向かって重力で引かれる」という、ニュートンがウールスソープ時代に思いついた命題は、第三篇の命題4において提示されており、逆2乗の引力が木星とその衛星、5つの惑星と太陽の間でも働くことを、ケプラーの第二・第三法則からこの引力を逆に導き出しつつ主張した[2]。さらに命題7で、重力は物の量(質量)に比例することを述べ、それにより、第三篇の命題8において、この宇宙ではどこでも、物質には互いに物質の量の積に比例する逆二乗の引力が働いている、と主張した[2]。つまり万有引力の法則があると主張したわけである[2]。
ニュートン力学と重力[編集]
古典力学
\boldsymbol{F} = \frac{\mathrm{d}}{\mathrm{d}t}(m \boldsymbol{v})
運動の第2法則
歴史(英語版)
[表示]分野
[表示]定式化
[表示]基本概念
[表示]主要項目
[表示]科学者
表・話・編・歴
ニュートンは『自然哲学の数学的諸原理』において自らの力学体系を開示したわけである。この力学体系をニュートン力学という。
ニュートン力学そのままの用語では、現代では理解しにくい点もあるので、以下では、古典力学の現代版の用語や記述方式を用いつつ、万有引力を解説する。
ニュートンは、太陽を公転する地球の運動や木星の衛星の運動を統一して説明することを試み、ケプラーの法則に、運動方程式を適用することで、万有引力の法則(逆2乗の法則)が成立することを発見した。これは、『2つの物体の間には、物体の質量に比例し、2物体間の距離の2乗に反比例する引力が作用する』と見なす法則である。力そのものは、瞬時すなわち無限大の速度で伝わると考えた。式で表すと、万有引力の大きさFは、物体の質量を M,m 、物体間の距離を r として、
F= G \frac{M m}{r^2}
となる。Gは万有引力定数と呼ばれる比例定数で、
G = 6.67259 \times 10^{-11} \mbox{m}^3 \cdot \mbox{s}^{-2} \cdot \mbox{kg}^{-1}
である。(因みに「この式が全ての物体の間で成立する」と考えると「木から落ちるリンゴにも適用することができる」と考えることができるのである。)
地球の質量を M 、リンゴの質量を m 、地球の半径を R とすれば、万有引力の大きさは、 F= G \frac{M m}{R^2} であり、リンゴの運動方程式は、加速度を g として、 mg= G \frac{M m}{R^2} となる。すなわち、地球重力による加速度(重力加速度)は
g=\frac{G M}{R^2}
となり、すべての物質について同じ値になる。
地球表面では重力加速度は約9.8m/s2であり、地球の半径は約6400kmであるので、上記の式から地球の質量を
M=\frac{g R^2}{G} \simeq 6 \times 10^{24} kg
のように求めることができる。同様に、他の惑星上での重力加速度も求めることができる。
ありがちな誤解[編集]
ちなみにニュートンによる「万有引力の法則の発見」を“重力の発見”だと解釈してしまう例があるが、これは間違った解釈である。「リンゴが木から落ちるのを見て、ニュートンは万有引力を発見した」などとする、単純化された、巷に流布している逸話も、この誤解を広める原因になっている可能性がある。ニュートンは「リンゴに働く重力」を発見したわけではない。「リンゴに対して働いている力が、月や惑星に対しても働いているのではないか」と着想したのである。地上では物体に対して地面(地球)に引きよせる方向で外力が働くことは、(ガリレオなどの貢献もあり)ニュートンの時代には理解されていた。ニュートンが行った変革というのは、同様のことが天の世界でも起きている、つまり宇宙ならばどこでも働いている、という形で提示したことにある(そして同時に、地球が物体を一方的に引くのではなく、全ての質量を持つ物体が相互に引き合っている事と、天体もまた質量を持つ物体のひとつに過ぎない事)。「law of universal gravitation 万有引力の法則」という表現は、それを表している。
評価[編集]
万有引力の考え方は大きな議論・非難を呼んだ。同著発表当時、物体の運動の説明というのは、ヨーロッパ大陸側であれイギリス側であれ、近接作用論で考えられていた。プリンキピアはそれに対して異論を唱える形で万有引力という遠隔作用論を大々的に提示した形になった。
「渦動説」および「重力を説明する古典力学的理論」も参照
これはライプニッツおよびその一派らから反発を呼び、「オカルト的な質を持ち込んでいる」「オカルト的な力を導入している」と非難されることになった。大陸側の学者らはライプニッツの考え方を支持していたので、ドーバー海峡を隔てて大陸側の学者たちと議論が数十年以上も続くことになった。ニュートンは『自然哲学の数学的諸原理』の第二版発行の時点では同版に「Hypotheses non fingo (我、仮説を立てず)」との記述を書き加えた[4]。
もっとも、第二版にHypotheses non fingoとは書いたものの、ニュートン自身は実際にはその後、万有引力が起きる仕組みについての検討・考察を行っており、重力というのはエーテルの流れが引き起こしているのかも知れない、とも考察した[5]。すなわち近接作用論に回帰するような仮説立て、推察も行っていたのである。[6]
現代の初学者向けの科学史などでは、こうした複雑な経緯がすっかり忘れ去られ美化され、「ニュートンは原因の哲学的な思弁を避け、数的な関係の記述にとどめるという新しい方法論を提唱した」「力学の基礎、ひいては近代科学の考え方の基礎となった」とだけ解説がされていることもある。
万有引力の法則、その後[編集]
イギリス側の自然哲学者はニュートンの説を支持をする者が多かったが、その後、数十年以上の長い年数の議論を経て徐々に大陸側でも支持者が増え、やがては物理学においては自然界に存在する基本的な力だと見なされるようになっていった。
後の時代で発見された電磁気力では、引力と斥力がある、とされているのに対して、重力(万有引力)では引力しか存在せず、斥力は存在しない。
現在では、重力と呼ぶ場合には、質量に加速度を与える力全般を意味する。重力には、地球自転の遠心力のような慣性の力や、一般相対論で予言される慣性系の引きずりによる力も含まれるが、それらは万有引力ではない[要出典]。
重力(または重力相互作用)の正体は、アルベルト・アインシュタインの一般相対性理論では、質量を持つ物体が引き起こす時空の歪みである、と説明された。これに対して、'万有引力'という用語は、ニュートンの定式化した重力の意味で用いられる傾向にある。[要出典]
今日、質量を有する任意の2物体が引力の相互作用ポテンシャルを伴うことは、疑いのない自然法則として認められているが、その理由や機構についての研究は進んでいないという状況にあると言える。
一般相対性理論と重力[編集]
アインシュタインは、光速度に近い場合の力学として、1905年に特殊相対性理論を発表した後、加速度運動を含めた相対性理論の構築に取り掛かかった。そして重力場を時空の幾何学として取り扱う方法を模索し、1916年に一般相対性理論を発表した。
アインシュタインの重力場の方程式(アインシュタイン方程式)では、万有引力はもはやニュートン力学的な力ではなく、重力場という時空の歪みである、と説明されるようになった。また、重力の作用は、瞬時ではなく光速度で伝えられる、とされるようになった。
ニュートンの万有引力の法則では、質量を持った物体間の力であるとされるので、質量を持たない物質には万有引力は存在しない事となる。[要出典] 一般相対性理論では、重力が時空の歪みであるとするため、光の軌道もまた重力によって曲がる事を意味する。これはアーサー・エディントン による観測で実証されることになった。
一般相対性理論は、非常に強い重力が働く場を記述する。[要出典] 太陽系であれば、ニュートン力学に若干の補正項が加わる程度なので、ニュートン力学はその意味で近似的に正しいと考えて差し障りない。例えば前述の光の軌道の歪みについても、太陽の近傍においてようやく観測され得るものである。 アインシュタイン方程式は、通常の物理の方程式と同様、時間反転に対して対称なので、宇宙全体に適用すると、重力の影響で収縮宇宙の解と共に、膨張宇宙の解が得られる[要出典]、という。
一般相対性理論の発表当時は、ハッブルによる膨張宇宙の発見前で、アインシュタインは「宇宙は静的で安定している」と考えていた。自身の方程式が、動的な宇宙を予言したため、アインシュタインは万有引力に拮抗する万有斥力があると想定し、重力場の方程式に宇宙項を加えることで、静的な解が存在できるように重力場の方程式を修正した。
後に彼は宇宙項を「生涯最大の過ち」と悔いた。
「だが、宇宙項のアイデアは現在の宇宙論では、宇宙のインフレーションや宇宙の加速膨張を説明するものとして復活していると言える[要出典]」と言う。
「相対性理論」も参照
素粒子物理学と重力[編集]
素粒子物理学では、自然界に存在する四つの基本的な相互作用のひとつとして、素粒子間に働く重力相互作用とみなされ、重力子(グラヴィトン)という素粒子により媒介するとみなされるが、素粒子としての重力子は現在のところ未発見である。素粒子間の重力相互作用は無視できるほど小さいが、素粒子と地球との間の重力を考慮する必要があることもある。[要出典]
(※「ひとつの原子に存在する電子の数と陽子の数は同じで、種類によって数が決まっている。により、やはり電荷を帯びた電子が運動する事により電磁波が生まれ、それが引き付けあう力(反発力より若干大きい為)が発生し引力として認識される[要出典]、とする説もある。)
量子重力[編集]
近年では、量子力学と一般相対性理論の結合、重力の量子化が試みられ、量子重力と呼ばれている。格子重力などさまざまな試みがあるが、実現は困難である。量子重力を宇宙論に適用する試みは、量子宇宙論と呼ばれる。
出典[編集]https://ja.wikipedia.org/wiki/%E4%B8%87%E6%9C%89%E5%BC%95%E5%8A%9B
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 275: The division by zero $z/0=0$ and special relative theory of Einstein
}
\author{{\it Institute of Reproducing Kernels}\\
\date{January 11, 2016}
\maketitle
{\bf Abstract: } In this announcement, for its importance, we will state a fundamental result for special relative theory of Einstein from the division by zero $z/0=0$.
\bigskip
{\bf Introduction}
\bigskip
%\label{sect1}
By {\bf a natural extension of the fractions}
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, the division by zero
\begin{equation}
\frac{b}{0}=0,
\end{equation}
is clear and trivial. See (\cite{msy}) for the recent results. See also the survey style announcements 179,185,237,246,247,250 and 252 of the Institute of Reproducing Kernels (\cite{ann179,ann185,ann237,ann246,ann247,ann250,ann252}). The division by zero is not only mathematical problems, but also it will give great impacts to human beings and the idea on the universe. The Institute of Reproducing Kernels is presenting various opinions in Announcements (many in Japanese) on the universe.
In this Announcement, for its importance, we will state a fundamental result for special relative theory of Einstein from the division by zero $z/0=0$. The contents were stated by Hiroshi Michiwaki in his memo dated on October 10, 2014 and we should state the results, more early.
\section{Special relative theory of Einstein}
Einstein's discovery of the equivalence of matter/mass and energy \cite{ein} in the year 1905 lies
at the core of today's modern physics. According to Albert Einstein \cite{einstein}, the rest-mass $m_0$, a
measure of the inertia of a (quantum mechanical) object is related to the relativistic mass $m_R$
by the equation, with relative velocity $v$ and the speed $c$ of light in vacuum,
\begin{equation}
m_0 = m_R \sqrt{1 - \frac{v^2}{c^2}}.
\end{equation}
Therefore, we obtain, immediately
\begin{equation}
m_R^2= m_0^2 \left(1 - \frac{v^2}{c^2}\right)^{-1}.
\end{equation}
Therefore, by the division by zero, we have the surprising result for $ v = c$:
\begin{equation}
m_R = 0.
\end{equation} It seems that the modern physical common sense is then $
m_R = + \infty$.
\bigskip
\section{ A conjecture by H. Michiwaki}
As his simple result (1.3) from the division by zero, Michiwaki stated his conjecture or interpretation for neutrino; neutrino are able to have small mass, because they are moved with near $c$ or $c$ velocity.
Indeed, we assume that $m_0$ is the mass of neutrino at the stopped case. As the experiment, we know that the velocity of neutrino is near to $c$ or $c$. So he thought
that neutrino will have small mass.
This result was realized positively by Takaaki Kajita by experiment and he got Novel Prize in 2015.
Furthermore, he referred to the very interesting interpretations of {\it photon of energy} and {\it Doppler effect} from the viewpoint of the division by zero in his memo.
\section{Acknowledgements}
This announcement was, of course, inspired by the paper \cite{bb} and for the very interesting relation with computer sciences and the division by zero, see \cite{bht}.
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{bb}
Barukcic J. P., and I. Barukcic, Anti Aristotle - The Division Of Zero By Zero,
ViXra.org (Friday, June 5, 2015)
© Ilija Barukčić, Jever, Germany. All rights reserved. Friday, June 5, 2015 20:44:59.
\bibitem{bht}
Bergstra, J. A., Hirshfeld Y., and Tucker, J. V.,
Meadows and the equational specification of division (arXiv:0901.0823v1[math.RA] 7 Jan 2009).
\bibitem{cs}
Castro, L. P., and Saitoh, S. (2013).
Fractional functions and their representations. {\it Complex Anal. Oper. Theory {\bf7}, no. 4, }1049-1063.
\bibitem{ein}
Einstein, A. (1905) Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?, Annalen der Physik, vol. 323, Issue 13, pp. 639-641,
\bibitem{einstein}
Einstein, A. (1905).
Zur Elektrodynamik bewegter Körper, Annalen der Physik, vol. 322, Issue 10, pp. 891-921.
\bibitem{kmsy}
Kuroda, M., Michiwaki, H., Saitoh, S., and Yamane, M. (2014).
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
{\it Int. J. Appl. Math. Vol. 27, No 2 }, 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msy}
Michiwaki H., Saitoh S., and Yamada M. (2015).
Reality of the division by zero $z/0=0$. IJAPM (International J. of Applied Physics and Math. (to appear).
\bibitem{mst}
Michiwaki, H., Saitoh, S., and Takagi, M.
A new concept for the point at infinity and the division by zero z/0=0
(manuscript).
\bibitem{s}
Saitoh, S. (2014).
Generalized inversions of Hadamard and tensor products for matrices,
{\it Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 , 87-95.} http://www.scirp.org/journal/ALAMT/
\bibitem{taka}
Takahasi, S.-E. (2014).
{On the identities $100/0=0$ and $ 0/0=0$.}
(note)
\bibitem{ttk}
Takahasi, S.-E., Tsukada, M., and Kobayashi, Y. (2015).
{\it Classification of continuous fractional binary operations on the real and complex fields. } Tokyo Journal of Mathematics {\bf 8}, no.2(in press).
\bibitem{ann179}
Division by zero is clear as z/0=0 and it is fundamental in mathematics. {\it Announcement 179 (2014.8.30).}
\bibitem{ann185}
The importance of the division by zero $z/0=0$. {\it Announcement 185 (2014.10.22)}.
\bibitem{ann237}
A reality of the division by zero $z/0=0$ by geometrical optics. {\it Announcement 237 (2015.6.18)}.
\bibitem{ann246}
An interpretation of the division by zero $1/0=0$ by the gradients of lines. {\it Announcement 246 (2015.9.17)}.
\bibitem{ann247}
The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$. {\it Announcement 247 (2015.9.22)}.
\bibitem{ann250}
What are numbers? - the Yamada field containing the division by zero $z/0=0$. {\it Announcement 250 (2015.10.20)}.
\bibitem{ann252}
Circles and curvature - an interpretation by Mr. Hiroshi Michiwaki of the division by
zero $r/0 = 0$. {\it Announcement 252 (2015.11.1)}.
\end{thebibliography}
\end{document}
再生核研究所声明 264 (2015.12.23): 永遠とは何か ― 永遠から
現代人は 空間とは 座標軸で表される数の組の集合 で表させるものと発想しているだろう。 基礎である直線は 実数を直線上に並べたもの、逆に直線とは 実は 実数全体の表現と考えられる。 すなわち、直線とは 基準点である原点ゼロから、正方向と負方向に正の実数と負の実数が大小関係で順序づけられ無限に双方向に伸びていると考えられる。
そこで、永遠とは 直線に時間を対応させ、限りなく正方向に進んだ先のことを 想像している。どこまでも どこまでも 先に行けばどうなるだろうか。直線上でも、平面上でも である。 砂漠の伝統を有する欧米文化の背景、キリスト教などの背後には、 永遠とは限りなく 果てしなく先にあると発想しているという。 どこまでも、どこまでも きりのない世界である。 ユークリッド幾何学が そのような空間を考えていることは確かである。
ところが四季に恵まれたアジアの民は、限りなく広がる世界に、不安や淋しさを直感して、 正の先と、負の先が一致していて、直線は円で どこまでも どこまでも行くと反対方向から、現在に至り、永遠は繰り返しであると、四季の繰り返し、天空の繰り返し、円運動のように発想して 仄かな安心感を覚えているという。永劫回帰、輪廻の思想を深く懐いている。実に面白いことには 美しい複素解析学では、立体射影の考えによって、直線を球面上の円と表現し、無限遠点の導入によって、 これらの思想を 数学的に厳格に実現させ、全ユークリッド平面の全貌を捉え、無限の彼方さえ捉えることが出来た。 その時 永遠を 確かに捉え、掴むことさえ出来たと言える。立体射影による球面上の北極に 確かに存在すると言える。素晴しい、数学を手に入れていた。この美しい数学は 100年以上もリーマン球面として、複素解析学の基本となってきている。
ところが2014.2.2偶然に発見されたゼロ除算の結果は、この無限遠点が 実は原点に一致していた という衝撃的な事実を述べていた。 永遠、無限の彼方と想像していたら、それが 実は原点に戻っていたという事実である。 それが我々の数学であり、ユークリッド空間の実相である。幾何学の性質や物理的な法則をきちんと説明している、我々の世界の数学である。
それで、永遠や無限遠点、我々の空間の 十分先の考え方、発想を考える必要がある。
無限の先が原点に一致している事実、それを如何に理解すべきであろうか。
それについて、 次のように解説してきた:
再生核研究所声明232(2015.5.26)無限大とは何か、無限遠点とは何か。― 驚嘆すべきゼロ除算の結果
再生核研究所声明257 (2015.11.05) 無限大とは何か、 無限遠点とは何か ー 新しい視点
再生核研究所声明262 (2015.12.09) 宇宙回帰説 ― ゼロ除算の拓いた世界観
新しい世界観は 始まりから始まり 最後には 突然戻るということを述べている。 しからば、始めとは何で 終りとは何だろうか。 これについて、 始めも終わりも、質的な変化であると定義できるのではないだろうか。 簡単な数学で万物、universe の現象を説明するのは難しい状況は確かにあるだろう.しかし、ゼロ除算の思想は、新羅万象が絶えず変化して 繰り返している様を表現しているように感じられる。
大事な人生の視点は 今日は 明日のためや遠い未来のためにあるのではなく、 現在、現在における在るべき適切な在りようが大事だと言っているようである。もちろん、現在は、未来と過去に関係する存在であり、それらは関係付けられ、繋がっているが 焦点はもちろん、 現在にあるということである。
ビッグバンの宇宙論は 適切に理解され、始めとは 大きな変化で 現状の元が始まり、
やがて突然、元に戻って 終わることを暗示しているようである。人生とは 要するに 内なる自分と環境に調和するように在れ と ゼロ除算は言っているようである。
ゼロ除算は 仏教の偉大なる思想 を暗示させているように感じられる。
以 上
Reality of the Division by Zero z/0 = 0
http://www.ijapm.org/show-63-504-1.html
http://okmr.yamatoblog.net/
再生核研究所声明262 (2015.12.09) 宇宙回帰説 ― ゼロ除算の拓いた世界観
最近展開しているゼロ除算が、新しい世界観を示しているのは 大変興味深い。直線とは一体どうなっているだろうか.空間とはどのようになっているだろうか。これについて、現代人は、双方向にどこまでも どこまでも 続いている直線を想像するであろう。限りなく広がった平面や空間である。ところが 立体射影によって 平面全体を球面上に1対1に写せば、全平面は 球面から北極を除いた球面上に1対1にきちんと写るから、無限に広がる 全平面の全貌が捉えられる。ところが平面上には存在しない想像上の点 それはあらゆる方向に限りなく遠くに存在する無限遠点の導入によって、その点を球面の欠けた1点北極に対応させれば、無限遠点を含めた平面全体は 球面全体と1対1にきちんと対応する。
このような対応で 平面上の円や直線全体は 球面上では共に円に対応するという美しい対応になり、平面上の直線は 球面上では、北極(無限遠点)を通る円に写ると、直線と円の区別は 球面上では不要になる。また、平面上の平行線とは 無限遠点で 角度ゼロで交わっている(接している)と平面上の構造がよく見えて、無限遠点を含めての平面の全構造が 捉えられる。このように、考えると、直線とは、球面上では北極を通る円、平面上では無限遠点を通る直線となる。この構造は、直線を1方向にどこまでも, どこまでも進めば、無限遠点を 通って、逆方向から戻ってくるという、永劫回帰の思想をちょうど実現している。それは、球面上では、 円を繰り返し回ることを意味する。 その様は 何もかも すっかり良く見える。
これが、従来100年以上も続いた世界観で、関数y=x やW=zは 無限遠点に近づけば、それらの像も無限遠点に近づいていると考えるだろう。 関数y=x の値は正方向にどんどん行けば、どんどん大きくなると考えるだろう。
しかるに、ゼロ除算1/0=0は、それらの関数は無限遠点にいくらでも近づくと 無限遠点にいくらでも近づくが、無限遠点自身では、突然ゼロになっていることが 幾何学的にも確認された。上記、北極は 実は原点ゼロに一致しているという。
話しを簡単にするために、 関数y=x を考えよう。右に行けば、プラス無限に、負の方向左に行けば 負の無限に限りなく近づくは 従来通りである。ところが、ゼロ除算では いずれの方向でも上記無限遠点では 値ゼロをきちんと取っているという。ゼロ除算の数学では、どんどん、増加した先、突然、ゼロ、原点に戻っているという。また、円でも球面でも半径Rをどんどん大きくすると、当然、円の面積や球の体積はどんどん限りなく大きくなるが、半径が無限のとき、突然、それらはゼロになるという。それらの理由も数学ばかりではなく、幾何学的にも明確に見えている。
この数学的な事実は、我々の世界、宇宙がどんどん拡大して行くと突然、ゼロに帰するということを暗示させている。 ― これは 宇宙回帰説を意味しているようである。
これは、ユニバースの普遍的な現象、どんどん進んだ先が、元に突然戻る原理を示しているようである。
そもそも人生とは如何なるものか。― よくは分からないが、事実として、生まれて、どんどん物心がついて、人間として精神活動が活発化して、多くは本能原理によって生かされて、そして、突然元に戻ることを意味しているようである。このことを深く捉えられれば、世界がよりよく観え、悟りの境地に達する大きなヒントを得ることができるだろう。
ここでは ゼロ除算の帰結として、宇宙回帰説、ユニバースの回帰説を唱えたい。この考えでは、どんどん進めば、突然元に戻るという原理を述べている。珠算における 御破算で願いましては で 再び始めることを想起させる。これは、また、reset と同様であると考えられる。
以 上
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
https://notevenpast.org/dividing-nothing/
割り算のできる人には、どんなことも難しくない
世の中には多くのむずかしいものがあるが、加減乗除の四則演算ほどむずかしいものはほかにない。
ベーダ・ヴェネラビリス
数学名言集:ヴィルチェンコ編:松野武 山崎昇 訳大竹出版1989年
Reality of the Division by Zero z/0 = 0
http://www.ijapm.org/show-63-504-1.html
http://okmr.yamatoblog.net/










0 件のコメント:
コメントを投稿