1나누기 0은?…“풀어보세요”
온라인이슈팀 기자
입력 : 2013.11.10.10:03
수정 : 2013.11.10.10:03
2 페이스북트위터구글
‘1나누기 0은?’에 대한 누리꾼들의 호기심이 일고 있다.
최근 주요 온라인 커뮤니티 게시판에는 1나누기 0이 가능한 공식 인지에 대한 글이 올라왔다. 가능성 여부를 두고 누리꾼들의 설전이 오간 것.
1나누기 0은?이란 제목의 글에는 1나누기 0이 수학적으로 가능한 계산인지에 대한 내용과 성립하지 않는다는 증명 영상이 담겨 있어 눈길을 끈다.
이 설명에 따르면 1나누기 0을 증명하는 방법은 간단하다. 나눗셈의 역연산인 곱셈을 생각하면 되기 때문이다.
1
A÷B를 계산한 답이 C가 나온다는 것은 반대로 C와 B를 곱하면 A가 나오는 답이 성립해야 한다. 예를 들어 2를 0으로 나누는 것이 가능해 그 답을 C라고 한다면 C*0=2가 된다는 말과 마찬가지기 때문에 성립할 수 없게 되는 것이다.
1나누기 0은? 풀이를 본 누리꾼들은 “1나누기 0 계산이 성립 불가한 이유를 이제 좀 알겠다”, “1을 0으로 나눈다고 뭐가 달라질까”, “수학의 세계는 역시 신기하다” 등의 반응을 보였다.
→ 한 뼘 더 깊은 IT 보고서 ‘리소스 라이브러리’ 에서 만나보세요!
관련기사
삼천포 이름 공개, “깨알 재미가…”
‘응답하라 1994’가 큰 인기를 끄는 가운데 극중 캐릭터인 ‘삼천포’의 이름이 알려져 화제다. 지난 9일 ...
GTA 군대, 이등병 선택한 김민교 운명은?
지붕 뚫린 비행기, “승객들 어떡하라고”
슈퍼스타K5, 송희진 탈락…결승 진출자는?
수영 시험 마친 호랑이, 누리꾼 “귀엽네”
온라인이슈팀 기자 (issue@zdnet.co.kr) 기자의 다른 기사 보기
저작권자 © ZDNet Korea 무단전재-재배포 금지
TAGS
1나누기0은온라인누리꾼수학
AD [단독] 스마트폰&PC완벽 호환…가장 얇고 가벼운 블루투스 키보드 출시
AD
AD
AD
AD
주요뉴스
투자 심리 위축 속 中 스타트업 통합 확산
야후, 인터넷 사업 매각 검토
네이버, 아마추어 웹툰 창작자에 장학금 지원
"연말정산 정보는 네이버 지식인에서"
파이어폭스, 지원 끊겠다던 SHA1 임시 허용...왜?
인포그래픽 뉴스
패블릿 전성시대…"네 대 중 한대가 대형폰"
인터뷰
웹표준 제대로 쓰게 하는 솔루션 수요 확산
"애플 3D터치?"...토종 벤처, 먼저 내놨다
소셜로그인Kakao 로그인 페이지 새창이 열립니다Naver 로그인 페이지 새창이 열립니다Facebook 로그인 페이지 새창이 열립니다Twitter 로그인 페이지 새창이 열립니다GooglePlus 로그인 페이지 새창이 열립니다LinkedIn 로그인 페이지 새창이 열립니다
로그인 전 프로필 이미지
욕설과 타인에 대한 근거없는 비방에 따른 명예훼손 우려가 있는 글은 관리자에 의해 삭제됩니다.
로그인 후 입력하세요
스티커 사용하기 버튼스티커 사용하기 버튼 0/250 입력
Powered by LiveRe
주요뉴스
AR폰 구글 '프로젝트 탱고' 베일 벗다
구글이 진행해 온 3D 증강현실(AR) 솔루션 개발 '프로젝트 탱고'의 첫 번째 결과물이 베일을 벗었다.레노버와 구글은 7일(현지시간) 세계 최대 가전박람회 CES 2016이 열리는 미국 라스베이거스에서 특별 행사를 ...
스마트폰시장 한파…삼성-애플 '우울'
"넷플릭스가 들어 와야 정신차리지"
CES에 휘몰아친 '차이나 광풍(狂風)'
테슬라 “한국 시장서 곧 차량 판매 시작”
준대형세단 大戰...기세 올리는 신흥강자는?
기어S2, 마시멜로 G4와 호환 문제 일으켜
이슈칼럼게임뉴스
추천 AD
123http://www.zdnet.co.kr/news/news_view.asp?artice_id=20131110100309
Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics\\
}
\author{{\it Institute of Reproducing Kernels}\\
\date{\today}
\maketitle
{\bf Abstract: } In this announcement, we shall introduce the zero division $z/0=0$. The result is a definite one and it is fundamental in mathematics.
\bigskip
\section{Introduction}
%\label{sect1}
By a natural extension of the fractions
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, we, recently, found the surprising result, for any complex number $b$
\begin{equation}
\frac{b}{0}=0,
\end{equation}
incidentally in \cite{s} by the Tikhonov regularization for the Hadamard product inversions for matrices, and we discussed their properties and gave several physical interpretations on the general fractions in \cite{kmsy} for the case of real numbers. The result is a very special case for general fractional functions in \cite{cs}.
The division by zero has a long and mysterious story over the world (see, for example, google site with division by zero) with its physical viewpoints since the document of zero in India on AD 628, however,
Sin-Ei, Takahasi (\cite{taka}) (see also \cite{kmsy}) established a simple and decisive interpretation (1.2) by analyzing some full extensions of fractions and by showing the complete characterization for the property (1.2). His result will show that our mathematics says that the result (1.2) should be accepted as a natural one:
\bigskip
{\bf Proposition. }{\it Let F be a function from ${\bf C }\times {\bf C }$ to ${\bf C }$ such that
$$
F (b, a)F (c, d)= F (bc, ad)
$$
for all
$$
a, b, c, d \in {\bf C }
$$
and
$$
F (b, a) = \frac {b}{a }, \quad a, b \in {\bf C }, a \ne 0.
$$
Then, we obtain, for any $b \in {\bf C } $
$$
F (b, 0) = 0.
$$
}
\medskip
\section{What are the fractions $ b/a$?}
For many mathematicians, the division $b/a$ will be considered as the inverse of product;
that is, the fraction
\begin{equation}
\frac{b}{a}
\end{equation}
is defined as the solution of the equation
\begin{equation}
a\cdot x= b.
\end{equation}
The idea and the equation (2.2) show that the division by zero is impossible, with a strong conclusion. Meanwhile, the problem has been a long and old question:
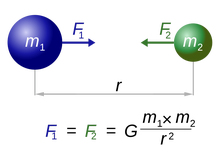
As a typical example of the division by zero, we shall recall the fundamental law by Newton:
\begin{equation}
F = G \frac{m_1 m_2}{r^2}
\end{equation}
for two masses $m_1, m_2$ with a distance $r$ and for a constant $G$. Of course,
\begin{equation}
\lim_{r \to +0} F =\infty,
\end{equation}
however, in our fraction
\begin{equation}
F = G \frac{m_1 m_2}{0} = 0.
\end{equation}
\medskip
Now, we shall introduce an another approach. The division $b/a$ may be defined {\bf independently of the product}. Indeed, in Japan, the division $b/a$ ; $b$ {\bf raru} $a$ ({\bf jozan}) is defined as how many $a$ exists in $b$, this idea comes from subtraction $a$ repeatedly. (Meanwhile, product comes from addition).
In Japanese language for "division", there exists such a concept independently of product.
H. Michiwaki and his 6 years old girl said for the result $ 100/0=0$ that the result is clear, from the meaning of the fractions independently the concept of product and they said:
$100/0=0$ does not mean that $100= 0 \times 0$. Meanwhile, many mathematicians had a confusion for the result.
Her understanding is reasonable and may be acceptable:
$100/2=50 \quad$ will mean that we divide 100 by 2, then each will have 50.
$100/10=10 \quad$ will mean that we divide 100 by10, then each will have 10.
$100/0=0 \quad$ will mean that we do not divide 100, and then nobody will have at all and so 0.
Furthermore, she said then the rest is 100; that is, mathematically;
$$
100 = 0\cdot 0 + 100.
$$
Now, all the mathematicians may accept the division by zero $100/0=0$ with natural feelings as a trivial one?
\medskip
For simplicity, we shall consider the numbers on non-negative real numbers. We wish to define the division (or fraction) $b/a$ following the usual procedure for its calculation, however, we have to take care for the division by zero:
The first principle, for example, for $100/2 $ we shall consider it as follows:
$$
100-2-2-2-,...,-2.
$$
How may times can we subtract $2$? At this case, it is 50 times and so, the fraction is $50$.
The second case, for example, for $3/2$ we shall consider it as follows:
$$
3 - 2 = 1
$$
and the rest (remainder) is $1$, and for the rest $1$, we multiple $10$,
then we consider similarly as follows:
$$
10-2-2-2-2-2=0.
$$
Therefore $10/2=5$ and so we define as follows:
$$
\frac{3}{2} =1 + 0.5 = 1.5.
$$
By these procedures, for $a \ne 0$ we can define the fraction $b/a$, usually. Here we do not need the concept of product. Except the zero division, all the results for fractions are valid and accepted.
Now, we shall consider the zero division, for example, $100/0$. Since
$$
100 - 0 = 100,
$$
that is, by the subtraction $100 - 0$, 100 does not decrease, so we can not say we subtract any from $100$. Therefore, the subtract number should be understood as zero; that is,
$$
\frac{100}{0} = 0.
$$
We can understand this: the division by $0$ means that it does not divide $100$ and so, the result is $0$.
Similarly, we can see that
$$
\frac{0}{0} =0.
$$
As a conclusion, we should define the zero divison as, for any $b$
$$
\frac{b}{0} =0.
$$
See \cite{kmsy} for the details.
\medskip
\section{In complex analysis}
We thus should consider, for any complex number $b$, as (1.2);
that is, for the mapping
\begin{equation}
w = \frac{1}{z},
\end{equation}
the image of $z=0$ is $w=0$. This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere.
However, we shall recall the elementary function
\begin{equation}
W(z) = \exp \frac{1}{z}
\end{equation}
$$
= 1 + \frac{1}{1! z} + \frac{1}{2! z^2} + \frac{1}{3! z^3} + \cdot \cdot \cdot .
$$
The function has an essential singularity around the origin. When we consider (1.2), meanwhile, surprisingly enough, we have:
\begin{equation}
W(0) = 1.
\end{equation}
{\bf The point at infinity is not a number} and so we will not be able to consider the function (3.2) at the zero point $z = 0$, meanwhile, we can consider the value $1$ as in (3.3) at the zero point $z = 0$. How do we consider these situations?
In the famous standard textbook on Complex Analysis, L. V. Ahlfors (\cite{ahlfors}) introduced the point at infinity as a number and the Riemann sphere model as well known, however, our interpretation will be suitable as a number. We will not be able to accept the point at infinity as a number.
As a typical result, we can derive the surprising result: {\it At an isolated singular point of an analytic function, it takes a definite value }{\bf with a natural meaning.} As the important applications for this result, the extension formula of functions with analytic parameters may be obtained and singular integrals may be interpretated with the division by zero, naturally (\cite{msty}).
\bigskip
\section{Conclusion}
The division by zero $b/0=0$ is possible and the result is naturally determined, uniquely.
The result does not contradict with the present mathematics - however, in complex analysis, we need only to change a little presentation for the pole; not essentially, because we did not consider the division by zero, essentially.
The common understanding that the division by zero is impossible should be changed with many text books and mathematical science books. The definition of the fractions may be introduced by {\it the method of Michiwaki} in the elementary school, even.
Should we teach the beautiful fact, widely?:
For the elementary graph of the fundamental function
$$
y = f(x) = \frac{1}{x},
$$
$$
f(0) = 0.
$$
The result is applicable widely and will give a new understanding for the universe ({\bf Announcement 166}).
\medskip
If the division by zero $b/0=0$ is not introduced, then it seems that mathematics is incomplete in a sense, and by the intoduction of the division by zero, mathematics will become complete in a sense and perfectly beautiful.
\bigskip
section{Remarks}
For the procedure of the developing of the division by zero and for some general ideas on the division by zero, we presented the following announcements in Japanese:
\medskip
{\bf Announcement 148} (2014.2.12): $100/0=0, 0/0=0$ -- by a natural extension of fractions -- A wish of the God
\medskip
{\bf Announcement 154} (2014.4.22): A new world: division by zero, a curious world, a new idea
\medskip
{\bf Announcement 157} (2014.5.8): We wish to know the idea of the God for the division by zero; why the infinity and zero point are coincident?
\medskip
{\bf Announcement 161} (2014.5.30): Learning from the division by zero, sprits of mathematics and of looking for the truth
\medskip
{\bf Announcement 163} (2014.6.17): The division by zero, an extremely pleasant mathematics - shall we look for the pleasant division by zero: a proposal for a fun club looking for the division by zero.
\medskip
{\bf Announcement 166} (2014.6.29): New general ideas for the universe from the viewpoint of the division by zero
\medskip
{\bf Announcement 171} (2014.7.30): The meanings of product and division -- The division by zero is trivial from the own sense of the division independently of the concept of product
\medskip
{\bf Announcement 176} (2014.8.9): Should be changed the education of the division by zero
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{ahlfors}
L. V. Ahlfors, Complex Analysis, McGraw-Hill Book Company, 1966.
\bibitem{cs}
L. P. Castro and S.Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
S. Koshiba, H. Michiwaki, S. Saitoh and M. Yamane,
An interpretation of the division by zero z/0=0 without the concept of product
(note).
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msty}
H. Michiwaki, S. Saitoh, M. Takagi and M. Yamada,
A new concept for the point at infinity and the division by zero z/0=0
(note).
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95. http://www.scirp.org/journal/ALAMT/
\bibitem{taka}
S.-E. Takahasi,
{On the identities $100/0=0$ and $ 0/0=0$}
(note).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operators on the real and complex fields. (submitted)
\end{thebibliography}
\end{document}
アインシュタインも解決できなかった「ゼロで割る」問題
http://matome.naver.jp/odai/2135710882669605901
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
https://notevenpast.org/dividing-nothing/
私は数学を信じない。 アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。
1423793753.460.341866474681。









0 件のコメント:
コメントを投稿