関連研究者
相馬清吾
相馬清吾 科学研究費助成事業
東北大学・准教授 - 2014年度(平成26年度)
研究分野 物理学
キーワード 角度分解光電子分光 スピントロニクス 新機能物質 トポロジカル絶縁体 界面
高橋隆
高橋隆 チーム型研究 科学研究費助成事業
東北大学・教授 - 2015年度(平成27年度)
研究分野 物理学 ナノテクノロジー・材料・光技術
キーワード 酸化物高温超伝導体 新機能物質 逆光電子分光 電子構造 高分解能光電子分光
佐藤宇史
佐藤宇史 新規材料による高温超伝導基盤技術 科学研究費助成事業
東北大学・理学(系)研究科(研究院)・准教授 - 2015年度(平成27年度)
研究分野 物理学
キーワード トポロジカル絶縁体 角度分解光電子分光法 フェルミ面 ディラックコーン 新機能物質
【概要】
東北大学原子分子材料科学高等研究機構の相馬清吾准教授、高橋隆教授、同理学研究科の佐藤宇史准教授らの研究グループは、ありふれた金属である鉄とタングステンを接合することによって、その界面に相対論的電子(ディラック電子)を発生させ、さらにディラック電子に巨大な質量を与えることに成功しました。今回の成果により、新機能を持つ次世代スピントロニクスデバイスの開発が大きく進展するものと期待されます。本成果は、平成 27 年 12 月 23 日(米国東部時間)に米国物理学会誌フィジカル・レビュー・レターズのオンライン速報版に掲載されました。
【研究の背景】
電子は普通の物質の中では、有限の質量をもった粒子として物質内を動き回ります。ところが最近、物質中においてあたかも質量がゼロの粒子のように振る舞う「ディラック電子」注 1)と呼ばれる特殊な電子が発見され、大きな注目を集めています。そのような電子は、真空中で光速に近い速度で運動する粒子(例えば、素粒子ニュートリノ)と同じような性質を示すことから、物質中の相対論的電子と呼ばれています。次世代電子デバイス材料として大きな注目を集めているグラフェンやトポロジカル絶縁体注 2)は、相対論的なディラック電子を持つ物質として知られています。ディラック電子は、物質中でディラック錐(図 1)と呼ばれる電子の状態を形成しています。ディラック電子は物質中の普通の電子よりも格段に動きやすい上に、不純物に邪魔されにくいという性質を持ち、さらに電流などによってスピン注 3)の向きも制御できます。その優れた性質を利用して、次世代デバイス実現へ向けた研究が、現在世界中で急ピッチに進められています。
これまで、グラフェンやトポロジカル絶縁体デバイスの多くでその機能を利用するには、このディラック電子に意図的に質量を持たせてその運動を制御する(図 1)事が重要とされてきました。またこれが実現されると、グラフェンの半導体デバイスへの応用、トポロジカル絶縁体における分数量子ホール効果注 4)や磁気単極子注 5)などといった様々な応用・特異量子現象が実現される可能性も指摘されています。しかしながら現段階では、ディラック電子は極めて限られた物質でしか観測されておらず、その制御も困難なため、新しいディラック電子系の探索とその質量制御が急務とされてきました。
【研究の内容】
今回、東北大学の研究グループは、分子エピタキシー法注 6)によって、タングステンの表面にわずか数原子層の鉄超薄膜を成長し、外部光電効果注 7)を利用した角度分解光電子分光注 8)という手法を用いて、鉄とタングステンの界面から電子を直接引き出して(図 2)、そのエネルギー状態を高精度で調べました。実験の結果、鉄超薄膜を接合する前は質量がゼロだった結晶表面のディラック電子が、鉄超薄膜を接合することによって質量を獲得している(図 3)ことを初めて明らかにしました。また、その質量の大きさは、トポロジカル絶縁体にくらべて遥かに(数倍程度)大きいことがわかりました。さらに、鉄超薄膜の磁化の向き(表面に垂直または平行)を制御することで、質量獲得の有無の切り替えができることを発見しました (図 4)。この成果は、ディラック電子を利用した室温動作次世代スピントロニクスデバイス開発に大きく貢献するものです。
【今後の展望】
今回の研究は、ディラック物質に強磁性体を接合するという比較的簡便な方法で、従来よりも遥かに大きい質量をディラック電子に付与できることを実験的に示したものです。これによって、ディラック電子の状態を自由自在に制御できる新しい方法が示されました。この成果を、新物質の設計や電子スピン状態の制御に利用することで、新しいディラック電子系物質の開発が進み、次世代の省エネ技術である革新的なスピントロニクス注 9)デバイスや、超高速処理を行う量子コンピュータ注 10)の実現の可能性がさらに進むと期待されます。
本成果は、科研費基盤研究(A)「スピン分解 ARPES による機能性薄膜ハイブリッドの創出」(研究代表者: 高橋 隆)、新学術領域「トポロジーが紡ぐ物質科学のフロンティア」(領域代表者: 川上則雄)および「原子層科学」(領域代表者: 齋藤理一郎)、学際研究重点プログラム「原子層超薄膜における革新的電子機能物性の創発」(研究代表者: 高橋 隆)などの援助によって得られました。【論文情報】
Kohei Honma, Takafumi Sato, Seigo Souma, Katsuaki Sugawara, Yusuke Tanaka,and Takashi Takahashi, “Switching of Dirac-Fermion Mass at the Interface of Ultrathin Ferromagnet and Rashba Metal”, Physical Review Letters, DOI : http://dx.doi.org/10.1103/PhysRevLett.115.266401.
https://research-er.jp/articles/view/41965
Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics\\
}
\author{{\it Institute of Reproducing Kernels}\\
\date{\today}
\maketitle
{\bf Abstract: } In this announcement, we shall introduce the zero division $z/0=0$. The result is a definite one and it is fundamental in mathematics.
\bigskip
\section{Introduction}
%\label{sect1}
By a natural extension of the fractions
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, we, recently, found the surprising result, for any complex number $b$
\begin{equation}
\frac{b}{0}=0,
\end{equation}
incidentally in \cite{s} by the Tikhonov regularization for the Hadamard product inversions for matrices, and we discussed their properties and gave several physical interpretations on the general fractions in \cite{kmsy} for the case of real numbers. The result is a very special case for general fractional functions in \cite{cs}.
The division by zero has a long and mysterious story over the world (see, for example, google site with division by zero) with its physical viewpoints since the document of zero in India on AD 628, however,
Sin-Ei, Takahasi (\cite{taka}) (see also \cite{kmsy}) established a simple and decisive interpretation (1.2) by analyzing some full extensions of fractions and by showing the complete characterization for the property (1.2). His result will show that our mathematics says that the result (1.2) should be accepted as a natural one:
\bigskip
{\bf Proposition. }{\it Let F be a function from ${\bf C }\times {\bf C }$ to ${\bf C }$ such that
$$
F (b, a)F (c, d)= F (bc, ad)
$$
for all
$$
a, b, c, d \in {\bf C }
$$
and
$$
F (b, a) = \frac {b}{a }, \quad a, b \in {\bf C }, a \ne 0.
$$
Then, we obtain, for any $b \in {\bf C } $
$$
F (b, 0) = 0.
$$
}
\medskip
\section{What are the fractions $ b/a$?}
For many mathematicians, the division $b/a$ will be considered as the inverse of product;
that is, the fraction
\begin{equation}
\frac{b}{a}
\end{equation}
is defined as the solution of the equation
\begin{equation}
a\cdot x= b.
\end{equation}
The idea and the equation (2.2) show that the division by zero is impossible, with a strong conclusion. Meanwhile, the problem has been a long and old question:
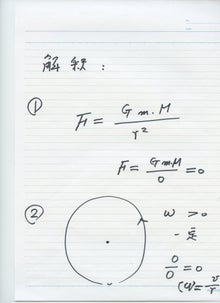
As a typical example of the division by zero, we shall recall the fundamental law by Newton:
\begin{equation}
F = G \frac{m_1 m_2}{r^2}
\end{equation}
for two masses $m_1, m_2$ with a distance $r$ and for a constant $G$. Of course,
\begin{equation}
\lim_{r \to +0} F =\infty,
\end{equation}
however, in our fraction
\begin{equation}
F = G \frac{m_1 m_2}{0} = 0.
\end{equation}
\medskip
Now, we shall introduce an another approach. The division $b/a$ may be defined {\bf independently of the product}. Indeed, in Japan, the division $b/a$ ; $b$ {\bf raru} $a$ ({\bf jozan}) is defined as how many $a$ exists in $b$, this idea comes from subtraction $a$ repeatedly. (Meanwhile, product comes from addition).
In Japanese language for "division", there exists such a concept independently of product.
H. Michiwaki and his 6 years old girl said for the result $ 100/0=0$ that the result is clear, from the meaning of the fractions independently the concept of product and they said:
$100/0=0$ does not mean that $100= 0 \times 0$. Meanwhile, many mathematicians had a confusion for the result.
Her understanding is reasonable and may be acceptable:
$100/2=50 \quad$ will mean that we divide 100 by 2, then each will have 50.
$100/10=10 \quad$ will mean that we divide 100 by10, then each will have 10.
$100/0=0 \quad$ will mean that we do not divide 100, and then nobody will have at all and so 0.
Furthermore, she said then the rest is 100; that is, mathematically;
$$
100 = 0\cdot 0 + 100.
$$
Now, all the mathematicians may accept the division by zero $100/0=0$ with natural feelings as a trivial one?
\medskip
For simplicity, we shall consider the numbers on non-negative real numbers. We wish to define the division (or fraction) $b/a$ following the usual procedure for its calculation, however, we have to take care for the division by zero:
The first principle, for example, for $100/2 $ we shall consider it as follows:
$$
100-2-2-2-,...,-2.
$$
How may times can we subtract $2$? At this case, it is 50 times and so, the fraction is $50$.
The second case, for example, for $3/2$ we shall consider it as follows:
$$
3 - 2 = 1
$$
and the rest (remainder) is $1$, and for the rest $1$, we multiple $10$,
then we consider similarly as follows:
$$
10-2-2-2-2-2=0.
$$
Therefore $10/2=5$ and so we define as follows:
$$
\frac{3}{2} =1 + 0.5 = 1.5.
$$
By these procedures, for $a \ne 0$ we can define the fraction $b/a$, usually. Here we do not need the concept of product. Except the zero division, all the results for fractions are valid and accepted.
Now, we shall consider the zero division, for example, $100/0$. Since
$$
100 - 0 = 100,
$$
that is, by the subtraction $100 - 0$, 100 does not decrease, so we can not say we subtract any from $100$. Therefore, the subtract number should be understood as zero; that is,
$$
\frac{100}{0} = 0.
$$
We can understand this: the division by $0$ means that it does not divide $100$ and so, the result is $0$.
Similarly, we can see that
$$
\frac{0}{0} =0.
$$
As a conclusion, we should define the zero divison as, for any $b$
$$
\frac{b}{0} =0.
$$
See \cite{kmsy} for the details.
\medskip
\section{In complex analysis}
We thus should consider, for any complex number $b$, as (1.2);
that is, for the mapping
\begin{equation}
w = \frac{1}{z},
\end{equation}
the image of $z=0$ is $w=0$. This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere.
However, we shall recall the elementary function
\begin{equation}
W(z) = \exp \frac{1}{z}
\end{equation}
$$
= 1 + \frac{1}{1! z} + \frac{1}{2! z^2} + \frac{1}{3! z^3} + \cdot \cdot \cdot .
$$
The function has an essential singularity around the origin. When we consider (1.2), meanwhile, surprisingly enough, we have:
\begin{equation}
W(0) = 1.
\end{equation}
{\bf The point at infinity is not a number} and so we will not be able to consider the function (3.2) at the zero point $z = 0$, meanwhile, we can consider the value $1$ as in (3.3) at the zero point $z = 0$. How do we consider these situations?
In the famous standard textbook on Complex Analysis, L. V. Ahlfors (\cite{ahlfors}) introduced the point at infinity as a number and the Riemann sphere model as well known, however, our interpretation will be suitable as a number. We will not be able to accept the point at infinity as a number.
As a typical result, we can derive the surprising result: {\it At an isolated singular point of an analytic function, it takes a definite value }{\bf with a natural meaning.} As the important applications for this result, the extension formula of functions with analytic parameters may be obtained and singular integrals may be interpretated with the division by zero, naturally (\cite{msty}).
\bigskip
\section{Conclusion}
The division by zero $b/0=0$ is possible and the result is naturally determined, uniquely.
The result does not contradict with the present mathematics - however, in complex analysis, we need only to change a little presentation for the pole; not essentially, because we did not consider the division by zero, essentially.
The common understanding that the division by zero is impossible should be changed with many text books and mathematical science books. The definition of the fractions may be introduced by {\it the method of Michiwaki} in the elementary school, even.
Should we teach the beautiful fact, widely?:
For the elementary graph of the fundamental function
$$
y = f(x) = \frac{1}{x},
$$
$$
f(0) = 0.
$$
The result is applicable widely and will give a new understanding for the universe ({\bf Announcement 166}).
\medskip
If the division by zero $b/0=0$ is not introduced, then it seems that mathematics is incomplete in a sense, and by the intoduction of the division by zero, mathematics will become complete in a sense and perfectly beautiful.
\bigskip
section{Remarks}
For the procedure of the developing of the division by zero and for some general ideas on the division by zero, we presented the following announcements in Japanese:
\medskip
{\bf Announcement 148} (2014.2.12): $100/0=0, 0/0=0$ -- by a natural extension of fractions -- A wish of the God
\medskip
{\bf Announcement 154} (2014.4.22): A new world: division by zero, a curious world, a new idea
\medskip
{\bf Announcement 157} (2014.5.8): We wish to know the idea of the God for the division by zero; why the infinity and zero point are coincident?
\medskip
{\bf Announcement 161} (2014.5.30): Learning from the division by zero, sprits of mathematics and of looking for the truth
\medskip
{\bf Announcement 163} (2014.6.17): The division by zero, an extremely pleasant mathematics - shall we look for the pleasant division by zero: a proposal for a fun club looking for the division by zero.
\medskip
{\bf Announcement 166} (2014.6.29): New general ideas for the universe from the viewpoint of the division by zero
\medskip
{\bf Announcement 171} (2014.7.30): The meanings of product and division -- The division by zero is trivial from the own sense of the division independently of the concept of product
\medskip
{\bf Announcement 176} (2014.8.9): Should be changed the education of the division by zero
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{ahlfors}
L. V. Ahlfors, Complex Analysis, McGraw-Hill Book Company, 1966.
\bibitem{cs}
L. P. Castro and S.Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
S. Koshiba, H. Michiwaki, S. Saitoh and M. Yamane,
An interpretation of the division by zero z/0=0 without the concept of product
(note).
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msty}
H. Michiwaki, S. Saitoh, M. Takagi and M. Yamada,
A new concept for the point at infinity and the division by zero z/0=0
(note).
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95. http://www.scirp.org/journal/ALAMT/
\bibitem{taka}
S.-E. Takahasi,
{On the identities $100/0=0$ and $ 0/0=0$}
(note).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operators on the real and complex fields. (submitted)
\end{thebibliography}
\end{document}
アインシュタインも解決できなかった「ゼロで割る」問題
http://matome.naver.jp/odai/2135710882669605901
Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.
https://notevenpast.org/dividing-nothing/
私は数学を信じない。 アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。









0 件のコメント:
コメントを投稿