21世紀は、ハングル時代、韓流文化の時代
2015年05月03日(日)NEW!
テーマ:数学
▲キム·ジョンテク(ハングル学会会長)
(前略:文明における文字の重要性)
今、私たち韓国人は韓国語で話して聞き、ハングルで書かれた文を読んで書くことができる。あま
りに当然の事実のようだがこれほど驚くべき事実はない。世の中で自国語と文が自然に分かり自
然に書いて読むことができる国民は私たちしかいないからです。
こうなったのは光復後、ハングルが国字の役割を果たしてからで、それほど昔のことではない。こ
の様なハングルの力、教育の力が土台になって今日、漢江(ハンガン)の奇跡という経済的・文化
的成就を成し遂げることができたのです。
視線を転じて考えてみよう。私たちにはただで与えられたような国語能力を得るために中国人は
一生を捧げて努力している。漢字は難しいと簡体字を作って使っているが、正しい表音文字では
ないのである程度の数の語彙を習わなければならない。初等学校で二千五百字を学び中学校で
さらに千字を習っても新聞はコラム周辺の案内表示板さえまともに読むことはできない。教養人と
して生きるなら最低五千字は習わなければならず大変だ。反復学習しなければ忘れるので、彼ら
は一生、字の勉強をしながら生きなければならない。
日本も同じだ。永い歳月をかけた時代ごと地域ごとに勝手に定着した無秩序な漢字借用表記が
日常化されたので同じ漢字でもその時や地方によって音が違い、意味が違い、いちいちカナで音
を付けなければ読むこともできず意味を知ることもできない。'日本'と書いて、ある時は'ニッポン'と
読み、ある時は'ニホン'と読まねばならず、また、'海老'と書いて全く関係ない音'エビ'と発音し全く
関係ない意味'セウ'(訳注:韓国語でエビのこと)を習わなければならないが、それでどうして正常
な漢字の使い道といえるだろうか。
私たちの子供たちが'ありがとうございます。'と言う時、日本の子供たちは'有難'と書いて'ありがと
う'と読む方法を習わなければならず、それは容易ではない。やはり中学校、高校を出ても読んで
書く国語生活を自然にはできない。
(中略:シンガポール、フィリピン、インド、米国の事例及びハングルの優秀性)
世界で最も優秀な表音文字であるハングルは私たちの韓流文化とともに必ず世界へ広がるだろ
う。古代ギリシャ文字が最小の表音文字で古代西洋文化を導いたように、中世ローマ字が千年の
ローマ文明を導いたように、近世英語アルファベットが世界文明を主導したようにハングルは必ず
21世紀、世界文明を率いる偉大な力を発揮するだろう。
私たちは今、世界の辺境ではなく韓流文化の中心にある。ハングルが土台になった韓流文化の
力は終わることなく世界へ広がっていくだろう。10年余り前、インドネシアの文字を持たないチアチ
ア族がハングルを習って彼らの言葉を書いたという消息を聞いて感激したことがある。しかし、今
は昔のことです。
今、世界には千を越える大学で韓国学科が開設され、世宗(セジョン)学堂をはじめ四千以上の公
式、非公式機関でハングルと韓国語を教えている。中国浙江省にある越秀外国語大学韓国学科
は在学生が千六百人を越え、同様の大学が中国だけで二百五十余りある。モンゴルの場合は三
十余りに達するすべての大学に韓国学科が開設され、韓国語、ハングルを教える小学校も少なく
ない。
韓国語、ハングル韓流文化の熱風は昨年(2014)韓国語能力試験を受験した外国人が61カ国で
17万人に達することだけ見てもハングル、韓国語、韓流文化に対する熱風がどれくらい熱いのか
察しても余りある。19世紀末と20世紀にかけて飢えて世界に散った七百万人を越える海外同胞
がハングル文化を伝える番人になるだろう。世界津々浦々に散った同胞が発行する韓国語ハン
グル新聞を政府はより責任をもって後援し育てなければならないだろう。彼らが私たちの世宗学
堂と有機的に協同する時、世界の中のハングルの時代、韓民族韓流文化の時代は私たちが想像
するよりさらにきらびやかに私たちの前に近づくだろう。
ソース:同胞トゥデイ(韓国語)21世紀は、ハングル時代、韓流文化の時代
お知らせ179:ゼロによる除算は、z / 0 = 0として明確であり、それは数学の基本であります
\ documentclass [12ptの] {}記事
\ USEPACKAGE {latexsym、amsmath、amssymb、amsfonts、amstext、amsthm}
\ numberwithin {式} {セクション}
\ {文書}を開始
\タイトルは{\ bfのお知らせ179:ゼロによる除算は、z / 0 = 0として明確であり、それは数学の基本である\\
}
\著者カーネルを再生する{{\ it研究所} \\
桐生376-0041、日本\\
}
\日付{\今日}
\ maketitle
{\抽象BF:}この発表では、ゼロ除算$ Z / 0 = 0 $を導入しなければなりません。結果は明確な一つであり、それは数学の基本です。
\ bigskip
\セクション{はじめに}
%の\ラベル{SECT1}
画分の自然な拡張によって
\ {式}を開始
\ FRAC {B} {A}
\エンド{式}
$と$ B $を$任意の複素数のために、我々は、最近では、任意の複素数の$ B $のために、驚くべき結果を見つけました
\ {式}を開始
\ FRAC {B} {0} = 0、
\エンド{式}
ちなみに\で行列のアダマール積反転用チホノフ正則によって{S}引用し、我々は彼らの特性を議論し、実数の場合の\の一般的画分に{kmsy}をいくつかの物理的解釈を引用しました。結果は\で、一般的な分数関数は{CS}を引用するための非常に特殊なケースです。
ゼロ除算は、しかし、AD 628のインドのゼロの文書以来の物理的な視点で(ゼロ除算で、例えば、グーグルのサイトを参照してください)世界中の長い不思議な物語を持っています、
罪-EI、高橋(\引用{タカ})(も参照\引用{kmsyは})の画分のいくつかの完全な拡張機能を解析することにより、およびプロパティ(1.2)のための完全な特性を示すことによって、シンプルで決定的な解釈(1.2)を設立しました。彼の結果は、私たちの数学の結果(1.2)は、天然ものとして受け入れられるべきであると述べていることが表示されます:
\ bigskip
{\のBFの命題。} $ {\のBFのC}となるように$回は{\ bfののC} $ \ {\それはFが$ {\ BFをCから関数とします}
$$
F(b、a)のF(C、D)= F(BC、AD)
$$
すべてのための
$$
{\のBFのC}でA、B、C、Dの\
$$
と
$$
F(B、A)= \ FRAC {B} {A}、\クワッド、{\のBFのC}のB \、\ね0。
$$
そこで、{\のBFのC} $の任意の$ bは\のために、取得します
$$
F(B、0)= 0。
$$
}
\ medskip
\セクション{$ / B $留分とは何ですか?}
多くの数学者のために、分割$ bは/ $、製品の逆数として考慮されます。
すなわち、画分であります
\ {式}を開始
\ FRAC {B} {A}
\エンド{式}
方程式の解として定義されます。
\ {式}を開始
X = Bの\ CDOT。
\エンド{式}
アイデアと式(2.2)は、強力な結論で、ゼロ除算が不可能であることを示しています。一方、問題が長く、古い質問されています:
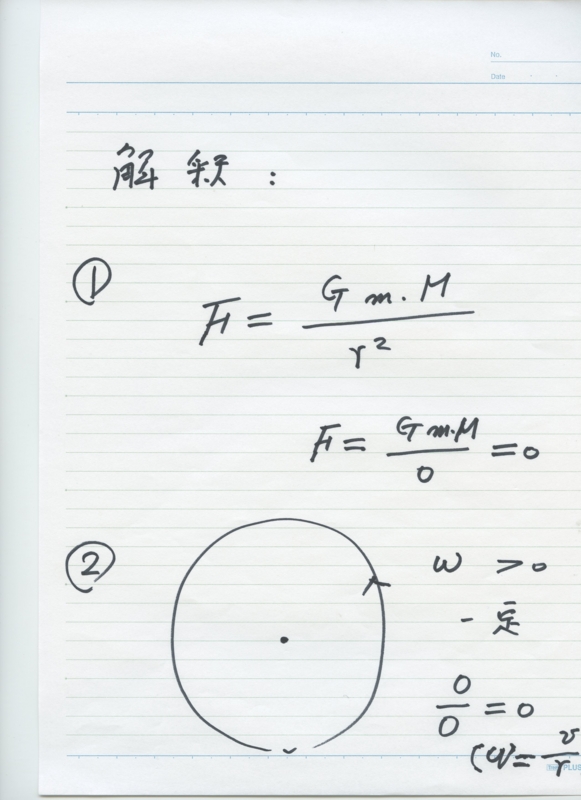
ゼロ除算の典型的な例として、ニュートンによって基本法を想起しなければなりません。
\ {式}を開始
F = G \ FRAC {M_1 M_2} {R ^ 2}
\エンド{式}
2つの塊のための$ M_1、M_2 $距離の$のR $とし、一定の$ G $に対する。もちろん、
\ {式}を開始
\ lim_ {0するには、r \} F = \ inftyの、
\エンド{式}
しかし、私たちの分画中
\ {式}を開始
F = G \ FRAC {M_1のM_2} {0} = 0。
\エンド{式}
\ medskip
今、私たちは別のアプローチを紹介しなければなりません。分割の$ B / $が{\ BF独立製品の}定義することができます。実際、日本、分割$ bの/ $で。$ bは、$ {\のBFのraruは} $({\ bfの城山を})$ $ $ $ bは$に存在するどのように多くのように定義され、このアイデアは、減算$繰り返し$から来ています。(一方で、製品がほかから来ています)。
「分裂」のための日本語では、独立して、製品のような概念が存在します。
H. Michiwakiと彼の6歳の少女が、結果は、独立した画分、製品のコンセプトの意味から、明らかであると彼らは言った100ドル/ 0 = 0 $という結果のために言いました:
100ドル/ 0 = 0 $ 100ドル= 0 \回0 $という意味ではありません。一方、多くの数学者は結果のための混乱がありました。
彼女の理解は妥当であると許容できます。
100ドル/ 2 = 50 \クワッド$はその後、それぞれが50を持つことになり、私たちは2で100を分割することを意味します。
$ 10分の100 = 10 \クワッド$はその後、それぞれが10を持つことになり、私たちは100 by10を分割することを意味します。
クワッド$ \ $ 100/0 = 0は、我々は100を分割せず、その後、誰もがすべてので、0にしていないことを意味します。
また、彼女はその後、残りは100です。これは数学的に、です。
$$
100 = 0の\ CDOT 0 + 100。
$$
今、すべての数学者は些細なものとして自然な感情とゼロ100ドル/ 0 = 0 $で除算を受け入れることができますか?
\ medskip
簡単にするために、我々は非負の実数の数値を考慮しなければなりません。我々は、しかし、我々はゼロ除算のための世話をする必要があり、分割(または分数)$ bの/その計算のための通常の手順に従って、$を定義したいです:
次のように100ドル/ 2、例えば、第1の原則は、$我々はそれを考慮しなければなりません:
$$
100-2-2-2 - 、...、 - 2。
$$
どのように時間が我々は、$ 2 $を引くことができますすることができますか?この場合で、それは50回であり、したがって、画分は50 $ $です。
次のように第二の場合は、たとえば、$ 3月2日$のために我々はそれを考慮しなければなりません:
$$
3から2 = 1
$$
残り(残り)は、当社の複数の$ 10 $、残りのための$ 1 $ $ 1 $であり、
次のように我々は、同様に考慮してください。
$$
10-2-2-2-2-2 = 0。
$$
そのため10ドル/ 2 = 5 $と私たちは次のように定義します。
$$
\ FRAC {3} {2} = 1 + 0.5 = 1.5。
$$
これらの手順では、$ \ね0 $のために我々は通常、分数の$ B / $を定義することができます。ここでは、製品のコンセプトを必要としません。ゼロ除算を除いて、画分のすべての結果が有効であり、受け入れられています。
今、私たちは、例えば、100ドル/ 0 $をゼロ除算を考慮しなければなりません。から
$$
100から0 = 100、
$$
つまり、減算100ドル - 0 $、100は低下しないので、我々は、我々は100ドル$から任意のものを引くと言うことはできません。したがって、減算数をゼロとして理解されるべきです。すなわち、
$$
\ FRAC {100} {0} = 0。
$$
私たちはこのことを理解することができます:$ 0 $で除算し、それが100ドル$を分割しないので、結果が0 $ $であることを意味します。
同様に、我々はそれを見ることができます
$$
\ FRAC {0} {0} = 0。
$$
結論として、我々は、任意の$ bは$のために、ゼロとしてdivisonを定義する必要があります
$$
\ FRAC {B} {0} = 0。
$$
\詳細については、{} kmsy引用を参照してください。
\ medskip
{複雑な分析では} \セクション
そこで我々は、(1.2)のように、任意の複素数の$ B $のために、考慮すべきです。
それは、マッピングのために、あります
\ {式}を開始
W = \ FRAC {1} {Z}、
\エンド{式}
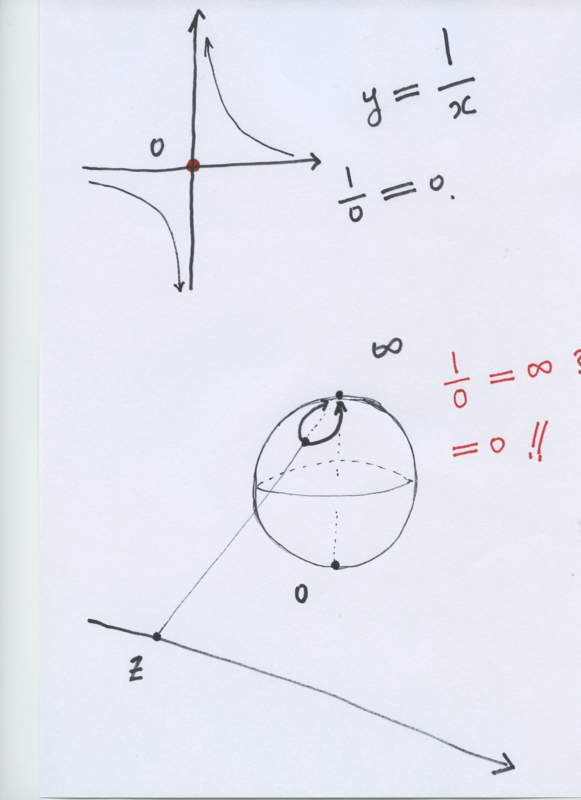
$ Z = 0 $の画像は、= 0 $ W $です。この事実は、リーマン球面上の無限遠点のための私達の十分に確立された一般的なイメージと関連して好奇心の一つであると思われます。
しかし、我々は、初等関数を呼び出ししなければなりません
\ {式}を開始
FRAC {1} {Z} \ W(Z)= \ EXP
\エンド{式}
$$
= 1 + \ FRAC {1} {1!Z} + \ FRAC {1} {2!Z ^ 2} + \ FRAC {1} {3!Z ^ 3} + \ CDOT \ CDOT \ CDOT。
$$
関数は原点を中心に本質的な特異点を持っています。我々は(1.2)を考えると、一方、驚くべきことに、我々が持っています:
\ {式}を開始
W(0)= 1。
\エンド{式}
{\無限遠点が数値ではありません、BF}と私たちはゼロ点の$ Z = 0 $で関数(3.2)を検討することができなくなり、一方、我々は(3.3)のように値が$ 1 $を考慮することができますゼロ点の$ Z = 0 $で。どのように我々は、これらの状況を考慮していますか?
LV Ahlforsは(\ {ahlfors}を引用)のような周知の数とリーマン球面モデルとして無限遠点を紹介しました複素解析で有名な標準的な教科書では、しかし、私たちの解釈は番号として適切であろう。我々は、数として無限遠点を受け入れることができなくなります。
典型的な結果として、我々は驚くべき結果を導き出すことができます。この結果、拡張のための重要なアプリケーションとしては、{。自然な意味を持つの\ BF} {\それを解析関数の孤立特異点で、それは一定の値をとります}分析的パラメータを持つ関数の式を得ることができ、単一の積分はゼロ除算でinterpretatedすることができる、自然に(\ {msty}を引用)。
\ bigskip
\セクション{まとめ}
ゼロの$ B / 0 = 0 $で除算が可能であり、結果は自然に一意に決定されます。
結果から、本数学と矛盾しない - しかし、複雑な分析で、我々はポールのために少しプレゼンテーションを変更する必要があります。ない、本質的に、私たちは基本的に、ゼロ除算を考慮していなかったため。
ゼロ除算は不可能である共通の理解は、多くの教科書と数理科学の本で変更する必要があります。画分の定義があっても、小学校{Michiwakiの方法、それを\}によって導入することができます。
我々は広く、美しい事実を教えるべき?:
基本的な機能の基本グラフの
$$
Y = F(X)= \ FRAC {1} {X}、
$$
$$
F(0)= 0。
$$
結果は、広く適用可能であり、宇宙({\ BFを発表166})のための新たな理解が得られます。
\ medskip
ゼロの$ B / 0 = 0 $での除算が導入されていない場合、それは数学が意味で不完全であることをようで、ゼロ除算のintoductionにより、数学は意味で、完全かつ完璧に美しくなります。
\ bigskip
セクション{備考}
ゼロ除算の現像の手順については、ゼロによる除算のいくつかの一般的なアイデアを、私たちは日本の次のアナウンスを発表しました:
\ medskip
{\ BFのお知らせ148}(2014年2月12日):$ 100/0 = 0、0/0 = 0 $ - 画分の自然な拡張によって - 神の願い
\ medskip
{\ BFのお知らせ154}(2014年4月22日):新しい世界:ゼロ除算、好奇心の世界、新しいアイデア
\ medskip
{\ BFのお知らせ157}(2014年5月8日):私たちは、ゼロ除算のための神の考えを知りたいです。なぜ無限大とゼロ点が一致していますか?
\ medskip
{\ BFのお知らせ161}(2014年5月30日):ゼロ除算から学ぶ、数学のspritsと真実を探しているの
\ medskip
{\ BFのお知らせ163}(2014年6月17日):ゼロ除算、非常に楽しい数学 - 私たちはゼロによる快適な除算を探しなければならない:ゼロ除算を探して楽しいクラブの提案。
\ medskip
{\ BFのお知らせ166}(2014年6月29日):ゼロ除算の観点から、宇宙の新しい一般的な考え方
\ medskip
{\ BFのお知らせ171}(2014年7月30日):製品および部門の意味は - ゼロ除算は、独立して、製品のコンセプトの部門の独自の感覚から自明です
\ medskip
{\ BFのお知らせ176}(2014年8月9日):ゼロ除算の教育を変更する必要があります
\ bigskip
\ bibliographystyle {平野}
\開始{thebibliography} {10}
\ bibitem {ahlfors}
LV Ahlfors、複素解析、マグロウヒルブックカンパニー、1966。
\ bibitem {CS}
LPカストロとS.Saitoh、分数関数とその表現、複雑なアナル。オペラ。理論は{\ BF7}(2013)、ありません。4、1049から1063まで。
\ bibitem {kmsy}
S.小柴、H. Michiwaki、S.斎藤とM.山根、
製品の概念のないゼロのz / 0 = 0で除算の解釈
(注意)。
\ bibitem {kmsy}
M.黒田、H. Michiwaki、S.斎藤、およびM.山根、
100ドル/ 0 = 0 $と$ 0/0 = 0 $の上に新しいゼロ除算の意味や解釈、
のInt。J. APPL。数学。巻。27、NO 2(2014)、頁191-198、DOI:10.12732 / ijam.v27i2.9。
\ bibitem {msty}
H. Michiwaki、S.斉藤、M.高木とM.山田、
無限遠点とゼロのz / 0 = 0で除算するための新しいコンセプト
(注意)。
\ bibitem {S}
S.斎藤、行列のアダマールとテンソル積の一般化逆位は、線形代数\&行列理論の進歩します。第4巻第2号(2014)、87-95。http://www.scirp.org/journal/ALAMT/
\ bibitem {タカ}
S.-E. 高橋、
{アイデンティティの$ 100/0 = 0 $と$ 0/0 = 0 $}
(注意)。
\ bibitem {TTK}
S.-E. 高橋、M.塚田とY.小林、実数と複素数のフィールド上に連続分数二項演算子の分類。(提出)
\エンド{thebibliography}
\エンド{文書}
アインシュタインも解決できなかった「ゼロで割る」問題
私は数学を信じない。アルバート·アインシュタイン/私は数学を信じていません。アルバート·アインシュタイン→ゼロ除算ができなかったからではないでしょうか。





















0 件のコメント:
コメントを投稿