5000年前の古代エジプトのペット事情が明らかに
ゾウ、ヒョウ、カバ、ワニ、ヒヒなど、埋葬された骨の分析から
2015.05.28
ヒエラコンポリスにある古代墓地の富裕市民の墓のそばには、ヒヒなどの珍しい動物たちの骨が埋まっていた。(Photograph by Renee Friedman, Courtesy of Hierakonpolis Expedition)
[画像のクリックで拡大表示]
古代エジプト人にとって、異国の珍しい動物を所有することは富と力を誇示する手段だった。しかしナイル川付近の墓地に5000年以上前に埋葬されたヒヒやカバの骨からは、地位の象徴として飼われていた動物たちの悲惨な生活が垣間見える。
NG MAPS SOURCES: ANCIENT WORLD MAPPING CENTER AND INSTITUTE FOR THE STUDY OF THE ANCIENT WORLD
[画像のクリックで拡大表示]
ある墓から見つかったヒヒの骨格には、粉々になった手足の骨が含まれており、これは彼らが罰として叩かれていたことを示唆している。少なくとも2匹のヒヒが腕の骨を折られているが、こうした傷は頭を叩かれるのを防ごうとしたときにできることが多い。ほかにもつながれた縄から逃れようとしたせいで足が折れたカバの子供や、縄でつながれていたことが原因と見られる傷を持つアンテロープと野生の牛の骨も発見された。
古代エジプトの飼育係が「こうした動物の世話に手を焼いていたのは明らかです」。動物たちの骨の分析結果についての論文を、骨考古学専門誌『International Journal of Osteoarchaeology』の次号に発表するベルギー王立自然史博物館の動物考古学者ビム・バン・ネール氏はそう語る。「動物を飼育する技術は、現代ほど発達していなかったのです」
今回の調査対象となった動物の骨が見つかったのは、ファラオによる統一王国が成立するずっと以前のエジプトで繁栄した、ヒエラコンポリスという町の古代墓地だ。発掘調査により、富裕層の市民を埋葬した墓のそばから、ゾウ2頭、ヒョウ1頭、ワニ2匹の骨格の他、異国の動物9匹の骨の一部が見つかった。古代エジプトで人に飼われていた動物の骨が、これほど大量に見つかったのは初めてのことだ。この動物たちはおそらく、飼い主が死んだ後に生贄として殺されたのだろう。(参考記事:「エジプト先王朝時代の墓地を発掘」)
オスのゾウの骨を発掘する作業員。大きく力強いゾウと、彼らを所有する支配者たちは、どちらも人々の畏怖の対象だった。(Photograph by Renee Friedman, Courtesy of Hierakonpolis Expedition)
[画像のクリックで拡大表示]
ペットは語る
ヒエラコンポリス調査団の代表で、過去にはナショナル ジオグラフィックから研究支援を受けていたこともあるレネー・フリードマン氏によると、古代エジプトの人々は、みずからが所有する動物たちにさまざまな意味を見出していたという。エジプトの支配者たちは、ゾウの力強さに憧れていたことだろう。一方、カバは恐ろしい破壊の象徴だ。カバを所有することは「本当に無秩序な自然の力を支配していることを意味します」とフリードマン氏は言う。
動物の骨に残った傷には治癒の痕跡があることから、彼らが怪我をした後すぐには殺されず、少なくとも数週間は生かされていたことがわかる。米ミシガン大学ケルシー博物館の考古学者で、エジプトで発掘された古代の動物の骨を研究した経験のあるリチャード・レディング氏によると、動物たちがどの時点で怪我をしたのかは正確にはわからないものの、おそらくは捕まえられる際に暴れたことが原因ではないかという。
ヒエラコンポリスの墓地から見つかる動物たちは、おそらくは所有者が死亡した際、死後の世界まで供をするために生贄にされたのだろう。(Photograph by Renee Friedman, Courtesy of Hierakonpolis Expedition)
[画像のクリックで拡大表示]
バン・ネール氏もまた、人間が動物を捕まえるときに怪我をさせた可能性があると考えている。しかし「墓所12」と名付けられた場所で見つかったヒヒの四肢の先端の骨は、40以上の破片に砕かれており、捕獲の際に負った怪我とはとうてい思えない。人間の手から逃げようと暴れた場合には、むしろ四肢の長骨が折れる可能性が高い。
またネール氏によると、これより後の時代に飼われていたヒヒのミイラには、手荒い扱いを受けた痕跡がほとんど見られないという。その頃には古代エジプトの人々も、叩いたり縄でしばったりすることなく動物を扱う方法を学んだのではないだろうか。ヒエラコンポリスにおいても、「墓所12」よりも新しい墓から見つかるヒヒには、暴力を振るわれた痕跡が少ないそうだ。
「ヒヒの扱いは簡単ではありません。ヒヒは人に噛み付き、物を盗む危険な動物です」とネール氏は言う。ヒヒを初めて飼ったエジプト人は、殴りつけることでおとなしくさせようとしたのだろうが、じきにその扱い方をマスターしていったようだ。
文=Traci Watson/訳=北村京子http://natgeo.nikkeibp.co.jp/atcl/news/15/052700118/
Announcement 213: An interpretation of the identity $ 0.999999...... =1$
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 213: An interpretation of the identity $ 0.999999...... =1$
}
\author{{\it Institute of Reproducing Kernels}\\
\date{}
\maketitle
{\bf Abstract: } In this announcement, we shall give a very simple interpretation for the identity: $ 0.999999......=1$.
\bigskip
\section{ Introduction}
On January 8, 2008, Yuusuke Maede, 8 years old boy, asked the question, at Gunma University, that (Announcement 9(2007/9/1): Education for genius boys and girls):
What does it mean by the identity:
$$
0.999999......=1?
$$
at the same time, he said: I am most interesting in the structure of large prime numbers. Then, a teacher answered for the question by the popular reason based on the convergence of the series: $0.9, 0.99, 0.999,... $. Its answer seems to be not suitable for the 8 years old boy with his parents (not mathematicians). Our answer seems to have a general interest, and after then, such our answer has not been heard from many mathematicians, indeed.
This is why writting this announcement.
\medskip
\bigskip
\section{An interpretation}
\medskip
In order to see the essence, we shall consider the simplist case:
\begin{equation}
\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + ... = 1.
\end{equation}
Imagine a tape of one meter length, we will give its half tape: that is,
\begin{equation}
\frac{1}{2}.
\end{equation}
Next, we will give its (the rest's half) half tape; that is, $\frac{1}{2}\cdot \frac{1}{2} = \frac{1}{2^2}$, then you have, altogether
\begin{equation}
\frac{1}{2} + \frac{1}{2^2} .
\end{equation}
Next, we will give the last one's half (the rest's half); that is, $\frac{1}{2}\cdot \frac{1}{2} \cdot \frac{1}{2}= \frac{1}{2^3}$,
then, you have, altogether
\begin{equation}
\frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3}.
\end{equation}
By this procedure, you will be able to obtain the small tapes endressly. Imagine all the sum as in the left hand side of (2.1). However, we will see that this sum is just the division of the one meter tape. Therefore, we will be able to confim the identity (2.1), clearly.
The question proposed by Y. Maede is just the small change the ratio $\frac{1}{2}$ by $\frac{9}{10}$.
\bigskip
\section{ Conclusion}
Y. Maede asked the true sense of the limit in the series:
$$
0.999999.....
$$
that is, this series is approaching to 1; however, is it equal or not ? The above interpretation means that the infinite series equals to one and it is just the infinite division of one. By this inverse approarch, the question will make clear.
\medskip
\bigskip
\section{Remarks}
Y. Maede stated a conjecture that for any prime number $p$ $( p \geqq 7)$, for $1$ of $ - 1$
\begin{equation}
11111111111
\end{equation}
may be divided by $p$ (2011.2.6.12:00 at University of Aveiro, by skype)
\medskip
(No.81, May 2012(pdf 432kb)
www.jams.or.jp/kaiho/kaiho-81.pdf).
\medskip
This conjecture was proved by Professors L. Castro and Y. Sawano,
independently. Y. Maede gave later an interesting interpretation for his conjecture.
\medskip
(2015.2.26)
\end{document}
Announcement 214: Surprising mathematical feelings of a 7 years old girl
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 214: Surprising mathematical feelings of a 7 years old girl
}
\author{{\it Institute of Reproducing Kernels}\\
\maketitle
{\bf Abstract: } In this announcement, we shall give the two surprising mathematical feelings of 7 years old girl Eko Michiwaki who stated the division by 3 of any angle and the division by zero $100/0=0$ as clear and trivial ones. As well-known, these famous problems are historical, and her results will be quite original.
\bigskip
\section{ Introduction}
We had met, 7 years old girl, Eko Michiwaki on November 23, 2014 at Tokyo Institute of Technology and August 23, 2014 at Kusatu Seminor House, with our colleagues. She, surprisingly enough, stated there repeatedly the division by 3 of any angle and the division by zero $100/0=0$ as clear and trivial ones. As well-known, these famous problems are historical and her results will be quite original.
\section{The division of any angle by 3}
\medskip
Eko Michiwaki said:
divide a given angle with 4 equal angles; this is simly done. Next, we divide one divided angle
with 4 equal angles similarly and the three angles add to other 3 angles. By continuing this procedure, we will be able to obtain the division by 3 of any angle. Her idea may be stated mathematically as follows:
$$
\frac{1}{4} + \frac{1}{4^2} + \frac{1}{4^3} + ... ...= \frac{1}{3}.
$$
However, her idea seems to be more clear than the above mathematical formula. For this sentence, see \cite{ann3} for the sense of the limit.
\bigskip
\section{The division by zero $100/0=0$}
\medskip
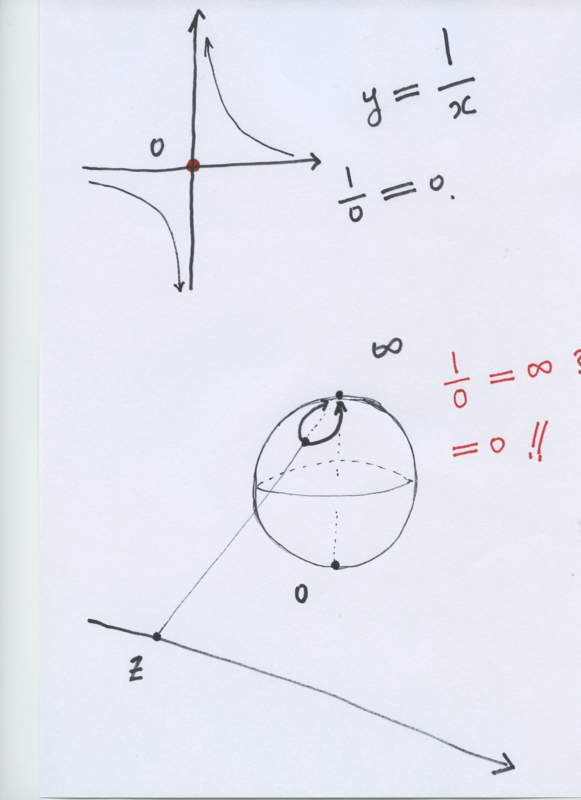
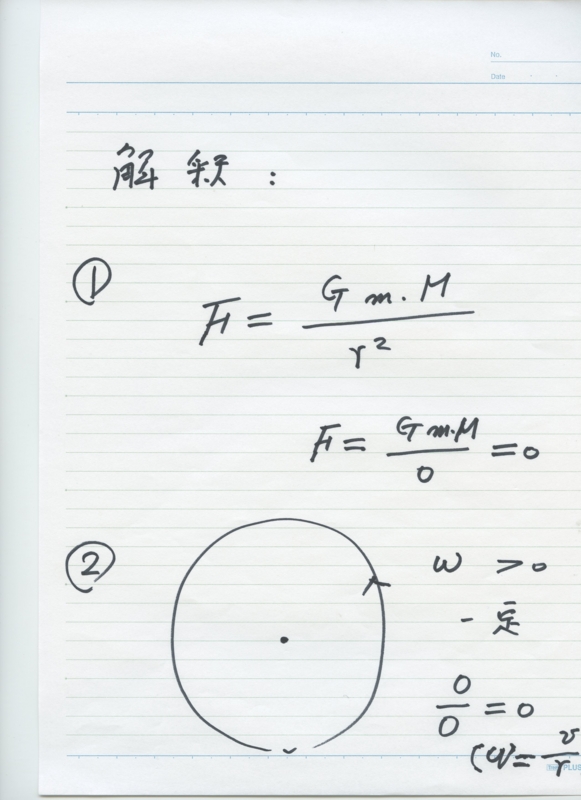
As we stated in \cite{ann1}, she stated that division by zero $100/0=0$ is clear and trivial for our recent results \cite{cs,kmsy,s,ttk}. The basic important viewpoint is that division and product are different concepts and the division by zero $100/0=0$ is clear and trivial from the own sense of the division, independently of product \cite{ann1}. From the viewpoint, our colleagues stated as follows:
\medskip
On July 11, 2014, Seiichi Koshiba and Masami Yamane said at
Gunma University:
The idea for the division of Hiroshi Michiwaki and Eko Michiwaki (6 years
old daughter) is that division and product are different concepts and they
were calculated independently for long old years, by repeated addition and
subtraction, respectively. Mathematicians made the serious mistake for very
long years that the division by zero is impossible by considering that division
is the inverse operation of product. The division by zero was, however, clear
and trivial, as z/0=0, from the own nature of division.
\medskip
On February 21, 2015, Seiichi Koshiba and Masami Yamane visited our Institute and we confirmed this meaning of these sentences and the basic idea on the division by zero.
\medskip
(2015.2.27)
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{cs}
L. P. Castro and S.Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances inLinear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95.http://www.scirp.org/journal/ALAMT/
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics (in press).
\bibitem{ann1}
Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics,
Institute of Reproducing Kernels, 2014.10.22.
\bibitem{ann2}
Announcement 185: The importance of the division by zero $z/0=0$, Institute of Reproducing Kernels, 2014.11.28.
\bibitem{ann3}
Announcement 213: An interpretation of the identity $ 0.999999...... =1$, Institute of Reproducing Kernels, 2015.2.26.
\end{thebibliography}
\end{document}





















0 件のコメント:
コメントを投稿