2018年5月23日水曜日

チューリング機械からコンピュータの原理を学ぶ

チューリング機械からコンピュータの原理を学ぶ

現在のコンピュータ・サイエンスの源流をたどると，チューリング機械に行き当たります。チューリング機械から現在のコンピュータ・サイエンスの数多くの分野が生まれました。計算機の設計理論であるアーキテクチャー，自然言語解析，人工知能……などです。チューリングの創設した理論の概要をわかりやすく紹介します。

人工知能の誕生とアラン・チューリング

はじめてコンピュータの原理を考案したのは，イギリスの数学者アラン・チューリング（1912〜1954）でした。電卓さえもなかった時代にコンピュータの原型である“⁠チューリング機械⁠”は考案されたのです。
チューリングは，1936年の論文で仮想的な計算機を作り上げました。チューリングが考えた“⁠チューリング機械⁠”はとても単純な構造ながらも，誰も思いつかないような独創的な計算機モデルでした。この計算機モデルはコンピュータの仕組みの核となる原理をついており，それを深く知ることで現在のコンピュータの能力を理解することができます。さらに，コンピュータにはできないこと……つまり能力の限界をも知ることができるのです。
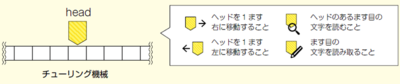
チューリング機械の驚嘆すべきところは，その極端なまでの単純さです。1本のテープと読み取りヘッドが1つあるだけです。そして出来ることは，ヘッドを右か左に1文字分移動することと，テープに文字を書き込むこと，そして文字を読み取ることのみです。これだけの機構で，アルゴリズムすべてが実現できるのです。
図1　チューリング機械の概念
図1　チューリング機械の概念
これほどまでに単純でほんの少しの操作しかできない機械でありながら，チューリング機械は現在のコンピュータが行う，どんな計算も模倣することができます。ここで注意していただきたいのは，この機械は機械と名はついていますが，“⁠物理的な構造⁠”はありません。ヘッドの素材は木だとか，テープの素材は紙だ，といった材料の概念は存在しません。どのように計算が行われるかを想定した，頭の中で作り上げた架空の装置です。

コンピュータは“不可能への挑戦”の副産物だった

チューリングがチューリング機械を考案した本来の目的は，“⁠コンピュータを作るため⁠”ではありませんでした。チューリングが計算機モデルの論文を発表したのは今から80年以上も前になりますが，その当時の多くの数学者に影響を与え，20世紀の数学研究の方向を示した数学者にダフィット・ヒルベルト（1862年〜1943年）という人物がいます。
ヒルベルトは数学というシステムを整えるべく「その数学が絶対に間違わないということを数学的に証明しよう」という運動を始めました。数学を厳密に公理化しようとするプログラムで，ヒルベルト・プログラムとして知られています。ヒルベルト・プログラムの究極の目的は，次のことを行なうことでした。
数学の命題を論理式として表す。その論理式が正しいかどうか，言い換えると，その論理式が定理かどうかを，数学的に論証するアルゴリズムを開発すること。
この問題を「決定問題」といいます。チューリングはこの問題を解くためにチューリング機械を発明したのです。
1900年8月，ヒルベルトはパリで開催された国際数学者会議で，20世紀の数学者に向けて23題の未解決問題を提示しました。その中の第10問題は「ディオファントス方程式を解くアルゴリズムを見つけよ」というものでした。23題の未解決問題は次々に解かれていきましたが，第10問題は長きにわたり未解決のままで，多くの数学者が第10問題に魅了されその問題の解決に取り組みました。そしてついに提示から70年後にロシアの数学者ユーリ・マチャセビッチによって「ディオファントス方程式を解くアルゴリズムはない（計算不能だ）⁠」という否定的な結論が出されました。その結論が導き出されたのは，紛れもなくチューリング機械とチューリングが定義した『計算不能』という概念があったからです。ディオファントス方程式は古代ギリシア時代からある有名な整数係数の方程式で，その問題にアルゴリズムがないなどとは誰も信じられない結果でした。
チューリングがチューリング機械で示したのは，「⁠ヒルベルト・プログラムの決定問題を解くアルゴリズムは存在しない」ということでした。この結論はヒルベルト・プログラムを破綻に導いたとか機械の蹉跌とよく言われていますが，果たしてそうでしょうか。チューリング機械や『計算不能』という概念が，第10問題の解決に繋がっていったように，コンピュータ・サイエンスは衰えるどころか現在のコンピュータの原理を生み出し，コンピュータ・サイエンスの発展に繋がっていきました。自身の業績がもとになり，現代のようなコンピュータの世界になっていくとは，チューリング自身も想像していなかったでしょう。

プログラム内蔵方式

当時の機械は，ある特定の目的のために作られており，異なるプログラムで動く機械は異なる機械としてそのつど構成していました。チューリングはこの意味で，何種類ものチューリング機械を考案しています。中でも特に素晴らしく画期的で優れた機械は，万能チューリング機械だと言えるでしょう。万能チューリング機械の素晴らしさはその汎用性にあります。万能チューリング機械1つあれば，全ての目的を実行することができるのです。
万能チューリング機械はプログラム「P」を入力データ「x」と共に受け取ります。プログラム「P」を入力値と一緒に受け取ることで，異なるプログラムを実行する時に新しく機械を構成する必要がなくなります。この万能チューリング機械は，現在ではプログラム内蔵方式と呼ばれ，実際のコンピュータの誕生の大きな礎となりました。
コンピュータ学界の大御所であり実際のコンピュータの開発を数多く手掛けた巨人にフォン・ノイマンという数学者がいます。彼は万能チューリング機械を高く評価しており，コンピュータの父と称えられたとき，「⁠私はただの助産師にすぎない」と答えていたそうです。チューリング機械は，当時の数学界を牽引する人々に高く評価されていたのです。
さらに注目すべき点として，万能チューリング機械は現在のコンピュータと同等の能力を持っているといえます。等価性については明確な定義や議論が必要となりますが，ここでは万能チューリング機械は現在のコンピュータができる全ての計算をシミュレートできると考えてください。そして驚くべきことに，現在のコンピュータの能力だけでなく，未来に出てくるであろう全てのコンピュータの能力とも等価であるとされています。
この議論においてはコンピュータの処理速度やメモリ容量などは含みません。現在のコンピュータ開発においては外すことができない観点ではありますが，コンピュータの能力の本質を知るために，ここでは商業的な条件は削ぎ落とし，学術的・原理的な観点から考えています。

コンピュータにも計算できない問題がある

ヒルベルトの「決定問題」を解くためにチューリング機械は考案されましたが，チューリングが導き出した答えは『決定問題を解くアルゴリズムは存在しない』という否定的ともとれる結果でした。アルゴリズムがないということは，コンピュータで計算できないと言い換えることができます。これはコンピュータの能力の限界をも指し示すものであり，当時はとてもショッキングな結論でした。しかし，その結果は『アルゴリズムとはなにか』『⁠計算とはなにか』という数学の基本原理の追及に繋がっていきました。
例えば，アルゴリズムをどのように表現するかという問題は，プログラミング言語の研究に発展していきます。また，チューリング機械をモデルとしてオートマトン理論と呼ばれる脳のモデルの研究へも繋がっていきます。不思議なことに数学というのは，あるいは科学一般に言えることかもしれませんが，『⁠できない』という否定的な結果が，多くのものを生み出すきっかけになることが多いように思われます。
チューリングが論文を発表した1936年，アロンゾ・チャーチはすでにこの問題を解いていました。チャーチは「アルゴリズムとはなにか」という点で，チューリングとは違う考えを持っていましたが，「⁠決定問題は計算できない」という同じ結論に達していました。当時のチューリングの指導教官の優れたところは，同じ結論を導き出したチューリングの論文の素晴らしさを認め，この論文をチャーチに紹介したところです。チャーチもすぐにこの論文の素晴らしさを認めています。これが「チャーチ=チューリングの定立」と呼ばれているものです。

チューリングは問う「機械は考えることができるだろうか？」

チューリングが行なったテストは次のようなものでした。「⁠人間が機械に対して質問をします。機械から返事がかえってきます。対話相手がコンピュータであると判断できなければ，コンピュータには知性があるとします。」これはチューリングテストと呼ばれ，現在でも議論の対象となっています。チューリングは人工知能の概念も研究を進め「考えるとはなにか」「⁠知性とはなにか」といった議論を展開していきました。
近年，ニュースや新聞などで人工知能という言葉をよく耳にします。ある一面において最先端の技術とも取られがちですが，それは今に始まったことではなく，チューリングの時代から研究されていました。実際，チューリングは1950年に「計算機と知能」という記事の中でこのチューリングテストについて言及しています。
チューリングは計算する機械を生みだし，脳はコンピュータかということにまで研究を広げていきました。コンピュータの世界は日進月歩ですが，未来に出てくるであろう，どんな機械よりも強力な計算機モデルは80年以上も前に誕生しました。人工知能の概念もまた，フォン・ノイマンやチューリングの時代からすでに研究されています。古い時代のコンピュータ・サイエンスの世界を読み解くことで，新しい見地が得られるかもしれません。

著者プロフィール

阿部彩芽（あべあやめ）

グラフィックデザイナー・イラストレーター・webデザイナー
大阪大学工学部を卒業後，同大学大学院に進学。創造社デザイン専門学校にて広告デザインを学ぶ。その後，東京の広告制作会社にてグラフィックデザイナーとして勤務。現在は独立し，フリーランスとして活動。http://gihyo.jp/book/pickup/2018/0032

ゼロ除算の発見は日本です：

∞？？？
∞は定まった数ではない・・・
人工知能はゼロ除算ができるでしょうか：

とても興味深く読みました：
ゼロ除算の発見と重要性を指摘した：日本、再生核研究所


ゼロ除算関係論文・本



再生核研究所声明 411(2018.02.02): 　ゼロ除算発見4周年を迎えて

ゼロ除算100/0=0を発見して、４周年を迎える。　相当夢中でひたすらに　その真相を求めてきたが、一応の全貌が見渡せ、その基礎と展開、相当先も展望できる状況になった。論文や日本数学会、全体講演者として招待された大きな国際会議などでも発表、著書原案１５４ページも纏め（http://okmr.yamatoblog.net/）基礎はしっかりと確立していると考える。数学の基礎はすっかり当たり前で、具体例は７００件を超え、初等数学全般への影響は思いもよらない程に甚大であると考える：　空間、初等幾何学は　ユークリッド以来の基本的な変更で、無限の彼方や無限が絡む数学は全般的な修正が求められる。何とユークリッドの平行線の公理は成り立たず、すべての直線は原点を通るというが我々の数学、世界であった。y軸の勾配はゼロであり、\tan(\pi/2) =0　である。　初等数学全般の修正が求められている。
数学は、人間を超えたしっかりとした論理で組み立てられており、数学が確立しているのに今でもおかしな議論が世に横行し、世の常識が間違っているにも拘わらず、論文発表や研究がおかしな方向で行われているのは　誠に奇妙な現象であると言える。ゼロ除算から見ると数学は相当おかしく、年々間違った数学やおかしな数学が教育されている現状を思うと、研究者として良心の呵責さえ覚える。
複素解析学では、無限遠点はゼロで表されること、円の中心の鏡像は無限遠点では　なくて中心自身であること、ローラン展開は孤立特異点で意味のある、有限確定値を取ることなど、基本的な間違いが存在する。微分方程式などは欠陥だらけで、誠に恥ずかしい教科書であふれていると言える。　超古典的な高木貞治氏の解析概論にも確かな欠陥が出てきた。勾配や曲率、ローラン展開、コーシーの平均値定理さえ進化できる。
ゼロ除算の歴史は、数学界の避けられない世界史上の汚点に成るばかりか、人類の愚かさの典型的な事実として、世界史上に記録されるだろう。この自覚によって、人類は大きく進化できるのではないだろうか。
そこで、我々は、これらの認知、真相の究明によって、数学界の汚点を解消、世界の文化への貢献を期待したい。
ゼロ除算の真相を明らかにして、基礎数学全般の修正を行い、ここから、人類への教育を進め、世界に貢献することを願っている。
ゼロ除算の発展には　世界史がかかっており、数学界の、社会への対応をも　世界史は見ていると感じられる。　恥の上塗りは世に多いが、数学界がそのような汚点を繰り返さないように願っている。
人の生きるは、真智への愛にある、すなわち、事実を知りたい、本当のことを知りたい、高級に言えば神の意志を知りたいということである。そこで、我々のゼロ除算についての考えは真実か否か、広く内外の関係者に意見を求めている。関係情報はどんどん公開している。
４周年、思えば、世の理解の遅れも反映して、大丈夫か、大丈夫かと自らに問い、ゼロ除算の発展よりも基礎に、基礎にと向かい、基礎固めに集中してきたと言える。それで、著書原案ができたことは、楽しく充実した時代であったと喜びに満ちて回想される。
以　上

再生核研究所声明 405(2017.12.31): 　ゼロ除算が拓いた幾何学の現象　―　堪らなく楽しい新奇な現象　－　デカルトの円定理から

図と式の表現が表しにくいので　簡単に参照されるサイトhttps://arxiv.org/abs/1711.04961
を挙げて　その中の図と式を参照して頂いて、ゼロ除算が如何に面白いかを解説したい。
まず、始めにデカルトの円定理と呼ばれる美しい定理を参照して下さい。3つの円が外接するときに、それらに内接したり、外接する円の半径の間の関係を確立した定理です。
式は美しいのですが、表現で４つの半径は、完全に対称になっていることに気づけばさらに　美しさを深く理解できます。
論文の発想は、そもそも、点や直線は円の特別な場合と見なせるという数学を想起して、デカルトの円定理で述べた基の３つの円を　点や直線に置き換えた場合にも成り立つかと問題にしました。　点は半径ゼロの円ですが、直線も半径ゼロの円だということはゼロ除算の結果導かれた発見です。すると、デカルトの円定理の式で、1/0 　が出てきますが、それらはゼロと解釈すれば　良いとなります。それで、２つが円で、もう一つが共通接線である場合を考えると、図１－２のようですが、きれいに成り立っていることが分かります。　この辺の定理、事実は和算の得意とする分野で、デカルトの円定理も含めて和算でも広く知られていたということです。３つの円が、点や直線になった場合をすべて考えてみて何時でも成り立てば、デカルトの円定理は　一層美しいと言えます。　あらゆる場合を考えるのですが、２つが円で、一つが点の場合、それらに接する円は存在しないようですので、その場合デカルトの円定理は成り立たないようにみえます。
そこで、点では成り立たないので、小さな円の場合を考えて、その円を点にした場合にどうなるかを考えてみました。どんな小さな円でもデカルトの円定理は成り立っていますから、その小さな円の半径がゼロに近づいた場合を　考えてみるとどうなるかと考えたくなります。
数学的に厳格に議論するために、３つの円と内接円（外接円）をきちんと方程式で書いて議論しました。　円を点にするとき、　円の表現は孤立特異点を有していて、そこでは考えられないというのが　現代数学です。　ゼロ分の式はゼロのところで考えられないからです。　例えば、定理７の円の方程式で、z = 1,-1 の場合が考えられる。そこで、意味のある図形が出てくる。　ゼロ除算算法では孤立特異点で有限確定値を与えることができますので、今まで考えられなかった特異点で考えみました。―　無限の彼方が、特異点に成る場合も多い。その結果、驚嘆すべきことが起きていることが分かりました。（この辺の記述は厳密な表現より情念に思いを入れました）。
その特異点から、点円原点と、赤い円と青い円が出て来ることが分かりました。点がこれらの３つに分かれて出てきたという実に面白い現象です。　原点の場合にはデカルトの定理が成り立ちませんが、赤い円では、何とデカルトの円定理が成り立っていることが、ゼロ除算算法での計算の結果から確認できます。　青い円は美しい状況に置かれた円ですが、それは点に近づけた円が、突然、元の２つの円に外接する、しかもちょうどそれらの円を直径にする円に変形したと解釈すると、ちょうど内接する円が　緑の円で、デカルトの定理が成り立っているという、驚嘆すべき現象です。
点に成って定理が成り立たない場面で、点が突然変異を起こして定理をそのまま成り立たせている現象が現れたと発想すると、この現象は世の一般的な現象における新規な現象として注目すべきではないでしょうか。　見かけ上成り立たない場合、そこが変形して成り立たせる世界が存在する。　―　ものは燃焼で変形する、変形以前のあるものは変形してもそのまま、引き継がれている。意味深長では　ないだろうか。―　山根現象を想起して下さい。　―　これは、運動エネルギーが一定であったものが　ある時、物質は突然消えて、物質は消えて運動エネルギーが熱エネルギーに変化する現象を表しています。
赤い円は、美しいので、その分野の有名なバーコフの円と呼ばれる円ですが、２つの円に直交していますが、点に近づいていくとき、　円は接していたのですが、出てきた円は接するのではなくて、直交でしょうか。　実に面白いことは　ゼロ除算が発見した典型的な結果として、ｙ軸の勾配はゼロ、\tan(\pi/2) =0　ですから、バーコフの円は２つの円に接しているということを述べていますから、　堪らなく楽しいと言えます。―　直交は接していると解釈できるという新発見です。　緑の円は美しく３つの円に接しています。
論文では、あらゆる場合を考えたと述べていますので、３つの円が３つの点でも、３本の直線の場合も考えて、デカルトの定理は成り立っていると述べていますので、さらに面白いです。それには、ゼロの意味を考えてゼロとは何かを発見する必要が有ります。
以　上　　


再生核研究所声明 278(2016.01.27)： 面白いゼロ除算の混乱と話題

Googleサイトなどを参照すると　ゼロ除算の話題は　膨大であり、世にも珍しい現象と言える(division by zero: 約298 000 000結果（0.51秒）
検索結果
https://en.wikipedia.org/wiki/ Division_by_zero
数学では、ゼロ除算は、除数（分母）がゼロである部門です。このような部門が正式に配当である/ 0をエスプレッソすることができます(2016.1.19.13:45)).

問題の由来は、西暦６２８年インドでゼロが記録され、四則演算が考えられて、１３００年余、ゼロでは割れない、ゼロで割ることを考えてはいけないは　１０００年を超える世界史の常識であり、天才オイラーは　それは、1/0は無限であるとの論文を書き、無限遠点は　複素解析学における１００年を超える定説、確立した学問である。割り算を掛け算の逆と考えれば、ゼロ除算が不可能であることは　数学的に簡単に証明されてしまう。しかしながら、アリストテレスの世界観、ゼロの概念、無とか、真空の概念での不可思議さゆえに２０００年を超えて、議論され、そのため、ゼロ除算は　神秘的な話題　を提供させてきた。
確定した数学に対していろいろな存念が湧き、話題が絶えないことは　誠に奇妙なことと考えられる。ゼロ除算には　何か問題があるのだろうか。
先ず、多くの人の素朴な疑問は、加減乗除において、ただひとつの例外、ゼロで割ってはいけないが、奇妙に見えることではないだろうか。例外に気を惹くは　何でもそうであると言える。しかしながら、より広範に湧く疑問は、物理の基本法則である、ニュートンの万有引力の法則，アインシュタインの特殊相対性理論に　ゼロ除算が公式に現れていて、このような数学の常識が、物理的に解釈できないジレンマを深く内蔵してきた。実際、ゼロ除算の歴史は　ニュートンやアインシュタインを悩ましてきたと考えられる。
ニュートンの万有引力の法則においては　２つの質点が重なった場合の扱いであるが、アインシュタインの特殊相対性理論においては　ローレンツ因子　にゼロになる項があるからである。
特にこの点では、深刻な矛盾、問題を抱えていた。
特殊相対性理論では、光速の速さで運動しているものの質量はゼロであるが、光速に近い速さで運動するものの質量（エネルギー）が無限に発散しているのに、ニュートリノ素粒子などが、光速に極めて近い速度で運動しているにも拘わらず　小さな質量、エネルギーを有しているという矛盾である。それゆえにブラックホール等の議論とともに話題を賑わしてきている。最近でも特殊相対性理論とゼロ除算、計算機科学や論理の観点でゼロ除算が学術的に議論されている。次のような極めて重要な言葉が残されている：
George Gamow (1904-1968) Russian-born American　nuclear physicist and cosmologist remarked that "it is well known to students of high school algebra" that division　by zero is not valid; and Einstein admitted it as the biggest blunder of his life [1]：
1. Gamow, G., My World Line (Viking, New York). p 44, 1970

スマートフォン等で、具体的な数字をゼロで割れば、答えがまちまち、いろいろなジョーク入りの答えが出てくるのも興味深い。しかし、計算機がゼロ除算にあって、実際的な障害が起きた：

ヨークタウン (ミサイル巡洋艦)ヨークタウン(USS Yorktown, DDG-48/CG-48)は、アメリカ海軍のミサイル巡洋艦。タイコンデロガ級ミサイル巡洋艦の2番艦。艦名はアメリカ独立戦争のヨークタウンの戦いにちなみ、その名を持つ艦としては5隻目。
艦歴[編集]
1997年9月21日バージニア州ケープ・チャールズ沿岸を航行中に、乗組員がデータベースフィールドに0を入力したために艦に搭載されていたRemote Data Base Managerでゼロ除算エラーが発生し、ネットワーク上の全てのマシンのダウンを引き起こし2時間30分にわたって航行不能に陥った。 これは搭載されていたWindows NT 4.0そのものではなくアプリケーションによって引き起こされたものだったが、オペレーティングシステムの選択への批判が続いた。[1]
2004年12月3日に退役した。
出典・脚注[編集]
1.     ^ Slabodkin, Gregory (1998年7月13日). “Software glitches leave Navy Smart Ship dead in the water”. Government Computer News. 2009年6月18日閲覧。
　これはゼロ除算が不可能であるから、計算機がゼロ除算にあうと、ゼロ除算の誤差動で重大な事故につながりかねないことを実証している。それでゼロ除算回避の数学を考えている研究者もいる。論理や計算機構造を追求して、代数構造を検討したり、新しい数を導入して、新しい数体系を提案している。

確立している数学について話題が尽きないのは、思えば、ゼロ除算について、何か本質的な問題があるのだろうかと考えられる。　火のないところに煙は立たないという諺がある。　ゼロ除算は不可能であると　考えるか、無限遠点の概念、無限か　と考えるのが　数百年間を超える数学の定説であると言える。
ところがその定説が、　思いがけない形で、完全に覆り、ゼロ除算は何時でも可能で、ゼロで割れば何時でもゼロになるという美しい結果が　２０１４．２．２ 発見された。　結果は３篇の論文に既に出版され、日本数会でも発表され、大きな２つの国際会議でも報告されている。　ゼロ除算の詳しい解説も次で行っている：
○ 堪らなく楽しい数学-ゼロで割ることを考える(18)
数学基礎学力研究会のホームページ
URLは

また、再生核研究所声明の中でもいろいろ解説している。


以　上

Impact of ‘Division by Zero’ in Einstein’s Static Universe and Newton’s Equations in Classical Mechanics. Ajay Sharma physicsajay@yahoo.com Community Science Centre. Post Box 107 Directorate of Education Shimla 171001 India



Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.

私は数学を信じない。　アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。
1423793753.460.341866474681。

Einstein's Only Mistake: Division by Zero


ゼロ除算は定義が問題です：

再生核研究所声明　１４８（2014.2.12）　100/0=0,  0/0=0　－　割り算の考えを自然に拡張すると　―　神の意志 https://blogs.yahoo.co.jp/kbdmm360/69056435.html

再生核研究所声明１７１（2014.7.30）掛け算の意味と割り算の意味　―　ゼロ除算100/0=0は自明である？http://reproducingkernel.blogspot.jp/2014/07/201473010000.html


Title page of Leonhard Euler, Vollständige Anleitung zur Algebra, Vol. 1 (edition of 1771, first published in 1770), and p. 34 from Article 83, where Euler explains why a number divided by zero gives infinity.

私は数学を信じない。　アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。1423793753.460.341866474681。

Einstein's Only Mistake: Division by Zero

#divide by zero

TOP DEFINITION
  
A super-smart math teacher that teaches at HTHS and can divide by zero.
Hey look, that genius’s IQ is over 9000!
by Lawlbags! October 21, 2009


Dividing by zero is the biggest epic fail known to mankind. It is a proven fact that a succesful division by zero will constitute in the implosion of the universe.
You are dividing by zero there, Johnny. Captain Kirk is not impressed.

Divide by zero?!?!! OMG!!! Epic failzorz

3
  
Divide by zero is undefined.
Divide by zero is undefined.
by JaWo October 28, 2006

1) The number one ingredient for a catastrophic event in which the universe enfolds and collapses on itself and life as we know it ceases to exist.

2) A mathematical equation such as a/0 whereas a is some number and 0 is the divisor. Look it up on Wikipedia or something. Pretty confusing shit.

3) A reason for an error in programming
Hey, I divided by zero! ...Oh shi-

a/0

Run-time error: '11': Division by zero
by DefectiveProduct September 08, 2006

When even math shows you that not everything can be figured out with math. When you divide by zero, math kicks you in the shins and says "yeah, there's kind of an answer, but it ain't just some number."

It's when mathematicians become philosophers.
Math:
Let's say you have ZERO apples, and THREE people. How many apples does each person get? ZERO, cause there were no apples to begin with

Not-math because of dividing by zero:
Let's say there are THREE apples, and ZERO people. How many apples does each person get? Friggin... How the Fruitcock should I know! How can you figure out how many apples each person gets if there's no people to get them?!? You'd think it'd be infinity, but not really. It could almost be any number, cause you could be like "each person gets 400 apples" which would be true, because all the people did get 400 apples, because there were no people. So all the people also got 42 apples, and a million and 7 apples. But it's still wrong.
by Zacharrie February 15, 2010
投稿者 時刻:

0 件のコメント:

コメントを投稿

登録: コメントの投稿 (Atom)