再生核研究所: Division by zero is undefined is a lie (maybe)

2015年6月6日土曜日

Division by zero is undefined is a lie (maybe)

定義されていないゼロ除算は嘘です（多分）

Goodlookinguyによって11月13、2012に投稿されました

アップデート

私はゼルダの間のライブダイアログ論争にこれを回した（チームのページに見える）とI.

私は私が行ってしまった後に、多かれ少なかれ、私はゼロの結論と、任意の数以上（または以下）、非存在VS存在の問題だからゼロが相互作用することはできませんになってきたことことに注意したいと思います。

アップデート2

わかりましたので、私は少しそれを変更しました。存在から不存在を作成することができますが、非存在が存在を作成することはできません。これは、1-1 = 0によって証明されています。1-0 = 1; 1 + 0 = 1; 円はと0-0 = 0（、以下のビットを説明します）。0 + 0 = 0。

私は誰かが元の投稿を読んで、非常に私の議論を理解していないと確信していますので、私は、このアップデートで若干異なり、それを紹介します。

あなたはリンゴを選択しようとしている人です。私はあなたが現在ゼロリンゴを運んでいることを主張するつもりです。これは、あなたが何を保持していないことを意味します。そこで開催される事は非存在です。あなたはリンゴを選択するときは、ゼロから追加されていません。あなたは1りんごの塩基番号で始まる実際にあります。その前に、何のりんごはありませんでした。これはあなたが何もなかったことを意味します。それがすべてで、何もなかったように、それはあまりゼロりんごではありませんでした。それはあなたが実際にあなたがりんごのn個の数を持っていたと言うことができ、その最初のリンゴまでではなかったです。

すべての負の数は、あなた負の数が存在するが自分自身をだましている告げる誰でも0です。あなたはリンゴから正の数を削除することができますが、あなたが持つことができるりんごの最低数は、リンゴや何の存在しない値で終わることができ、すなわち0です。

5りんごそれぞれ0リンゴの木を考えると、あなたは0りんごを取得します。非存在の存在を作成することができないためです。あなたが存在していない何かに存在するものを掛ける場合は、非存在、すなわち0の値を取得します。

0で割った5りんごを考えると、あなたは上述したように、これは0を取得し、存在と非存在が対話することができません。5は何で割ることができないので、その後の答えは0です。人々は、これは未定義を指していなければならないと思うかもしれないです。これは間違っています。これは、未定義を指していません。これは、数学者は、それらの間の相互作用を強制することを決めたまで数学で相互作用しない0存在と非存在を指します。

5/1 = 5。1 * 5 = 5; 5/5 = 1; < - これは、一般的にPIEまたはEIRなどのエレクトロニクス分野で使用される三つの基であり、

我々は存在と非存在と対話しようとすると何が起こるかを見ます

5/0 =？; ？* 0 = 5; 5 /？= 0

それは我々が得るものです。我々は不可能値を取得します。おそらく存在しない値。それは未定義ではありません。それは0/0について、何の0言えばある、不可能であるため、存在しないのですか？

0/0 = 0、1。0 * 0 = 0。0/0 = 0、1。

0/0を考えると私は非存在のもののみを複数の非存在と非存在を返しますので0 0を返します。で割ったものがばかりの存在のような複数の非存在と相互作用することができることを証明することができる唯一の存在と相互作用することができます。

アップデート3

さて、私はちょうど自然な重ね合わせの存在を証明したと思います。私はそれに応じて最後の更新を更新しました。

0/1 = 0を考えます。1 * 0 = 0。我々はその後、同時に= 0 0/0および1ことを証明することができます。

ある意味で、これはまた、宇宙の証拠を提供します。何から何も1に等しくすることはできませんが、また0はつまり、拡張、崩壊、及び破壊のブラックホールを通って、創造のホワイトホールから新しい宇宙の再膨張です。

私はあきらめることに注意したいと思います。これは私が私の数学的経験を考慮追いつくことはあまりにも複雑です。これは小さくはないが、いずれかの素晴らしいではありません。必要に応じてコメント、私は応答しないことがあります。私は、私はこれで終わりだと思います。

オリジナルポスト

私は最近、「ゼロ除算ゼロが定義されていないのはなぜ/不定」と呼ばれるカーンアカデミーでこのビデオの上を見ました。私が撮影した数学のクラス、私がやった自己勉強し、私が長年行ってきたプログラミングから、私は通常、ゼロで割ったものが定義されていないことに同意します。しかし、私は私がこの回答との強い問題を取ることができ、その種類のダニが私を通過していました。主な問題は、私は考え、答えは0が何かであることを示唆しているという事実です。未定義が間違っているところです。0は何もありません。それはそれだけで何もない、未定義ではありません。

あなたは5（すなわち0/5）の0パンケーキを持っている場合は、まだ何のパンケーキを持っていません。それはあなたが何もない、と言うことです。何によってパンケーキを分割に同じロジックを適用します。何も存在しないではないので、答えは、同様です。0は何で割ったものではありません0自身を含む0で割ったものの唯一の成果です。あなたが持っていないと何もしないものを分けることはできません。ああおよびヒト型の説明では、0人の方に行く5パンケーキを想像してみてください。各存在しない人はどのように多くのパンケーキを得るのですか？明らかに0。にパンケーキを与えるために誰もありません。あなたがそこには誰もいませんので、誰にパンケーキのいずれかを与えることはできません。それは0です。

未定義さゼロで割ったもののこの奇妙な信念は愚かです。提示引数は、彼らがゼロになるように両方の方向に正と負の数の方が大きいと大きく成長して示しています。この引数は、それだけで間違った方法であると考えています、間違っていません。あなたが参照して、提示引数は除算を存在しないものがある場合は、数は逆符号で大きくなることを言います。何が越えることができないと、0が存在しないという事実です。それは除外です。他の人が存在しないが、ゼロでは存在しません。したがって、数は任意の方向に成長していない、それは単に0です。

私は誰かがこれを読んで一緒に来て、論争に変換します願っています。http://www.nrgs.org/1711/division-by-zero-is-undefined-is-a-lie/

お知らせ179：ゼロによる除算は、z / 0 = 0として明確であり、それは数学の基本であります

\ documentclass [12ptの] {}記事

\ USEPACKAGE {latexsym、amsmath、amssymb、amsfonts、amstext、amsthm}

\ numberwithin {式} {セクション}

\ {文書}を開始

\タイトルは{\ bfのお知らせ179：ゼロによる除算は、z / 0 = 0として明確であり、それは数学の基本である\\

}

\著者カーネルを再生する{{\ it研究所} \\

\日付{\今日}

\ maketitle

{\抽象BF：}この発表では、ゼロ除算$ Z / 0 = 0 $を導入しなければなりません。結果は明確な一つであり、それは数学の基本です。

\ bigskip

\セクション{はじめに}

％の\ラベル{SECT1}

画分の自然な拡張によって

\ {式}を開始

\ FRAC {B} {A}

\エンド{式}

$と$ B $を$任意の複素数のために、我々は、最近では、任意の複素数の$ B $のために、驚くべき結果を見つけました

\ {式}を開始

\ FRAC {B} {0} = 0、

\エンド{式}

ちなみに\で行列のアダマール積反転用チホノフ正則によって{S}引用し、我々は彼らの特性を議論し、実数の場合の\の一般的画分に{kmsy}をいくつかの物理的解釈を引用しました。結果は\で、一般的な分数関数は{CS}を引用するための非常に特殊なケースです。　

ゼロ除算は、しかし、AD 628のインドのゼロの文書以来の物理的な視点で（ゼロ除算で、例えば、グーグルのサイトを参照してください）世界中の長い不思議な物語を持っています、

罪-EI、高橋（\引用{タカ}）（も参照\引用{kmsyは}）の画分のいくつかの完全な拡張機能を解析することにより、およびプロパティ（1.2）のための完全な特性を示すことによって、シンプルで決定的な解釈（1.2）を設立しました。彼の結果は、私たちの数学の結果（1.2）は、天然ものとして受け入れられるべきであると述べていることが表示されます：

\ bigskip

{\のBFの命題。} $ {\のBFのC}となるように$回は{\ bfののC} $ \ {\それはFが$ {\ BFをCから関数とします}

F（b、a）のF（C、D）= F（BC、AD）

すべてのための

{\のBFのC}でA、B、C、Dの\

と

F（B、A）= \ FRAC {B} {A}、\クワッド、{\のBFのC}のB \、\ね0。

そこで、{\のBFのC} $の任意の$ bは\のために、取得します

F（B、0）= 0。

}

\ medskip

\セクション{$ / B $留分とは何ですか？}

多くの数学者のために、分割$ bは/ $、製品の逆数として考慮されます。

すなわち、画分であります

\ {式}を開始

\ FRAC {B} {A}

\エンド{式}

方程式の解として定義されます。

\ {式}を開始

X = Bの\ CDOT。

\エンド{式}

アイデアと式（2.2）は、強力な結論で、ゼロ除算が不可能であることを示しています。一方、問題が長く、古い質問されています：

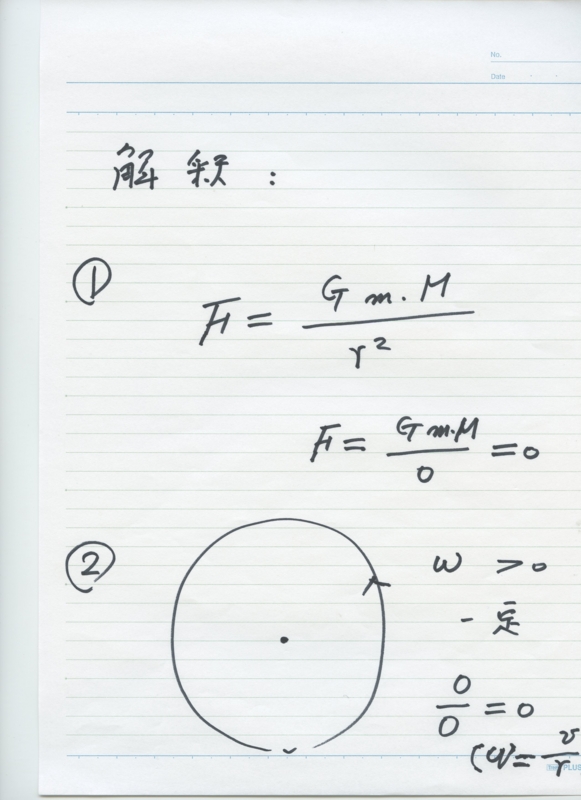
ゼロ除算の典型的な例として、ニュートンによって基本法を想起しなければなりません。

\ {式}を開始

F = G \ FRAC {M_1 M_2} {R ^ 2}

\エンド{式}

2つの塊のための$ M_1、M_2 $距離の$のR $とし、一定の$ G $に対する。もちろん、

\ {式}を開始

\ lim_ {0するには、r \} F = \ inftyの、

\エンド{式}

しかし、私たちの分画中

\ {式}を開始

F = G \ FRAC {M_1のM_2} {0} = 0。

\エンド{式}

\ medskip

今、私たちは別のアプローチを紹介しなければなりません。分割の$ B / $が{\ BF独立製品の}定義することができます。実際、日本、分割$ bの/ $で。$ bは、$ {\のBFのraruは} $（{\ bfの城山を}）$ $ $ $ bは$に存在するどのように多くのように定義され、このアイデアは、減算$繰り返し$から来ています。（一方で、製品がほかから来ています）。

「分裂」のための日本語では、独立して、製品のような概念が存在します。

H. Michiwakiと彼の6歳の少女が、結果は、独立した画分、製品のコンセプトの意味から、明らかであると彼らは言った100ドル/ 0 = 0 $という結果のために言いました：

100ドル/ 0 = 0 $ 100ドル= 0 \回0 $という意味ではありません。一方、多くの数学者は結果のための混乱がありました。

彼女の理解は妥当であると許容できます。

100ドル/ 2 = 50 \クワッド$はその後、それぞれが50を持つことになり、私たちは2で100を分割することを意味します。

$ 10分の100 = 10 \クワッド$はその後、それぞれが10を持つことになり、私たちは100 by10を分割することを意味します。

クワッド$ \ $ 100/0 = 0は、我々は100を分割せず、その後、誰もがすべてので、0にしていないことを意味します。

また、彼女はその後、残りは100です。これは数学的に、です。

100 = 0の\ CDOT 0 + 100。

今、すべての数学者は些細なものとして自然な感情とゼロ100ドル/ 0 = 0 $で除算を受け入れることができますか？

\ medskip

簡単にするために、我々は非負の実数の数値を考慮しなければなりません。我々は、しかし、我々はゼロ除算のための世話をする必要があり、分割（または分数）$ bの/その計算のための通常の手順に従って、$を定義したいです：

次のように100ドル/ 2、例えば、第1の原則は、$我々はそれを考慮しなければなりません：

100-2-2-2 - 、...、 - 2。

どのように時間が我々は、$ 2 $を引くことができますすることができますか？この場合で、それは50回であり、したがって、画分は50 $ $です。

次のように第二の場合は、たとえば、$ 3月2日$のために我々はそれを考慮しなければなりません：

3から2 = 1

残り（残り）は、当社の複数の$ 10 $、残りのための$ 1 $ $ 1 $であり、

次のように我々は、同様に考慮してください。

10-2-2-2-2-2 = 0。

そのため10ドル/ 2 = 5 $と私たちは次のように定義します。

\ FRAC {3} {2} = 1 + 0.5 = 1.5。

これらの手順では、$ \ね0 $のために我々は通常、分数の$ B / $を定義することができます。ここでは、製品のコンセプトを必要としません。ゼロ除算を除いて、画分のすべての結果が有効であり、受け入れられています。

今、私たちは、例えば、100ドル/ 0 $をゼロ除算を考慮しなければなりません。から

100から0 = 100、

つまり、減算100ドル - 0 $、100は低下しないので、我々は、我々は100ドル$から任意のものを引くと言うことはできません。したがって、減算数をゼロとして理解されるべきです。すなわち、

\ FRAC {100} {0} = 0。

私たちはこのことを理解することができます：$ 0 $で除算し、それが100ドル$を分割しないので、結果が0 $ $であることを意味します。

同様に、我々はそれを見ることができます

\ FRAC {0} {0} = 0。

結論として、我々は、任意の$ bは$のために、ゼロとしてdivisonを定義する必要があります

\ FRAC {B} {0} = 0。

\詳細については、{} kmsy引用を参照してください。

\ medskip

{複雑な分析では} \セクション

そこで我々は、（1.2）のように、任意の複素数の$ B $のために、考慮すべきです。

それは、マッピングのために、あります

\ {式}を開始

W = \ FRAC {1} {Z}、

\エンド{式}

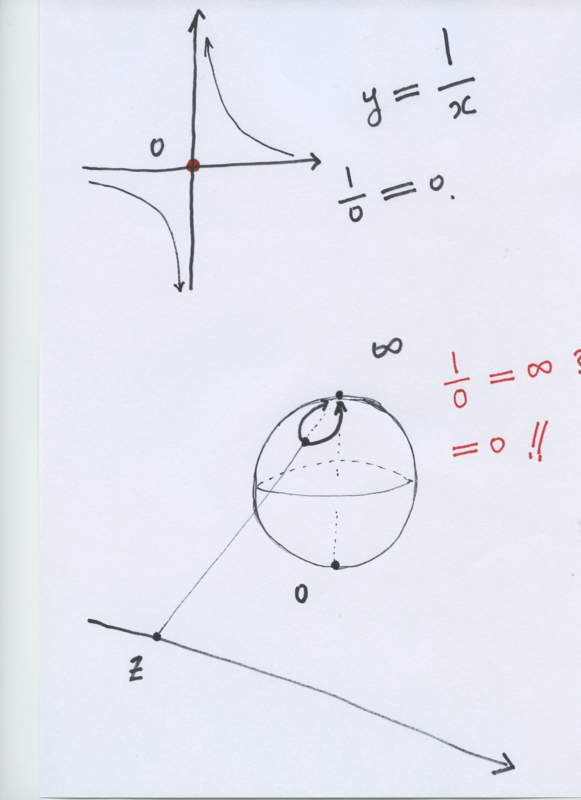
$ Z = 0 $の画像は、= 0 $ W $です。この事実は、リーマン球面上の無限遠点のための私達の十分に確立された一般的なイメージと関連して好奇心の一つであると思われます。

しかし、我々は、初等関数を呼び出ししなければなりません

\ {式}を開始

FRAC {1} {Z} \ W（Z）= \ EXP

\エンド{式}

= 1 + \ FRAC {1} {1！Z} + \ FRAC {1} {2！Z ^ 2} + \ FRAC {1} {3！Z ^ 3} + \ CDOT \ CDOT \ CDOT。

関数は原点を中心に本質的な特異点を持っています。我々は（1.2）を考えると、一方、驚くべきことに、我々が持っています：

\ {式}を開始

W（0）= 1。

\エンド{式}

{\無限遠点が数値ではありません、BF}と私たちはゼロ点の$ Z = 0 $で関数（3.2）を検討することができなくなり、一方、我々は（3.3）のように値が$ 1 $を考慮することができますゼロ点の$ Z = 0 $で。どのように我々は、これらの状況を考慮していますか？

LV Ahlforsは（\ {ahlfors}を引用）のような周知の数とリーマン球面モデルとして無限遠点を紹介しました複素解析で有名な標準的な教科書では、しかし、私たちの解釈は番号として適切であろう。我々は、数として無限遠点を受け入れることができなくなります。

典型的な結果として、我々は驚くべき結果を導き出すことができます。この結果、拡張のための重要なアプリケーションとしては、{。自然な意味を持つの\ BF} {\それを解析関数の孤立特異点で、それは一定の値をとります}分析的パラメータを持つ関数の式を得ることができ、単一の積分はゼロ除算でinterpretatedすることができる、自然に（\ {msty}を引用）。

\ bigskip

\セクション{まとめ}

ゼロの$ B / 0 = 0 $で除算が可能であり、結果は自然に一意に決定されます。

結果から、本数学と矛盾しない - しかし、複雑な分析で、我々はポールのために少しプレゼンテーションを変更する必要があります。ない、本質的に、私たちは基本的に、ゼロ除算を考慮していなかったため。

ゼロ除算は不可能である共通の理解は、多くの教科書と数理科学の本で変更する必要があります。画分の定義があっても、小学校{Michiwakiの方法、それを\}によって導入することができます。

我々は広く、美しい事実を教えるべき？：

基本的な機能の基本グラフの

Y = F（X）= \ FRAC {1} {X}、

F（0）= 0。

結果は、広く適用可能であり、宇宙（{\ BFを発表166}）のための新たな理解が得られます。

\ medskip

ゼロの$ B / 0 = 0 $での除算が導入されていない場合、それは数学が意味で不完全であることをようで、ゼロ除算のintoductionにより、数学は意味で、完全かつ完璧に美しくなります。