四一郎さんの「0で割る話」 何か面白くて、残しておきたくなったのでまとめました。 （２４番外）を読んで、自分は「いろいろ知っていない」人間なのだなあと（＾＾； 0って奥が深くて怖いっすね。

四一郎さんの「0で割る話」

何か面白くて、残しておきたくなったのでまとめました。

（２４番外）を読んで、自分は「いろいろ知っていない」人間なのだなあと（＾＾；

0って奥が深くて怖いっすね。

k3akinori 24790 view 267 コメント 529 68 91 お気に入り

100

まとめメニュー

四一郎 @yon_ichiro 2012-11-27 23:45:13

（１）さて、数日前TL上で話題になった「０で割る話」、について少々書いてみます。この問題はずっと昔からあると思っています。そして、純粋に算数・数学の枠に収まる問題ではないようにも感じています。

四一郎 @yon_ichiro 2012-11-27 23:47:04

（２）まずは私の妻の体験談から。小学生のころ、やはり先生に「２÷０は０だ」と言われたのだそうです。そこで妻は反論します。「２÷１＝２、２÷０．１＝２０、２÷０．０１＝２００、２÷０．００１＝２０００、……と、割る数が０に近づくにつれて割り算の結果は大きくなっていく、」（続く）

四一郎 @yon_ichiro 2012-11-27 23:48:33

（３）「なのに２÷０がいきなり０ではおかしいと思う。」あとでも述べますが、演算の連続性を欲すれば当然こういう考えになりますし、実際、演算の連続性は欲しいです。で、その先生の答えが「でも、０だと決まっているんだ。」もうどこからどう突っ込んでいいかわかりませんが。

四一郎 @yon_ichiro 2012-11-27 23:51:10

（４）妻にこの話を聞いたのは10年くらい前ですが、それから私は気にし続けていて、折りあるごとに中学生や高校生に、小学校で「０で割ること」をどう教わったかを訊いています。結果は「割れないと言われた」「０だと言われた」「そんな話は聞いたことがない」「忘れた」が拮抗しています。

四一郎 @yon_ichiro 2012-11-27 23:53:50

（５）で、長年いろいろな人に話を聞いているうちに、私はこの「０で割る話」には、純粋な数学的誤解のほかに、学校空間での教員と児童の関係の問題と、「答えがない」「考えない」と言うことに対する誤解がある、という考えになってきました。

四一郎 @yon_ichiro 2012-11-27 23:56:54

（６）学校空間での教員と児童（生徒）の関係性については、誰しも一家言ありますよね。ここでは省略。そういえば小6のころに「カンペキってのは壁のようにきれいで整っていることです」と先生に言われ、『故事成語事典』を読んだばかりの四一郎少年は戦いましたが、もちろん負けました。

四一郎 @yon_ichiro 2012-11-27 23:59:15

（７）で、次の「答えがない」「考えない」ということに対する誤解の話。いきなりですが、詰将棋というパズルがあります。互いに最善を尽くした場合、たった一通りだけ一方が勝ちになる手順がある、それを見つけよ、そして、それが確かに勝ちであることと、それ以外に勝ち手順がないことを（続く）

四一郎 @yon_ichiro 2012-11-28 00:00:54

（８）証明せよ、というパズルで、何百年も前からすばらしい作品が多数作られています。で、そんな中にも、パズルとして成立していないもの、失敗作がどうしてもあるわけですが、その一つが「不詰」、一方が勝ちになる手順がまったく存在しない、という場合です。

四一郎 @yon_ichiro 2012-11-28 00:03:57

（９）「不詰」というのは、一方がどんなに手段を尽くしても、他方に正しく応対されると勝てない、ということですが、この証明はなかなか厄介です。人間業とは思えないような妙防があったりするからで、これを発見しないと「不詰」の証明はできない。でも、そこはがんばって証明するわけです。

四一郎 @yon_ichiro 2012-11-28 00:05:57

（１０）で、その「不詰」の証明がされた詰将棋、に対して「でも詰む手順があるかもしれないじゃん」とか「がんばりが足りないんじゃないの？」とか言うのっておかしいですよね。あるいは「でも銀が横に行けたら詰む」とかも変ですよね。しかし、これと似たことが数学に対して言われることがあります。

四一郎 @yon_ichiro 2012-11-28 00:07:48

（１１）これは本当は「０で割る話」とはちょっと違うんですが、関連性から先に話しますが、数学には「…することは不可能である」というタイプの定理がいくつもあります。有名なのは「定規とコンパスだけでは角の三等分はできない」とか「5次以上の方程式に解の公式は存在しない」とか。

四一郎 @yon_ichiro 2012-11-28 00:11:24

（１１番外）気がさすので、さっきの命題を正確に。「定規とコンパスを、作図のルールに従って用いるのみでは、一般に与えられた角を三等分することはできない」、「加減乗除と累乗根演算のみを許す限り、n≧5のときは、複素係数ｎ次方程式に対し、一般的な解の公式は存在しない」

四一郎 @yon_ichiro 2012-11-28 00:13:25

（１２）で、このタイプの定理を説明すると、…いや私自身はそういう目にあったことはなくて伝聞なんですが…「いつかできるかもしれないじゃないか」「それはがんばりが足らないんだ、あきらめてどうする！」「定規とコンパス以外の器具を使えば、ほらできるよ！」みたいなことが言われるのです。

四一郎 @yon_ichiro 2012-11-28 00:15:32

（１３）数学でいう「できない」とは、「これまで誰も成功したことがない」という意味ではありません。「どんな手段を尽くしてもできない、ということを論理的に証明した」ということです。まさに、詰将棋の「不詰」の証明と同じことです。「できない」はあきらめているのではなくて、（続く）

四一郎 @yon_ichiro 2012-11-28 00:18:54

（１４）極めて積極的で誇りに満ちた主張なのです。だから、（１２）みたいなことを言われるのは完全にお門違い（でもそうはっきり言うといろいろ怒られるのでやんわりと）（でもそんなの無理だけどー）。野崎昭弘先生の名著『不完全性定理』は、不可能を証明しうる人間の叡智への賛歌でもあります。

四一郎 @yon_ichiro 2012-11-28 00:24:40

（１５）さて、やっと「０で割る話」に戻ります。数学的見地から言うと、この話の答えは「割り算 a÷b は、b=0 のときは、定義しない」ということになります。この、『定義しない』てのもわかりにくいんだろうなあ。『考えない』ということもあるんですが余計わかりにくいのかもしれない。

四一郎 @yon_ichiro 2012-11-28 00:27:10

（１６）ひらたくいえば、「０で割るということは数学の理論体系の中ではやりません」、もっと思い切って言えば「０で割ってはいけません」ということ。しかし、禁止されるとムカつきますよね。どうして、って訊きたくなりますよね。……その理由はあとにしまして、（つづく）

四一郎 @yon_ichiro 2012-11-28 00:29:46

（１７）この「０で割った答えを決めない」「０で割った答えと言うものはない」というのが、誤解を招いていると思うんです。「決めないって、決めればいいじゃん」「答えがないって、問題なんだから答えはあるはずだろ」「もしかして答え知らないんじゃない？」など、現場ではきっといろいろあるはず。

四一郎 @yon_ichiro 2012-11-28 00:32:50

（１８）あとで述べますが、数学で「０で割った答えを定義しない」ことには、理論全体を考慮した積極的な理由があるのです。しかしそれをよくわかっていないために、自信を持って「定めない」と言えなかったり、「あるはず」と勝手に思い込んでいる「答え」を「０」ということにしてしまうのでは、と。

四一郎 @yon_ichiro 2012-11-28 00:36:19

（１９）「答えがない」ということを主張するのが大変だ、ということは、さっき言った「不詰の詰将棋」を「不詰」だと主張することの大変さ、と同じだと思います。詰まなさそう、ではだめで、すべての手順を読み切って断言しなければならない。それなりに勉強しなければできないことです。

四一郎 @yon_ichiro 2012-11-28 00:38:05

（２０）もっとも、「０で割ることは定義しない」ことの数学的理由はそんなに難しくありません。これはすでにあちこちで言われているとおりです。一口に割り算と言っても、3つくらいの意味がありますが、どこから考えても「０で割った結果ってのは決めようがないなあ」と初等的に思えます。

四一郎 @yon_ichiro 2012-11-28 00:39:33

（２１）「あ」２÷０とは、２kgの小麦粉を０人で等分する、ということです。しかし、なにしろ０人ですからねえ。「１人あたりの小麦粉の量」っていうのがないですね。ですから、２÷０は定められません。

四一郎 @yon_ichiro 2012-11-28 00:41:08

（２２）「い」２÷０とは、２ｋｇの小麦粉を０ｋｇずつの小袋に小分けする、ということです。それでいくつ袋が必要か、ということですが、なにしろ０ｋｇですから、いくら袋を用意しても２ｋｇの小麦粉がなくなる日は絶対にやってきません。ですから、２÷０は定められません。

四一郎 @yon_ichiro 2012-11-28 00:42:55

（２３）「う」２÷０とは、「０を何倍したら２になりますか？」というクイズの答えです。しかし、０って何と掛け合わせても０が答えになるんですよね。２には決してなりません。つまり、２÷０の答えとして資格を持つ数は、存在しません。

四一郎 @yon_ichiro 2012-11-28 00:45:22

（２４）ところで、この話をややこしくする要因の一つに「無限」とか「無限大」とか言われるものがあります。２÷０＝無限大、みたいな。しかし、これは「無限大などという数はない」「無限大という概念が存在するとしても、それは数といえるものではない」というのが答えになります。

四一郎 @yon_ichiro 2012-11-28 00:49:19

（24番外）「いや、実数体を一点コンパクト化して……」とか「複素数全体に無限遠点を付け加えて球面だと思って……」とか言い出す人は、ちゃんといろいろ知っている人なので、同業者の手品を生暖かく見ている手品師のような気持ちになって、にやにやしながら黙っていましょうね。

四一郎 @yon_ichiro 2012-11-28 00:53:31

（25）2÷0の値（数としての）を無理に定義すると、どうやったところで、数学の理論体系を傷めてしまいます。「単位量あたりの量を求める」という割り算本来の意味が損なわれますし、0×aが0でない可能性を認めることにより、分配法則や符号反転数（加法逆元）の存在も怪しくなります。

四一郎 @yon_ichiro 2012-11-28 00:56:18

（26）つまり、２÷０の値を定めないのは、面倒だとか逃げてるとかそういうのではなくて、数学という学問を作り上げるためにぜひとも必要だからそうしているのです。冒頭紹介した妻の指摘もそう、2÷a=b のとき、a の値の変動が小さければ b の値の変動も小さい、ということが（続く）

四一郎 @yon_ichiro 2012-11-28 00:58:13

（27）保障されていなければ、いろいろやりにくくてしかたがない。それを数学の言葉では「（複素数体での）除法は連続である」とか「（複素数体は）位相体である」とかいいますが、まあ、自然な要求だと思います。妻の追及を「決まっているから」で片付けた先生は、残念ながら学問者とはいえない。

四一郎 @yon_ichiro 2012-11-28 01:00:08

（27番外）誤解されるかもしれないので一応。「２÷a=bで、aの値の変動が小さければbの値の変動も小さい」は横着な言い方で、正しくは、「…bの値の変動を小さくせよと要求されたときに、それがどんな厳しい要求であっても、aの値の変動を十分小さくすれば、要求にこたえられる」です。

四一郎 @yon_ichiro 2012-11-28 01:01:29

ええと、いろいろ書いているうちに自分でも何を言って何を言っていないか混乱してくるんだよな……大画面パソコンほしいな……。

四一郎 @yon_ichiro 2012-11-28 01:07:21

（２８）まとめると、現在私が「０で割る話」について考えることは次のようになるかな。０で割るという演算を定義しないことには学問的理由が厳然存在する。しかし、それはそれなりに学んでわかることであり（といっても、先生と言われるからには学んでいてほしいけれど、まあそこはいろいろあるから）

四一郎 @yon_ichiro 2012-11-28 01:09:46

（２９）加えて「定義しない」「答えがない」ということに関する不慣れ・不信感もあり、「０で割った答えはない」と主張することにためらいを感じる人もいるだろう。それがもしも小学校の教員であり、しかも……ええ、なんというか……ある種、弱い心と強い行動のセットを持っている場合、

四一郎 @yon_ichiro 2012-11-28 01:12:26

（30）とりあえず手近にある数である「０」を、「０で割った答え」として児童に押し付けてしまうこともあるだろう。こういうことになります。だから対策は、「数学をみんな勉強しましょう」だけではなく、「『知らない』や『間違う』をもっとみんなで共有して認め合う社会を」ってのもあるような。

四一郎 @yon_ichiro 2012-11-28 01:13:16

（31）どっちにせよ、数学者、というか、数学という学問に関わる者たちががんばらないといけないのは確かですね。どう、がんばればいいのか、それがなかなか難しいんですが。

四一郎 @yon_ichiro 2012-11-28 01:15:06

（32）あ、あとね、一つ言い忘れていたんだけれど、「０で割る話には触れない」という態度も学校空間ではあるらしいんですね。ややこしいから避ける、ということなんだろうけど、これは危険でよくないと思う。子どもたちには好奇心がある。ほかの数では行える割り算が、０で割る話だけ（続く）

四一郎 @yon_ichiro 2012-11-28 01:16:56

（33）説明されない、すると絶対、自分たちで考えようとしますよね。そのとき、自分たちで正しい結論を得られればいいけど、それにはこの話はちょっと難しいでしょう。そこで数学を知っている大人や、よい数学の本（これはたくさんあります！）に出会えればいいですけど……それもねえ。

四一郎 @yon_ichiro 2012-11-28 01:19:40

（34・終）うーん、全部言い切った感じもしないし、うまく言えていないような気もするのですが、今日のところはひとまずこんなところでしょうか。このところ連続ツイートしたい内容が続き、結果みなさんのTLをお騒がせしてしまい、すみませんでした……。ありがとうございました！

http://togetter.com/li/414222

再生核研究所声明２２２（2015.4.8）日本の代表的な数学として　　ゼロ除算の研究の推進を求める

ゼロ除算の成果は　２０１５．３．２３　明治大学で開催された日本数学会で（プログラムは５２００部印刷、インターネットで公開）、海外約２００名に経過と成果の発表を予告して　正規に公開された。簡単な解説記事も約２００部学会で配布された。インターネットを用いて１年以上も広く国際的に議論していて、骨格の論文も出版後１年以上も経過していることもあり、成果と経過は一応の諒解が広く得られたと考えても良いと判断される。経過などについては　次の一連の声明を参照：

再生核研究所声明148（2014.2.12）　100/0=0, 0/0=0　－　割り算の考えを自然に拡張すると　―　神の意志

再生核研究所声明154（2014.4.22）　新しい世界、ゼロで割る、奇妙な世界、考え方

再生核研究所声明157（2014.5.8）　知りたい　神の意志、ゼロで割る、どうして　無限遠点と原点が一致しているのか？

再生核研究所声明161（2014.5.30）　ゼロ除算から学ぶ、数学の精神　と　真理の追究

再生核研究所声明163（2014.6.17）　ゼロで割る（零除算）－　堪らなく楽しい数学、探そう零除算　―　愛好サークルの提案

再生核研究所声明166（2014.6.20）　ゼロで割る（ゼロ除算）から学ぶ　世界観

再生核研究所声明171（2014.7.30）　掛け算の意味と割り算の意味　―　ゼロ除算100/0=0は自明である？

再生核研究所声明176（2014.8.9）　ゼロ除算について、数学教育の変更を提案する

Announcement 179 (2014.8.25): Division by zero is clear as z/0=0 and it is fundamental in mathematics

Announcement 185　: The importance of the division by zero $z/0=0$

再生核研究所声明188（2014.12.1５）　ゼロで割る（ゼロ除算）から観えてきた世界

再生核研究所声明190（2014.12.24）

再生核研究所からの贈り物　―　ゼロ除算100/0=0,　0/0=0

再生核研究所声明192（2014.12.27）　無限遠点から観る、人生、世界

夜明け、新世界、再生核研究所　年頭声明

―　再生核研究所声明193（2015.1.1）―　

再生核研究所声明194（2015.1.2）　大きなイプシロン（無限小）、創造性の不思議

再生核研究所声明195（2015.1.3）　ゼロ除算に於ける高橋の一意性定理について

再生核研究所声明196（2015.1.4）　ゼロ除算に於ける山根の解釈100= 0ｘ0について

再生核研究所声明200（2015.1.16）　ゼロ除算と複素解析の現状　―佐藤超関数論との関係が鍵か？

再生核研究所声明202（2015.2.2）　ゼロ除算100/0=0,0/0=0誕生1周年記念声明　―　ゼロ除算の現状と期待

再生核研究所声明215（2015.3.11）　ゼロ除算の教え

日本の数学が、欧米先進国のレベルに達していることは、国際研究環境の実情を見ても広く認められる。しかしながら、初等教育から大学学部レベルの基本的な数学において　日本の貢献は　残念ながら特に見当たらないと言わざるを得ない。これは日本の数学が　大衆レベルでは　世界に貢献していないことを意味する。これについて　関孝和の微積分や行列式の発見が想起されるが、世界の数学史に具体的な影響、貢献ができなかったこともあって　関孝和の天才的な業績は　残念ながら国際的に認知されているとは言えない。

そこで、基本的なゼロ除算、すなわち、四則演算において　ゼロで割れないとされてきたことが、何でもゼロで割れば　ゼロであるとの基本的な結果は、世界の数学界における　日本の数学の顕著なものとして　世界に定着させる　良い題材ではないだろうか。

内容の焦点としてはまず：

ゼロ除算の発見、

道脇方式によるゼロ除算の意味付け、除算の定義、

高橋のゼロ除算の一意性、

衝突における山根の現象の解釈、

の４点が挙げられる。

６歳の道脇愛羽さんが、ゼロ除算は　除算の固有の意味から自明であると述べられていることからも分かるように、ゼロ除算は、ピタゴラスの定理を超えた基本的な結果であると考えられる。

ゼロ除算の研究の発展は　日本の代表的な数学である　佐藤の超関数の理論と密接な関係にあり（再生核研究所声明200）、他方、欧米では　Aristotélēs　の世界観、universe　は連続である　との偏見に陥っている現状がある。　最後にゼロ除算の意義　に述べられているように　ゼロ除算の研究は　日本の数学として発展させる絶好の分野であると考えられる。　そこで、広く関係者に研究の推進と結果の重要性についての理解と協力を求めたい。

ゼロ除算の意義：

１）西暦６２８年インドでゼロが記録されて以来　ゼロで割るの問題　に　簡明で、決定的な解　1/0=0, 0/0=0をもたらしたこと。

２）　ゼロ除算の導入で、四則演算　加減乗除において　ゼロでは　割れない　の例外から、例外なく四則演算が可能である　という　美しい四則演算の構造が確立されたこと。

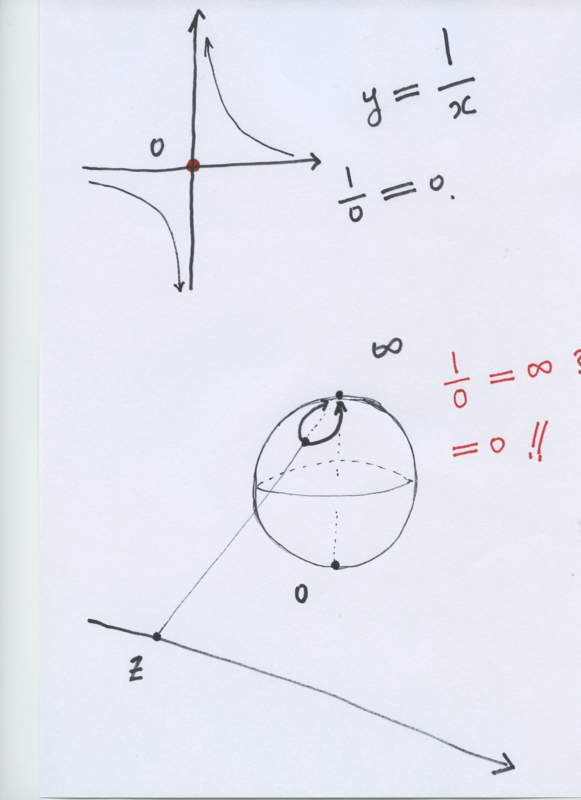
３）２千年以上前に　ユークリッドによって確立した、平面の概念に対して、おおよそ２００年前に非ユークリッド幾何学が出現し、特に楕円型非ユークリッド幾何学ではユークリッド平面に対して、無限遠点の概念がうまれ、特に立体射影で、原点上に球をおけば、　原点ゼロが　南極に、無限遠点が　北極に対応する点として　複素解析学では　１００年以上も定説とされてきた。それが、無限遠点は　数では、無限ではなくて、実はゼロが対応するという驚嘆すべき世界観をもたらした。

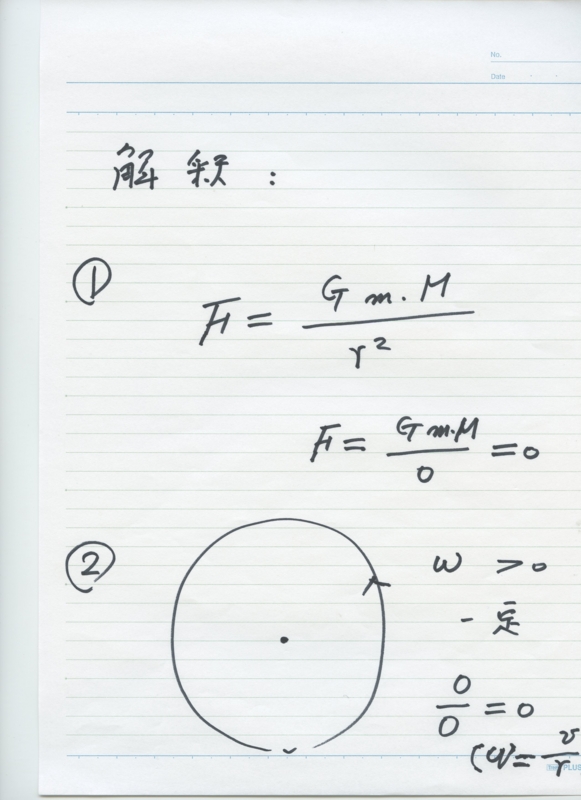
４）ゼロ除算は　ニュートンの万有引力の法則における、２点間の距離がゼロの場合における新しい解釈、　独楽（コマ）の中心における角速度の不連続性の解釈、衝突などの不連続性を説明する数学になっている。ゼロ除算は　アインシュタインの理論でも重要な問題になっていたとされている。数多く存在する物理法則を記述する方程式にゼロ除算が現れているが、それらに新解釈を与える道が拓かれた。

５）複素解析学では、１次変換の美しい性質が、ゼロ除算の導入によって、任意の１次変換は　全複素平面を全複素平面に１対１　onto　に写すという美しい性質に変わるが、　極である１点において不連続性が現れ、ゼロ除算は、無限を　数から排除する数学になっている。

６）ゼロ除算は、不可能であるという立場であったから、ゼロで割る事を　本質的に考えてこなかったので、ゼロ除算で、分母がゼロである場合も考えるという、未知の新世界、新数学、研究課題が出現した。

７）複素解析学への影響は　未知の分野で、専門家の分野になるが、解析関数の孤立特異点での性質について新しいことが導かれる。典型的な定理は、どんな解析関数の孤立特異点でも、解析関数は　孤立特異点で、有限な確定値をとる　である。佐藤の超関数の理論などへの応用がある。

８）特異積分におけるアダマールの有限部分や、コーシーの主値積分は、弾性体やクラック、破壊理論など広い世界で、自然現象を記述するのに用いられている。面白いのは　積分が、もともと有限部分と発散部分に分けられ、　極限は　無限たす、有限量の形になっていて、積分は　実は、普通の積分ではなく、そこに現れる有限量を便宜的に表わしている。ところが、その有限量が実は、　ゼロ除算にいう、　解析関数の孤立特異点での　確定値に成っていること。いわゆる、主値に対する解釈を与えている。これはゼロ除算の結果が、広く、自然現象を記述していることを示している。

９）中学生や高校生にも十分理解できる基本的な結果をもたらした：

基本的な関数y = 1/x　のグラフは、原点で　ゼロである；すなわち、　1/0=0　である。

１０）既に述べてきたように　道脇方式は　ゼロ除算の結果100/0=0,　0/0=0および分数の定義、割り算の定義に、小学生でも理解できる新しい概念を与えている。多くの教科書、学術書を変更させる大きな影響を与える。

１１）ゼロ除算が可能であるか否かの議論について：

現在　インターネット上の情報でも　世間でも、ゼロ除算は　不可能であるとの情報が多い。それは、割り算は　掛け算の逆であるという、前提に議論しているからである。それは、そのような立場では、勿論　正しいことである。出来ないという議論では、できないから、更には考えられず、その議論は、不可能のゆえに　終わりになってしまう　―　もはや　展開の道は閉ざされている。しかるに、ゼロ除算が　可能であるとの考え方は、それでは、どのような理論が　展開できるのかの未知の分野が望めて、大いに期待できる世界が拓かれる。

１２）ゼロ除算は、数学ばかりではなく、　人生観、世界観や文化に大きな影響を与える。

次を参照：

再生核研究所声明166（2014.6.20）ゼロで割る（ゼロ除算）から学ぶ　世界観

再生核研究所声明188（2014.12.16）ゼロで割る（ゼロ除算）から観えてきた世界

ゼロ除算における新現象、驚きとは　Aristotélēs　の世界観、universe　は連続である　を否定して、強力な不連続性を　universe　の現象として受け入れることである。

以　上

まして、１０個のリンゴを０人で分けた際に、取り分　が∞個の小さな部分が取り分は、どう考えてもおかしい・・・・