Are we living in a HOLOGRAM? For the first time, scientists prove strange theory could be true in 'realistic models' of our universe
Holographic principle suggests there is a 2D surface that we can't see
This surface contains all the information needed to describe 3D objects
Since 1997, equations used to show holographic principle could be true have been based on models that contradict theories about our universe
Now scientists have shown how it works in universe that is largely flat
By ELLIE ZOLFAGHARIFARD FOR DAILYMAIL.COM
PUBLISHED: 18:57 GMT, 27 April 2015 | UPDATED: 00:42 GMT, 28 April 2015
1k
shares
323
View comments
We are living in a giant hologram, and everything we see around us is merely a projection of a two-dimensional surface.
This is the bizarre theory put forward in 1997 by physicist Juan Maldacena, who was able to prove its existence in equations that only partially explain our universe.
Now researchers in Austria have, for the first time, been able to show how this strange holographic principle can also work in a more realistic model of our cosmos.
Scroll down for video
We are living in a giant hologram, and everything we see around us is a projection of a 2D surface. This is the bizarre theory put forward in 1997 by Juan Maldacena. Now researchers in Austria have, for the first time, been able to show how this strange holographic principle can work in a realistic model of our cosmos
- 2
We are living in a giant hologram, and everything we see around us is a projection of a 2D surface. This is the bizarre theory put forward in 1997 by Juan Maldacena. Now researchers in Austria have, for the first time, been able to show how this strange holographic principle can work in a realistic model of our cosmos
THE HOLOGRAPHIC PRINCIPLE
The holographic principle claims gravity in the universe comes from thin, vibrating strings.
These strings are holograms of events that take place in a simpler, flatter cosmos.
The principle suggests that, like the security chip on your credit card, there is a two-dimensional surface that contains all the information needed to describe a three-dimensional object - which in this case is our universe.
The theory claims that data containing a description of a volume of space - such as a human or a comet - could be hidden in a region of this flattened, 'real' version of the universe.
In a black hole, for instance, all the objects that ever fall into it would be entirely contained in surface fluctuations, almost like a piece of computer memory on contained in a chip.
In a larger sense, the theory suggests that the entire universe can be seen as a 'two-dimensional structure projected onto a cosmological horizon' - or in simpler terms, a projection.
If we could understand the laws that govern physics on that distant surface, the principle suggests we would grasp all there is to know about reality.
The holographic principle suggests that, like the security chip on your credit card, there is a two-dimensional surface that we can't see.
This surface contains all the information needed to describe a three-dimensional object - which in this case is our universe.
In essence, the principle claims that data containing a description of 3D object – such as the device you're reading this on - could be hidden in a region of this flattened, 'real' version of the universe.
Maldacena came to this conclusion when he discovered that mathematical descriptions of the universe actually require one fewer dimension than it seems.
But up until now, this principle has only been studied in something known as 'curved anti-de-sitter spaces' – or exotic spaces with negative curvature.
Scientists came up with these spaces as way to combine describing gravity in a three-dimensional setting while predicting quantum particles in two spatial dimensions.
Anti-de-sitter spaces are negatively curved, and any object thrown away on a straight line will eventually return.
The problem is they are very different from the spaces in our own universe.
Our universe is largely flat, and on astronomic distances, it has positive curvature.
The latest study by scientists at the Technology University of Vienna now suggests that the holographic principle holds in a flat space-time.
'Juan Maldacena proposed the idea that there is a correspondence between gravitational theories in curved anti-de-sitter spaces on the one hand and quantum field theories in spaces with one fewer dimension on the other', says Daniel Grumiller from the Technology University of Vienna.
RELATED ARTICLES
Previous
1
Next
Decoding the beauty of orchids: Experts discover the...
Has the Easter Island 'hat' mystery been solved? Red...
Lasers reveal what taste LOOKS like: Live imaging of the...
Take a flying tour of Vesta: Interactive 3D map reveals...
SHARE THIS ARTICLE
Share
1k shares
To test the theory, scientists spent three years creating gravitational equations that do not require exotic spaces and, instead, live in a flat space.
'If quantum gravity in a flat space allows for a holographic description by a standard quantum theory, then there must by physical quantities, which can be calculated in both theories – and the results must agree', says Grumiller.
Daniel Grumiller's 'New force at large distances' TEDx Talk
The holographic principle suggests that, like the security chip on your credit card, there is a two-dimensional surface that we can't see. This surface contains all the information needed to describe a three-dimensional object - which in this case is our universe
- 2
The holographic principle suggests that, like the security chip on your credit card, there is a two-dimensional surface that we can't see. This surface contains all the information needed to describe a three-dimensional object - which in this case is our universe
They said one key feature of quantum mechanics –quantum entanglement – had to appear in the more realistic model of our universe.
When quantum particles are entangled, they cannot be described individually.
They form a single quantum object, even if they are located far apart.
There is a measure for the amount of entanglement in a quantum system, called 'entropy of entanglement'.
The team showed that this entanglement takes the same value in both a flat quantum gravity model and in a low dimension quantum field theory.
'This calculation affirms our assumption that the holographic principle can also be realised in flat spaces,' said Max Riegler at the Technology University of Vienna.
'It is evidence for the validity of this correspondence in our universe', says Max Riegler (TU Wien).
'The fact that we can even talk about quantum information and entropy of entanglement in a theory of gravity is astounding in itself, and would hardly have been imaginable only a few years back,' added Grumiller.
'That we are now able to use this as a tool to test the validity of the holographic principle, and that this test works out, is quite remarkable.'
Read more:
TEDx Talks - YouTube
Follow us: @MailOnline on Twitter | DailyMail on Facebookhttp://www.dailymail.co.uk/sciencetech/article-3057957/Are-living-HOLOGRAM-time-scientists-prove-strange-theory-true-realistic-models-universe.html
Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 179: Division by zero is clear as z/0=0 and it is fundamental in mathematics\\
}
\author{{\it Institute of Reproducing Kernels}\\
Kawauchi-cho, 5-1648-16,\\
Kiryu 376-0041, Japan\\
E-mail: kbdmm360@yahoo.co.jp\\
}
\date{\today}
\maketitle
{\bf Abstract: } In this announcement, we shall introduce the zero division $z/0=0$. The result is a definite one and it is fundamental in mathematics.
\bigskip
\section{Introduction}
%\label{sect1}
By a natural extension of the fractions
\begin{equation}
\frac{b}{a}
\end{equation}
for any complex numbers $a$ and $b$, we, recently, found the surprising result, for any complex number $b$
\begin{equation}
\frac{b}{0}=0,
\end{equation}
incidentally in \cite{s} by the Tikhonov regularization for the Hadamard product inversions for matrices, and we discussed their properties and gave several physical interpretations on the general fractions in \cite{kmsy} for the case of real numbers. The result is a very special case for general fractional functions in \cite{cs}.
The division by zero has a long and mysterious story over the world (see, for example, google site with division by zero) with its physical viewpoints since the document of zero in India on AD 628, however,
Sin-Ei, Takahasi (\cite{taka}) (see also \cite{kmsy}) established a simple and decisive interpretation (1.2) by analyzing some full extensions of fractions and by showing the complete characterization for the property (1.2). His result will show that our mathematics says that the result (1.2) should be accepted as a natural one:
\bigskip
{\bf Proposition. }{\it Let F be a function from ${\bf C }\times {\bf C }$ to ${\bf C }$ such that
$$
F (b, a)F (c, d)= F (bc, ad)
$$
for all
$$
a, b, c, d \in {\bf C }
$$
and
$$
F (b, a) = \frac {b}{a }, \quad a, b \in {\bf C }, a \ne 0.
$$
Then, we obtain, for any $b \in {\bf C } $
$$
F (b, 0) = 0.
$$
}
\medskip
\section{What are the fractions $ b/a$?}
For many mathematicians, the division $b/a$ will be considered as the inverse of product;
that is, the fraction
\begin{equation}
\frac{b}{a}
\end{equation}
is defined as the solution of the equation
\begin{equation}
a\cdot x= b.
\end{equation}
The idea and the equation (2.2) show that the division by zero is impossible, with a strong conclusion. Meanwhile, the problem has been a long and old question:
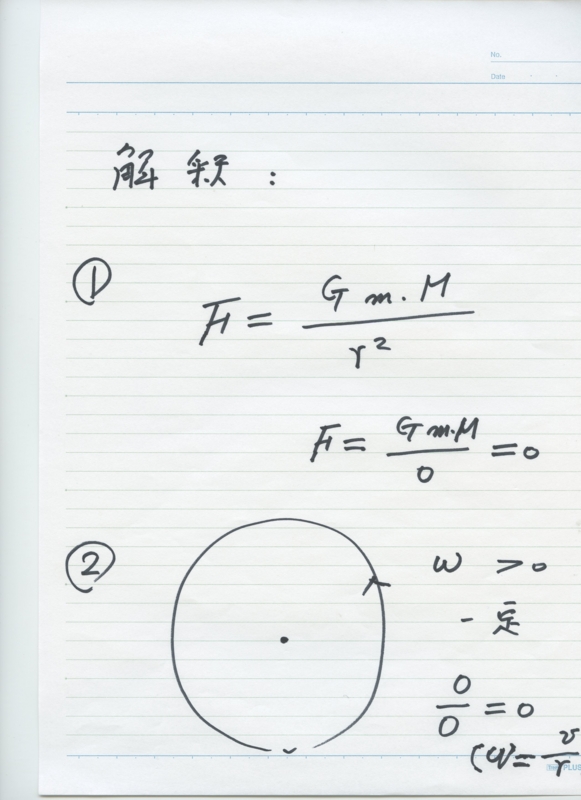
As a typical example of the division by zero, we shall recall the fundamental law by Newton:
\begin{equation}
F = G \frac{m_1 m_2}{r^2}
\end{equation}
for two masses $m_1, m_2$ with a distance $r$ and for a constant $G$. Of course,
\begin{equation}
\lim_{r \to +0} F =\infty,
\end{equation}
however, in our fraction
\begin{equation}
F = G \frac{m_1 m_2}{0} = 0.
\end{equation}
\medskip
Now, we shall introduce an another approach. The division $b/a$ may be defined {\bf independently of the product}. Indeed, in Japan, the division $b/a$ ; $b$ {\bf raru} $a$ ({\bf jozan}) is defined as how many $a$ exists in $b$, this idea comes from subtraction $a$ repeatedly. (Meanwhile, product comes from addition).
In Japanese language for "division", there exists such a concept independently of product.
H. Michiwaki and his 6 years old girl said for the result $ 100/0=0$ that the result is clear, from the meaning of the fractions independently the concept of product and they said:
$100/0=0$ does not mean that $100= 0 \times 0$. Meanwhile, many mathematicians had a confusion for the result.
Her understanding is reasonable and may be acceptable:
$100/2=50 \quad$ will mean that we divide 100 by 2, then each will have 50.
$100/10=10 \quad$ will mean that we divide 100 by10, then each will have 10.
$100/0=0 \quad$ will mean that we do not divide 100, and then nobody will have at all and so 0.
Furthermore, she said then the rest is 100; that is, mathematically;
$$
100 = 0\cdot 0 + 100.
$$
Now, all the mathematicians may accept the division by zero $100/0=0$ with natural feelings as a trivial one?
\medskip
For simplicity, we shall consider the numbers on non-negative real numbers. We wish to define the division (or fraction) $b/a$ following the usual procedure for its calculation, however, we have to take care for the division by zero:
The first principle, for example, for $100/2 $ we shall consider it as follows:
$$
100-2-2-2-,...,-2.
$$
How may times can we subtract $2$? At this case, it is 50 times and so, the fraction is $50$.
The second case, for example, for $3/2$ we shall consider it as follows:
$$
3 - 2 = 1
$$
and the rest (remainder) is $1$, and for the rest $1$, we multiple $10$,
then we consider similarly as follows:
$$
10-2-2-2-2-2=0.
$$
Therefore $10/2=5$ and so we define as follows:
$$
\frac{3}{2} =1 + 0.5 = 1.5.
$$
By these procedures, for $a \ne 0$ we can define the fraction $b/a$, usually. Here we do not need the concept of product. Except the zero division, all the results for fractions are valid and accepted.
Now, we shall consider the zero division, for example, $100/0$. Since
$$
100 - 0 = 100,
$$
that is, by the subtraction $100 - 0$, 100 does not decrease, so we can not say we subtract any from $100$. Therefore, the subtract number should be understood as zero; that is,
$$
\frac{100}{0} = 0.
$$
We can understand this: the division by $0$ means that it does not divide $100$ and so, the result is $0$.
Similarly, we can see that
$$
\frac{0}{0} =0.
$$
As a conclusion, we should define the zero divison as, for any $b$
$$
\frac{b}{0} =0.
$$
See \cite{kmsy} for the details.
\medskip
\section{In complex analysis}
We thus should consider, for any complex number $b$, as (1.2);
that is, for the mapping
\begin{equation}
w = \frac{1}{z},
\end{equation}
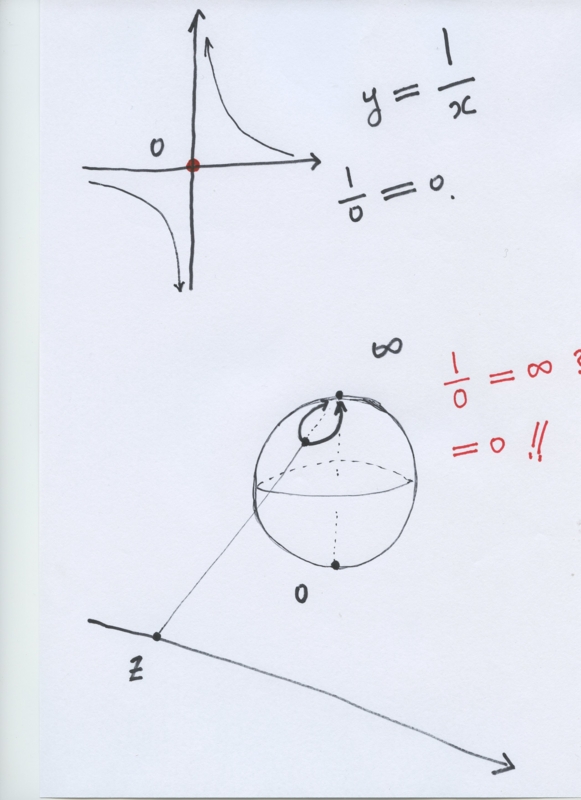
the image of $z=0$ is $w=0$. This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere.
However, we shall recall the elementary function
\begin{equation}
W(z) = \exp \frac{1}{z}
\end{equation}
$$
= 1 + \frac{1}{1! z} + \frac{1}{2! z^2} + \frac{1}{3! z^3} + \cdot \cdot \cdot .
$$
The function has an essential singularity around the origin. When we consider (1.2), meanwhile, surprisingly enough, we have:
\begin{equation}
W(0) = 1.
\end{equation}
{\bf The point at infinity is not a number} and so we will not be able to consider the function (3.2) at the zero point $z = 0$, meanwhile, we can consider the value $1$ as in (3.3) at the zero point $z = 0$. How do we consider these situations?
In the famous standard textbook on Complex Analysis, L. V. Ahlfors (\cite{ahlfors}) introduced the point at infinity as a number and the Riemann sphere model as well known, however, our interpretation will be suitable as a number. We will not be able to accept the point at infinity as a number.
As a typical result, we can derive the surprising result: {\it At an isolated singular point of an analytic function, it takes a definite value }{\bf with a natural meaning.} As the important applications for this result, the extension formula of functions with analytic parameters may be obtained and singular integrals may be interpretated with the division by zero, naturally (\cite{msty}).
\bigskip
\section{Conclusion}
The division by zero $b/0=0$ is possible and the result is naturally determined, uniquely.
The result does not contradict with the present mathematics - however, in complex analysis, we need only to change a little presentation for the pole; not essentially, because we did not consider the division by zero, essentially.
The common understanding that the division by zero is impossible should be changed with many text books and mathematical science books. The definition of the fractions may be introduced by {\it the method of Michiwaki} in the elementary school, even.
Should we teach the beautiful fact, widely?:
For the elementary graph of the fundamental function
$$
y = f(x) = \frac{1}{x},
$$
$$
f(0) = 0.
$$
The result is applicable widely and will give a new understanding for the universe ({\bf Announcement 166}).
\medskip
If the division by zero $b/0=0$ is not introduced, then it seems that mathematics is incomplete in a sense, and by the intoduction of the division by zero, mathematics will become complete in a sense and perfectly beautiful.
\bigskip
section{Remarks}
For the procedure of the developing of the division by zero and for some general ideas on the division by zero, we presented the following announcements in Japanese:
\medskip
{\bf Announcement 148} (2014.2.12): $100/0=0, 0/0=0$ -- by a natural extension of fractions -- A wish of the God
\medskip
{\bf Announcement 154} (2014.4.22): A new world: division by zero, a curious world, a new idea
\medskip
{\bf Announcement 157} (2014.5.8): We wish to know the idea of the God for the division by zero; why the infinity and zero point are coincident?
\medskip
{\bf Announcement 161} (2014.5.30): Learning from the division by zero, sprits of mathematics and of looking for the truth
\medskip
{\bf Announcement 163} (2014.6.17): The division by zero, an extremely pleasant mathematics - shall we look for the pleasant division by zero: a proposal for a fun club looking for the division by zero.
\medskip
{\bf Announcement 166} (2014.6.29): New general ideas for the universe from the viewpoint of the division by zero
\medskip
{\bf Announcement 171} (2014.7.30): The meanings of product and division -- The division by zero is trivial from the own sense of the division independently of the concept of product
\medskip
{\bf Announcement 176} (2014.8.9): Should be changed the education of the division by zero
\bigskip
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{ahlfors}
L. V. Ahlfors, Complex Analysis, McGraw-Hill Book Company, 1966.
\bibitem{cs}
L. P. Castro and S.Saitoh, Fractional functions and their representations, Complex Anal. Oper. Theory {\bf7} (2013), no. 4, 1049-1063.
\bibitem{kmsy}
S. Koshiba, H. Michiwaki, S. Saitoh and M. Yamane,
An interpretation of the division by zero z/0=0 without the concept of product
(note).
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{msty}
H. Michiwaki, S. Saitoh, M. Takagi and M. Yamada,
A new concept for the point at infinity and the division by zero z/0=0
(note).
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95.http://www.scirp.org/journal/ALAMT/
\bibitem{taka}
S.-E. Takahasi,
{On the identities $100/0=0$ and $ 0/0=0$}
(note).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operators on the real and complex fields. (submitted)
\end{thebibliography}
\end{document}
アインシュタインも解決できなかった「ゼロで割る」問題
私は数学を信じない。 アルバート・アインシュタイン / I don't believe in mathematics. Albert Einstein→ゼロ除算ができなかったからではないでしょうか。





















0 件のコメント:
コメントを投稿