Quiz on famous endings
The Hindu BusinessLine-19 時間前8 If it started at the age of four, with the Tamil film Kandhan Karunai, with what, usually associated with the ancient Indian mathematician Brahmagupta, did it end in 2018? 9 What did we see the last of with a match involving ...
https://www.thehindubusinessline.com/blink/hang/quiz-on-famous-endings/article25850331.ece
Wasan Geometry and Division by Zero Calculus
2018年11月28日(水) テーマ:数学
Sangaku Journal of Mathematics (SJM) ⃝c SJM ISSN 2534-9562 Volume 2 (2018), pp. 57-73 Received 20 November 2018. Published on-line 29 November 2018 web: http://www.sangaku-journal.eu/ ⃝c The Author(s) This article is published with open access1 . Wasan Geometry and Division by Zero Calculus
file:///C:/Users/saito%20saburo/Downloads/SJM_2018_57-73_okumura_saitoh%20(1).pdf
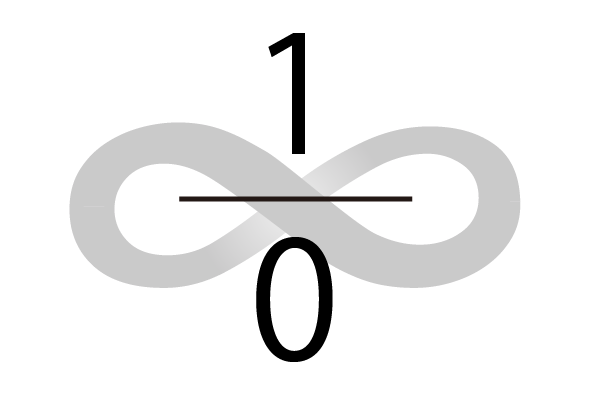
ゼロ除算の発見は日本です:
∞???
∞は定まった数ではない・・・・
人工知能はゼロ除算ができるでしょうか:
とても興味深く読みました:2014年2月2日 4周年を超えました:
ゼロ除算の発見と重要性を指摘した:日本、再生核研究所
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 461: An essence of division by zero and a new axiom}
\author{{\it Institute of Reproducing Kernels}\\
kbdmm360@yahoo.co.jp
}
\date{2018.11.10}
\maketitle
In order to see an essence of our division by zero calculus, we will state a simple survey.
As the number system, division by zero is realized as the {\bf Yamada field} with the definition of the general fractions $a/b$ containing the case $b=0$, and its various meanings and applications are given. In particular, see \cite{msy} and see also the references.
The field structure is, of course, fundamental in the algebraic structure.
However, apart from various motivations and any background, we will give the definition of the division by zero calculus as follows:
\medskip
For any \index{Laurent expansion}Laurent expansion around $z=a$,
\begin{equation} \label{dvc5.1}
f(z) = \sum_{n=-\infty}^{-1} C_n (z - a)^n + C_0 + \sum_{n=1}^{\infty} C_n (z - a)^n
\end{equation}
we define the division by zero calculus
\begin{equation}\label{dvc5.2}
f(a) = C_0.
\end{equation}
For the correspondence \eqref{dvc5.2} for the function $f(z)$, we will call it {\bf the division by zero calculus}. By considering derivatives in \eqref{dvc5.1}, we {\bf define} any order derivatives of the function $f$ at the singular point $a$ as
$$
f^{(n)}(a) = n! C_n.
$$
\medskip
The division by zero calculus seems to be strange firstly, however, by its various applications and results, we will see that the concept is fundamental in our elementary mathematics, globally. See the references.
For its importance, the division by zero calculus may be looked as a {\bf new axiom.}
\medskip
Firstly, for the fundamental function $W= F(z) = 1/z$, we have, surprisingly
$$
F(0) = 0.
$$
We see its great impacts to our basic idea for the space and in our Euclidean space.
From the form, we should consider that
\begin{equation}
\frac{1}{0} =0.
\end{equation}
Note that this representation and identity is not any result, but it is only the definition of
$\frac{1}{0}$. Of course, it is not the usual definition as the solution of the equation $0 \cdot z =1$. Here, we are stating that the division by zero calculus and the form of the elementary function lead us to the identity (0.3).
\medskip
\bigskip
{\bf \Large Could we divide the numbers and functions by zero?}
\medskip
For this old and general question, we will give a simple answer.
For any analytic function
$f(z)$ around the origin $z=0$ that is permitted to have any singularity at $z=0$ (of course, any constant function is permitted),
we can consider the value, by the division by zero calculus
\begin{equation}
\frac{f(z)}{z^n}
\end{equation}
at the point $z=0$, for any positive integer $n$. This will mean that from the form
we can consider it as follows:
\begin{equation}
\frac{f(z)}{z^n}\mid_{x=0}.
\end{equation}
\bigskip
For example,
$$
\frac{e^{x}}{x^n}\mid_{x=0} = \frac{1}{n!}.
$$
\medskip
{\bf \Huge In this sense, we can divide the numbers and analytic functions by zero.}
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ms16}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$,
Advances in Linear Algebra \& Matrix Theory, {\bf 6}(2016), 51-58
Published Online June 2016 in SciRes. http://www.scirp.org/journal/alamt
\\ http://dx.doi.org/10.4236/alamt.2016.62007.
\bibitem{mms18}
T. Matsuura, H. Michiwaki and S. Saitoh,
$\log 0= \log \infty =0$ and applications. Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics. {\bf 230} (2018), 293-305.
\bibitem{msy}
H. Michiwaki, S. Saitoh and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{mos}
H. Michiwaki, H. Okumura and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces,
International Journal of Mathematics and Computation, {\bf 2}8(2017); Issue 1, 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), {\bf 1}(2017), 70-77.
\bibitem{os}
H. Okumura and S. Saitoh, The Descartes circles theorem and division by zero calculus. https://arxiv.org/abs/1711.04961 (2017.11.14).
\bibitem{o}
H. Okumura, Wasan geometry with the division by 0. https://arxiv.org/abs/1711.06947 International Journal of Geometry.
\bibitem{os18april}
H. Okumura and S. Saitoh,
Harmonic Mean and Division by Zero,
Dedicated to Professor Josip Pe\v{c}ari\'{c} on the occasion of his 70th birthday, Forum Geometricorum, {\bf 18} (2018), 155—159.
\bibitem{os18}
H. Okumura and S. Saitoh,
Remarks for The Twin Circles of Archimedes in a Skewed Arbelos by H. Okumura and M. Watanabe, Forum Geometricorum, {\bf 18}(2018), 97-100.
\bibitem{os18e}
H. Okumura and S. Saitoh,
Applications of the division by zero calculus to Wasan geometry.
GLOBAL JOURNAL OF ADVANCED RESEARCH ON CLASSICAL AND MODERN GEOMETRIES” (GJARCMG), {\bf 7}(2018), 2, 44--49.
\bibitem{ps18}
S. Pinelas and S. Saitoh,
Division by zero calculus and differential equations. Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics. {\bf 230} (2018), 399-418.
\bibitem{s14}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182.
\bibitem{s17}
S. Saitoh, Mysterious Properties of the Point at Infinity, arXiv:1712.09467 [math.GM](2017.12.17).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\end{thebibliography}
\end{document}
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 460: Change the Poor Idea to the Definite Results For the Division by Zero -- For the Leading Mathematicians}
\author{{\it Institute of Reproducing Kernels}\\
kbdmm360@yahoo.co.jp
}
\date{2018.11.08}
\maketitle
The Institute of Reproducing Kernels is dealing with the theory of division by zero calculus and declares that the division by zero was discovered as $0/0=1/0=z/0=0$ in a natural sense on 2014.2.2. The result shows a new basic idea on the universe and space based on the new concept of division by zero calculus: for the function $f(z) = 1/z$
$$
f(0) = 0
$$
since Aristotelēs (BC384 - BC322) and Euclid (BC 3 Century - ), and the division by zero is since Brahmagupta (598 - 668 ?).
In particular, Brahmagupta defined as $0/0=0$ in Brāhmasphuṭasiddhānta (628), however, our world history stated that his definition $0/0=0$ is wrong over 1300 years, but, we showed that his definition is suitable.
For the details, see the site: http://okmr.yamatoblog.net/
\medskip
In the international conference:
\medskip
http://www.meetingsint.com/conferences/\\appliedphysics-mathematics\\Applied Physics and Mathematics Conference 2018\\
\medskip
\noindent
we presented the basic results on October 23 and
for the details, see the references with the talk sheets: saburousaitoh
181102.pdf :
{\Huge \bf
Close the mysterious and long history of division by zero and \\ open the new world\\ since Aristoteles-Euclid:\\ $1/0=0/0=z/0= \tan (\pi/2)=0$\\
}
and the abstract: 201810.23abstract.
\bigskip
Particularly, note that the division by zero calculus is a fundamental definition based on the basic assumption that may be considered as a new axiom for its importance.
As stated
by some physicist
\medskip
{\it Here is how I see the problem with prohibition on division by zero,
which is the biggest scandal in modern mathematics as you rightly pointed
out} (2017.10.14.08:55),
\medskip
\noindent
it seems that the long history of the division by zero is our shame and our mathematics in the elementary level has basic missings. Meanwhile, we have still great confusions and wrong ideas on the division by zero. Therefore, we would like to ask for the good corrections for the wrong ideas and some official approval for our division by zero as our basic duties.
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. {\bf 27} (2014), no 2, pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ms16}
T. Matsuura and S. Saitoh,
Matrices and division by zero $z/0=0$,
Advances in Linear Algebra \& Matrix Theory, {\bf 6}(2016), 51-58
Published Online June 2016 in SciRes. http://www.scirp.org/journal/alamt
\\ http://dx.doi.org/10.4236/alamt.2016.62007.
\bibitem{mms18}
T. Matsuura, H. Michiwaki and S. Saitoh,
$\log 0= \log \infty =0$ and applications. Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics. {\bf 230} (2018), 293-305.
\bibitem{msy}
H. Michiwaki, S. Saitoh and M.Yamada,
Reality of the division by zero $z/0=0$. IJAPM International J. of Applied Physics and Math. {\bf 6}(2015), 1--8. http://www.ijapm.org/show-63-504-1.html
\bibitem{mos}
H. Michiwaki, H. Okumura and S. Saitoh,
Division by Zero $z/0 = 0$ in Euclidean Spaces,
International Journal of Mathematics and Computation, {\bf 2}8(2017); Issue 1, 1-16.
\bibitem{osm}
H. Okumura, S. Saitoh and T. Matsuura, Relations of $0$ and $\infty$,
Journal of Technology and Social Science (JTSS), {\bf 1}(2017), 70-77.
\bibitem{os}
H. Okumura and S. Saitoh, The Descartes circles theorem and division by zero calculus. https://arxiv.org/abs/1711.04961 (2017.11.14).
\bibitem{o}
H. Okumura, Wasan geometry with the division by 0. https://arxiv.org/abs/1711.06947 International Journal of Geometry.
\bibitem{os18april}
H. Okumura and S. Saitoh,
Harmonic Mean and Division by Zero,
Dedicated to Professor Josip Pe\v{c}ari\'{c} on the occasion of his 70th birthday, Forum Geometricorum, {\bf 18} (2018), 155—159.
\bibitem{os18}
H. Okumura and S. Saitoh,
Remarks for The Twin Circles of Archimedes in a Skewed Arbelos by H. Okumura and M. Watanabe, Forum Geometricorum, {\bf 18}(2018), 97-100.
\bibitem{os18e}
H. Okumura and S. Saitoh,
Applications of the division by zero calculus to Wasan geometry.
GLOBAL JOURNAL OF ADVANCED RESEARCH ON CLASSICAL AND MODERN GEOMETRIES” (GJARCMG), {\bf 7}(2018), 2, 44--49.
\bibitem{ps18}
S. Pinelas and S. Saitoh,
Division by zero calculus and differential equations. Differential and Difference Equations with Applications. Springer Proceedings in Mathematics \& Statistics. {\bf 230} (2018), 399-418.
\bibitem{s14}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. {\bf 4} (2014), no. 2, 87--95. http://www.scirp.org/journal/ALAMT/
\bibitem{s16}
S. Saitoh, A reproducing kernel theory with some general applications,
Qian,T./Rodino,L.(eds.): Mathematical Analysis, Probability and Applications - Plenary Lectures: Isaac 2015, Macau, China, Springer Proceedings in Mathematics and Statistics, {\bf 177}(2016), 151-182.
\bibitem{s17}
S. Saitoh, Mysterious Properties of the Point at Infinity, arXiv:1712.09467 [math.GM](2017.12.17).
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operations on the real and complex fields, Tokyo Journal of Mathematics, {\bf 38}(2015), no. 2, 369-380.
\end{thebibliography}
\end{document}
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 454: The International Conference on Applied Physics and Mathematics, Tokyo, Japan, October 22-23}
\author{{\it Institute of Reproducing Kernels}\\
kbdmm360@yahoo.co.jp
}
\date{2018.9.29}
\maketitle
{\Large \bf
The Institute of Reproducing Kernels is dealing with the theory of division by zero calculus and declares that the division by zero was discovered as $0/0=1/0=z/0=0$ in a natural sense on 2014.2.2. The result shows a new basic idea on the universe and space based on the new concept of division by zero calculus: for the function $f(z) = 1/z$
$$
f(0) = 0
$$
since Aristotelēs (BC384 - BC322) and Euclid (BC 3 Century - ), and the division by zero is since Brahmagupta (598 - 668 ?).
In particular, Brahmagupta defined as $0/0=0$ in Brāhmasphuṭasiddhānta (628), however, our world history stated that his definition $0/0=0$ is wrong over 1300 years, but, we showed that his definition is suitable.
For the details, see the site: http://okmr.yamatoblog.net/
\medskip
In the above international conference:
\medskip
\medskip
John Martin, Program Coordinator\\
http://www.meetingsint.com/conferences/\\appliedphysics-mathematics\\Applied Physics and Mathematics Conference 2018\\
appliedphysics@annualmeetings.net\\
appliedphysics@meetingseries.org
\medskip
\medskip
we will present our results while 11:00-12:00, October 23 and we will accept all the related questions and comments while 13:00-15:00 around.
For the details, please see the below:
\medskip
(If a person participates in our session around the morning and afternoon free discussions, he should pay euro 250. If the person registers in a group of 5 or more, the amount will be reduced to euro 180 per person. The morning session is very valuable and has the potential to bring change in the education system.
For one night stay on 22nd October, he needs to pay euro 150.
I hope everything is clear.
Kindly let me know if any query.
Thanks!
Regards,
John)
}
\bigskip
\bigskip
{\Huge \bf
Close the mysterious and long history of division by zero and \\ open the new world since Aristoteles-Euclid: $1/0=0/0=z/0= \tan (\pi/2)=0.$
}
\bigskip
\bigskip
{\large \bf
For a triangle ABC with side length $a,b,c$.
We have the formula
$$
\frac{a^2 + b^2 - c^2}{a^2 - b^2 + c^2} = \frac{\tan B}{\tan C}.
$$
If $ a^2 + b^2 - c^2 =0$, then $C = \pi/2$. Then,
$$
0 = \frac{\tan B}{\tan \frac{\pi}{2}} = \frac{\tan B}{0}.
$$
Meanwhile, for the case
$
a^2 - b^2 + c^2 =0,
$
then $B = \pi/2$, and we have
$$
\frac{a^2 + b^2 - c^2}{0}= \frac{\tan \frac{\pi}{2}}{\tan C}=0.
$$
\end{document}















































0 件のコメント:
コメントを投稿