超弦理論（ superstring theory)

超弦理論（ superstring theory)

2015年04月01日(水)NEW !

テーマ：数学

超弦理論（ちょうげんりろん、英: superstring theory）は、物理学の理論、仮説の1つ。物質の基本的単位を、大きさが無限に小さな0次元の点粒子ではなく、1次元の拡がりをもつ弦であると考える弦理論に、超対称性という考えを加え、拡張したもの。超ひも理論、スーパーストリング理論とも呼ばれる。

宇宙の姿やその誕生のメカニズムを解き明かし、同時に原子、素粒子、クォークといった微小な物のさらにその先の世界を説明する理論の候補として、世界の先端物理学で活発に研究されている理論である。この理論は現在、理論的な矛盾を除去することには成功しているが、なお不完全な点を指摘する専門家もおり、また実験により検証することが困難であろうとみなされているため、物理学の定説となるまでには至っていない。

目次 [非表示]

1 概論

2 基本的な説明

3 宇宙論への応用

4 歴史

4.1 カルツァ＝クライン理論

4.2 弦理論初期

4.3 第1次ストリング革命

4.4 第2次ストリング革命

5 現状

5.1 問題点

6 脚注

7 参考文献

7.1 原論文

7.2 教科書

7.3 読み物

8 関連項目

8.1 関連理論

9 外部リンク

概論[編集]

超弦理論が登場する以前に最も小さなスケールを記述した理論は場の量子論である。そこでは粒子を点、すなわち点粒子として扱ってきた（局所場の理論に代わる、広がりを持った粒子の概念を導入したS行列理論や非局所場理論などもあった）。一方、超弦理論では粒子を弦の振動として表す。1960年代、イタリアの物理学者、ガブリエーレ・ヴェネツィアーノが核子の内部で働く強い力の性質をベータ関数で表し、その式の示す構造が「弦 (string)」によって記述されることに南部陽一郎、レオナルド・サスキンド、ホルガー・ベック・ニールセンらが気付いたことから始まる。

弦には「閉じた弦」と「開いた弦」の2種類を考えることができ、開いた弦はスピン1のゲージ粒子（光子、ウィークボソン、グルーオンなどに相当）を含み、閉じた弦はスピン2の重力子を含む。開いた弦の相互作用を考えるとどうしても閉じた弦、すなわち重力子を含まざるを得ない。そのため、強い力のみを記述する理論と捉えることは難しいことが分かった。

逆に言えば、弦を基本要素と考えることで、自然に重力を量子化したものが得られると考えられる。そのため、超弦理論は万物の理論となりうる可能性がある。超弦理論は素粒子の標準模型の様々な粒子を導出しうる大きな自由度を持ち、それを元に現在までに様々なモデルが提案されている。

このように極めて小さい弦を宇宙の最小基本要素と考え、自然界の全ての力を数学的に表現しようというのが、いわゆる弦理論（超弦理論、M理論を含む）の目指すところである。

この理論の想定する「ひも」の大きさが実証不可能に思えるほど小さい（プランク長程度とすると 10-35m）ことなどから、物理学の定説としての地位を得るには至っていない。また今後実証されるかどうかも未知数の理論である。

基本的な説明[編集]

一般相対性理論と量子力学の折り合いをつけた理論（量子重力理論）を構築することは、物理学者を悩ませていた大問題であった。超弦理論は、その問題を解決する可能性をもった理論である。

超弦理論には5つのバージョンがあり、それぞれタイプI、IIA、IIB、ヘテロSO(32)、ヘテロE8×E8と呼ばれる。この5つの超弦理論は理論の整合性のため10次元時空が必要である。空間の3次元に時間を加えた4次元が、我々の認識する次元数である。我々が認識できない残りの6次元は、量子レベルでコンパクト化され、小さなエネルギーでは観測できないとされる[1]。また、11次元超重力理論をその低エネルギー極限に含んだM理論は更に1次元を加えて合計11次元を必要とする[2]。これら6つの理論は様々な双対性によって互いに繋がっている[3]。超弦理論の5つのバージョンを統合するものとしてM理論が注目されている。

弦の振動は、コンパクト化されている6次元により制約を受け、その振動の形により、特定の量子を形作っている。超弦理論では基本的物体は1次元の弦であったが、M理論では加えられたもう1次元によって基本的物体は2次元の膜であると提唱されている。

また超弦理論で表記される10次元中にはDブレーンと呼ばれる様々な次元の拡がりを持ったソリトンが存在する。Dブレーンは、もともと1次元の弦が端点を持ちうる空間として定義されているものだが、重力子等の閉じた弦はこの空間に依存せずにブレーン間を往来する。

超弦理論は重力の量子論の有力な候補であり、現時点でも特殊な条件の下でならブラックホールのエントロピーに関する問題に答える事ができる。ブラックホールのエントロピーは表面積に比例しているが、この事実をDブレーンに張り付いた弦の状態を数え上げる、という方法で導き出している。これは熱力学のエントロピーを統計力学の手法で導き出すことに対応している。

宇宙論への応用[編集]

ブレーン描像を宇宙論に適用した理論は、ブレーンワールドと呼ばれ、典型的な模型では我々はこのブレーンの上に住んでいることになる。またこのモデルでは、量子力学で使われる3つの力に対して、何故重力が極端に弱いのかを説明がつけられるとしている。つまり、他の3つの力、即ち、電磁気力（電磁力ともいう）、弱い力、強い力に比較して弱いのは、他の次元にその大半が逃げてしまっているためと考えられる。

これに関連して、例えば宇宙論のインフレーションをブレーンの運動で捉えるなど、様々な研究がなされている。なお、ビッグバンは我々の存在する宇宙が所属する膜と他の膜の接触によるエネルギーが原因で起こったとするモデルもあり、エキピロティック宇宙論と呼ばれている。通常のインフレーションを導出しようとする試みも進行中である。

歴史[編集]

[icon] この節の加筆が望まれています。

カルツァ＝クライン理論[編集]

詳細は「カルツァ＝クライン理論#歴史」を参照

超弦理論は10次元時空でのみ理論が定式化されるため、超弦理論に基づいた多くのモデルでは、現実の4次元時空を導くために「カルツァ＝クライン理論」のアイデアを応用している。

1919年、テオドール・カルツァは5次元時空上での一般相対性理論（重力）を、4次元時空では、マクスウェル方程式（電磁気力）を考えるという理論の元となるアイディアをアルベルト・アインシュタインへの手紙の中で明らかにした。論文はしばらくアインシュタインの机の中にあったが、その後アインシュタインの助力を得て1921年に発表された。

1926年になって、オスカル・クラインがカルツァの理論を修正して五次元時空の理論に余剰次元を非常に小さなスケールに折りこむというコンパクト化の理論を組み込んだ理論を発展させ、カルツァ＝クライン理論として知られるようになった。

弦理論初期[編集]

詳細は「弦理論#歴史」を参照

1950年代末から1960年代にかけて強い相互作用をする粒子（ハドロン）が多く発見され、それらの分類とその構成の成り立ちについての考察が始められた。超弦理論の元となった弦理論は、こうした粒子間に働く強い力の性質を記述するために考え出された。

まず、1950年代はじめにトゥーリオ・レッジェは、ハドロンの散乱実験において、共鳴状態の静止質量の2乗とスピンとの間に直線関係があることを見出した（レッジェ軌道）。1968年にイタリアのガブリエル・ヴェネツィアーノは、レッジェ軌道を再現する非常に簡単な公式で「散乱振幅」として表現した（ヴェネツィアーノ振幅）。

その公式を元に、ハドロンは振動する弦であると発表したのが、1970年の南部陽一郎、レオナルド・サスキンド、ホルガー・ベック・ニールセンである。それぞれ独立に発表された彼らの弦理論では、ハドロンは粒子ではなく振動する弦から構成され、粒子はそれぞれの振動モードに対応するというものであった。ただしこの理論では、弦の振動に理論の不安定性を表すタキオンが含まれるという欠陥が内包されていた。

南部らの弦理論ではボース粒子のみを記述していてフェルミ粒子は扱えないという問題もあったが、当時はフェルミ粒子を含めてボース粒子以外の記述を弦理論を拡張することで解を得ようという学者は少数派であった。1971年に、フランスのP.ラモン、A.ヌヴォ、アメリカのJ.シュワルツの3人によってボース粒子とフェルミ粒子の両方が扱える模型が提唱された。この模型が、超弦理論へと発展していくことになる。

第1次ストリング革命[編集]

1984年、グリーンとジョン・シュワルツによって、10次元の超重力理論および超弦理論でアノマリーのない理論が存在することが示されると、超弦理論は脚光を浴びるようになった。 特にE8×E8のゲージ場を含むヘテロティック超弦理論において、理論の定義される10次元のうち余分な6次元をカラビ-ヤウ多様体でコンパクト化した理論は、低エネルギーで \mathcal{N}=1 の超対称性を持つ理論が導かれ、重力を含む統一理論の候補として盛んに研究された。

しかし、余分な6次元がコンパクト化されるメカニズムが不明であること、コンパクト化として可能な多様体の種類が無数にあり、その中から1つを選び出すことが摂動論の範囲では不可能であることなどの困難が存在した。

第2次ストリング革命[編集]

1995年、 ポルチンスキーによりDブレーンが超弦理論のソリトン解であることが示され、また、ウィッテンによりこれまで知られていた5つの超弦理論を統一する11次元のM理論が提唱されると、超弦理論は再び脚光を浴びることとなった。この2つは、それまでに予想されていた種々の双対性(S双対性、T双対性)と組み合わせることで、これまで摂動論の範囲でしか定義されていなかった超弦理論の非摂動的な性質の理解を深めることとなった。また、Dブレーンの低エネルギーでの性質は超対称ゲージ理論で記述されるため、ゲージ理論を用いて超弦理論の性質を調べること、逆に、Dブレーンの適当な配位を考えることでゲージ理論の非摂動的な性質を調べることが可能となり、精力的に研究された。

このDブレーンは、ブラックホールのエントロピーの表式を統計力学的に導出する際にも用いられ、超弦理論が重力の量子論であることの傍証となった。また、マルダセナによるAdS/CFT対応は、まったく別の理論である超対称ゲージ理論と超重力理論が、ある極限のもとで等価となることを予想し、超弦理論や重力理論、ゲージ理論に対して新しい知見を与えることとなった。

現状[編集]

超弦理論は、現時点では観測や実験事実を説明するまでには至っていないが、上記のようなブラックホールの問題への回答、宇宙論や現象論の模型への多大な影響、そしてホログラフィー原理の具体的な実現など、その成果を挙げるにはいとまがない。超弦理論に懐疑的な発言をしていたスティーヴン・ホーキングも、近年は超弦理論の成果を用いた研究を発表している。

一方で、Not Even Wrong[4]（邦訳：ストリング理論は科学か）[5]を執筆したPeter Woit、The Trouble With Physics（邦訳：迷走する物理学）[6]を執筆したLee Smolinのように、超弦理論は現実的に検証不能なだけでなく、物理学研究全体に有害であるとする反対派・懐疑派も存在している。

問題点[編集]

『超弦理論』では現在のところ観測されていない10次元といった多数の次元を必要とする点で問題がある。超高エネルギーでの実験が可能ならばそのような次元を直接確認し、理論を検証できる可能性があるが、21世紀初頭の技術的展望では不可能だとされている。

超対称性理論と同様に、現在観測されている素粒子の倍程度の新粒子の存在を予言する。

重力の量子論の有力候補とされているものの、現在の超弦理論は背景依存の理論形式であり、背景独立でない理論は真の量子重力理論にはなり得ないという批判がある。

カラビ-ヤウ空間の形状などに依存して、膨大な数の超弦理論が存在し得る。そのようなパラメータを調整して、我々の宇宙の物理法則と適合する超弦理論を選び出すことは計算量の面から非常に困難なことが判明している。膨大な数の超弦理論が、それぞれ別の宇宙を表すとの考え方もあるものの、我々の宇宙の法則を得られなければ、実用理論としては意味が無いかもしれない。

このため超弦理論を物理学の仮説として扱うことに疑問を持つ物理学者も多い。また弦理論の業績に対しては現在のところノーベル物理学賞は与えられていない。弦理論に重要な貢献を果たした南部陽一郎、デビッド・グロスらは別の業績で受賞している。

しかしながら、現在も探求が行われている分野でもあり、かつまた、その研究の発展は数多くの大統一理論及び、超統一理論の候補の1つとして、今も数多くの研究が行われている。http://ja.wikipedia.org/wiki/%E8%B6%85%E5%BC%A6%E7%90%86%E8%AB%96

再生核研究所声明２０２（2015.2.2）ゼロ除算100/0=0,0/0=0誕生1周年記念声明　―　ゼロ除算の現状と期待

ゼロ除算の発見、経過、解説などについては、結構な文献に記録されてきた：

再生核研究所声明148（2014.2.12）100/0=0,　0/0=0　－　割り算の考えを自然に拡張すると　―　神の意志

再生核研究所声明154（2014.4.22）新しい世界、ゼロで割る、奇妙な世界、考え方

再生核研究所声明157（2014.5.8） 知りたい　神の意志、ゼロで割る、どうして　無限遠点と原点が一致しているのか？

再生核研究所声明161（2014.5.30）ゼロ除算から学ぶ、数学の精神　と　真理の追究

再生核研究所声明163（2014.6.17）ゼロで割る（零除算）－　堪らなく楽しい数学、探そう零除算　―　愛好サークルの提案

再生核研究所声明166（2014.6.20）ゼロで割る（ゼロ除算）から学ぶ　世界観

再生核研究所声明171（2014.7.30）掛け算の意味と割り算の意味　―　ゼロ除算100/0=0は自明である？

再生核研究所声明176（2014.8.9）ゼロ除算について、数学教育の変更を提案する

Announcement 179 (2014.8.25) Division by zero is clear as z/0=0 and it is fundamental in mathematics

Announcement 185: The importance of the division by zero $z/0=0$

再生核研究所声明188（2014.12.15）ゼロで割る（ゼロ除算）から観えてきた世界

再生核研究所声明190（2014.12.24）

再生核研究所からの贈り物　―　ゼロ除算100/0=0,　0/0=0

夜明け、新世界、再生核研究所　年頭声明

―　再生核研究所声明193（2015.1.1　―　

再生核研究所声明194（2015.1.2）大きなイプシロン（無限小）、創造性の不思議

再生核研究所声明195（2015.1.3）ゼロ除算に於ける高橋の一意性定理について

再生核研究所声明196（2015.1.4）ゼロ除算に於ける山根の解釈100= 0ｘ0について

再生核研究所声明199（2015.1.15）世界の数学界のおかしな間違い、世界の初等教育から学術書まで間違っていると言える　―　ゼロ除算100/0=0,0/0=0

ゼロ除算100/0=0,0/0=0誕生1周年記念日に当たり、概観して共同研究者と共に夢を明るく　楽しく描きたい。まずは、ゼロ除算の意義を復習しておこう：

１）西暦６２８年インドでゼロが記録されて以来　ゼロで割るの問題　に　簡明で、決定的な解　ゼロで 　 何でも割れば ゼロ　 z/0=0　 である　をもたらしたこと。

２）ゼロ除算の導入で、四則演算　加減乗除において　ゼロでは　割れない　の例外から、例外なく四則演算が可能である　という　美しい四則演算の構造が確立されたこと。

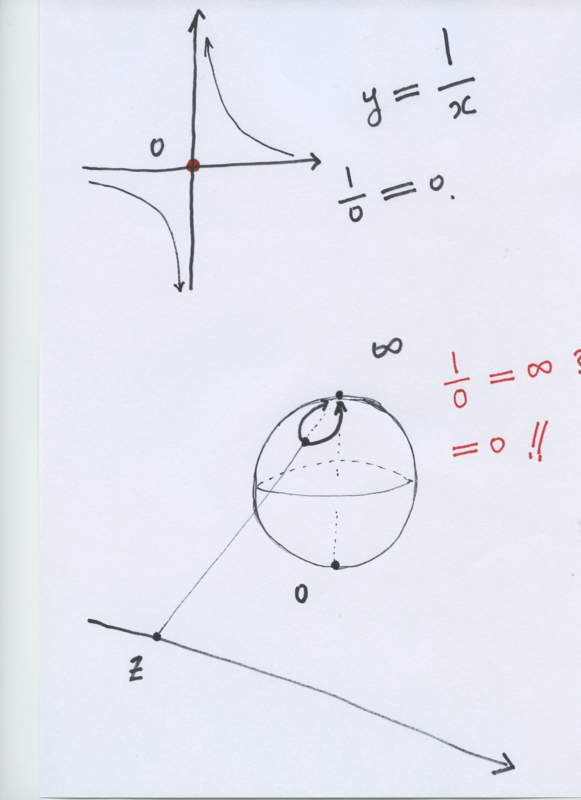
３）２千年以上前に　ユークリッドによって確立した、平面の概念に対して、おおよそ２００年前に　非ユークリッド幾何学が出現し、特に楕円型非ユークリッド幾何学ではユークリッド平面に対して、無限遠点の概念がうまれ、特に立体射影で、原点上に球をおけば、　原点ゼロが　南極に、無限遠点が　北極に対応する点として　複素解析学では　１００年以上も定説とされてきた。それが、無限遠点は　数では、無限ではなくて、実はゼロが対応するという驚嘆すべき世界観をもたらした。

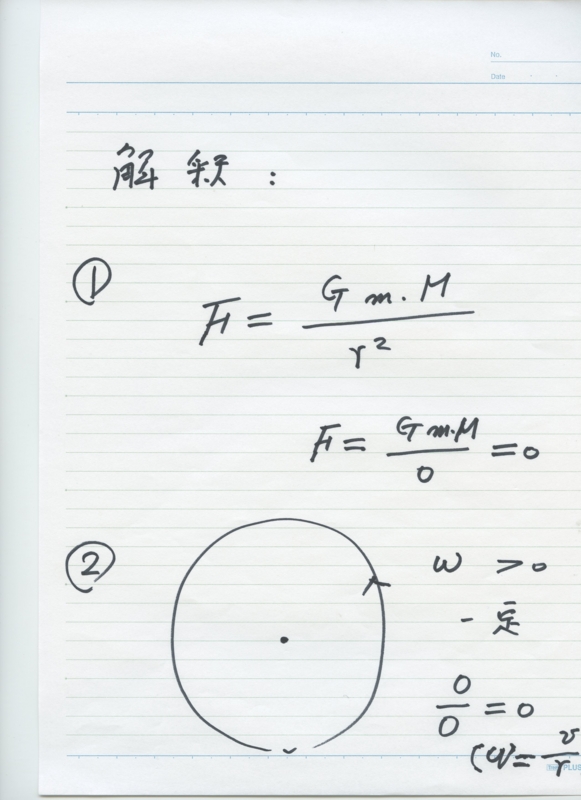
４）ゼロ除算は　ニュートンの万有引力の法則における、２点間の距離がゼロの場合における新しい解釈、独楽（コマ）の中心における角速度の不連続性の解釈、衝突などの不連続性を説明する数学になっている。ゼロ除算は　アインシュタインの理論でも重要な問題になっていたとされている。数多く存在する物理法則を記述する方程式にゼロ除算が現れているが、それらに新解釈を与える道が拓かれた。

５）複素解析学では、１次変換の美しい性質が、ゼロ除算の導入によって、任意の１次変換は　全複素平面を全複素平面に１対１　onto　に写すという美しい性質に変わるが、　極である１点において不連続性が現れ、ゼロ除算は、無限を　数から排除する数学になっている。

６）ゼロ除算は、不可能であるという立場であったから、ゼロで割る事を　本質的に考えてこなかったので、ゼロ除算で、分母がゼロである場合も考えるという、未知の新世界、新数学、研究課題が出現した。

７）複素解析学への影響は　未知の分野で、専門家の分野になるが、解析関数の孤立特異点での性質について新しいことが導かれる。典型的な結果は、どんな解析関数の孤立特異点でも、解析関数は　孤立特異点で、有限な確定値をとる　という定理　である。佐藤の超関数の理論などへの応用がある。

８）特異積分におけるアダマールの有限部分や、コーシーの主値積分は、弾性体やクラック、破壊理論など広い世界で、自然現象を記述するのに用いられている。面白いのは　積分が、もともと有限部分と発散部分に分けられ、　極限は　無限たす、有限量の形になっていて、積分は　実は、普通の積分ではなく、そこに現れる有限量を便宜的に表わしている。ところが、その有限量が実は、　ゼロ除算にいう、　解析関数の孤立特異点での　確定値に成っていること。いわゆる、主値に対する解釈を与えている。これはゼロ除算の結果が、広く、自然現象を記述していることを示している。

９）中学生や高校生にも十分理解できる基本的な結果をもたらした：

基本的な関数y = 1/x　のグラフは、原点で　ゼロである；すなわち、　1/0=0　である。

１０）既に述べてきたように　道脇方式は　ゼロ除算の結果100/0=0,　0/0=0および分数の定義、割り算の定義に、小学生でも理解できる新しい概念を与えている。多くの教科書、学術書を変更させる大きな影響を与える。

１１）ゼロ除算が可能であるか否かの議論について：

現在　インターネット上の情報でも　世間でも、ゼロ除算は　不可能であるとの情報が多い。それは、割り算は　掛け算の逆であるという、前提に議論しているからである。それは、そのような立場では、勿論　正しいことである。しかしながら、出来ないという議論では、できないから、更には考えられず、その議論は、不可能のゆえに　終わりになってしまう　―　もはや　展開の道は閉ざされている。しかるに、ゼロ除算が　可能であるとの考え方は、それでは、どのような理論が　展開できるのかという未知の分野が望めて、大いに期待できる世界が拓かれる。

１２）ゼロ除算は、数学ばかりではなく、　人生観、世界観や文化に大きな影響を与える。

次を参照：

再生核研究所声明166（2014.6.20）ゼロで割る（ゼロ除算）から学ぶ　世界観

再生核研究所声明188（2014.12.16）ゼロで割る（ゼロ除算）から観えてきた世界

ゼロ除算における新現象、驚きとは　Aristotélēs　の世界観、universe　は連続である　を否定して、強力な不連続性を　universe　の現象として表していることである。

ゼロ除算は　既に数学的に確定され、その意義も既に明らかであると考えられるが、声明１９９にも述べられているように、ゼロ除算が不可能であるとの世の常識、学術書、数学は　数学者の勝手な解釈による歴史的な間違いに当たる　ことをしっかりと理解させ、世の教育書、学術書の変更を求めていきたい。―　誰が、真実を知って、偽りを教え、言い続けられるだろうか。―　教育に於ける除算、乗算の演算の意味を　道脇方式で回復させ、新しい結果　ゼロ除算を世に知らしめ、世の常識とさせたい。それは　ちょうど天動説が地動説に変わったように　世界史の確かな進化と言えるだろう。

ゼロ除算の研究の進展は、数学的には　佐藤超関数の理論からの展開、発展、　物理学的には　ゼロ除算の物理法則の解釈や、衝突現象における山根の面白い解釈の究明　などに興味が持たれる。しかしながら、ゼロ除算の本質的な解明とは、Aristotélēs　の世界観、universe　は連続である　を否定して、強力な不連続性を　universe　の自然な現象として受け入れられることである。数学では、その強力な不連続性を自然なものとして説明され、解明されることが求められる。

以　上

ゼロ除算は、誰にもわかるが、みんな間違って理解している。

正しい結果は、驚嘆すべきもので、何でも0で割れば、0ということが最近発見された。

ゼロ除算は、不可能であると誰が最初に言ったのでしょうか・・・・

7歳の少女が、当たり前である（100/0=0、0/0=0）と言っているゼロ除算を　多くの大学教授が、信じられない結果と言っているのは、まことに奇妙な事件と言えるのではないでしょうか。

再生核研究所声明２００（2015.1.16）　ゼロ除算と複素解析の現状　―佐藤超関数論との関係が鍵か？

正確に次のように公開して複素解析とゼロ除算の研究を開始した：

特異点解明の歩み100/0=0,0/0=0　関係者：

複素解析学では、1/0として、無限遠点が存在して、美しい世界です。しかしながら、1/0=0　は　動かせない真実です。それで、勇気をもって進まざるを得ない：―　哲学とは　真智への愛　であり、真智とは　神の意志　のことである。哲学することは、人間の本能であり、それは　神の意志　であると考えられる。愛の定義は　声明１４６で与えられ、神の定義は　声明１２２と１３２で与えられている。―　再生核研究所声明１４８．

私には　無理かと思いますが、世の秀才の方々に　挑戦して頂きたい。空論に付き合うのはまっぴらだ　と考える方も多いかと思いますが、面白いと考えられる方で、楽しく交流できれば幸いです。宜しくお願い致します。　添付　物語を続けたい。敬具　齋藤三郎

２０１４．４．１．１１：１０

上記で、予想された難問、　解析関数は、孤立特異点で確定値をとる、が　自分でも予想しない形で解決でき、ある種の実体を捉えていると考えたのであるが、この結果自体、世のすべての教科書の内容を変える事件であるばかりではなく、確立されている無限遠点の概念に　新しい解釈を与えるもので、１次変換の美しい性質が、ゼロ除算の導入によって、任意の１次変換は　全複素平面を全複素平面に１対１　onto　に写すという美しい性質に変わるが、　極である１点において不連続性が現れ、ゼロ除算は、無限を　数から排除する数学になっている。

６月、帰国後、気に成っていた、金子晃先生の　３０年以上前に購入した超函数入門の本に　極めて面白い記述があり、佐藤超関数とゼロ除算の面白い関係が出てきた。さらに　特異積分におけるアダマールの有限部分や、コーシーの主値積分は、弾性体やクラック、破壊理論など広い世界で、自然現象を記述するのに用いられているが、面白いのは　積分が、もともと有限部分と発散部分に分けられ、　極限は　無限たす、有限量の形になっていて、積分は　実は、普通の積分ではなく、そこに現れる有限量を便宜的に表わしている。ところが、その有限量が実は、　ゼロ除算にいう、　解析関数の孤立特異点での　確定値に成っていることが分かった。これはゼロ除算の結果が、広く、自然現象を記述していることを示している。

現在まで、添付２１ページの論文原稿について　慎重に総合的に検討してきた。

そこで、問題の核心、ゼロ除算の発展の基礎は、次の論点に有るように感じられてきた：

We can find many applicable examples, for example, as a typical example in A. Kaneko (\cite{kaneko}, page 11) in the theory of hyperfunction theory: for non-integers $\lambda$, we have

\begin{equation}

x_+^{\lambda} = \left[ \frac{-(-z)^{\lambda}}{2i \sin \pi \lambda}\right] =\frac{1}{2i \sin \pi \lambda}\{(-x + i0)^{\lambda}- (-x - i0)^{\lambda}\}

\end{equation}

where the left hand side is a Sato hyperfunction and the middle term is the representative analytic function whose meaning is given by the last term. For an integer $n$, Kaneko derived that

\begin{equation}

x_+^{n} = \left[- \frac{z^n}{2\pi i} \log (-z) \right],

\end{equation}

where $\log$ is a principal value: $ \{ - \pi < \arg z < +\pi \}$. Kaneko stated there that by taking a finite part of the Laurent expansion, the formula is derived.

Indeed, we have the expansion, for around $ n$, integer

$$

\frac{-(-z)^{\lambda}}{2i \sin \pi \lambda}

$$

\begin{equation}

= \frac{- z^n}{2\pi i} \frac{1}{\lambda -n} - \frac{z^n}{2\pi i} \log (-z )

• \left( \frac{\log^2 (-z) z^n}{2\pi i\cdot 2!} + \frac{\pi z^n}{2i\cdot 3!}

\right)(\lambda - n) + ...

\end{equation}

(\cite{kaneko}, page 220).

By our Theorem 2, however, we can derive this result (4.3) from the Laurant expansion (4.4), immediately.

上記ローラン展開で、\lambda に n　を代入したのが　ちょうど　n に対する佐藤の超関数になっている。それは、ゼロ除算に言う、　孤立特異点における解析関数の極における確定値である。これはゼロ除算そのものと殆ど等価であるから、ローラン展開に　\lambda = n を代入した意味を、上記の佐藤超関数の理論は述べているので　上記の結果を分析すれば、ゼロ除算のある本質を捉えることができるのではないかと考えられる。

佐藤超関数は　日本で生まれた、基本的な数学で　優秀な人材を有している。また、それだけ高級、高度化しているが、このような初歩的、基本的な問題に関係がある事が明らかになってきた。そこで、佐藤超関数論の専門家の方々の研究参加が望まれ、期待される。また、関係者の助言やご意見をお願いしたい。

ゼロ除算における新現象、驚きとは　Aristotélēs　の世界観、universe　は連続である　を否定して、強力な不連続性を　universe　の現象として示していることである。

以　上

7歳の少女が、当たり前であると言っているゼロ除算を　多くの大学教授が、信じられない結果と言っているのは、まことに奇妙な事件と言えるのではないでしょうか。

再生核研究所声明１９９（2015.1.15）　世界の数学界のおかしな間違い、世界の初等教育から学術書まで間違っていると言える　―　ゼロ除算100/0=0,0/0=0

ゼロ除算は　西暦６２８年インドでゼロが文献に記録されて以来、問題とされてきた。ゼロ除算とは、ゼロで割ることを考えることである。これは数学の基本である、四則演算、加法、減法、乗法、除法において、除法以外は何時でも自由にできるのに、除法の場合だけ、ゼロで割ることができないという理由で、さらに物理法則を表す多くの公式にゼロ除算が自然に現れていることもあって、世界各地で、今でも絶えず、問題にされていると考えられる。―　小学生でも　どうしてゼロで割れないのかと毎年、いろいろな教室で問われ続いているのではないだろうか.

これについては、近代数学が確立された以後でも、何百年を越えて　永い間の定説として、ゼロ除算は　不可能であり、ゼロで割ってはいけないことは、初等教育から、中等、高校、大学そして学術界、すなわち、世界の全ての文献と理解はそうなっている。変えることのできない不変的な法則のように理解されていると考えられる。

しかるに２０１４年２月２日　ゼロ除算は、可能であり、ゼロで割ればゼロであることが、偶然発見された。その後の経過、背景や意味付け等を纏めてきた：

再生核研究所声明　148（2014.2.12）　100/0=0, 0/0=0　－　割り算の考えを自然に拡張すると　―　神の意志

再生核研究所声明154（2014.4.22）　新しい世界、ゼロで割る、奇妙な世界、考え方

再生核研究所声明157（2014.5.8） 知りたい　神の意志、ゼロで割る、どうして　無限遠点と原点が一致しているのか？

再生核研究所声明161（2014.5.30）ゼロ除算から学ぶ、数学の精神　と　真理の追究

再生核研究所声明163（2014.6.17）ゼロで割る（零除算）－　堪らなく楽しい数学、探そう零除算　―　愛好サークルの提案

再生核研究所声明166（2014.6.20）ゼロで割る（ゼロ除算）から学ぶ　世界観

再生核研究所声明171（2014.7.30）掛け算の意味と割り算の意味　―　ゼロ除算100/0=0は自明である？

再生核研究所声明176（2014.8.9）　ゼロ除算について、数学教育の変更を提案する

Announcement 179 (2014.8.25): Division by zero is clear as z/0=0 and it is fundamental in mathematics

Announcement 185　: The importance of the division by zero $z/0=0$

再生核研究所声明188（2014.12.1５）ゼロで割る（ゼロ除算）から観えてきた世界

再生核研究所声明190（2014.12.24）

再生核研究所からの贈り物　―　ゼロ除算100/0=0,　0/0=0

夜明け、新世界、再生核研究所　年頭声明

―　再生核研究所声明193（2015.1.1）―　

再生核研究所声明194（2015.1.2）大きなイプシロン（無限小）、創造性の不思議

再生核研究所声明195（2015.1.3）ゼロ除算に於ける高橋の一意性定理について

再生核研究所声明196（2015.1.4）ゼロ除算に於ける山根の解釈100= 0ｘ0について

ところが、気づいてみると、ゼロ除算は当たり前なのに、数学者たちが勝手に、割り算は掛け算の逆と思い込み、ゼロ除算は不可能であると 絶対的な真理であるかのように　烙印を押して、世界の人々も盲信してきた。それで、物理学者が　そのために基本的な公式における曖昧さに困ってきた事情は　ニュートンの万有引力の法則にさえ見られる。

さらに、誠に奇妙なことには、除算はその言葉が表すように、掛算とは無関係に考えられ、日本ばかりではなく西欧でも中世から除算は引き算の繰り返しで計算されてきた、古い、永い伝統がある。その考え方から、ゼロ除算は自明であると道脇裕氏と道脇愛羽さん６歳が（四則演算を学習して間もないときに）理解を示した　―　ゼロ除算は除算の固有の意味から自明であり、ゼロで割ればゼロであるは数学的な真実であると言える（声明１９４）。数学、物理、文化への影響も甚大であると考えられる。

数学者は　数学の自由な精神で　好きなことで、考えられることは何でも考え、不可能を可能にし、分からないことを究め、真智を求めるのが　数学者の精神である。非ユークリッド幾何学の出現で　絶対は変わり得ることを学び、いろいろな考え方があることを学んできたはずである。そのような観点から　ゼロ除算の解明の遅れは　奇妙な歴史的な事件である　と言えるのではないだろうか。

これは、数学を超えた、真実であり、ゼロ除算は不可能であるとの　世の理解は間違っている　と言える。そこで、真実を世界に広めて、人類の歴史を進化させるべきであると考える。特に声明１７６と声明１８５を参照。ゼロ除算は　堪らなく楽しい　新世界　を拓いていると考える。

以　上

ゼロ除算は、不可能であると誰が最初に言ったのでしょうか・・・・

7歳の少女が、当たり前であると言っているゼロ除算を　多くの大学教授が、信じられない結果と言っているのは、まことに奇妙な事件と言えるのではないでしょうか。