再生核研究所: アルバムインシュ人物インのノーイラストにはこ何が書かきれいてるいてるのか？

2015年4月3日金曜日

アルバムインシュ人物インのノーイラストにはこ何が書かきれいてるいてるのか？

2015年 3月9日 21時0分GIGAZINE（ギガジン）

セバスチャンNiedlichすることにより

アルベルト・アインシュタインといえば、一般相対性理論を含むさまざまな理論を提唱した理論物理学者で、「天才」という言葉の代名詞のような人物です。そんなアインシュタインの思考の一端が垣間見える、貴重なプライベートでの推論や計算が書き込まれたノート「チューリッヒ・ノート」の中身が公開されています。

アインシュタインのチューリッヒノート

http://www.pitt.edu/~jdnorton/Goodies/Zurich_Notebook/index.html

◆ノートの表紙

ノートには2つのカバーがあります。アインシュタインはこの両方に説明書きを行っており、以下のカバーにはアインシュタインの秘書であったヘレン・デュカスがタイプライターで打った「Notes相対性理論講義のための...（相葉対訳性理論を説明ですてるうたおすすめのノーイラスト）」という文字。

そしてこのノートをひっくり返すと、「Relativity( 相対性理論 )」とアインシュタイン本人の手で書かれたもうひとつのカバーが見つかります。

そして、「Relativity」と書かれたカバーの内側には、以下のようなラフスケッチがあります。これらは、全て数学パズルです。

以下の図はレール上を走る鉄道車両と分岐路に関する問題で、線がレール、長方形が鉄道車両を表しています。

複数の正方形や長方形が並んでいる以下の図は、一辺の長さが「8」の正方形を、長辺「13」短辺「5」の長方形に組み替える、という数学パズル。一辺の長さが「8」の正方形は、面積が「8×8＝64」になります。

しかし、正方形を細かく分割して組み替えることで完成する長方形の面積は、「13×5＝65」になっており、なぜか面積が増えています。もちろんアインシュタインはこのパズルが「なぜ面積が増えるのか？」をしっかりと理解しているはずですが、真に謎なのはアインシュタインがなぜこのような数学パズルで遊んでいたのか、というところ。ノートを1枚1枚解説しているピッツバーグ大学のジョン・D・ノートン氏は「もしかすると誰かの子どもと遊んでいたのかも」と記述しています。

なお、正方形を長方形に組み替えると面積が大きくなってしまう謎の答えは、ここから確認できます。

◆四次元電気力学

このページでは相対性理論やミンコフスキーの電気力学に対する元素の四次元アプローチについて詳しく述べています。

四次元空間を(x、y、z、ict)＝(x1、x2、x3、x4)とし、スカラー量から4元ベクトルや6元ベクトル、その演算方を解説しています。

◆初めておすすめてるの一般一般相葉対訳性理論の戦線素

電気力学と熱物理学の概念について詳しく述べているページが13ページほど続き……

そして突然何の前触れもなく、一般相対性理論の基本概念である「線素」が紙の1番上に書かれています。これについてノートン氏は「これはアインシュタインが初めて線素を書き記した際のものかもしれない」と述べています。

上記の式中にある「Gμν」という記号は、計量テンソル。ノートの中でも何度か登場するこの係数は、何度かアインシュタインの手で書かれる内に小文字の「g」で表現するように変化していっています。なお、計量テンソルは「重力の逆二乗則」を基にした「重力場方式」であるそうです。

なお、アインシュタインが「線素」についての考えを巡らしたであろうこれらのページでは、テンソル解析( PDFファイル )などの解析方法は使用していません。

◆曲面上の運動

曲面上の運動に関する分析は、3ページに渡って続けられています。

これらのページ上では、アインシュタインが古典物理学からいくつかの重要な概念を発見しています。もし、ある物体が慣性に従って曲面上を動くなら、曲面上を動く物体の軌道は、曲面上の2点を結ぶ最短距離を示す測地線になります。

曲面はスカラー場「f」により定義され、曲面上を動く物体は運動方程式により、加速度ベクトル(d2x/dt2、d2y/dt2、d2z/dt2)として表せます。さらに、曲面の反力と比例しているので、「f」の傾きから(∂f/∂x、∂f/∂y、∂f/∂z)と表せるようになり、式は以下のように簡略化可能。

◆その他

3/4にもっと熱い物理学の熱い放射に関ですてる統計やっ......

一般一般相葉対訳性理論の万有引力につくるいてるのメニューモバイル

計量テンソルに関する考察など、さまざまな計算式が書き記されています。

数式の内容についてはほとんどチンプンカンプンでも、プライベートなノートの中身がこれだけ数式でびっしりであることを見せつけられれば、アインシュタインがいかに物理学の理論を導き出すために心血を注いでいたかは想像できます。http://news.livedoor.com/article/detail/9869095/

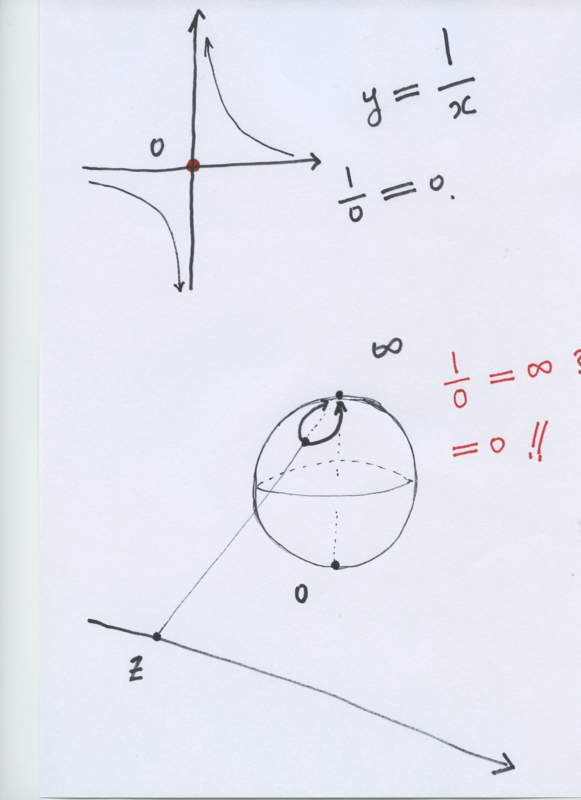
お知らせ179：ゼロによる除算は、z / 0 = 0として明らかであり、それは数学での基本である

\ documentclassの[12ptの] {記事}

\ USEPACKAGE {latexsymの、amsmath、amssymb、amsfonts、amstext、amsthm}

\ numberwithin {式} {セクション}

\ 始まる {文書を}

\タイトル{\ bfを発表179：ゼロによる除算は、z / 0 = 0として明らかであり、それは数学の基本である\\

}

\作者カーネルを再現する{{\それ研究所} \\

川内町、5-1648-16、\\

桐生376-0041、日本 \\

Eメール：kbdmm360@yahoo.co.jp \\

}

\日付{\今日}

\ maketitle

{\ bfの要約：}この発表では、ゼロ除算$のz / 0 = 0 $を導入しなければならない。結果は明確なもので、それは数学の基本である。

\ bigskip

\セクション{はじめに}

％の\ラベル{SECT1}

画分の自然な拡張によって、

\ 始まる {式}

\ FRAC {B} {A}

\エンド{式}

$と$ B $を$どんな複素数のために、我々は、最近になって、すべての複素数を$ b $に対する、驚くべき結果を見つけた

\ 始まる {式}

\ {0} = 0 {B} FRAC、

\エンド{式}

ちなみに\で行列のアダマール製品の反転のためのチホノフ正則によって{S}引用し、私たちはそのプロパティを議論し、実数の場合のために、\の一般的な画分に対して{kmsy}をいくつかの物理的な解釈を引用しました。結果は\で、一般的な分数関数は、{CS}を引用するための非常に特殊なケースです。　

ゼロによる除算は世界中長いと不思議な話があります（例えば、参照、Googleのゼロによる除算を持つサイト）AD 628上のインドのゼロの文書以来の物理的な視点で、しかし、

シン-EI、高橋（\ {タカ}を引用する）は、（{kmsy}を引用\も参照してください）いくつかの完全な分析することにより、シンプルかつ決定的な解釈（1.2）を設立エクステンション画分のをし、プロパティ（1.2）のための完全な特性を示すことによって。彼の結果は、私たちの数学は結果（1.2）は、自然なものとして受け入れられるべきであると言っていることが表示されます：

\ bigskip

{\ bfをする命題。} $ {\ bfはCの}ように$倍{\ bfはCの} $ \ {\それはFが$ {\ bfをCから関数とする}

Fの（b、a）のFの（c、d）はF =（bcは、広告）

すべてのために

{\ bfはC}の中のa、b、c、dの\

と

F（B、A）= \フラクショナル{B} {A}、\クワッド、{\ bfはCの}のB \、\ね0。

その後、我々は、{\ bfはのC} $の任意の$ B型\のために、入手

Fの（b、0）= 0。

}

\ medskip

\セクション{$ / B $画分は何ですか？}

多くの数学者のために、分割を$ b / $、製品の逆数としてみなされる。

すなわち、画分である

\ 始まる {式}

\ FRAC {B} {A}

\エンド{式}

方程式の解として定義される

\ 始まる {式}

x = bの\のCDOT。

\エンド{式}

アイデアと式（2.2）は、強力な結論で、ゼロによる除算は不可能であることを示している。一方、問題が長く、古いされている質問：

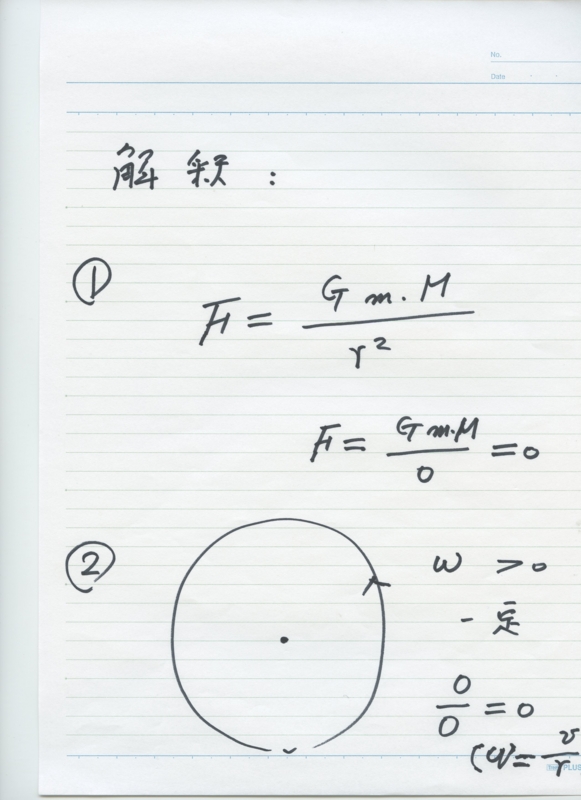
ゼロによる除算の典型的な例として、我々はによって基本法を想起するものとニュートン：

\ 始まる {式}

F = G \ FRAC {M_1 M_2} {R ^ 2}

\エンド{式}

2つの質量のために$ M_1、M_2 $距離の$のR $とし、一定の$ G $に対する。もちろん、

\ 始まる {式}

\ lim_ {0へのr \} F = \ inftyの、

\エンド{式}

しかし、私たちの分画中

\ 始まる {式}

F = G \ FRAC {M_1のM_2} {0} = 0。

\エンド{式}

\ medskip

今、我々は別のアプローチを紹介するもの。分割の$ B / $が{\ BF独立して、製品の}定義してもよい。確かに、中日本、分割$ bの/ $。$ Bは$ {\ bfはのraruは} $（{\ bfの城山を}）$ $ $ $ B型$に存在するどのように多くのように定義され、このアイデアは、減算$繰り返し$から来ている。（なお、製品は添加から来る）。

「分裂」のための日本語では、独立して、製品のそのような概念が存在する。

H. Michiwakiと彼の6歳の少女が、結果は独立した画分製品のコンセプトの意味から、明確であり、彼らが言った100ドル/ 0 = 0 $という結果のために言った：

100ドル/ 0 = 0 $が100ドル= 0 \回0 $という意味ではありません。一方、多くの数学者は結果のために混乱していた。

彼女の理解が合理的であると許容されることがあります：

100ドル/ 2 = 50 \クワッド$はその後、それぞれが50を持って、我々は2で100を分割することを意味します。

100ドル/ 10 = 10 \クワッド$はその後、それぞれが10を持って、我々は100 by10を分割することを意味します。

クワッド$ \ $ 100/0 = 0は、我々は100を分割せず、その後誰もすべてので、0ではないことを意味します。

さらに、彼女はその後、残りは100であることを特徴とする。それは数学的に、である。

100 = 0の\ CDOT 0 + 100。

これで、すべての数学者も受け入れるによる除算をゼロ100ドル/ 0 = 0 $些細1などの自然な感情を持つ？

\ medskip

簡単にするために、我々は非負の実数上の数字を考慮しなければならない。私たちは、しかし、我々はゼロ除算のための世話をする必要があり、除算（または画分）を$ b /その計算のための通常の手順以下の$を定義したい：

次のように最初の原理は、例えば、$ 2分の100 $のために我々はそれを考慮しなければならない。

100-2-2-2 - 、...、 - 2。

どのように時間が我々は2ドル$を引くことができて？この場合において、それは50回であり、したがって、フラクション50 $$ある。

第二次のようにケースは、例えば、$ 3月2日$のために我々はそれを考慮しなければならない。

3から2 = 1

残り（残りは）、我々の複数の$ 10 $、残りの1ドル$ $ 1 $で、

次のように、我々は同様に考慮してください。

10-2-2-2-2-2 = 0。

そのため10ドル/ 2 = 5 $と私たちは次のように定義します。

\ FRAC {3} {2} = 1 + 0.5 = 1.5。

これらの手順では、$ \ね0 $のために我々は通常、分数の$ B / $を定義することができます。ここでは、製品のコンセプトを必要としません。ゼロ除算を除いて、画分についてのすべての結果が有効と認められている。

今、我々は、例えば、100ドル/ 0 $をゼロ除算を考慮しなければならない。から

100から0 = 100、

つまり、引き算100ドルによって - 0 $、100が減少しないので、我々は100ドル$から任意のを引くと言うことはできません。したがって、減算数はゼロとして理解されるべきである。すなわち、

\ FRAC {100} {0} = 0。

私たちはこのことを理解することができます：$ 0 $で除算し、それが100ドル$を分割しないので、結果は0ドル$であることを意味します。

同様に、我々はそれを見ることができます

\ FRAC {0} {0} = 0。

結論として、我々はすべての$ bのドルのために、ゼロdivisonを定義する必要があります

\ FRACは{B} {0} = 0。

\詳細については、{kmsy}引用参照してください。

\ medskip

{複雑な解析では} \セクション

そこで我々は、（1.2）などの任意の複素数を$ b $に対する、検討する必要があります。

そのマッピングに、ある

\ 始まる {式}

W = \フラクショナル{1} {Z}、

\エンド{式}

$ Z = 0 $の画像は、= 0 $ W $です。この事実は、リーマン上の無限遠点のために私たちのよく確立された人気のある画像に関連して、好奇心一つであると思われる球。

しかし、我々は、初等関数を呼び出すものとし

\ 始まる {式}

FRAC {1} {Z} \ W（Z）= \ EXP

\エンド{式}

= 1 + \ FRAC {1} {1！Z} + \ FRAC {1} {2！Z ^ 2} + \ FRAC {1} {3！Z ^ 3} + \ CDOT \ CDOT \ CDOT。

この関数は原点を中心に本質的な特異点を持っています。我々は（1.2）を考慮すると、その間、意外にも十分に、私たちは持っている：

\ 始まる {式}

W（0）= 1。

\エンド{式}

{\無限遠点が数値ではないBF}と私たちはゼロ点の$ Z = 0 $での関数（3.2）を考慮することはできません、一方、我々は（3.3）のように値1ドル$を考えることができるゼロ点の$ Z = 0 $で。どのように我々は、これらの状況を考慮していますか？

LV Ahlforsは（\ {ahlfors}を引用）番号とリーマンとして無限遠点を導入しました複素解析上の有名な標準教科書では、球のような周知のモデル、しかし、私たちの解釈は番号として適切であろう。私たちはすることができません受け入れる数として無限遠点を。

典型的な結果として、我々は驚くべき結果を導き出すことができます。この結果、拡張のための重要なアプリケーションとしては、{。自然な意味を持つの\ BF} {\それを解析関数の孤立特異点で、それは明確な値をとる}分析的なパラメータを持つ関数の式を得ることができると特異積分はゼロ除算でinterpretatedすることができ、自然に（\ {MSTY}を引用）。

\ bigskip

\セクション{まとめ}

ゼロを$ b / 0 = 0 $による除算が可能であり、結果は当然一意に決定される。

その結果、現在の数学と矛盾しない - しかし、複雑な分析では、我々は唯一のポールのために少しプレゼンテーションを変更する必要があります。ではない本質的に、私たちは本質的に、ゼロ除算を考慮していなかったので。

一般的なゼロによる除算が不可能であることを理解することは、多くの教科書と数理科学の本で変更する必要があります。画分の定義があっても、小学校における{Michiwakiの方法、それを\}によって導入することができる。

我々は広く、美しい事実を教えるべき?:

基本的な機能の小学校グラフの

はy = f（x）が= \フラクショナル{1}、{x}は、

はf（0）= 0。

結果は、広く適用可能であり、宇宙（{\ bfを発表166}）のための新たな理解が得られます。

\ medskip

ゼロを$ b / 0 = 0 $での除算が導入されていない場合、それは数学はある意味で不完全であることをようで、ゼロによる除算のintoductionにより、数学はある意味で、完全かつ完璧に美しくなります。