-世界観の拡大を世界地図の歴史でながめると-
ヘカタイオスの世界地図 ヘロドトスの世界像 エラトステネスの世界図 プトレマイオスの世界図
イドリーシーの円形世界図 トスカネリの地図 シェーナーの世界図 メルカトルの世界図 テイセイラの日本図
(これらの図版は、『世界史地図・図解集』・『基本白地図』にも収録されています)
ヘカタイオスの世界地図
ヘカタイオスの世界地図
世界地図を最初につくったのはバビロニア人ですが,ギリシア人もすぐに,地図製作の技術を発達させました。この地図はヘカタイオスの考案にもとづくもので,政治上の意思決定に利用するためにつくられました。ヘロドトスによれば,この地図は青銅板に彫られており,ペルシア人の支配に抵抗してイオニアのギリシア人植民市が反乱をおこした(前499~前494)さいに,ミレトスのアリスタゴラスがスパルタに運びました。
ヘカタイオス(前550?~前475?)はギリシア最古の歴史家で,最古の散文家の一人です。ミレトス出身で,政治家としてイオニア植民市の反乱にも関与しました。ひろく旅行し,世界地誌で地図も含む『世界周遊』と歴史的著作『系譜』を著し,ヘロドトスに影響をあたえ,彼の仕事の先駆となりました。
ヘロドトスの世界像
ヘロドトスの世界像
ヘロドトス(前485ころ~前425ころ)は小アジアのハリカルナソス出身の歴史家です。ペルシア戦争を主題に,自らの大旅行の見聞を交えた『歴史』を著しました。これは世界最古の個人による体系的な歴史叙述にあたり,彼は「歴史記述の祖」と呼ばれています。彼の旅行は北は黒海北岸から南はアフリカ北岸のキレネ,エジプト南端のエレファンティネにおよび,フェニキアのティルス,ガザからメソポタミアのバビロンに及んだと推定されます。しかし小アジアの内陸部やアケメネス朝ペルシアの都スサ,また西方ではシチリア島は訪れていません。
エラトステネスの世界図
エラトステネスの世界図
アレクサンドリアのムセイオンの館長を務めたエラトステネス(前275ころ~前194)の世界図は現存しません。ギリシア人地理学者ストラボン(前64~後21ころ)の『地理誌』によって復元したものです。初期のギリシア人は大地を円盤のようなものとみなしていたことは,前6世紀のヘカタイオスの地理書から復元した世界図によって知られています。しかしギリシアではアリストテレスによって地球が球体をなすことが認められました。さらにエラトステネスが前3世紀に地球の大きさを測定し,実際の地球の大きさ約4万kmと比較して,1割ほど過大な44500kmとし,古代としては驚くほど正確な結果を得ました。
プトレマイオスの世界図
プトレマイオスの世界図
プトレマイオス(生没年不詳)はアレクサンドリアで活動した,2世紀のギリシアの天文学者,地理学者,数学者です。彼の地球は球形で宇宙の中心に静止しているとする天動説は,コペルニクスが現れるまで絶対的権威を持ちました。プトレマイオスは地図の円錐投影法を考察し,当時ヨーロッパ人に知られていた世界の約8000の地点の緯度・経度を推定して,東はシルクロードを通じての知識によって「絹の国」の中国まで描かれています。しかしアフリカは赤道以南では無限に広がり,またインド洋は内海として描かれています。またインド半島が東西に連なる平坦な海岸線で描かれていたり,アフリカ内部の「月の山脈」から流出するナイル川の2本の源流がともに湖に流入してから北流していくように描かれています。
イドリーシーの円形世界図
イドリーシーの円形世界図
12世紀にイドリーシーはシチリア王国のルッジェーロ2世(在位1130~54)の命を受けて,銀盤に彫られた世界の平面球形図を作成します。プトレマイオスの世界図にイスラームの地理的知識を加えて描かれたもので,プトレマイオスの世界図では内海となっているインド洋が外海に通じ,アフリカの最東端にワクワク(倭国?)を記載しています。これが日本であるとすれば,西方の地図に日本が記された最初です。バグダードとイベリア半島のトレドの間で3度の誤差しかないほど,緯度表記は非常に正確です。イドリーシー(1100~65/66)はイスラームの地理学者で,モロッコのセウタの名門出身です。当時イスラーム学芸の中心地であったイベリア半島のコルドバで学び,イベリア半島各地,アフリカ北岸,小アジア,英仏海岸などを実地に見聞した後,シチリアのノルマン王ルッジェーロ2世に仕えます。
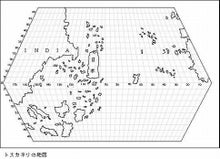
トスカネリの地図
トスカネリの地図
トスカネリ(1397~1482)はフィレンツェの天文・地理学者で,地球球体説を主張し,コロンブスに西まわりルート(大西洋航路)を選ばせる論拠を与えたとされます。この地図は1474年コロンブスがトスカネリによって贈られたものとされるものです。この地図によれば,アフリカ西岸から西へ向かって経度にして90度の距離にジパング(日本)が描かれており,アメリカ大陸の存在は示されていないので大西洋を西へ西へと向かって行けばジパングに到達することになります。東まわりで陸路を行くよりは,早く確実に行けるとコロンブスは確信したのも無理はなかったのでしょう。ただし,この地図は後世の偽作であるともいわれています。
シェーナーの世界図
シェーナーの世界図
シェーナーの1523年作成による木版刷地球儀ゴアの世界図であり,マゼランの世界周航(1519~22年)の航路が描かれています。南半球の大部分は依然として不明で残されています。北半球の大陸と対応して,南半球にも巨大な大陸が存在すると想像されたギリシア以来の考えが復活して,この世界図には南半球に架空の「南方大陸(テラ・アウストラリス)」が大きく描かれています。しかし18世紀には,クックの3回にわたる太平洋の探検航海によって,南方大陸は幻想の大陸として消失し,それにかわってオーストラリア大陸の実在することが明らかとなりました。
メルカトルの世界図
メルカトルの世界図
1569年に,フランドルの地理学者メルカトルによって正角円筒図法による銅版の世界図(126×200cm)が製作されました。すでにこのときまでに,コロンブスによるアメリカ大陸の発見やヴァスコ=ダ=ガマによるインド航路の開拓,マゼラン一行による世界周航がおこなわれ,アジアやアフリカの知識も正確になっていました。しかし,オーストラリアや南極はいまだ知られて折らず,この地図では架空の大陸が描かれています。また日本の存在は知られており,この地図にも描かれています。中世以降,北極探検は東アジアへの最短路の開拓や捕鯨,毛皮猟などの目的として行われました。その北極地が海洋であることは,1895年ナンセンが確かめ,1909年ピアリが初めて北極点に到達しました。
テイセイラの日本図
テイセイラの日本図
1595年のオルテリウスの地図帳所蔵のテイセイラの日本図は,ヨーロッパで刊行された日本のみを単独に示した最初の日本図です。日本の太平洋岸に架空の島が描かれています。西方の世界に日本が知られるようになったのは,9世紀に世界のいちばん東にワクワク(倭国)という国があるとアラビア人によって伝えられたのが最初であるとみなされています。またヨーロッパに日本のことを黄金国チパングとして伝えたのはマルコ=ポーロです。やがてアジアに進出したポルトガルは,中国人を通じて中国の東にジャパンという国が存在することを知るようになります。そして1543年のポルトガル人の種子島渡来をさきがけとして,ポルトガル船の来航やキリスト教宣教師の来日によって,実際の日本についての知識がヨーロッパに伝えられました。また実測による正確な形状の日本がヨーロッパにも知られるようになったのは,高橋景保から贈られた伊能図を基礎にしてシーボルトが作成した日本図です。http://www007.upp.so-net.ne.jp/snakayam/map_history.html
再生核研究所声明199(2015.1.15) 世界の数学界のおかしな間違い、世界の初等教育から学術書まで間違っていると言える ― ゼロ除算100/0=0,0/0=0
ゼロ除算は 西暦628年インドでゼロが文献に記録されて以来、問題とされてきた。ゼロ除算とは、ゼロで割ることを考えることである。これは数学の基本である、四則演算、加法、減法、乗法、除法において、除法以外は何時でも自由にできるのに、除法の場合だけ、ゼロで割ることができないという理由で、さらに物理法則を表す多くの公式にゼロ除算が自然に現れていることもあって、世界各地で、今でも絶えず、問題にされていると考えられる。― 小学生でも どうしてゼロで割れないのかと毎年、いろいろな教室で問われ続いているのではないだろうか.
これについては、近代数学が確立された以後でも、何百年を越えて 永い間の定説として、ゼロ除算は 不可能であり、ゼロで割ってはいけないことは、初等教育から、中等、高校、大学そして学術界、すなわち、世界の全ての文献と理解はそうなっている。変えることのできない不変的な法則のように理解されていると考えられる。
しかるに2014年2月2日 ゼロ除算は、可能であり、ゼロで割ればゼロであることが、偶然発見された。その後の経過、背景や意味付け等を纏めてきた:
再生核研究所声明 148(2014.2.12) 100/0=0, 0/0=0 - 割り算の考えを自然に拡張すると ― 神の意志
再生核研究所声明154(2014.4.22) 新しい世界、ゼロで割る、奇妙な世界、考え方
再生核研究所声明157(2014.5.8) 知りたい 神の意志、ゼロで割る、どうして 無限遠点と原点が一致しているのか?
再生核研究所声明161(2014.5.30)ゼロ除算から学ぶ、数学の精神 と 真理の追究
再生核研究所声明163(2014.6.17)ゼロで割る(零除算)- 堪らなく楽しい数学、探そう零除算 ― 愛好サークルの提案
再生核研究所声明166(2014.6.20)ゼロで割る(ゼロ除算)から学ぶ 世界観
再生核研究所声明171(2014.7.30)掛け算の意味と割り算の意味 ― ゼロ除算100/0=0は自明である?
再生核研究所声明176(2014.8.9) ゼロ除算について、数学教育の変更を提案する
Announcement 179 (2014.8.25): Division by zero is clear as z/0=0 and it is fundamental in mathematics
Announcement 185 : The importance of the division by zero $z/0=0$
再生核研究所声明188(2014.12.15)ゼロで割る(ゼロ除算)から観えてきた世界
再生核研究所声明190(2014.12.24)
再生核研究所からの贈り物 ― ゼロ除算100/0=0, 0/0=0
夜明け、新世界、再生核研究所 年頭声明
― 再生核研究所声明193(2015.1.1)―
再生核研究所声明194(2015.1.2)大きなイプシロン(無限小)、創造性の不思議
再生核研究所声明195(2015.1.3)ゼロ除算に於ける高橋の一意性定理について
再生核研究所声明196(2015.1.4)ゼロ除算に於ける山根の解釈100= 0x0について
ところが、気づいてみると、ゼロ除算は当たり前なのに、数学者たちが勝手に、割り算は掛け算の逆と思い込み、ゼロ除算は不可能であると 絶対的な真理であるかのように 烙印を押して、世界の人々も盲信してきた。それで、物理学者が そのために基本的な公式における曖昧さに困ってきた事情は ニュートンの万有引力の法則にさえ見られる。
さらに、誠に奇妙なことには、除算はその言葉が表すように、掛算とは無関係に考えられ、日本ばかりではなく西欧でも中世から除算は引き算の繰り返しで計算されてきた、古い、永い伝統がある。その考え方から、ゼロ除算は自明であると道脇裕氏と道脇愛羽さん6歳が(四則演算を学習して間もないときに)理解を示した ― ゼロ除算は除算の固有の意味から自明であり、ゼロで割ればゼロであるは数学的な真実であると言える(声明194)。数学、物理、文化への影響も甚大であると考えられる。
数学者は 数学の自由な精神で 好きなことで、考えられることは何でも考え、不可能を可能にし、分からないことを究め、真智を求めるのが 数学者の精神である。非ユークリッド幾何学の出現で 絶対は変わり得ることを学び、いろいろな考え方があることを学んできたはずである。そのような観点から ゼロ除算の解明の遅れは 奇妙な歴史的な事件である と言えるのではないだろうか。
これは、数学を超えた、真実であり、ゼロ除算は不可能であるとの 世の理解は間違っている と言える。そこで、真実を世界に広めて、人類の歴史を進化させるべきであると考える。特に声明176と声明185を参照。ゼロ除算は 堪らなく楽しい 新世界 を拓いていると考える。
以 上
1+0=1 1ー0=0 1×0=0 では、1/0・・・・・・・・・幾つでしょうか。
0??? 本当に大丈夫ですか・・・・・0×0=1で矛盾になりませんか・・・・
1/0=∞ (これは、今の複素解析学) 1/0=0 (これは、新しい数学で、Division by Zero)
ゼロ除算は、不可能であると誰が最初に言ったのでしょうか・・・・
7歳の少女が、当たり前であると言っているゼロ除算を 多くの大学教授が、信じられない結果と言っているのは、まことに奇妙な事件と言えるのではないでしょうか。
割り算を掛け算の逆だと定義した人は、誰でしょう???
世界中で、ゼロ除算は 不可能 か
可能とすれば ∞ だと考えられていたが・・・
しかし、ゼロ除算 はいつでも可能で、解は いつでも0であるという意外な結果が得られた。
小学校以上で、最も知られている数学の結果は何でしょうか・・・
ゼロ除算(1/0=0)は、ピタゴラスの定理(a2 + b2 = c2 )を超えた基本的な結果であると考えられる。
https://www.pinterest.com/pin/234468724326618408/
原点を中心とする単位円に関する原点の鏡像は、どこにあるのでしょうか・・・・
∞ では無限遠点はどこにあるのでしょうか・・・・・
無限遠点は存在するが、無限大という数は存在しない・・・・
加(+)・減(-)・乗(×)・除(÷) 除法(じょほう、英: division)とは、乗法の逆演算・・・・間違いの元 乗(×)は、加(+) 除(÷)は、減(-)
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1411588849/a37209195?sort=1&fr=chie_my_notice_canso
地球平面説→地球球体説
天動説→地動説
1/0=∞ 若しくは未定義 →1/0=0
地球人はどうして、ゼロ除算1300年以上もできなかったのか? 2015.7.24.9:10 意外に地球人は知能が低いのでは? 仲間争いや、公害で自滅するかも。 生態系では、人類が がん細胞であった とならないとも 限らないのでは?
地球平面説→地球球体説
地球が丸いと考えた最初の人-ピタゴラス
地球を球形であることを事実によって証明しようとした人-マゼラン
地球を球形と仮定して初めて地球の大きさを測定した人-エラトステネス
天動説→地動説 アリスタルコス=ずっとアリストテレスやプトレマイオスの説が支配的だったが、約2,000年後にコペルニクスが再び太陽中心説(地動説)を唱え、発展することとなった。https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%AA%E3%82%B9%E3%82%BF%E3%83%AB%E3%82%B3%E3%82%B9 …
何年かかったでしょうか????
1/0=∞若しくは未定義 →1/0=0
何年かかるでしょうか????
地球平面説→地球球体説
天動説→地動説
何年かかったでしょうか???
1/0=∞若しくは未定義 →1/0=0
何年かかるでしょうか???
再生核研究所声明200(2015.1.16) ゼロ除算と複素解析の現状 ―佐藤超関数論との関係が鍵か?
正確に次のように公開して複素解析とゼロ除算の研究を開始した:
特異点解明の歩み100/0=0,0/0=0 関係者:
複素解析学では、1/0として、無限遠点が存在して、美しい世界です。しかしながら、1/0=0 は 動かせない真実です。それで、勇気をもって進まざるを得ない:― 哲学とは 真智への愛 であり、真智とは 神の意志 のことである。哲学することは、人間の本能であり、それは 神の意志 であると考えられる。愛の定義は 声明146で与えられ、神の定義は 声明122と132で与えられている。― 再生核研究所声明148.
私には 無理かと思いますが、世の秀才の方々に 挑戦して頂きたい。空論に付き合うのはまっぴらだ と考える方も多いかと思いますが、面白いと考えられる方で、楽しく交流できれば幸いです。宜しくお願い致します。 添付 物語を続けたい。敬具 齋藤三郎
2014.4.1.11:10
上記で、予想された難問、 解析関数は、孤立特異点で確定値をとる、が 自分でも予想しない形で解決でき、ある種の実体を捉えていると考えたのであるが、この結果自体、世のすべての教科書の内容を変える事件であるばかりではなく、確立されている無限遠点の概念に 新しい解釈を与えるもので、1次変換の美しい性質が、ゼロ除算の導入によって、任意の1次変換は 全複素平面を全複素平面に1対1 onto に写すという美しい性質に変わるが、 極である1点において不連続性が現れ、ゼロ除算は、無限を 数から排除する数学になっている。
6月、帰国後、気に成っていた、金子晃先生の 30年以上前に購入した超函数入門の本に 極めて面白い記述があり、佐藤超関数とゼロ除算の面白い関係が出てきた。さらに 特異積分におけるアダマールの有限部分や、コーシーの主値積分は、弾性体やクラック、破壊理論など広い世界で、自然現象を記述するのに用いられているが、面白いのは 積分が、もともと有限部分と発散部分に分けられ、 極限は 無限たす、有限量の形になっていて、積分は 実は、普通の積分ではなく、そこに現れる有限量を便宜的に表わしている。ところが、その有限量が実は、 ゼロ除算にいう、 解析関数の孤立特異点での 確定値に成っていることが分かった。これはゼロ除算の結果が、広く、自然現象を記述していることを示している。
現在まで、添付21ページの論文原稿について 慎重に総合的に検討してきた。
そこで、問題の核心、ゼロ除算の発展の基礎は、次の論点に有るように感じられてきた:
We can find many applicable examples, for example, as a typical example in A. Kaneko (\cite{kaneko}, page 11) in the theory of hyperfunction theory: for non-integers $\lambda$, we have
\begin{equation}
x_+^{\lambda} = \left[ \frac{-(-z)^{\lambda}}{2i \sin \pi \lambda}\right] =\frac{1}{2i \sin \pi \lambda}\{(-x + i0)^{\lambda}- (-x - i0)^{\lambda}\}
\end{equation}
where the left hand side is a Sato hyperfunction and the middle term is the representative analytic function whose meaning is given by the last term. For an integer $n$, Kaneko derived that
\begin{equation}
x_+^{n} = \left[- \frac{z^n}{2\pi i} \log (-z) \right],
\end{equation}
where $\log$ is a principal value: $ \{ - \pi < \arg z < +\pi \}$. Kaneko stated there that by taking a finite part of the Laurent expansion, the formula is derived.
Indeed, we have the expansion, for around $ n$, integer
$$
\frac{-(-z)^{\lambda}}{2i \sin \pi \lambda}
$$
\begin{equation}
= \frac{- z^n}{2\pi i} \frac{1}{\lambda -n} - \frac{z^n}{2\pi i} \log (-z )
- \left( \frac{\log^2 (-z) z^n}{2\pi i\cdot 2!} + \frac{\pi z^n}{2i\cdot 3!}
\right)(\lambda - n) + ...
\end{equation}
(\cite{kaneko}, page 220).
By our Theorem 2, however, we can derive this result (4.3) from the Laurant expansion (4.4), immediately.
上記ローラン展開で、\lambda に n を代入したのが ちょうど n に対する佐藤の超関数になっている。それは、ゼロ除算に言う、 孤立特異点における解析関数の極における確定値である。これはゼロ除算そのものと殆ど等価であるから、ローラン展開に \lambda = n を代入した意味を、上記の佐藤超関数の理論は述べているので 上記の結果を分析すれば、ゼロ除算のある本質を捉えることができるのではないかと考えられる。
佐藤超関数は 日本で生まれた、基本的な数学で 優秀な人材を有している。また、それだけ高級、高度化しているが、このような初歩的、基本的な問題に関係がある事が明らかになってきた。そこで、佐藤超関数論の専門家の方々の研究参加が望まれ、期待される。また、関係者の助言やご意見をお願いしたい。
ゼロ除算における新現象、驚きとは Aristotélēs の世界観、universe は連続である を否定して、強力な不連続性を universe の現象として示していることである。
以 上
7歳の少女が、当たり前であると言っているゼロ除算を 多くの大学教授が、信じられない結果と言っているのは、まことに奇妙な事件と言えるのではないでしょうか。
世界中で、ゼロ除算は 不可能 か
可能とすれば ∞ だと考えられていたが・・・
しかし、ゼロ除算 はいつでも可能で、解は いつでも0であるという意外な結果が得られた。
1/0=∞ (これは、今の複素解析学) 1/0=0 (これは、新しい数学で、Division by Zero)
原点を中心とする単位円に関する原点の鏡像は、どこにあるのでしょうか・・・・
∞ では無限遠点はどこにあるのでしょうか・・・・・
無限遠点は存在するが、無限大という数は存在しない・・・・
地球平面説→地球球体説
天動説→地動説
何年かかったでしょうか????
1/0=∞若しくは未定義 →1/0=0
何年かかるでしょうか????
\documentclass[12pt]{article}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 247: The gradient of y-axis is zero and $\tan (\pi/2) =0$ by the division by zero $1/0=0$}
\author{{\it Institute of Reproducing Kernels}\\
\date{September 22, 2015}
\maketitle
In Announcement 246, we stated:
\medskip
Consider the lines $y = ax$ with gradients $a$ through the origin $ 0$. Consider the two limits that $a \quad (>0)$ tends to $ + \infty$ and $a \quad (<0)$ tends to $- \infty$, respectively. As their limits, we see that the limiting lines are $y$ — axis. Note that the gradient of the $y$ axis is zero, not infinity.
This example shows as in the graph of the function $y = f(x) = 1/x$ at $x = 0$ as $f(0) =0$, that was introduced by the division by zero $1/0=0$ mathematically (\cite{s,kmsy,ttk,ann}).
\medskip
For this announcement, Professor H. Begehr kindly referred to the gradient of the $y$ axis in the above: If the gradient of the imaginary axis is $0$ this would mean $\tan (\pi/2)=0$,
right? Of course this would be a consequence of $1/0=0$!
\medskip
We had sent the e-mail, soon as follows:
\medskip
For the gradient of $y$ axis, we can define it as zero, very naturally and in the intuitive sense; of course, we can give its definition precisely.
However, as you stated, we can derive it formally by the division by zero $1/0=0$; this deduction will be very interested in itself, because, the formal result $1/0=0$ is coincident with the natural sense.
\medskip
The gradients of y axis and x axis are both zero.
\medskip
Surprisingly enough, this would mean $\tan (\pi/2)=0$,
right?
THIS IS RIGHT for our sense; we gave the definition of the values for analytic functions at an isolated singular point:
\medskip
{\bf Theorem :} {\it Any analytic function takes a definite value at an isolated singular point }{\bf with a natural meaning.} The definite value is given by the first coefficient of the regular part in the Laurent expansion around the isolated singular point (\cite{ann}).
\medskip
As the fundamental results, we would like to state that
\medskip
{\huge \bf I) The gradient of the y axis is zero,}
\medskip
and
\medskip
{\huge \bf II) $\tan \frac{\pi}{2} = 0,$}
\medskip
in the sense of the division by zero in our sense.
\medskip
Note that the function $y = \tan x$ is similar with the function $y = 1/x$ around $x = \frac{\pi}{2}
$ and $ x = 0$, respectively.
\footnotesize
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95. http://www.scirp.org/journal/ALAMT/
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operators on the real and complex fields, Tokyo Journal of Mathematics (in press).
\bibitem{ann}
Announcement 185: Division by zero is clear as z/0=0 and it is fundamental in mathematics,
Institute of Reproducing Kernels, 2014.10.22.
\end{thebibliography}
\end{document}
\usepackage{latexsym,amsmath,amssymb,amsfonts,amstext,amsthm}
\numberwithin{equation}{section}
\begin{document}
\title{\bf Announcement 246: An interpretation of the division by zero $1/0=0$ by the gradients of lines }
\author{{\it Institute of Reproducing Kernels}\\
\date{September 17, 2015}
\maketitle
Consider the lines $y = ax$ with gradients $a$ through the origin $ 0$. Consider the two limits that $a \quad (>0)$ tends to $ + \infty$ and $a \quad (<0)$ tends to $- \infty$, respectively. As their limits, we see that the limiting lines are $y$ — axis. Note that the gradient of the $y$ axis is zero, not infinity.
This example shows the graph of the function $y = f(x) = 1/x$ at $x = 0$ as $f(0) =0$, that was introduced by the division by zero $1/0=0$ mathematically (\cite{s,kmsy,ttk,ann}.
\footnotesize
\bibliographystyle{plain}
\begin{thebibliography}{10}
\bibitem{s}
S. Saitoh, Generalized inversions of Hadamard and tensor products for matrices, Advances in Linear Algebra \& Matrix Theory. Vol.4 No.2 (2014), 87-95. http://www.scirp.org/journal/ALAMT/
\bibitem{kmsy}
M. Kuroda, H. Michiwaki, S. Saitoh, and M. Yamane,
New meanings of the division by zero and interpretations on $100/0=0$ and on $0/0=0$,
Int. J. Appl. Math. Vol. 27, No 2 (2014), pp. 191-198, DOI: 10.12732/ijam.v27i2.9.
\bibitem{ttk}
S.-E. Takahasi, M. Tsukada and Y. Kobayashi, Classification of continuous fractional binary operators on the real and complex fields, Tokyo Journal of Mathematics (in press).
\bibitem{ann}
Announcement 185: Division by zero is clear as z/0=0 and it is fundamental in mathematics,
Institute of Reproducing Kernels, 2014.10.22.
\end{thebibliography}
\end{document}








0 件のコメント:
コメントを投稿