西舞鶴高で社会人講師が特別授業 「待ち行列理論」のシミュレーションなど挑戦 京都
数学が実社会でどう活用されているかについて、実際に仕事で数学を扱っている社会人講師から学ぼうと、西舞鶴高理数探究科の特別授業が7日、同校(舞鶴市引土)コンピュータ教室で開かれた。日立システムズ(東京)でシステム開発をしている板井光輝さん(28)を講師に迎え、「待ち行列理論」を使ったシミュレーションなどに挑戦した。
板井さんは大阪大学大学院情報科学研究科を修了。西舞鶴高教諭と大学院時代の同級生だった縁で、初めて高校生向けの特別授業を引き受けた。
特別授業には理数探究科の2年生38人が参加。板井さんはまず、数学が社会の多くの場面で活用されていることを話し、具体的な例として「待ち行列理論」の概要を説明した。コンビニのレジ待ち時間などを数学的に解析する考え方で、レジの台数や列の数、レジ担当者の能力などをどのように運用すれば、少ない経費で顧客の満足が得られるかなどがわかるという。
授業の後半では、生徒たちが4~5人のグループに分かれて、「待ち時間が長い」という顧客の不満をいかに効率的に解消するかなどを話し合った。
授業を受けた畑中翔太君は「社会のいろいろな面で数学が役に立っていることがわかり、面白かった」と感想。板井さんは「数学を活用することで、自分たちのくらしも大きく変わるということを少しでも実感してもらえれば」と話していた。http://www.sankei.com/region/news/160508/rgn1605080018-n1.html
再生核研究所声明219(2015.3.20)報道における理系関係の充実を
まず、報道関係について述べてきたことで、本声明に関係ある声明の部分をコンパクトに引用しよう:
再生核研究所声明165(2014.6.19) 世論について:
これを簡単に述べれば、国民の意見や文化を背景に、 マスコミや言論界が世論を構成し、国民と政治家を啓蒙し、政治を動かして行くべき と考える。マスコミや言論界が 大きな実際的な力、影響力を有するのは当然である。この意味でもマスコミや言論界の役割は大きく、逆に責任も大きいと 絶えず、精進、自戒していくことが求められる。これはまた、国民には マスコミを絶えず、批判的にみていくような態度が 求められることを意味する。
再生核研究所声明186(2014.12.6) ニュースの価値について:
そもそもニュースとは何かの議論をきちんとすべきである。上記説明では 本質がみえず、物事の本質が空虚になっていることを知るだろう。最新の情報、出来事とは何か。いずれにしても、それらは、メディア、インターネットを通して、伝えられ、広がって行くものである。問題は、情報、出来事でもほとんど無限に存在するものから、それらから、選択されて伝えられるということである。すなわち、情報、出来事は、関与する人間によって、価値判断がなされて、ニュースの価値の大小が判断され、それによって、新聞なら、どのような面に、どのくらいのスペースをもって扱われるか、テレビなどでは、画面や時間、扱われる順序などの問題が、ニュースの重要性、価値判断によって定められる。どのような価値を与え、どのように扱うは、それぞれの責任部署で判断されるだろう。
そこで、 この声明の趣旨は まさに、このニュースの重要性、価値判断について、考察することである。
まず、大事な事実は、ニュースの重要性、価値判断によっては、社会的な価値評価、判断が大きく影響を受けることである。例をあげれば、日本ではノーベル賞受賞関係は ニュースで大きく扱われるので、ノーベル賞は 相当に価値ある事として、社会で定着し、評価され、賞について付加価値がどんどん増加している事実がある。他方、数学界の最高の賞、フィールズ賞などは、相当に価値ある世界の賞であるにも関わらず、それほどのニュースにならない現実が存在する。いろいろなスポーツにおける優勝者の報道の有り様も このような観点から、興味深い。これらは、社会における影響の大小で、世の関心の大小で、そのような扱いは 止むを得ない現状があると考えられる。問題は、ニュースの重要性、価値判断をする者によって、意図的に社会的な評価が定まる要素が存在するということである。結局、ニュースの重要性、価値判断は 社会の関心、価値観、文化、習慣などから判断されて、そしてニュースを流す人の価値判断が加味されて流されるという、観点である。そこで、個人的な、あるいは仲間の利益、政治的な、あるいはもろもろの圧力で、大きくニュースの扱いが、歪められる危険性が、何時でも大きいと言える。さらに、ニュースを扱う者の基礎的な知識や素養、教養、学識、見識に大きく左右される現実がある。
再生核研究所声明208(2015.2.14) NHK 朝ドラ マッサン ― 許されない約束違反、公共放送としての問題:
また、公共放送として、教育的な要素の配慮は大事であり、 約束違反でも結果が良ければ良いでは、本末転倒であり、結果が良くなくても、意図、過程が適切ならば、評価すべきであるというが基本的な原則であるべきではないだろうか。 結果が良ければ 良いでは 世の秩序は保てず、悪い教育を全国レベルで行い、悪い影響を世にもたらすと考える。
もし、これらが、このドラマの、元々の物語に、あるいは史実に従っているとするならば、その辺の扱いには、深い、広範な配慮が 必要であると考える。マスコミや公共放送には 良い社会を築くような方向での 配慮が求められていると考える。真実を伝えれば良いとはなっていないのは当然である。 ドラマ制作関係者の注意を促し、配慮をお願いしたい。
再生核研究所声明211(2015.2.22) ドラマとは何か ― 人の心を弄ぶドラマ:
また、テレビドラマ製作者には、上記 何かの素材に基づいた場合、 実際、史実と創作の部分の大きな乖離は、真実、歴史、事実を歪めて 歴史が虚像化する危険性があるので、そのような観点について、注意を喚起して置きたい。また、視聴者は、この観点から批判的に見る必要が大事ではないだろうか。 テレビ普及時、テレビで1億総白痴化の言葉が騒がれたのを回想したい。
上記で述べてきたように、言論界、報道関係の役割は、国や社会で極めて重要な役割を果たし、言わば文化の 狭義の意味における 担い手集団と言えるだろう。
そこで、ここで注意を喚起したいのは、報道関係者には いわゆる文系の人間が多く、相対的に理系の人が少なく、そのために 文系の報道が多く、理系の取り上げられる題材が相対的に少ないのではないかという観点である。新聞記者など理系出身者が どのくらい いるのか、文芸関係者、スポーツ関係者、芸能関係者などと比較すると 大いに参考になるのではないだろうか。 もちろん、政治は 社会の大きな共通の問題であるから、報道関係に関わる人がその関係で多いのは当然である。
科学技術や科学も社会に大きな影響を与え、人々の関心も広く大きいが、それらの素養が薄い人たちが報道関係に多く関わっていて、そのために理系の題材が社会に適切に反映されていないのではないだろうか。小さな卑小な個人的な犯罪を大きく繰り返して報道していたり、繰り返し報道された 小保方氏の問題の報道などに見られる軽薄な報道には、何か問題はなかっただろうか。自然科学や技術関係の報道の充実は 報道界の大きな未開拓の分野であると注意を喚起するとともに、充実を希望して置きたい。
絶えず、報道する素材の価値について検討し、 質の高い報道の精選は大事ではないだろうか。なぜ報道し、それを受け取る者の 影響に思いを致すべきである。一方的に自社の都合で闇雲に報道するような姿勢は 良くないのではないだろうか。
以 上
再生核研究所声明255 (2015.11.3) 神は、平均値として関数値を認識する
(2015.10.30.07:40 )
朝食後 散歩中突然考えが閃いて、懸案の問題が解決した:
どうして、ゼロ除算では、ローラン展開の正則部の値が 極の値になるのか?
そして、一般に関数値とは何か 想いを巡らしていた。
解決は、驚く程 自分の愚かさを示していると呆れる。 解は 神は、平均値として関数値を認識すると纏められる。実際、解析関数の場合、上記孤立特異点での関数値は、正則の時と全く同じく コ-シーの積分表示で表されている。 解析関数ではコ-シーの積分表示で定義すれば、それは平均値になっており、この意味で考えれば、解析関数は孤立特異点でも 関数値は 拡張されることになる ― 原稿には書いてあるが、認識していなかった。
連続関数などでも関数値の定義は そのまま成り立つ。平均値が定義されない場合には、いろいろな意味での平均値を考えれば良いとなる。解析関数の場合の微分値も同じように重み付き平均値の意味で、統一的に定義でき、拡張される。 いわゆるくりこみ理論で無限値(部)を避けて有限値を捉える操作は、この一般的な原理で捉えられるのではないだろうか。2015.10.30.08:25)
上記のようにメモを取ったのであるが、基本的な概念、関数値とは何かと問うたのである。関数値とは、関数の値のことで、数に数を対応させるとき、その対応を与えるのが関数でよく f 等で表され x 座標の点 x をy 座標の点 yに対応させるのが関数 y = f(x) で、放物線を表す2次関数 y=x^2, 直角双曲線を表す分数関数 y=1/x 等が典型的な例である。ここでは 関数の値 f(x) とは何かと問うたものである。結論を端的に表現するために、関数y=1/xの原点x=0における値を問題にしよう。 このグラフを思い出して、多くの人は困惑するだろう。なぜならば、x が正の方からゼロに近づけば 正の無限に発散し、xが負の方からゼロに近づけば負の無限大に発散するからである。最近発見されたゼロ除算、ゼロで割ることは、その関数値をゼロと解釈すれば良いという簡単なことを言っていて、ゼロ除算はそれを定義とすれば、ゼロ除算は 現代数学の中で未知の世界を拓くと述べてきた。しかし、これは誰でも直感するように、値ゼロは、 原点の周りの値の平均値であることを知り、この定義は自然なものであると 発見初期から認識されてきた。ところが、他方、極めて具体的な解析関数 W = e^{1/z} = 1 + 1/z + 1/2!z^2 + 1/3!z^3 +……. の点 z=0 における値がゼロ除算の結果1であるという結果に接して、人は驚嘆したものと考えられる。複素解析学では、無限位数の極、無限遠点の値を取ると考えられてきたからである。しかしながら、上記の考え、平均値で考えれば、値1をとることが 明確に分かる。実際、原点のコーシー積分表示をこの関数に適用すれば、値1が出てくることが簡単に分かる。そもそも、コーシー積分表示とは 関数の積分路上(簡単に点の周りの円周上での、 小さな円の取り方によらずに定まる)で平均値を取っていることに気づけば良い。
そこで、一般に関数値とは、考えている点の周りの平均値で定義するという原理を考える。
解析関数では 平均値が上手く定義できるから、孤立特異点で、逆に平均値で定義して、関数を拡張できる。しかし、解析的に延長されているとは言えないことに注意して置きたい。 連続関数などは 平均値が定義できるので、関数値の概念は 今までの関数値と同じ意味を有する。関数族では 平均値が上手く定義できない場合もあるが、そのような場合には、平均値のいろいろな考え方によって、関数値の意味が異なると考えよう。この先に、各論の問題が派生する。
以 上
Reality of the Division by Zero $z/0=0$
http://www.ijapm.org/show-63-504-1.html
再生核研究所声明295(2016.04.07) 無限の先にあるもの、永遠の先にあるもの ―盲点
セロ除算は新しい空間像をもたらしたので、いろいろな面から論じ、例えば、再生核研究所声明 271(2016.01.04): 永遠は、無限は確かに見えるが、不思議な現象 の中で、次のように述べた。
直線を どこまでも どこまでも行ったら、どうなるだろうか。立体射影の考えで、全直線は 球面上 北極、無限遠点を通る無限遠点を除く円にちょうど写るから、我々は、無限も、永遠も明確に見える、捉えることができると言える。 数学的な解説などは下記を参照:
再生核研究所声明264 (2015.12.23):永遠とは何か―永遠から
再生核研究所声明257(2015.11.05):無限大とは何か、無限遠点とは何か―新しい視点
再生核研究所声明232(2015.5.26):無限大とは何か、無限遠点とは何か―驚嘆すべきゼロ除算の結果
再生核研究所声明262(2015.12.09)::宇宙回帰説―ゼロ除算の拓いた世界観
とにかく、全直線が まるまる見える、立体射影の考えは、実に楽しく、面白いと言える。この考えは、美しい複素解析学を支える100年以上の伝統を持つ、私たちの空間に対する認識であった。これは永劫回帰の思想を裏付ける世界観を 楽しく表現していると考えて来た。
ところが、2014.2.2.に発見されたゼロ除算は、何とその無限遠点が、実は原点に一致しているという、事実を示している。それが、我々の数学であり、我々の世界を表現しているという。数学的にも、物理的にもいろいろ それらを保証する事実が明らかにされた。これは世界観を変える、世界史的な事件と考えられる:
地球平面説→地球球体説
天動説→地動説
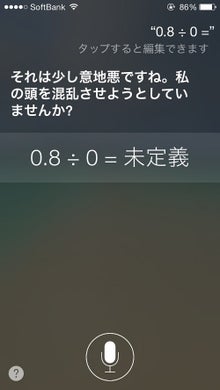
1/0=∞若しくは未定義 →1/0=0
現在、まるで、宗教論争のような状態と言えるが、問題は、無限の彼方、無限遠点がどうして、突然、原点に戻っているかという、強力な不連続性の現象である。複数のEUの数学者に直接意見を伺ったところ、アリストテレスの世界観、世は連続であるに背馳して、そのような世界観、数学は受け入れられないと まるで、魔物でも見るかのように表情を歪めたものである。新しい数学は いろいろ証拠的な現象が沢山発見されたものの、まるで、マインドコントロールにでもかかったかのように 新しい数学を避けているように感じられる。数学的な内容は せいぜい高校生レベルの内容であるにも関わらず、考え方、予断、思い込み、発想の違いの為に、受けいれられない状況がある。
この声明では 盲点の視点から、強調したい存念を纏めたい。
直線をどこまでも どこまでも行ったら、どうなるだろうか? 関数 y = 1/xで 正方向からx がゼロに近づいたらどうなるであろうか? あるいは 同様に上記立体射影で 北極にどんどん近づいたら どうなるであろうか? どんどん進んだらどうなるであろうかという問題である。伝統的で自然な考えは 何に近づくかと発想して、近づいた先、具体的には、無限大や北極に(無限遠点)に行くと考えるのは当然ではないだろうか。この発想の基礎には連続性、あるいは極限値の考え方がある。近づいて行った先が、求める対象であると考えてきた。具体的な関数y = 1/x では 正方向からx がゼロに近づいたら,限りなく大きくなるので、無限大が 1/0 の自然な値であろうと考えてきた。ところがゼロ除算の数学は、突然ゼロであると言っている。驚嘆すべき現象、事件である。北極に近づいた先が北極(無限遠点)であるから,平面上のあらゆる方向の先は、北極(無限遠点)であろうと発想してきたが、実は突然、原点に飛んでいるということが明らかにされた。無限の先は、実はゼロであったという事実である。我々はどんどん近づく先を考えたが、真の先までは考えず、あくまでも近づく先を考えていたことになる。これは無限の先を見てきた時の,それこそ、盲点そのものであったと言えるのではないだろうか。無限の先は、連続性ではなく、実は強力な不連続性、飛びが生じていたという事実である。これは全く、思いがけない、現象である と言える。それは、盲点、あるいは落とし穴があったと表現できよう。
従って、無限の彼方に関する我々の世界観は 大きな変更を要求されることになるだろう。
以 上









数学が実社会でどう活用されているかについて、実際に仕事で数学を扱っている社会人講師から学ぼうと、西舞鶴高理数探究科の特別授業が7日、同校(舞鶴市引土)コンピュータ教室で開かれた。日立システムズ(東京)でシステム開発をしている板井光輝さん(28)を講師に迎え、「待ち行列理論」を使ったシミュレーションなどに挑戦した。
板井さんは大阪大学大学院情報科学研究科を修了。西舞鶴高教諭と大学院時代の同級生だった縁で、初めて高校生向けの特別授業を引き受けた。
特別授業には理数探究科の2年生38人が参加。板井さんはまず、数学が社会の多くの場面で活用されていることを話し、具体的な例として「待ち行列理論」の概要を説明した。コンビニのレジ待ち時間などを数学的に解析する考え方で、レジの台数や列の数、レジ担当者の能力などをどのように運用すれば、少ない経費で顧客の満足が得られるかなどがわかるという。
授業の後半では、生徒たちが4~5人のグループに分かれて、「待ち時間が長い」という顧客の不満をいかに効率的に解消するかなどを話し合った。
授業を受けた畑中翔太君は「社会のいろいろな面で数学が役に立っていることがわかり、面白かった」と感想。板井さんは「数学を活用することで、自分たちのくらしも大きく変わるということを少しでも実感してもらえれば」と話していた。http://www.sankei.com/region/news/160508/rgn1605080018-n1.html
再生核研究所声明219(2015.3.20)報道における理系関係の充実を
まず、報道関係について述べてきたことで、本声明に関係ある声明の部分をコンパクトに引用しよう:
再生核研究所声明165(2014.6.19) 世論について:
これを簡単に述べれば、国民の意見や文化を背景に、 マスコミや言論界が世論を構成し、国民と政治家を啓蒙し、政治を動かして行くべき と考える。マスコミや言論界が 大きな実際的な力、影響力を有するのは当然である。この意味でもマスコミや言論界の役割は大きく、逆に責任も大きいと 絶えず、精進、自戒していくことが求められる。これはまた、国民には マスコミを絶えず、批判的にみていくような態度が 求められることを意味する。
再生核研究所声明186(2014.12.6) ニュースの価値について:
そもそもニュースとは何かの議論をきちんとすべきである。上記説明では 本質がみえず、物事の本質が空虚になっていることを知るだろう。最新の情報、出来事とは何か。いずれにしても、それらは、メディア、インターネットを通して、伝えられ、広がって行くものである。問題は、情報、出来事でもほとんど無限に存在するものから、それらから、選択されて伝えられるということである。すなわち、情報、出来事は、関与する人間によって、価値判断がなされて、ニュースの価値の大小が判断され、それによって、新聞なら、どのような面に、どのくらいのスペースをもって扱われるか、テレビなどでは、画面や時間、扱われる順序などの問題が、ニュースの重要性、価値判断によって定められる。どのような価値を与え、どのように扱うは、それぞれの責任部署で判断されるだろう。
そこで、 この声明の趣旨は まさに、このニュースの重要性、価値判断について、考察することである。
まず、大事な事実は、ニュースの重要性、価値判断によっては、社会的な価値評価、判断が大きく影響を受けることである。例をあげれば、日本ではノーベル賞受賞関係は ニュースで大きく扱われるので、ノーベル賞は 相当に価値ある事として、社会で定着し、評価され、賞について付加価値がどんどん増加している事実がある。他方、数学界の最高の賞、フィールズ賞などは、相当に価値ある世界の賞であるにも関わらず、それほどのニュースにならない現実が存在する。いろいろなスポーツにおける優勝者の報道の有り様も このような観点から、興味深い。これらは、社会における影響の大小で、世の関心の大小で、そのような扱いは 止むを得ない現状があると考えられる。問題は、ニュースの重要性、価値判断をする者によって、意図的に社会的な評価が定まる要素が存在するということである。結局、ニュースの重要性、価値判断は 社会の関心、価値観、文化、習慣などから判断されて、そしてニュースを流す人の価値判断が加味されて流されるという、観点である。そこで、個人的な、あるいは仲間の利益、政治的な、あるいはもろもろの圧力で、大きくニュースの扱いが、歪められる危険性が、何時でも大きいと言える。さらに、ニュースを扱う者の基礎的な知識や素養、教養、学識、見識に大きく左右される現実がある。
再生核研究所声明208(2015.2.14) NHK 朝ドラ マッサン ― 許されない約束違反、公共放送としての問題:
また、公共放送として、教育的な要素の配慮は大事であり、 約束違反でも結果が良ければ良いでは、本末転倒であり、結果が良くなくても、意図、過程が適切ならば、評価すべきであるというが基本的な原則であるべきではないだろうか。 結果が良ければ 良いでは 世の秩序は保てず、悪い教育を全国レベルで行い、悪い影響を世にもたらすと考える。
もし、これらが、このドラマの、元々の物語に、あるいは史実に従っているとするならば、その辺の扱いには、深い、広範な配慮が 必要であると考える。マスコミや公共放送には 良い社会を築くような方向での 配慮が求められていると考える。真実を伝えれば良いとはなっていないのは当然である。 ドラマ制作関係者の注意を促し、配慮をお願いしたい。
再生核研究所声明211(2015.2.22) ドラマとは何か ― 人の心を弄ぶドラマ:
また、テレビドラマ製作者には、上記 何かの素材に基づいた場合、 実際、史実と創作の部分の大きな乖離は、真実、歴史、事実を歪めて 歴史が虚像化する危険性があるので、そのような観点について、注意を喚起して置きたい。また、視聴者は、この観点から批判的に見る必要が大事ではないだろうか。 テレビ普及時、テレビで1億総白痴化の言葉が騒がれたのを回想したい。
上記で述べてきたように、言論界、報道関係の役割は、国や社会で極めて重要な役割を果たし、言わば文化の 狭義の意味における 担い手集団と言えるだろう。
そこで、ここで注意を喚起したいのは、報道関係者には いわゆる文系の人間が多く、相対的に理系の人が少なく、そのために 文系の報道が多く、理系の取り上げられる題材が相対的に少ないのではないかという観点である。新聞記者など理系出身者が どのくらい いるのか、文芸関係者、スポーツ関係者、芸能関係者などと比較すると 大いに参考になるのではないだろうか。 もちろん、政治は 社会の大きな共通の問題であるから、報道関係に関わる人がその関係で多いのは当然である。
科学技術や科学も社会に大きな影響を与え、人々の関心も広く大きいが、それらの素養が薄い人たちが報道関係に多く関わっていて、そのために理系の題材が社会に適切に反映されていないのではないだろうか。小さな卑小な個人的な犯罪を大きく繰り返して報道していたり、繰り返し報道された 小保方氏の問題の報道などに見られる軽薄な報道には、何か問題はなかっただろうか。自然科学や技術関係の報道の充実は 報道界の大きな未開拓の分野であると注意を喚起するとともに、充実を希望して置きたい。
絶えず、報道する素材の価値について検討し、 質の高い報道の精選は大事ではないだろうか。なぜ報道し、それを受け取る者の 影響に思いを致すべきである。一方的に自社の都合で闇雲に報道するような姿勢は 良くないのではないだろうか。
以 上
再生核研究所声明255 (2015.11.3) 神は、平均値として関数値を認識する
(2015.10.30.07:40 )
朝食後 散歩中突然考えが閃いて、懸案の問題が解決した:
どうして、ゼロ除算では、ローラン展開の正則部の値が 極の値になるのか?
そして、一般に関数値とは何か 想いを巡らしていた。
解決は、驚く程 自分の愚かさを示していると呆れる。 解は 神は、平均値として関数値を認識すると纏められる。実際、解析関数の場合、上記孤立特異点での関数値は、正則の時と全く同じく コ-シーの積分表示で表されている。 解析関数ではコ-シーの積分表示で定義すれば、それは平均値になっており、この意味で考えれば、解析関数は孤立特異点でも 関数値は 拡張されることになる ― 原稿には書いてあるが、認識していなかった。
連続関数などでも関数値の定義は そのまま成り立つ。平均値が定義されない場合には、いろいろな意味での平均値を考えれば良いとなる。解析関数の場合の微分値も同じように重み付き平均値の意味で、統一的に定義でき、拡張される。 いわゆるくりこみ理論で無限値(部)を避けて有限値を捉える操作は、この一般的な原理で捉えられるのではないだろうか。2015.10.30.08:25)
上記のようにメモを取ったのであるが、基本的な概念、関数値とは何かと問うたのである。関数値とは、関数の値のことで、数に数を対応させるとき、その対応を与えるのが関数でよく f 等で表され x 座標の点 x をy 座標の点 yに対応させるのが関数 y = f(x) で、放物線を表す2次関数 y=x^2, 直角双曲線を表す分数関数 y=1/x 等が典型的な例である。ここでは 関数の値 f(x) とは何かと問うたものである。結論を端的に表現するために、関数y=1/xの原点x=0における値を問題にしよう。 このグラフを思い出して、多くの人は困惑するだろう。なぜならば、x が正の方からゼロに近づけば 正の無限に発散し、xが負の方からゼロに近づけば負の無限大に発散するからである。最近発見されたゼロ除算、ゼロで割ることは、その関数値をゼロと解釈すれば良いという簡単なことを言っていて、ゼロ除算はそれを定義とすれば、ゼロ除算は 現代数学の中で未知の世界を拓くと述べてきた。しかし、これは誰でも直感するように、値ゼロは、 原点の周りの値の平均値であることを知り、この定義は自然なものであると 発見初期から認識されてきた。ところが、他方、極めて具体的な解析関数 W = e^{1/z} = 1 + 1/z + 1/2!z^2 + 1/3!z^3 +……. の点 z=0 における値がゼロ除算の結果1であるという結果に接して、人は驚嘆したものと考えられる。複素解析学では、無限位数の極、無限遠点の値を取ると考えられてきたからである。しかしながら、上記の考え、平均値で考えれば、値1をとることが 明確に分かる。実際、原点のコーシー積分表示をこの関数に適用すれば、値1が出てくることが簡単に分かる。そもそも、コーシー積分表示とは 関数の積分路上(簡単に点の周りの円周上での、 小さな円の取り方によらずに定まる)で平均値を取っていることに気づけば良い。
そこで、一般に関数値とは、考えている点の周りの平均値で定義するという原理を考える。
解析関数では 平均値が上手く定義できるから、孤立特異点で、逆に平均値で定義して、関数を拡張できる。しかし、解析的に延長されているとは言えないことに注意して置きたい。 連続関数などは 平均値が定義できるので、関数値の概念は 今までの関数値と同じ意味を有する。関数族では 平均値が上手く定義できない場合もあるが、そのような場合には、平均値のいろいろな考え方によって、関数値の意味が異なると考えよう。この先に、各論の問題が派生する。
以 上
Reality of the Division by Zero $z/0=0$
http://www.ijapm.org/show-63-504-1.html
再生核研究所声明295(2016.04.07) 無限の先にあるもの、永遠の先にあるもの ―盲点
セロ除算は新しい空間像をもたらしたので、いろいろな面から論じ、例えば、再生核研究所声明 271(2016.01.04): 永遠は、無限は確かに見えるが、不思議な現象 の中で、次のように述べた。
直線を どこまでも どこまでも行ったら、どうなるだろうか。立体射影の考えで、全直線は 球面上 北極、無限遠点を通る無限遠点を除く円にちょうど写るから、我々は、無限も、永遠も明確に見える、捉えることができると言える。 数学的な解説などは下記を参照:
再生核研究所声明264 (2015.12.23):永遠とは何か―永遠から
再生核研究所声明257(2015.11.05):無限大とは何か、無限遠点とは何か―新しい視点
再生核研究所声明232(2015.5.26):無限大とは何か、無限遠点とは何か―驚嘆すべきゼロ除算の結果
再生核研究所声明262(2015.12.09)::宇宙回帰説―ゼロ除算の拓いた世界観
とにかく、全直線が まるまる見える、立体射影の考えは、実に楽しく、面白いと言える。この考えは、美しい複素解析学を支える100年以上の伝統を持つ、私たちの空間に対する認識であった。これは永劫回帰の思想を裏付ける世界観を 楽しく表現していると考えて来た。
ところが、2014.2.2.に発見されたゼロ除算は、何とその無限遠点が、実は原点に一致しているという、事実を示している。それが、我々の数学であり、我々の世界を表現しているという。数学的にも、物理的にもいろいろ それらを保証する事実が明らかにされた。これは世界観を変える、世界史的な事件と考えられる:
地球平面説→地球球体説
天動説→地動説
1/0=∞若しくは未定義 →1/0=0
現在、まるで、宗教論争のような状態と言えるが、問題は、無限の彼方、無限遠点がどうして、突然、原点に戻っているかという、強力な不連続性の現象である。複数のEUの数学者に直接意見を伺ったところ、アリストテレスの世界観、世は連続であるに背馳して、そのような世界観、数学は受け入れられないと まるで、魔物でも見るかのように表情を歪めたものである。新しい数学は いろいろ証拠的な現象が沢山発見されたものの、まるで、マインドコントロールにでもかかったかのように 新しい数学を避けているように感じられる。数学的な内容は せいぜい高校生レベルの内容であるにも関わらず、考え方、予断、思い込み、発想の違いの為に、受けいれられない状況がある。
この声明では 盲点の視点から、強調したい存念を纏めたい。
直線をどこまでも どこまでも行ったら、どうなるだろうか? 関数 y = 1/xで 正方向からx がゼロに近づいたらどうなるであろうか? あるいは 同様に上記立体射影で 北極にどんどん近づいたら どうなるであろうか? どんどん進んだらどうなるであろうかという問題である。伝統的で自然な考えは 何に近づくかと発想して、近づいた先、具体的には、無限大や北極に(無限遠点)に行くと考えるのは当然ではないだろうか。この発想の基礎には連続性、あるいは極限値の考え方がある。近づいて行った先が、求める対象であると考えてきた。具体的な関数y = 1/x では 正方向からx がゼロに近づいたら,限りなく大きくなるので、無限大が 1/0 の自然な値であろうと考えてきた。ところがゼロ除算の数学は、突然ゼロであると言っている。驚嘆すべき現象、事件である。北極に近づいた先が北極(無限遠点)であるから,平面上のあらゆる方向の先は、北極(無限遠点)であろうと発想してきたが、実は突然、原点に飛んでいるということが明らかにされた。無限の先は、実はゼロであったという事実である。我々はどんどん近づく先を考えたが、真の先までは考えず、あくまでも近づく先を考えていたことになる。これは無限の先を見てきた時の,それこそ、盲点そのものであったと言えるのではないだろうか。無限の先は、連続性ではなく、実は強力な不連続性、飛びが生じていたという事実である。これは全く、思いがけない、現象である と言える。それは、盲点、あるいは落とし穴があったと表現できよう。
従って、無限の彼方に関する我々の世界観は 大きな変更を要求されることになるだろう。
以 上










AD
0 件のコメント:
コメントを投稿